Orbital-engineered anomalous Hall conductivity in stable full Heusler compounds: a pathway to optimized spintronics†
Quynh Anh T.
Nguyen
a,
Thi H.
Ho
 bc,
Seong-Gon
Kim
bc,
Seong-Gon
Kim
 d,
Ashwani
Kumar
e and
Viet Q.
Bui
d,
Ashwani
Kumar
e and
Viet Q.
Bui
 *a
*a
aAdvanced Institute of Science and Technology, The University of Danang, 41 Le Duan, Danang, Vietnam. E-mail: bqviet@ac.udn.vn; mrbuiquocviet@gmail.com
bLaboratory for Computational Physics, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam
cFaculty of Mechanical – Electrical and Computer Engineering, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
dDepartment of Physics & Astronomy and Center for Computational Sciences, Mississippi State University, Mississippi State, Mississippi 39762, USA
eMax-Planck-Institut für Kohlenforschung, 45470 Mülheim an der Ruhr, Germany
First published on 15th August 2024
Abstract
This comprehensive study leverages high-throughput density functional theory (DFT) to systematically explore the electronic, magnetic, and transport properties of 2904 full Heusler compounds, focusing on anomalous Hall conductivity (AHC). The investigation unveils a pronounced influence of the crystallographic phase and valence electron count on material stability and AHC. We report that Heusler compounds, particularly within the L21 phase and with 20 to 30 valence electrons, exhibit superior stability and AHC. Notably, Rh2MnGa and Co2MnAl emerge as exemplary, with AHCs of 1847 S cm−1 and 1646 S cm−1, respectively, vastly outperforming traditional ferromagnets like Fe, Co, and Ni. The detailed electronic structure analysis of Co2MnAl reveals a half-metallic character, crucial for high spin polarization and AHC, underscored by prominent Co–Co and Co–Mn hybridization. Furthermore, the study sheds light on the significant role of spin–orbit coupling in enhancing AHC through the modulation of band splitting and Berry curvature. The findings not only expand the understanding of Heusler compounds but also offer guidance in designing materials with tailored AHC for next-generation spintronic applications.
Introduction
Spintronics is an emerging field in information technology that combines three conventional information carriers: electron charge, spin, and photon.1,2 These carriers represent the three important essential foundations of information technology: data processing with electron transport, data storage with an assembly of spins, and data transfer through optical connections. With the recent rapid advancements in information technology, there is a growing demand for both larger data-storage capacity and faster data processing. This can be achieved through the scaling of physical dimensions for enhanced speed, while maintaining power density by voltage scaling. Nevertheless, the optimization of these factors continues to be a difficult task.3,4 This is because further reduction of the supply voltage could lead to an exponential increase in the leakage current. As a result, this not only negatively impacts the performance of the spintronic devices but also poses significant reliability issues.Recent explorations into novel materials for fabricating next-generation electronic devices have attracted great attention.3,5 Among the materials investigated, Heusler compounds are particularly notable in spintronics research due to their rich electronic and magnetic properties.6–11 Full Heusler compounds are one of the main types of Heusler compounds. They have the chemical formula X2YZ, where X and Y are transition metals and Z is an s–p element. With various possible combinations of X, Y and Z, the electronic structure and magnetic properties can be tuned as desired.2 Recently, the application of full-Heusler compounds as multifunctional materials, including metals,12 half-metals,13 superconductors,14 and topological insulators15 with ferromagnetic and ferrimagnetic behaviors has been reported.16,17 Furthermore, these compounds are renowned for their high Curie temperature18,19 and substantial anomalous and spin Hall conductivity,20,21 making them ideal for spintronic devices operating at room temperature.
The anomalous Hall effect (AHE) in ferromagnets has attracted considerable attention for investigations of electronic transport characteristics. This effect offers a straightforward way to examine the spin polarization of carriers, a crucial factor in the advancement of spintronic devices.22,23 In half-metallic systems such as Heusler compounds, the AHE is very useful for probing spin–orbit coupling (SOC). This examination of SOC is crucial for understanding the influences of SOC on the evolution of the band structure and atomic order in relation to the growth parameters of the materials.22 Karplus and Luttinger introduced the concept of anomalous velocity, which is understood as the curvature of the Berry phase in momentum space, providing a theoretical framework to explain the AHE in ferromagnetic materials.24,25 Recently, the AHE has been extensively investigated in magnetic Heusler compounds through anomalous Hall conductivity (AHC).20–22,26–30 Shubhankar Roy et al.26 reported the essential role of spin–orbit coupling and its influence on the electronic band structure as well as the magnitude and direction of AHC. Yimin Ji et al.21 performed high-throughput principles calculations to obtain the AHC of Heusler compounds, indicating the AHC is determined not just by the number of valence electrons or atomic weights, but rather by the specific characteristics of the electronic structures. Therefore, the AHC studies will reveal patterns and provide strategic insights for engineering materials with tailored properties for spintronic applications.
Herein, we employed high-throughput density functional theory (DFT) calculations to explore and predict the AHE of 2904 full-Heusler compounds. Our work has identified compounds with remarkable AHC values, such as Rh2MnGa, which exhibits an AHC of 1847 S cm−1 and a magnetic moment of 4.07μB, highlighting its exceptional stability and potential for spintronic applications. Similarly, Co2MnAl with an AHC of 1646 S cm−1 and a robust magnetic moment of 4.14μB, along with Ti2PtSn and Mn2TiAl with significant AHCs of 1319 and 1267 S cm−1, respectively, showcases the versatility of Heusler compounds for technological applications. This extensive dataset spans a broad spectrum of elemental substitutions within the Heusler structure, facilitating a systematic assessment of how compositional variations influence the AHE. Our approach not only encompasses the calculations of AHC but also delves into the detailed investigation of the electronic structures and magnetic stability of these compounds.
The relevance of this study lies in the unveiling of novel Heusler compounds with significant AHE potential, poised to play a vital role in the advancement of next-generation spintronic devices. By comprehensively understanding the interplay between the electronic structure and AHE, we are paving the way for the development of materials with tailored properties, optimal for specific applications in magnetic storage and spin-based electronics. The findings from our work significantly contribute to the growing database of Heusler compounds with characterized electronic and magnetic properties, thereby propelling further research and technological innovations in the dynamic field of spintronics.
Computational details
Our computational investigation into the electronic structures and AHC of full-Heusler compounds utilizes the spin-polarized density functional theory as implemented in the Vienna Ab initio Simulation Package (VASP).31–33 Within this framework, the projector augmented-wave (PAW) method serves as the foundation for our calculations.34 The exchange–correlation effects are approximated by generalized gradient approximation (GGA), precisely following the Perdew–Burke–Ernzerhof (PBE) formalism,35 which has been rigorously tested for the reliable portrayal of electronic properties in a diverse array of materials. A careful selection of computational parameters ensures the accuracy of our results: we employ an energy cutoff of 400 eV for plane-wave basis set expansion to guarantee the precise representation of electronic wavefunctions. Brillouin zone sampling is accomplished with a dense Monkhorst–Pack k-mesh of 15 × 15 × 15, chosen to strike a balance between computational efficiency and the resolution necessary for accurate electronic structure determination. The convergence of energy between successive self-consistent field iterations is stringently controlled to within 10−6 eV, ensuring that the calculated properties reflect a true ground state. Further delving into the electronic structure, we construct maximally localized Wannier functions (MLWFs) from the computed Bloch states via the Wannier90 package.36 This approach facilitates the quantification of the intrinsic contributions to AHC, enabling us to dissect the complex interplay between band topology and transport phenomena in these compounds.For each configuration of Heusler compounds, our computational strategy involves generating 18 maximally localized Wannier functions (MLWFs) for the transition metal atoms X and Y, and 8 MLWFs for the Z atom from the Bloch states. This is approximately twice the number of MLWFs generally utilized, chosen to enhance the precision of our electronic structure representation. The initial projections of the Bloch states for X and Y atoms are chosen as a hybridization of s, p, and d orbitals, specifically sp3d2, and for Z atoms as sp3. To ensure the accurate disentanglement of bands and generation of MLWFs, the upper limit of the energy window is set to 5.0 eV above the Fermi level (EF). For the construction of the MLWFs, we employed a dense k-mesh of 4 × 4 × 4.
The intrinsic contribution to anomalous Hall conductivity (AHC) is quantified through the Kubo formula, which is mathematically expressed as follows:37
 | (1) |
 | (2) |
By applying these rigorous computational techniques, we ensure a comprehensive understanding of the dependency of the AHC on the electronic structure, which is crucial for tailoring materials to meet the specific needs of spintronic technology.
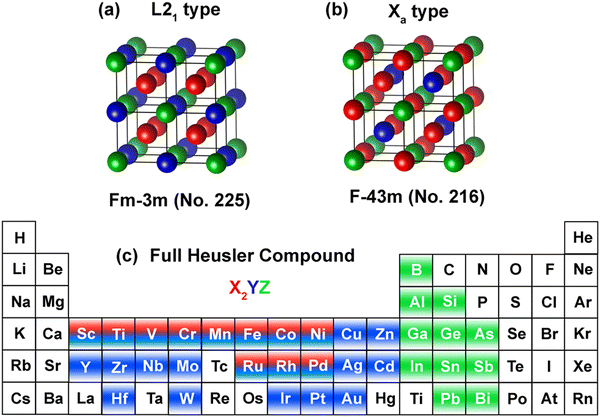
For the structural construction of the full cubic Heusler compounds under consideration, we focused on the two most prevalent crystallographic phases: the regular L21 and the inverse Xa. The L21 phase, illustrated in Fig. 1(a), is characterized by cubic symmetry within the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SG 225), where transition metals occupy the X and Y positions (depicted in blue and green, respectively) and the main group elements are denoted by Z (illustrated in red). In this configuration, the X atoms are positioned at the 8c Wyckoff sites (¼, ¼, ¼), Y atoms at the 4b sites (½, ½, ½), and Z atoms at the 4a sites (0, 0, 0). Conversely, the inverse Xa structure, shown in Fig. 1(b) and associated with the space group F
m (SG 225), where transition metals occupy the X and Y positions (depicted in blue and green, respectively) and the main group elements are denoted by Z (illustrated in red). In this configuration, the X atoms are positioned at the 8c Wyckoff sites (¼, ¼, ¼), Y atoms at the 4b sites (½, ½, ½), and Z atoms at the 4a sites (0, 0, 0). Conversely, the inverse Xa structure, shown in Fig. 1(b) and associated with the space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (SG 216), presents a unique arrangement where the X transition-metal atoms have a lower valence compared to the Y transition-metal atoms.
3m (SG 216), presents a unique arrangement where the X transition-metal atoms have a lower valence compared to the Y transition-metal atoms.
The exploration comprised 2904 potential structures, each derived from a diverse palette of elements occupying the X, Y, and Z positions as delineated in the periodic table of Fig. 1(c). For geometrical optimization, we fully relaxed the unit cells, permitting atomic positions to be refined until reaching an energy convergence threshold of less than 10−5 eV for the optimization steps. This meticulous optimization process ensures that the computed properties are reflective of the lowest energy structures, a prerequisite for accurate predictions of physical behaviors such as AHC and magnetic stability.
Formation energy is used to explore the structural stability of Heusler compounds, calculated using the following formula:
 | (3) |
Results and discussion
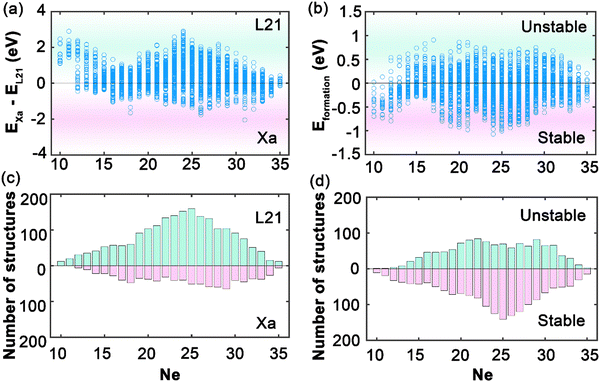
In this study, we have conducted a thorough investigation of the stability and electronic structures across an expansive set of 2904 full Heusler compounds, with an aim to deepen the understanding of their potential in advanced applications. Fig. 2 illustrates the initial segment of our findings, portraying the intricate energy profiles that dictate the phase stability and hence the usability of these materials within nanotechnological domains, such as spintronics. In Fig. 2(a), the energy difference as a function of the total number of total valence electrons (Ne) between the L21 and Xa structures is elucidated; negative values indicate that the Xa structure is energetically more favorable, whereas positive values denote a predominance of the L21 structure, especially notable as Ne increases. Aggregation according to Ne in Fig. 2(c) reveals a distinct peak at Ne equal to 25, within a range concentrated between 20 and 30 Ne, indicating a marked preference for the stability of L21 structures in this electronic configuration. The Xa structures exhibit a more even distribution, suggesting a less pronounced dependency on Ne. Fig. 2(b) presents the formation energies, with negative values signifying stability, dominating the assembly of compounds; this stability profile is reflected in Fig. 2(d), which, when compiled by Ne, displays a trend analogous to the L21 and Xa structural distribution. The analysis delineates that Heusler compounds exhibit a predilection for stability within the L21 phase, particularly for combinations of X, Y, and Z resulting in a total Ne within the 20–30 range. This not only identifies a domain of structural stability but also highlights an optimal region for engineering materials with the desired electronic configurations for spintronic applications, laying a vital foundation for the development of materials with properties tailored for the progression of advanced technological applications.Fig. 3 illustrates the AHC as a function of the total valence electron Ne in full Heusler compounds. This behavior is categorized into three distinctive regions which correlate closely with the Slater–Pauling rule38,39 for total magnetic moment: 10 ≤ Ne ≤ 16, 16 ≤ Ne ≤ 25, and Ne ≥ 25. Such correlation suggests that AHC is intimately linked with the magnetic properties of these materials, adhering to the foundational magnetic behavior predicted using the Slater–Pauling curve. The first region, where 10 ≤ Ne ≤ 16, is characterized by a progressive increase in AHC, peaking sharply at Ne = 14. Here, we observe the highest AHC values corresponding to compounds with X constituents such as Sc and Ti. This suggests that, in this range, the compounds with early transition metals are more likely to exhibit enhanced Hall conductivity, which can be attributed to their lower d-band occupancy allowing for a higher degree of spin polarization as per the Slater–Pauling curve. In the intermediate region of 16 ≤ Ne ≤ 25, AHC demonstrates a similar pattern, climbing to its apex at Ne = 21, then gradually declining. The compounds yielding high AHC in this segment predominantly have X constituents like Mn and Fe. This can be rationalized by considering the increased d-band filling for these elements, leading to more complex band interactions and potentially higher magnetic moments that favor substantial AHC values as they approach the saturation of the d-band just before Ne reaches 24. The final region, Ne ≥ 25, where AHC is shown to be maximal at Ne = 28, corresponds to elements with X constituents like Fe, Ru, Co, and Rh. The high AHC values in this range could be linked to the closeness to full d-band occupancy, which would be expected to reduce the magnetic moment as per the Slater–Pauling behavior. These trends across the different regions reflect the Slater–Pauling behavior where the AHC intensifies, reaches a maximum, and then tapers, mirroring the corresponding magnetic phenomena. The pronounced peaks in AHC within specific Ne ranges suggest that optimal electronic structures exist for maximizing Hall conductivity. This insight opens avenues for strategically engineering Heusler compounds with enhanced magnetic and electronic transport properties, tailored for spintronic applications. The data thus provide a roadmap for the compositional tuning of Heusler compounds to harness their full potential in advanced technological applications, particularly in devices that leverage spintronic phenomena.
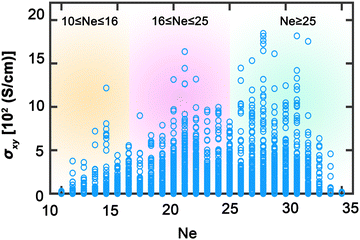 | ||
| Fig. 3 Anomalous Hall conductivity σxy as a function of total valence electron Ne. Yellow, purple, and cyan backgrounds distinguish three areas: 10 ≤ Ne ≤ 16, 16 ≤ Ne ≤ 25, and Ne ≥ 25, respectively. | ||
Additionally, Table 1 elucidates the remarkable magnitude of AHC within an array of Heusler compounds, juxtaposed against their stability and magnetic characteristics. Our calculated ΔF shows good agreement with the open quantum materials dataset.40 All cases show positive hull distance ΔH, except for Rh2MnAl with ΔH = 0, which means that the material is thermodynamically stable. This reveals that select compounds, notably Rh2MnGa and Co2MnAl, exhibit not only formidable stability, indicated by their negative formation energies, but also AHC values of 1847 and 1646 S cm−1, respectively. These figures significantly surpass traditional AHCs of elemental ferromagnets such as Fe, Co, and Ni.41–43 Overall, our calculated AHC exhibits similar tendency and order of magnitude to previously reported values, especially with 19 ≤ Ne ≤ 33.44 The observed increase in the AHC is directly linked to the distinctive electronic structure of Heusler compounds. Their adaptive alloying capability enables extensive modulation of magnetic and transport properties. A deliberate selection of elements X, Y, and Z leads to electronic configurations that yield high magnetic moments, which in turn is manifest in elevated AHC values. This correlation underscores the profound impact of targeted elemental synthesis on the emergent physical properties of these compounds, as demonstrated in our findings. The data clearly show that enhancements in AHC result from strategic element selection within the Heusler framework, a crucial factor for achieving exceptional AHC. This is vital for advancing spintronics, particularly in applications that require precise spin current detection and efficient magnetic switching.
| X2YZ | Stable phase | ΔF (eV per atom) | ΔH (eV per atom) | |σxy| (S cm−1) | M tot (μB) | P (%) | |αxy| (A K−1 T−1) |
|---|---|---|---|---|---|---|---|
| a Theoretical data.40 b Theoretical data.44 c Theoretical data.46 d Experimental data.47 e Experimental data.45 f Theoretical data.48 g Theoretical data.49 h Theoretical data.50 i Theoretical data.51 j Theoretical data.52 | |||||||
| Rh2MnGa | l21 | −0.569 | 0.000a | 1847 | 4.07 | 93 | 1.55 |
| −0.537a | 1862b | 4.10b | 3.82b | ||||
| 4.05c | |||||||
| Co2MnAl | l21 | −0.385 | 0.009a | 1646 | 4.14 | 63 | 2.62 |
| −0.356a | 1631b | 4.04b | 68f | 1.93b | |||
| 1600d | 4.01e | 75g | |||||
| Ti2PtSn | l21 | −0.429 | 0.260a | 1319 | 1.79 | 48 | 3.29 |
| −0.487a | |||||||
| Mn2TiAl | l21 | −0.397 | 0.002a | 1267 | 3.01 | 81 | 1.81 |
| −0.344a | 1128b | 2.98h | 82h | 1.03b | |||
| Ru2WSi | l21 | −0.020 | 0.308a | 1036 | 1.24 | 34 | 2.99 |
| −0.03a | |||||||
| Sc2CrSb | l21 | −0.167 | 0.422a | 899 | 2.88 | 17 | 4.68 |
| −0.167a | 3.16i | ||||||
| V2IrAl | x a | −0.480 | 0.093a | 869 | 1.60 | 70 | 2.29 |
| −0.472a | |||||||
| Cr2IrGe | x a | −0.067 | 0.138a | 826 | 0.97 | 97 | 0.04 |
| −0.072a | |||||||
| Fe2MnGa | l21 | −0.024 | 0.042a | 717 | 2.14 | 66 | 5.85 |
| −0.014a | 454b | 2.02j | 74j | ||||
| Ni2RhAl | x a | −0.408 | 0.124a | 513 | 0.84 | 75 | 5.54 |
| −0.425a | |||||||
To explore this further, we performed a detailed correlation analysis between AHC and the total magnetic moment (Mtot) for the compounds listed in Table 1, observing a moderately strong linear correlation with an R2 value of 0.663 (Fig. S1(a), ESI†). However, extending this analysis to the entire database reveals a more complex relationship, with a wide range of AHC values for the same Mtot, as shown in Fig. S1(b) (ESI†). Thus, this complexity necessitates considering additional factors such as the total valence electron count (Ne), which follows the Slater–Pauling rule. Indeed, plots of AHC and Mtot as a function of Ne (Fig. S1(c) and (d), ESI†) reveal similar behavior, delineating three regions: 10 ≤ Ne ≤ 16, 16 ≤ Ne ≤ 25, and Ne ≥ 25. Additionally, we have calculated the spin polarization for each of the full Heusler compounds listed in Table 1 using the formula 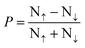 , where N↑ and N↓ are the densities of states for the up and down spin channels, respectively. The spin polarization values, which range from 17% to 97%, highlight the significant variation in electronic configurations across different compounds (Fig. S2, ESI†). High spin polarization indicates a high degree of spin polarization at the EF, which is beneficial for spintronic applications. To facilitate comparison, we have included additional theoretical and experimental data in Table 1. The Co2YZ Heusler compounds have been extensively studied both theoretically and experimentally due to their outstanding reputation in the field. Consequently, we have also provided the properties of the Co2MnZ family in Table S1 (ESI†). Our calculated values for the Mtot and P align closely with other computational and experimental results.
, where N↑ and N↓ are the densities of states for the up and down spin channels, respectively. The spin polarization values, which range from 17% to 97%, highlight the significant variation in electronic configurations across different compounds (Fig. S2, ESI†). High spin polarization indicates a high degree of spin polarization at the EF, which is beneficial for spintronic applications. To facilitate comparison, we have included additional theoretical and experimental data in Table 1. The Co2YZ Heusler compounds have been extensively studied both theoretically and experimentally due to their outstanding reputation in the field. Consequently, we have also provided the properties of the Co2MnZ family in Table S1 (ESI†). Our calculated values for the Mtot and P align closely with other computational and experimental results.
To further explore the factors influencing the AHC in Heusler compounds, we analyzed the relationship between AHC and the valence electron, as well as the electronegativity differences between the constituent elements. Fig. S3 (ESI†) presents the AHC as a function of the valence electrons for X, Y, and Z elements and the valence electron differences between them. ΔXY, ΔXZ, and ΔYZ denote valence electron differences between X and Y, X and Z, and Y and Z, respectively. The largest AHC values for X elements occur at valence electrons of 7 and 9, while for Y elements, the highest AHC is observed at 7, 9, and 10 valence electrons. For Z elements, the distribution of AHC is relatively uniform across different valence electrons. Additionally, Fig. S3 (ESI†) shows that significant AHC values for ΔXY are observed in the ranges −2 ≤ ΔXY ≤ 0 and ΔXY ≈ 2, for ΔXZ at 4 and 6, and for ΔYZ at 4, 6, and 7. Furthermore, Fig. S4 (ESI†) shows the AHC as a function of electronegativity for X, Y, and Z elements and the electronegativity differences between them (ΔXY, ΔXZ, ΔYZ). These analyses reveal that both valence electron and electronegativity differences play crucial roles in determining the AHC. For instance, the highest AHC values are observed for X elements with electronegativity values of approximately 1.8 and 2.3, for Y elements at around 1.6 and 2.2, and for Z elements uniformly across the studied range. The differences in electronegativity that yield high AHC values are concentrated around −0.4, 0, and 0.7 for ΔXZ, and −0.4 ≤ ΔXZ ≤ 0.7. Furthermore, high AHC values are observed around −0.3 ≤ ΔYZ ≤ −0.1, and ΔYZ ≈ −0.5 and 0.5. These results highlight the importance of considering both the valence electron count and electronegativity in the design of Heusler compounds with optimized AHC properties.
We also provide the anomalous Nernst conductivity (ANC), closely related to the anomalous Hall effect, is a phenomenon in which a current is induced by a temperature gradient. In this study, we calculated the ANC using the formula53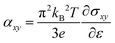 , where kB is the Boltzmann constant, T is the temperature, and ∂ε = 0.01 eV is the energy interval. Fig. S5 (ESI†) shows ANC as a function of chemical potential μ for selected compounds: Rh2MnGa, Co2MnAl, Ti2PtSn, Mn2TiAl, Ru2WSi, Sc2CrSb, V2IrAl, Cr2IrGe, Fe2MnGa, and Ni2RhAl. ANC exhibits significant sensitivity to variations in the EF, similar to AHC. For instance, in Mn2TiAl and Fe2MnGa, a high slope of AHC near EF results in a pronounced ANC. As the temperature increases, ANC also increases, highlighting the interplay between thermal effects and the electronic structure. The specific values of ANC at EF for T = 300 K are included in Table 1.
, where kB is the Boltzmann constant, T is the temperature, and ∂ε = 0.01 eV is the energy interval. Fig. S5 (ESI†) shows ANC as a function of chemical potential μ for selected compounds: Rh2MnGa, Co2MnAl, Ti2PtSn, Mn2TiAl, Ru2WSi, Sc2CrSb, V2IrAl, Cr2IrGe, Fe2MnGa, and Ni2RhAl. ANC exhibits significant sensitivity to variations in the EF, similar to AHC. For instance, in Mn2TiAl and Fe2MnGa, a high slope of AHC near EF results in a pronounced ANC. As the temperature increases, ANC also increases, highlighting the interplay between thermal effects and the electronic structure. The specific values of ANC at EF for T = 300 K are included in Table 1.
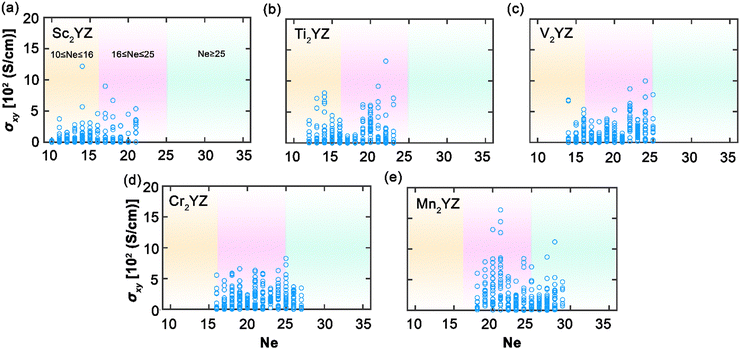
Fig. 4 presents a nuanced view of AHC across Heusler compounds, categorized by the transition metal element X when X is less than half-filled. It is evident that the distribution of AHC largely skews toward Ne values less than 25, with the notable exception of Mn-based compounds, reflecting a strong dependence on the specific electronic configuration of the transition metal element. For Sc-based compounds, the highest AHC is observed at Ne = 14, which is suggestive of the fewer d-electrons in Sc facilitating higher spin polarization and resultant Hall conductivity. Ti compounds follow a distinct pattern, peaking at Ne = 22, which may reflect the more complex d-orbital interactions as Ti approaches half-filling. The high AHC for Mn at Ne = 21 underscores its robust magnetic character among the transition metals, likely contributing to its pronounced Hall effect. Notably, the AHC for V- and Cr-containing compounds remains relatively consistent across the studied Ne range, possibly indicating a more stable electronic structure that is less sensitive to the variation in the number of valence electrons. The relatively lower AHC values for these elements compared to Sc and Ti suggest that their closer proximity to half-filling results in less pronounced spin polarization effects conducive to AHC. As a half-filled transition metal, Mn demonstrates larger AHC values affirming the strong link between magnetic properties and AHC. This correlation is consistent with the established understanding that magnetic moments and spin–orbit coupling are significant contributors to AHC in such materials. The data from Fig. 4, therefore, not only provide insight into the electronic structure-dependent behavior of AHC in Heusler compounds but also point to the potential of specific elemental configurations, particularly those involving Mn, in achieving high AHC values suitable for spintronic applications.
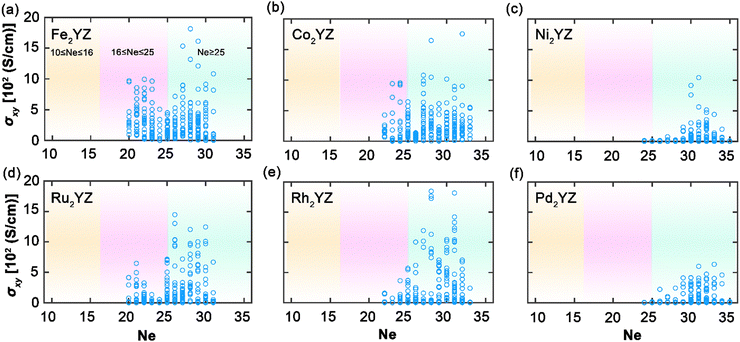
Extending our analysis to Fig. 5, we examine the distribution of AHC for Heusler compounds where X element is more than half-filled. The data primarily cover Ne values greater than 20, indicating that these compounds generally exhibit higher AHCs compared to those with X elements that are less than half-filled, as shown in Fig. 4. The AHC values within this group, particularly for Fe-, Co-, Ru-, and Rh-based compounds, are notably higher, which is in line with their position in the periodic table, alluding to their similar valence electron counts. This similarity results in comparable electronic structures that facilitate high AHC, with the largest values for Fe appearing between Ne values of 27 and 29 and for Co at Ne = 22, likely due to their proximity to full d-band occupancy which promotes enhanced spin polarization. In contrast, Ni and Pd, both near or at full d-band filling, show reduced AHC values. The diminished AHC can be attributed to poorer d-orbital hybridization, as full filling leads to a lower number of available states for conduction, thus reducing the probability of spin-dependent scattering essential for a large AHC. This trend is particularly interesting as it reflects the sensitivity of AHC to the specific electronic configuration and hybridization of d-orbitals in Heusler compounds. The insights obtained here underscore the nuanced interplay between electron filling, magnetic properties, and resultant AHC. Understanding this relationship is vital for the tailored design of Heusler compounds with high AHC for spintronic applications, where maximizing spin-dependent transport phenomena is crucial.
Delving deeper into the electronic structure, Fig. 6 presents the band structures for Co2MnAl, segregated into spin-up and spin-down channels, which sheds light on the intrinsic properties leading to its high AHC. This compound, which is ferromagnetic, aligns with the Slater–Pauling rule manifesting a total magnetic moment close to 4μB, with individual contributions of 0.77μB from Co and 2.7μB from Mn for a total valence electron count of 28. Our results show good agreement with previous studies.44,45 The band structure of Co2MnAl reveals a half-metallic character, with the spin-up channel exhibiting metallic behavior, with bands almost fully occupied near the EF. Conversely, the spin-down channel acts as a semiconductor, displaying a direct gap at the Γ point of 0.46 eV. This gap is pivotal as it suggests high spin polarization at EF, which is a desirable trait for spintronic applications due to its potential to facilitate spin current without charge current. The contribution of Al to AHC is negligible since its states are distributed far from EF. In contrast, the states of Co are closer to EF, with smaller exchange splitting compared to Mn, implying that the contribution of Co to the total AHC is less than that of Mn. At the Γ point, hybridization between the states of Co leads to a bandgap opening, further illustrating the complex interaction between elements and the collective impact on the electronic properties of the material. Analyzing this band structure is fundamental in understanding the underlying mechanisms that govern the AHC in Co2MnAl. It is the intricate hybridization of the Co and Mn states and the resultant energy band dispersion that underpins the substantial AHC observed. The calculations performed for Co2MnAl not only confirm its high AHC but also provide a concrete example of how electronic band structure details are paramount in evaluating and predicting material properties for advanced spintronic devices.
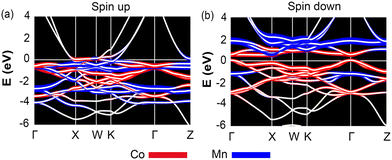 | ||
| Fig. 6 Band structure of Co2MnAl for (a) spin-up and (b) spin-down channels. Red and blue denote the contributions of Co and Mn, respectively. | ||
Fig. 7 provides a compelling visualization of the band structure and Berry curvature for Co2MnAl, a ferromagnetic Heusler compound, in both spin channels after including the SOC. The bands are color-coded from blue (representing spin −ℏ/2) to red (representing spin +ℏ/2), clearly indicating that most bands are well split by SZ, highlighting the significant influence of SOC. The band structure (Fig. 7a) exhibits the profound effect of SOC, as spin is not a good quantum number in its presence, leading to bands that are non-degenerate in most parts of the k-space. The band splitting, which is particularly evident along high-symmetry lines, is a key factor in determining the AHC of the material. In Fig. 7b, the total Berry curvature Ωxy along the same high-symmetry lines reflects a general prevalence of Ω > 0 over Ω < 0, contributing to a sizeable total AHC of 1646 S cm−1, which is in good agreement with both experimental and theoretical reports.44,46 Notably, the distribution of the Berry curvature shows two dominant positive peaks at 1/3XW and near K, while smaller peaks appear along GX, WK, and FZ. The negative Berry curvature is less prevalent, with a single significant peak along KG. The AHC as a function of chemical potential μ (Fig. 7c), within the same energy range as the band structure, peaks at the EF. This maximum in AHC corresponds to the maximal spin polarization between the spin-up and spin-down channels and is predominantly contributed by the Co–Co hybridization. The spectrum of this large peak in AHC ranges from approximately −0.8 to 1 eV, indicating that the regions of high Co–Co and Co–Mn hybridization contribute significantly to AHC. Outside this energy range, the AHC values diminish. The detailed analysis of Fig. 7 hence underlines the critical role of SOC and the resultant band splitting in enhancing the AHC in Co2MnAl. These insights into the spin-resolved electronic structure and the distribution of the Berry curvature across the Brillouin zone are essential for understanding the mechanisms driving the high AHC in this compound, affirming its suitability for spintronic applications where high spin-polarization and efficient spin-current generation and manipulation are desired.
Conclusion
In conclusion, this extensive study on full Heusler compounds using high-throughput DFT calculations has uncovered remarkable insights into their electronic, magnetic, and transport properties, particularly their AHC. Our systematic investigation into over 2904 compounds has revealed that both the crystal structure and the electron count play critical roles in determining the stability and the AHC of these materials. Key findings from our research highlight that Heusler compounds with a total valence electron count (Ne) between 20 and 30 exhibit enhanced stability within the L21 phase, as evidenced by compounds such as Rh2MnGa, which demonstrates an AHC of 1847 S cm−1 and a magnetic moment of 4.07μB, and Co2MnAl, with an AHC of 1646 S cm−1 and a magnetic moment of 4.14μB. These values are notably superior to those of elemental ferromagnets like Fe, Co, and Ni, underscoring the potential of Heusler compounds in transcending the performance of conventional magnetic materials.Our focused examination of Co2MnAl revealed a half-metallic nature, which is instrumental in achieving high spin polarization and, consequently, a high AHC. The intricate interplay between Co–Co and Co–Mn hybridization within this specific compound has been shown to contribute significantly to the observed AHC, which peaks in the vicinity of the Fermi level. Moreover, the study elucidates the crucial role of SOC in the band structure of Heusler compounds. SOC not only influences band splitting but also substantially affects the Berry curvature distribution, which directly impacts AHC. The presented results not only contribute to the fundamental understanding of the intrinsic properties of Heusler compounds but also serve as a guide for the design of new materials with high AHC for advanced spintronic applications. By delineating the correlation between AHC and the intrinsic magnetic and electronic properties of the materials, we pave the way for the strategic synthesis of Heusler compounds with customized properties for specific technological applications.
Our research thus concludes with significant implications for the field of spintronics, providing a solid foundation for the future exploration of novel magnetic materials with high AHC, targeting applications that range from spin current detection to magnetic switching in state-of-the-art devices.
Author contributions
Viet Q. Bui supervised the research and wrote the original manuscript. Quynh Anh T. Nguyen and Thi H. Ho performed the DFT calculations. All authors participated in revising the manuscript.Data availability
The data supporting the findings of this study are available within the article and the ESI.† Additional data, including computational codes and raw data files generated during the study, are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was financially supported by the Vietnam Ministry of Education and Training (code: B2023.DNA.11). We also thank the US DOE INCITE program and National Science Foundation ACCESS program for providing the computing resources.References
- A. Hirohata and K. Takanashi, J. Phys. D: Appl. Phys., 2014, 47, 193001 CrossRef.
- P. Barla, V. K. Joshi and S. Bhat, J. Comput. Electron., 2021, 20, 805–837 CrossRef CAS.
- E. C. Ahn, npj 2D Mater. Appl., 2020, 4, 17 CrossRef CAS.
- B. Dieny, I. L. Prejbeanu, K. Garello, P. Gambardella, P. Freitas, R. Lehndorff, W. Raberg, U. Ebels, S. O. Demokritov, J. Akerman, A. Deac, P. Pirro, C. Adelmann, A. Anane, A. V. Chumak, A. Hirohata, S. Mangin, S. O. Valenzuela, M. C. Onbaşlı, M. d’Aquino, G. Prenat, G. Finocchio, L. Lopez-Diaz, R. Chantrell, O. Chubykalo-Fesenko and P. Bortolotti, Nat. Electron., 2020, 3, 446–459 CrossRef.
- Y. Liu, C. Zeng, J. Zhong, J. Ding, Z. M. Wang and Z. Liu, Nano-Micro Lett., 2020, 12, 93 CrossRef CAS PubMed.
- K. Elphick, W. Frost, M. Samiepour, T. Kubota, K. Takanashi, H. Sukegawa, S. Mitani and A. Hirohata, Sci. Technol. Adv. Mater., 2021, 22, 235–271 CrossRef CAS PubMed.
- C. J. Palmstrøm, Prog. Cryst. Growth Charact. Mater., 2016, 62, 371–397 CrossRef.
- L. Bainsla and K. G. Suresh, Appl. Phys. Rev., 2016, 3, 031101 Search PubMed.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- F. Claudia and H. Burkard, J. Phys. D: Appl. Phys., 2007, 40, E01 Search PubMed.
- S. Chatterjee, S. Chatterjee, S. Giri and S. Majumdar, J. Condens. Matter Phys., 2022, 34, 013001 CrossRef CAS PubMed.
- S. E. Kulkova, S. V. Eremeev, T. Kakeshita and S. S. Kulkov, Mater. Trans., 2006, 47, 599–606 CrossRef CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429 CrossRef.
- K. Ramesh Kumar, V. Chunchu and A. Thamizhavel, J. Appl. Phys., 2013, 113, 17E155 CrossRef.
- A. Amirabadizadeh, S. A. Abbas Emami, Z. Nourbakhsh, S. M. Alavi Sadr and S. M. Baizaee, J. Supercond. Novel Magn., 2017, 30, 1035–1049 CrossRef CAS.
- I. Galanakis and E. Şaşıoğlu, Appl. Phys. Lett., 2011, 99, 052509 CrossRef.
- A. K. Nayak, M. Nicklas, S. Chadov, P. Khuntia, C. Shekhar, A. Kalache, M. Baenitz, Y. Skourski, V. K. Guduru, A. Puri, U. Zeitler, J. M. D. Coey and C. Felser, Nat. Mater., 2015, 14, 679–684 CrossRef CAS PubMed.
- S. Kc, R. Mahat, S. Regmi, J. Y. Law, V. Franco, G. Mankey, W. H. Butler, A. Gupta and P. LeClair, Acta Mater., 2022, 236, 118112 CrossRef CAS.
- R. Chellakumar, T. S. D. Malar, A. N. Rawther and K. Ravichandran, J. Supercond. Novel Magn., 2023, 36, 547–557 CrossRef CAS.
- M. F. Tanzim, N. Fortunato, I. Samathrakis, R. Xie, I. Opahle, O. Gutfleisch and H. Zhang, Adv. Funct. Mater., 2023, 33, 2214967 CrossRef CAS.
- Y. Ji, W. Zhang, H. Zhang and W. Zhang, New J. Phys., 2022, 24, 053027 CrossRef CAS.
- S. Husain, A. Kumar, S. Akansel, P. Svedlindh and S. Chaudhary, J. Magn. Magn. Mater., 2017, 442, 288–294 CrossRef CAS.
- N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539–1592 CrossRef.
- R. Karplus and J. M. Luttinger, Phys. Rev., 1954, 95, 1154–1160 CrossRef.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1997, 392, 45–57 Search PubMed.
- S. Roy, R. Singha, A. Ghosh, A. Pariari and P. Mandal, Phys. Rev. B, 2020, 102, 085147 CrossRef CAS.
- J. Kudrnovský, V. Drchal and I. Turek, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014422 CrossRef.
- M. Blinov, A. Aryal, S. Pandey, I. Dubenko, S. Talapatra, V. Prudnikov, E. Lähderanta, S. Stadler, V. Buchelnikov, V. Sokolovskiy, M. Zagrebin, A. Granovsky and N. Ali, Phys. Rev. B, 2020, 101, 094423 CrossRef CAS.
- G. Xing, K. Masuda, T. Tadano and Y. Miura, Acta Mater., 2024, 270, 119856 CrossRef CAS.
- H.-L. Huang, J.-C. Tung and G.-Y. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 134409 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse, J. Non-Cryst. Solids, 1995, 192–193, 222–229 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune, J. Ibañez-Azpiroz, H. Lee, J.-M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi and J. R. Yates, J. Condens. Matter Phys., 2020, 32, 165902 CrossRef CAS PubMed.
- G.-Y. Guo, S. Murakami, T.-W. Chen and N. Nagaosa, Intrinsic Spin Hall Effect in Platinum: First-Principles Calculations, Phys. Rev. Lett., 2008, 100(9), 096401 CrossRef CAS PubMed.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429 CrossRef.
- J. Kubler, Phys. B+C, 1984, 127, 257 Search PubMed.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 1 Search PubMed.
- X. Wang, J. R. Yates, I. Souza and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195118 CrossRef.
- X. Wang, D. Vanderbilt, J. R. Yates and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195109 CrossRef.
- H. R. Fuh and G. Y. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 144427 CrossRef.
- J. Noky, Y. Zhang, J. Gooth, C. Felser and Y. Sun, npj Comput. Mater., 2020, 6, 77 CrossRef CAS.
- P. Webster, J. Phys. Chem. Solids, 1971, 32, 1221 CrossRef CAS.
- I. Galanakis, P. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429 CrossRef.
- E. Vilanova Vidal, G. Stryganyuk, H. Schneider, C. Felser and G. Jakob, Appl. Phys. Lett., 2011, 99, 132509 CrossRef.
- J.-C. Tung and G.-Y. Guo, New J. Phys., 2013, 15, 033014 CrossRef CAS.
- J. Kübler and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 012405 CrossRef.
- M. Meinert, J.-M. Schmalhorst and G. Reiss, J. Condens. Matter Phys., 2010, 23, 036001 CrossRef PubMed.
- Y. Han, Z. Chen, M. Kuang, Z. Liu, X. Wang and X. Wang, Res. Phys., 2019, 12, 435 Search PubMed.
- Y. Kudryavtsev, N. Uvarov, V. Iermolenko, I. Glavatskyy and J. Dubowik, Acta Mater., 2012, 60, 4780 CrossRef CAS.
- D. Xiao, Y. Yao, Z. Fang and Q. Niu, Phys. Rev. Lett., 2006, 97, 026603 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information on the complete database, which includes 2904 structures. See DOI: https://doi.org/10.1039/d4tc02116a |
| This journal is © The Royal Society of Chemistry 2024 |