Open Access Article
Open Access ArticleEfficiency in photocatalytic production of hydrogen: energetic and sustainability implications
Rocío
Sayago-Carro†
 ,
Luis José
Jiménez-Chavarriga†
,
Esperanza
Fernández-García†
,
Anna
Kubacka
* and
Marcos
Fernández-García
,
Luis José
Jiménez-Chavarriga†
,
Esperanza
Fernández-García†
,
Anna
Kubacka
* and
Marcos
Fernández-García
 *
*
Instituto de Catálisis y Petroleoquímica, CSIC, C/Marie Curie, 2, 28049 Madrid, Spain. E-mail: ak@icp.csic.es; mfg@icp.csic.es
First published on 2nd September 2024
Abstract
Hydrogen generation through a photocatalytic process appears to be a promising technology to produce this energy vector through a novel, efficient, green, and sustainable process. The fruitful use of sunlight as an excitation source and renewable bio-derived reactants as well as the development of highly efficient catalysts are required to achieve this goal. In this perspective article, we focus on describing how to braid energy and sustainability sides of hydrogen photo-generation into a single parameter, allowing quantitative measurement and trustful comparison of different catalytic systems. Starting from the energy-related efficiency parameters defined by the IUPAC, we present novel approaches leading to parameters enclosing energy and sustainability information. The study is completed with the analysis of other, non-IUPAC, parameters of broad use such as the solar-to-hydrogen observable. The set of results available in the literature for the water splitting reaction and the use of bio-derived sacrificial molecules are reviewed to assess the potential of such reactions in the energy-efficient and sustainable production of hydrogen.
1. Introduction
Hydrogen is a key molecule in many chemical industry processes related to the production of fuels, commodity molecules, and high added value chemicals through hydrogenation reactions and others, and appears as a new energy vector with implications in many new fields including transportation, household and industrial processes. The use of this molecule in such a broad number of chemical processes would be supported by its good properties, in one way or another related to the relatively wide availability on earth due to its huge abundance in terms of mass concerning other elements, its high reactivity and reasonable energy storage capability, as well as the fact that energy release can take place without generating harmful products to the environment or humans. Catalysis and, particularly, photocatalysis can play a role in the hydrogen economy, working on both sides of production and consumption, as part of green and environmentally respectful processes.1,2Photocatalysis uses light to trigger a significant number of chemical reactions and can profit from the use of sunlight as a natural and renewable energy source.3–5 The setting up of true green processes for hydrogen generation not only requires a renewable energy source but also renewable reactants. Water is a paradigmatic case but if seawater cannot be directly utilized, the massive use of this molecule to produce hydrogen would be detrimental for other uses and hydrogen photo-production would thus compete with water supply for human and agriculture related needs. Also, another critical aspect concerns the physical separation of hydrogen and oxygen, ideally carried out concomitantly with their production, to achieve affordable or competitive cost when compared with the nowadays dominant production from methane reforming and/or the electrolysis of water.6,7 Alternative molecules generated from bio-based processes can be also good candidates for the massive production of hydrogen. Fermentation derived biomolecules, typically alcohols but also blend with other molecules (like the ABE mixture, e.g. acetone, butanol and ethanol), would be thus desirable candidates in the quest of producing renewable hydrogen.8–11
A key aspect common to all photocatalytic processes and thus for those aiming to produce hydrogen is the bottleneck derived from the efficiency of the processes.3–5 Although increasing the always limited efficiency of photocatalytic processes is a must, a previous, seminal question concerns how to define, measure and interpret efficiency. Efficiency is primarily an energy-related parameter associated with any chemical process but a full understanding of the efficiency of a photocatalytic reaction requires including chemical information with implications on sustainability. As a case study, the analysis of the efficiency of the production of hydrogen from alcohols and, generally speaking, carbon-containing molecules, should take into account the evolution of such molecules and the corresponding carbon-containing products generated during reaction. The (carbon-based) product selectivity would have energy-related implications, in this case mainly although not exclusively connected with the consumption of charge carrier species and, in turn, photons during the reaction. Of course, a global understanding of energy related issues requires a full knowledge of the thermodynamics and kinetics of the reaction. On the other hand, as will be shown below, sustainability issues can be connected with the atom selectivity to the target product, in this case hydrogen, as often several hydrogen-containing molecules are produced in the reaction, with the exception of the splitting of water reaction. Other relevant issues for photocatalytic hydrogen production would be connected with environmental and economic issues, also primarily affected by the products generated during the reaction. Although we would not consider in detail these last two due to their limited relationship with the efficiency parameter, it can be noted that the production of hydrogen from waste or the co-production of hydrogen and carbon-containing value added products are research fields with significance in relation to the just mentioned environmental or economic aspects of the process.5,8
By analyzing the new perspectives available in the literature, here we will carry out a complete study of the key energy and sustainability related aspects of the reaction in connection with the efficiency of the process. This would provide a holistic view of the measurement and interpretation of the mentioned parameter. In this context, we would note that a survey of literature results suggest, as a first impression, that a rigorous measurement of the efficiency of a light related catalytic process is significantly more complex than that in thermal or classical counterparts. Moreover, there is relatively little information that can allow a real comparison of the performance of photocatalysts coming from different studies. Both facts are intimately linked with the analysis of the light distribution at the reaction medium for any photoreactor configuration as well as for any photocatalytic reaction, and thus for hydrogen production. Measuring and modeling light intensity at a reactor can be carried out at different levels of accuracy mostly as a result of the complex nature of the experimental measurement as well as the computational effort required to achieve an error below experimental uncertainly in the spectral/spatial/directional description of the intensity of light.12,13 Despite that, the literature presents several parameters that can provide different levels of understanding of the efficiency of a photocatalytic process.14,15 In fact, a myriad of parameters attempt to measure efficiency, and here we will analyze systematically the most significant ones. The way they are defined and the corresponding experimental/modelling tools required can classify them in a simple way. As outlined above, some of them require the measurement of experimental observables, but in some cases, they also require the above mentioned modeling of the light distribution in the reaction. Rather than showing the mathematical part of the study, the pros and cons as well as the quality of the information extracted from the most representative efficiency parameters for the photocatalytic production of hydrogen will be discussed here. The holistic view attempts to facilitate the progress of the field and to set up the conditions to promote the quantitative measurement of activity in the photocatalytic production of hydrogen and, by extension, for any photocatalytic reaction.
2. Efficiency: energy and sustainability
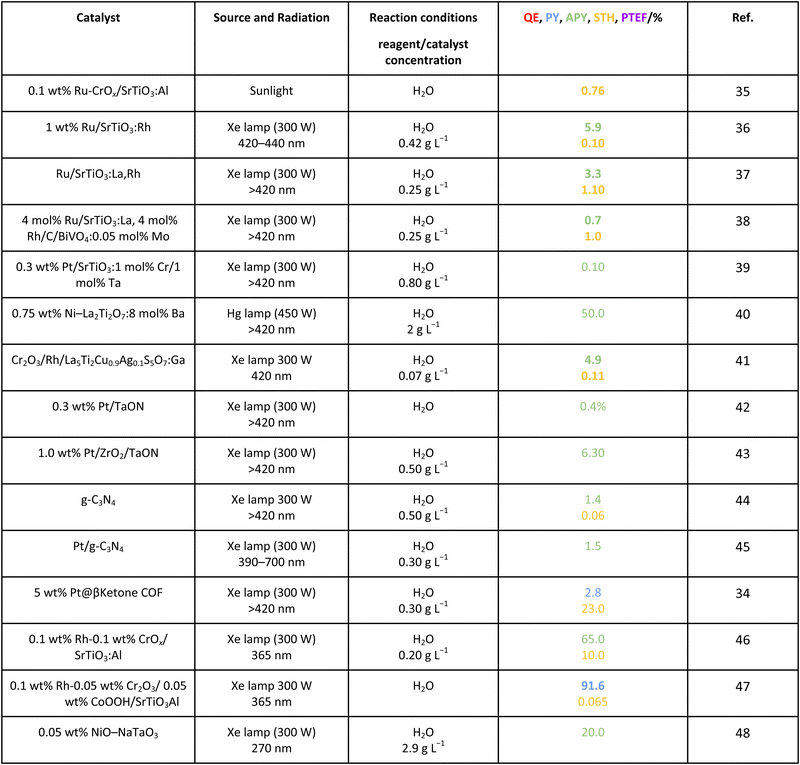
As efficiency is primarily an energy related parameter, a basic definition comes out from IUPAC recommendations and common sense. Efficiency is described as the ratio between the input and output energy of the reaction, measured joule-to-joule. In photocatalysis, this parameter is dependent on the number of photons, the source of the energy, per unit time (the rate of energy production) involved in the reaction.16 Work carried out in recent years attempts to provide parameters rendering the real or approximate estimations of efficiency.13,14,17Table 1 summarizes the general formulation of the efficiency in photocatalytic measurements as well as some simple parameters attempting to provide alternative (and more feasible or practical) formulations. A few of the calculations are specific and display wide application within the (sub)field of hydrogen production. Note that Table 1 collects parameters expressed as a fraction (of unity), although parallel formulations can be presented in percentage (×100).| Parameter | Ref. |
|---|---|
| Efficiency: IUPAC definition | 16 |
| η = energy output/energy input | |
| Global efficiency of the process | 13, 14, 16 and 17 |
| η = ηSourceηreactorηreaction | |
| η Source = radiant energy (rate of photon generation)/energy input | |
| η reactor = rate of photon inside the reactor/rate of photon generation | |
| η reaction = ηAbsηϕ | |
| η Abs = rate of photon absorption/rate of photon inside the reactor | |
| η ϕ = rate of the target molecule/rate of photon absorption | |
| STH: solar to hydrogen | 18–20 |
| STH = [rate of the target molecule (mol s−1) × 237 × 103 (J mol−1)/P (W m−2) × A (m−2)] | |
| PTEF: photochemical thermodynamic efficiency factor | 21 and 22 |
| PTEF = [rate of the primary radical produced (OH•)/rate of photon absorption] | |
2.1. Global efficiency
The global efficiency of a photoreaction reaction (second row of Table 1) can be defined conceptually as composed of three different terms. Each term can have an associated parameter. They define the different parts of the process to extract a rational interpretation of the losses taking place and thus to provide a complete answer to the interpretation of the efficiency. A first point to note is that some of these parameters can be calculated or approximated by a single parameter and, as said, can be estimated using different degrees of approximation.The first term of the global efficiency is ηSource. If the energy source is the sun, we can consider that this parameter would take the unit value although the analysis of the “efficiency” in collecting sunlight at a reactor using parabolic or other concentrators would provide a different value.23 If an artificial source is utilized, the efficiency is always below 1 and depends primarily on the type of lamp. Obviously, LED lamps would have higher efficiency than mercury or xenon lamps as they have lower heat losses. Complete information about how to calculate this factor using artificial sources within the context of a photocatalytic process can be found in ref. 24–28.
The second term concerns the reactor under illumination, ηreactor. Sometimes it is called the reactor radiation incidence efficiency. Measuring (experimentally) the photons at each point of a reactor cannot be accounted for under most experimental conditions as the light-measurement equipment will interfere with light, cannot be physically allocated at the reactor, and/or the corresponding measurement cannot achieve adequate spatial discrimination. Moreover, if the dispersion of light is a relevant contribution to the mater–light interaction process, light intensity at any point of a reactor is intimately associated with the catalyst presence at the reaction medium. In brief, from a practical point of view, this term corresponds to a loss term mainly associated with the radiation losses taking place through all the walls of the reactor. On occasions, the coupling of ηreactor × ηAbs is the one calculated and reported. For some of the IUPAC definitions, such as the photonic yield, the experimental measurement of light intensity, or more properly, the number of photons per unit time, behind the illuminated reactor wall/window(s) is required.16 So, not all radiation losses will be accounted for while using the IUPAC defined parameter. The light intensity after the corresponding wall/window (the one illuminated) is, on the other hand, a boundary condition included in the calculation of the last term presented in the global efficiency, ηreaction.12,13 As it is obvious, ηreactor cannot achieve a unity value. The corresponding value depends primarily on the geometry of illumination and reactor configuration but also on catalyst concentration and physico-chemical properties.
Most of the literature concerns the calculation of the ηreaction term. As the central piece of the formulation, this term contains the calculation of the so-called “quantum efficiency” of the process, ηϕ. Rigorously, the parameter requires measurement/calculation of the rate of reaction and the rate of photon absorption. The difficulty in providing an accurate value for the last parameter leads to different ways of calculation as well as the use of alternative parameters substituting it. In this context, we stress the fact that illumination in a photocatalytic reactor is carried out using multi-wavelength sources. This is the case of sunlight and also of artificial light sources with reasonable light intensity. Other valuable experiments with relatively poor control of hydrodynamic conditions (using reaction chambers rather than reactors) and/or model conditions can use monochromatic, laser-type sources. The multi-wavelength nature of the source of interest defines the way the quantum efficiency parameter is calculated in photocatalysis and here utilized. Nevertheless, parallel definitions are available for efficiency parameters measuring ηreaction for monochromatic light sources.16
So, through the need of obtaining the rate of photon absorption, the rigorous calculation of the quantum efficiency requires careful measurement of the boundary conditions using actinometry and/or radiometry and the use of numerical procedures to obtain the intensity of light at each point of the reactor. The rate of photon absorption is the product of the absorption coefficient of the catalyst multiplied by the intensity of light at each point of the reactor. The interaction of light with matter in a photocatalytic reactor defines two types of systems. The first one is called pseudo-homogeneous and typically corresponds to suspended solids. Dispersion of light plays a key role although is not the single light–matter effect of relevance as absorption, reflection and refraction of light should be considered. Three methods are the most popular to obtain the rate of photon absorption through the solving of the integro-differential radiative transfer equation. These are the discrete ordinate method, the finite volume method and the Monte Carlo method. They are exact as far as true convergence is obtained in the spectral/spatial/directional representation of light at the reactor. As they all imply intensive computational effort, more simple methods taking advantage of a limited representation(s) of the directional properties of light at the reactor or other simplifications have been implemented. These methods facilitate the solving of the integro-differential radiative transfer equation through the use of (semi-) closed (analytical) formulae instead of the use of numerical (accurate) tools.12,13,29 New methods recently proposed in the literature used machine learning and literature results to set up alternative procedures to calculate ηreaction without detailed analysis of the light–matter interaction taking place under reaction conditions. They provide an alternative way of measuring ηreaction to the one presented in Table 1, although the results show that similar observables as the rate of photon absorption should be utilized in order to provide meaningful results.30 The second type of system is called heterogeneous and the main light–matter events are absorption/transmittance, reflection and refraction. They mostly relate to supported catalysts although some systems specifically designed for multiple scattering (like photonic materials) would not be considered “heterogeneous”. In any case, here the relevant optical properties of the solids and the rate of photon absorption are obtained with the help of experimental measurements of the above mentioned optical properties and boundary conditions and the application of classical optics.12,13,23
As will be shown hereafter, for hydrogen photo-production, water splitting reports display relatively low values (except for tests using monochromatic sources) of the efficiency parameters. Higher values are typically encountered for the production of hydrogen using sacrificial molecules. In any case, realistic calculations would lead to a value below 0.3–0.2 in the best cases. Considering that ηSource could be considered unity for the best case but ηreactor has inherent losses for all configurations reported and thus a value below unity, the maximum (true) efficiency reported would never exceed 0.3 or 30%. This appears to be a reasonable upper bound limit. Values reported above this point would suffer from severe simplifications, in most cases associated with the analysis of the relevant properties of the illumination source. These typically concern (i) the handling of the total photon flux of the light source as monochromatic (using a central wavenumber which, even using filters, is incorrect); (ii) the use of the nominal power of the source or a simple evaluation of the radiation field intensity; and/or (iii) restriction of the radiation–catalyst interaction model to absorption events.
For our purposes, a critical issue, connected with the (not so obvious) relationship in the sustainability of the chemical process, comes out from the dimensionality of the quantum efficiency parameter as defined in Table 1. The physical units of the parameter are mole of the target molecule per mole (Einstein) of photons. To provide a dimensionless efficiency parameter, the so-called “selectivity” factor should be included in the denominator of ηϕ. The new efficiency parameter is called the fraction of useful photons, ηΘ. Such a parameter uses the selectivity factor 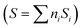 that can be calculated as the summation (calculated, i, on the basis of the molecule utilized to measure the reaction rate present at the numerator of the efficiency parameter, in our case, hydrogen) over all products of the reaction of the inverse of the number of charge carrier species (ni) involved in the generation of the product multiplied by its fractional selectivity (Si). Considering that one photon is used to generate one (electron–hole) charge carrier pair, the units of the selectivity factor are mole of the target molecule per Einstein of photons.13 Through the selectivity factor, the inclusion of chemical information in the quantum efficiency parameter leads to a new dimensionless parameter that allows measuring the real fraction of the (initial) photons involved in the reaction. It takes into account the fact that the different products of a reaction consume a different number of charge carrier species and in turn photons. This is easily visualized considering that the oxidation or the reduction of a chemical species can progress with the formation of different products. For example, in the case of a sacrificial molecule utilized for hydrogen production, the oxidation of the molecule would progress up to carbon dioxide through several intermediates usually containing a higher proportion of oxygen than the initial molecule. As shown later in this work, as there is a univocal correlation between the number of charge carrier species and the production of hydrogen, the fraction of useful photons also provides the ground for a measure of the sustainability of the reaction through the relationship with the atom efficiency on a hydrogen basis.
that can be calculated as the summation (calculated, i, on the basis of the molecule utilized to measure the reaction rate present at the numerator of the efficiency parameter, in our case, hydrogen) over all products of the reaction of the inverse of the number of charge carrier species (ni) involved in the generation of the product multiplied by its fractional selectivity (Si). Considering that one photon is used to generate one (electron–hole) charge carrier pair, the units of the selectivity factor are mole of the target molecule per Einstein of photons.13 Through the selectivity factor, the inclusion of chemical information in the quantum efficiency parameter leads to a new dimensionless parameter that allows measuring the real fraction of the (initial) photons involved in the reaction. It takes into account the fact that the different products of a reaction consume a different number of charge carrier species and in turn photons. This is easily visualized considering that the oxidation or the reduction of a chemical species can progress with the formation of different products. For example, in the case of a sacrificial molecule utilized for hydrogen production, the oxidation of the molecule would progress up to carbon dioxide through several intermediates usually containing a higher proportion of oxygen than the initial molecule. As shown later in this work, as there is a univocal correlation between the number of charge carrier species and the production of hydrogen, the fraction of useful photons also provides the ground for a measure of the sustainability of the reaction through the relationship with the atom efficiency on a hydrogen basis.
2.2. Other parameters
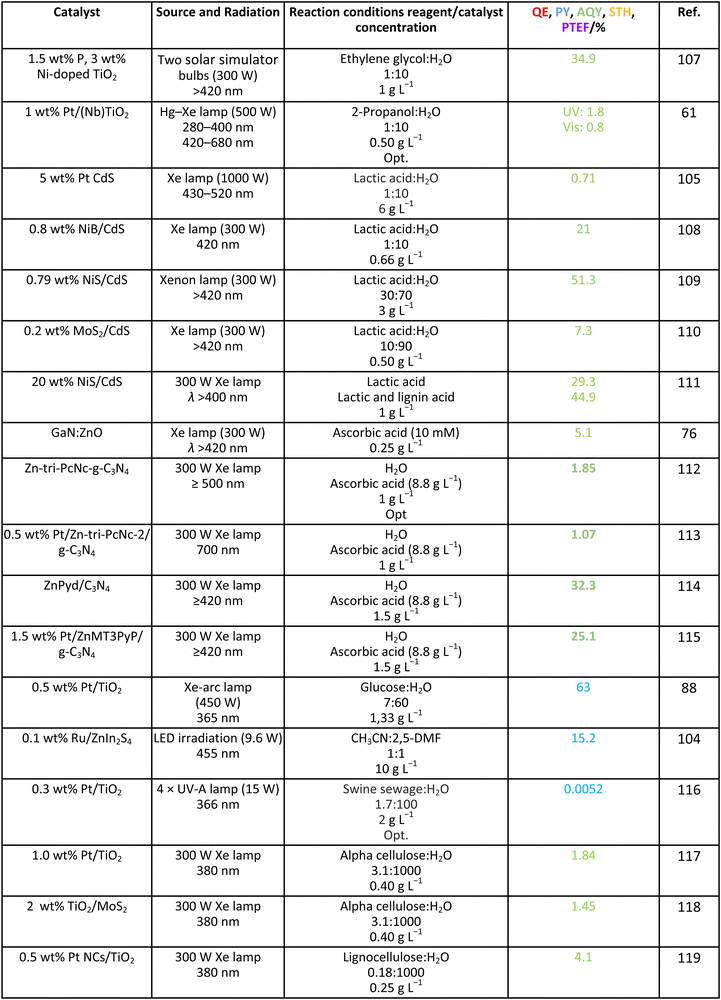
A second point to mention in the context of analyzing ηϕ is the formulation of alternative parameters that would be easier to obtain and would substitute the quantum efficiency parameter. For polychromatic sources, the IUPAC defines the so-called “quantum yield” for this purpose. As mentioned, such a definition eliminates the calculation of the rate of photon absorption in ηϕ and utilizes the rate of incident photons inside the irradiated window of the reactor.16 So, instead of using the absorbed photons, the quantum yield uses the impinging photons once the reactor losses are considered in a first approximation (radiation losses inherent to the illuminated but not all walls of the reactor). A trivial inspection of Table 1 indicates that this parameter would not allow obtaining a meaningful value for the (global) efficiency, η, of the process but can serve as a guide to estimate ηreaction. As trivially deduced from its definition, the photonic yield renders a lower bound to the accurate calculation (e.g. using the quantum efficiency) of ηreaction. Note however that a significant number of reports do not use the IUPAC definition(s) to report efficiency and typically use the total incident photon flux (instead of the rate of photon absorption or the photon flux inside the irradiated window) to provide a different parameter, commonly called “apparent quantum efficiency” or by the IUPAC “apparent (photonic) yield”. This parameter, not included in Table 1, is obsolete according to the IUPAC. Nevertheless, due to its broad use, we will collect information in the following section(s) using such parameters.16In the way to provide simple estimations of the efficiency and thus to avoid the complex experimental-modeling methodologies required for accurate estimation, other simple parameters have been implemented by several authors. The most popular by far is the so-called solar-to-hydrogen STH parameter. The parameter measures the chemical energy of the hydrogen produced vs. the incident sunlight energy. The incident energy is referenced to the Air Mass 1.5 Global (AM 1.5G; 100 mW cm−2) standard. Although initially developed for (photo)electrochemical methods, the application of STH as collected in Table 1 has been utilized by many authors in the photocatalysis field.18–20 STH is a parameter originally designed for the pure water splitting reaction, but the literature shows its use for reactions utilizing sacrificial agents. The maximum value would depend on the solar range (source) to be used. If the UV/visible/IR component is the target source, the maximum of the parameter is around ca. 3.3/43/53%. Of course, the sun provides IR photons at sea level up to ca. 2500 nm (in fact, up to 1800 nm as CO2/water essentially absorbs all photons above such cut-off), but no single material is able to use (relatively) low energy photons. Likely, the harvesting of nearIR photons up to the cut-off energy just mentioned would require the participation of carbonaceous-type materials and/or lanthanides with engineering f-electron subshells. These options appear to be able to profit from the solar spectrum up to a wavelength of ca. 1150 nm (1.08 eV). An additional option for the future could be the use of double-photon technologies but nowadays these are rather inefficient and typically utilize rather toxic and/or unstable (under reaction conditions) materials.31 From the above discussion, a target value of 10% requires the use of the visible and/or the nearIR contributions of sunlight and, if the profit is limited to ca. 1150 nm, top values above 65–70% are unattainable. Such a maximum does not consider any type of loss and thus is an upper bound.
Considering the interpretation of the STH observable, a key point, repeatedly mentioned in the literature, is that the useful range of the solar spectrum utilized in the photocatalytic process depends primarily on the band gap energy of the catalyst and there is no direct or straightforward way of introducing such information into the STH parameter. In fact, the STH parameter is a kind of black box, as the losses cannot be associated with confidence with any physical parameter of the reactor or the reaction (including the photocatalyst) that would allow the optimization of the process. As mentioned before, the adequate measure of the effects of light absorption under reaction conditions can be only achieved through the rate of photon absorption or equivalent formulations and, in general, the full knowledge of the ηSourceηreactorηreaction efficiencies is required. Nevertheless, the strongest point of the STH parameter comes out from the relatively easy calculation of the maximum achievable for a specific material (primarily defined by the band gap energy) as well as its wide application. Valuable tests for different reactor configurations and semiconductors with different band gap energies covering the UV, visible and nearIR ranges have been presented in the literature.32,33
As a representative example of other useful parameters of relatively limited application for measuring efficiency in hydrogen production, we can present the so-called “photochemical thermodynamic efficiency” factor. Table 1 shows that this parameter replaces, in the formulae of the quantum efficiency, the rate of target molecule production by the rate of formation of the primary radical involved (for our purposes, hydrogen production, hydroxyl type radicals). The parameter will thus provide a way to measure the ratio of the energy consumed in the reaction vs. the input energy. Depending on the path for hydroxyl generation, the maximum PTEF achieved can be different. In the absence of oxygen, hydroxyl radicals can be formed exclusively from holes and a unity value appears as the maximum value. In the presence of oxygen, the maximum value can be up to 1.3.21,22
3. Production of hydrogen: efficiency
Once the different efficiency parameters were presented and their interpretation discussed, we will review the literature data. To this end, we will present data corresponding to water splitting as well as the reforming type reactions taking place with the help of most frequently used sacrificial agents such as alcohols, acids, sugars and others. Some reports provide information concerning several sacrificial molecules and are considered separately for each case included in the study. The summary of the literature attempts to illustrate the dual (energy but also sustainability related) information enclosed in the studies reported. This implies that the perspective article focuses attention on two types of studies. First, we selected works carrying out the analysis of light intensity at the reactor to report the IUPAC recommended parameters and/or the analysis of efficiency parameters presented in Table 1. Second, other works are selected as they provide a complete report about the selectivity of the reaction when sacrificial agents are used. Although the set of results presented may not provide a complete view of the field of the photocatalytic production of hydrogen, it is ideally suited to sustain the analysis of the efficiency of the reaction in terms of energy and sustainability issues. In this context, we note that full information about the different catalyst formulations and characteristics is available in many review articles, such as those described in the introduction section.3,4,6,8–11For each “type of” substrate (water, carbon-containing molecules) mentioned, we summarize the relevant information in two tables enclosing the information of the efficiency and, when required and/or available, the selectivity of the reaction. Concerning the efficiency, we summarize results considering five–six different parameters encountered in the literature. Here such results are defined in terms of the mathematical process utilized rather than the efficiency parameters claimed to be calculated by the authors. These are the (i) quantum efficiency (QE) and (ii) photonic yield (PY) parameters reported in publications following the IUPAC recipes, as discussed in the previous section. Connected with the QE parameter we also investigated (iii) the fraction of useful photons. We also summarized data considering (iv) the apparent (photonic) yield (APY), calculated using the incident photon flux in the denominator of the efficiency parameter. As mentioned in the previous section, this is frequently called by certain authors as apparent quantum efficiency. Finally, the (v) solar-to-hydrogen (STH) and (vi) photochemical thermodynamic efficiency factor (PTEP) parameters are presented as defined in Table 1. A general point is that most of the quantum efficiency, photonic yield or apparent photonic yield data are calculated using a factor 2 multiplying the reaction rate. Although the authors may not be aware, this constant is the selectivity factor for the photocatalytic generation of hydrogen. Thus, in the case of quantum efficiency, the reported parameter is, in fact, the dimensionless “fraction of useful photons”. In the other four parameters, the introduction of this factor is relatively meaningless although may find ground through the parallelism with the quantum efficiency. We will further discuss these points and their implications in subsequent paragraphs. Finally, a summary of the relevant information for the most studied reactions is depicted in an associated figure. This figure attempts to summarize the information of charge carrier species as well as the evolution of the reactants under reaction conditions. With the complete picture of the process, we would have the basis to rationalize the literature results reporting the efficiency of the photocatalytic process in terms of energy and sustainability issues.
3.1. Water
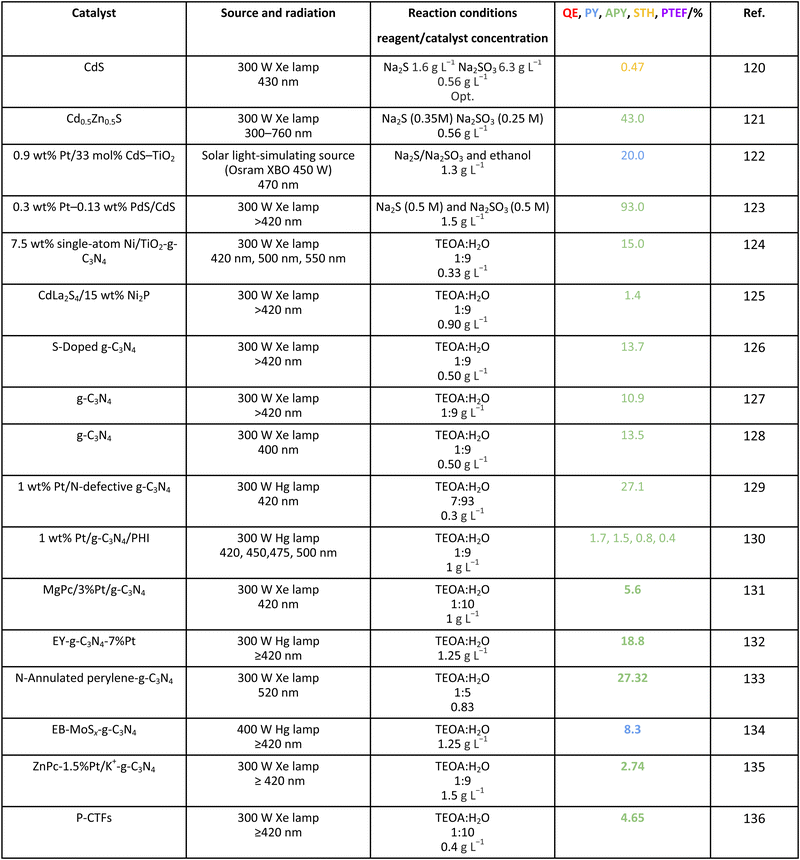
For the case of water splitting, Table 2 collects the data of efficiency. Of course, selectivity issues are trivial as hydrogen is the only possible product containing hydrogen atoms. Typical systems tested are composite systems based on oxides, oxysulfides, oxynitrides, nitrides and carbon nitride. As well described in the literature, such catalysts work under different Z-scheme type schemes allowing efficient charge carrier species separation and semi-reactions for hole and electron species at separated surface sites.3,19,20 Although the results using monochromatic sources (the 3 entries listed at the end of Table 2) can reach high values, when attempting to profit from the whole visible range, performance is significantly affected. Under polychromatic excitation, note that some values reported in the table and using the apparent yield/quantum efficiency (APY) are relatively high. This would likely indicate that the simple way of measuring efficiency is not only obsolete, as dictated by the IUPAC, but likely would lead to unphysical values in a significant number of cases. The STH values provided are always below or around 1%. Only in the case of a platinum promoted COF, we find a value exceeding the above mentioned cut-off.34 Despite this, for a realistic test, using a 100 m2 surface exposed to sunlight during a long period of time, the group of Domen obtained a 0.76% value for the STH parameter (1st entry of Table 2).35 The absence of information considering the measurement of the quantum efficiency can be noticed and thus the potential of the tested systems would need to be further assessed. Nevertheless, it can be concluded that the current status of water splitting is far from reaching the objective of using 10% of the sunlight energy.3.2. Methanol
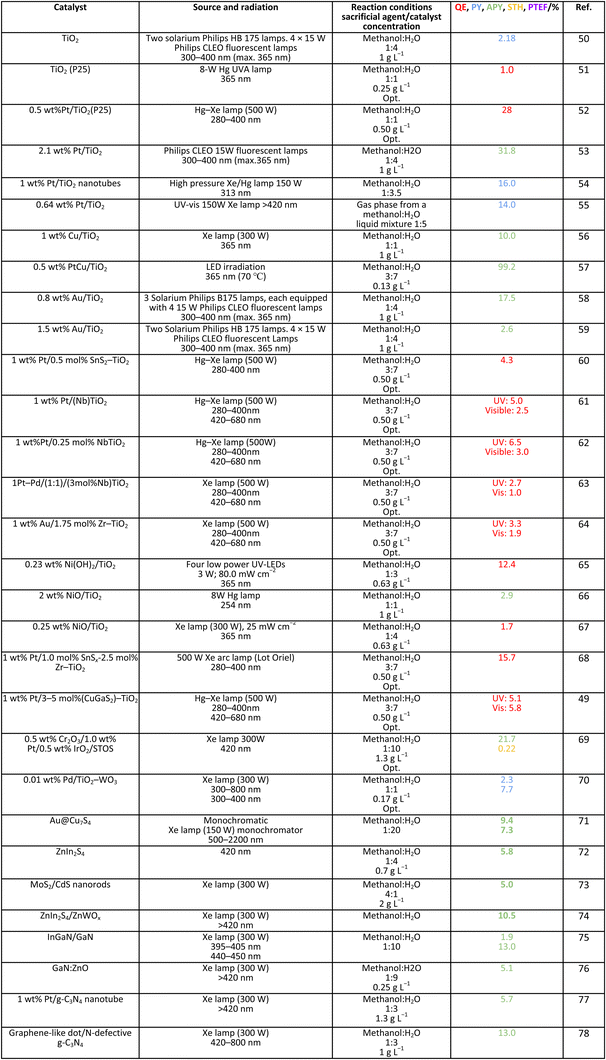
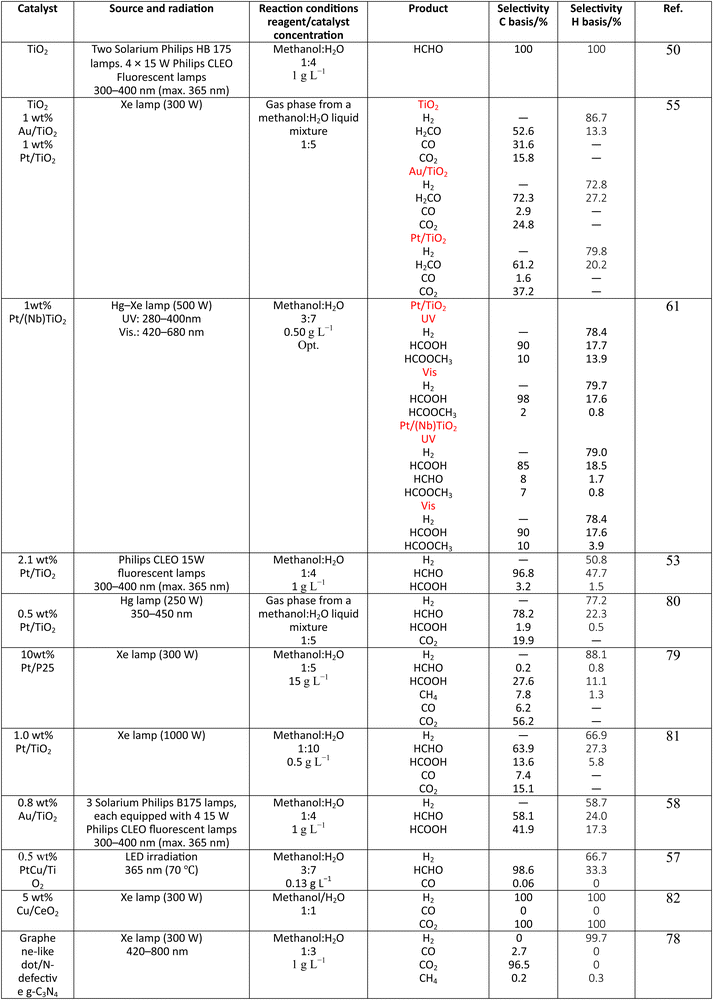
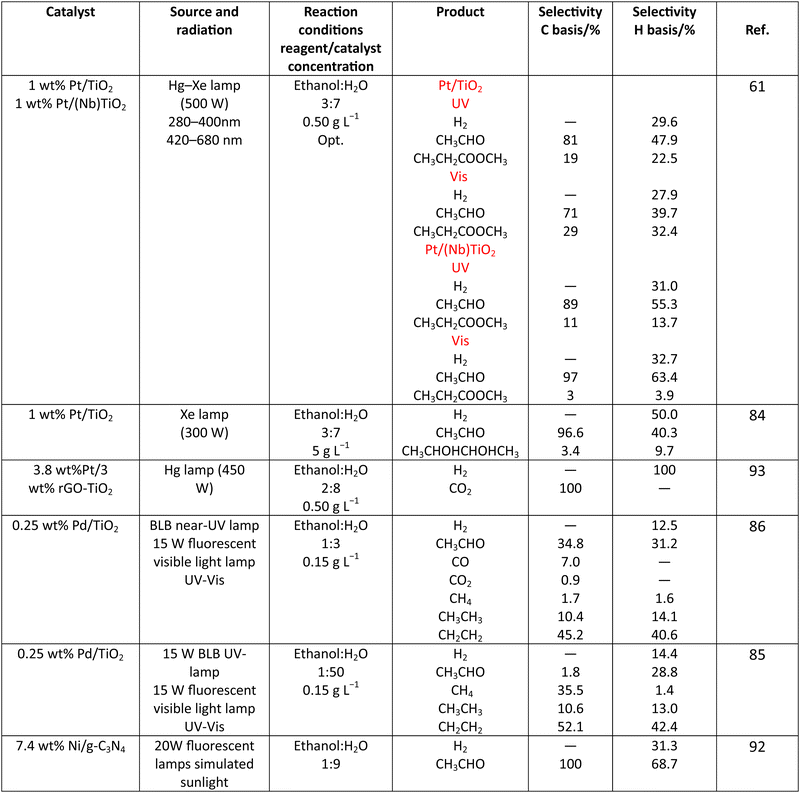
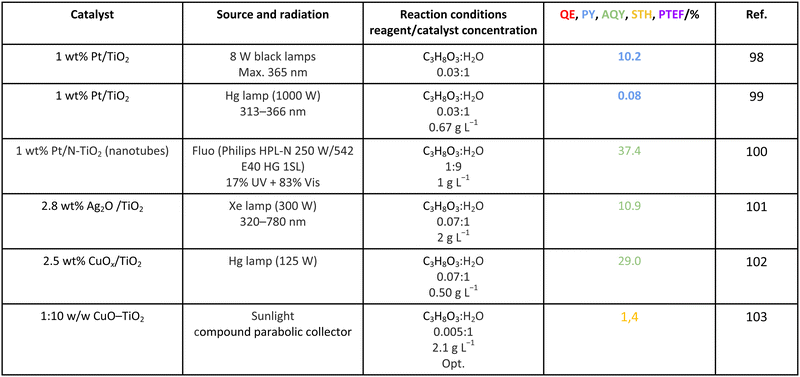
Methanol is selected as the initial carbon-containing sacrificial molecule here studied. It corresponds to the case more broadly studied. Also, the relative simplicity of the molecule allows for tracking all (carbon, oxygen and hydrogen containing) products potentially produced under reaction conditions. The summary of efficiency values reported is presented in Table 3. In this table, we selected as initial entries titania-based systems, promoted with Pt and other (noble and non-noble) co-catalysts as well as those systems obtained through doping of titania and/or composites with a dominant presence of the mentioned oxide. The corresponding results included in Table 3 are followed by other systems based on other oxides and thus other semiconductors, mostly sulfides and carbon nitride. Very high values are typically encountered when using the apparent photonic yield (APY), also called the apparent quantum yield. This has been commented already for the table considering water splitting results. The titania-based systems are reported mostly under UV irradiation and, in some cases, under visible irradiation. Efficiency under visible light is always inferior except for cases concerning composite systems where a second semiconductor is specifically devised for it. In any case, for the complete UV-visible range of sunlight (ca. 280–760 nm), all systems display an efficiency below ca. 6–7% (maximum achieved to our knowledge in ref. 49). Higher values can be encountered under UV illumination. The maximum of 6–7% could be achieved with other systems like carbon nitride, ZnIn2S4-based, or doped GaN systems (last entries of Table 3), although the absence of accurate calculations of the quantum efficiency does not allow one to establish this point with confidence for non-titania based systems. On the other hand, Table 3 would indicate the limited use of the STH or other non-IUPAC parameters when methanol is utilized to generate hydrogen. In summary, it can be considered that the best systems could be close to a real efficiency of 10% in the UV-visible range. Likely, the titania-based and other systems listed in Table 3 would not use efficiently the nearIR range, and thus there is room to improve and achieve efficient use of the sunlight full spectrum. A point to remark again is, however, that the energy release of all photons is not the same and although the nearIR range is very important, its energy content is significantly lower as well as more problematic to be used than that corresponding to the visible range, as already mentioned in the previous section.Interestingly, measuring the hydrogen generation from methanol using the quantum efficiency cannot take into account explicitly the number of charge carrier species utilized. Neither can it include chemical information. However, the photocatalytic reaction triggers the formation of a significant number of carbon, oxygen and hydrogen-containing molecules, with direct consequences in the production of hydrogen. This comes out for the presence of hydrogen in such molecules, limiting the production of molecular hydrogen. Table 4 captures the most relevant works where the selectivity of the reaction has been explored and reported. It contains information of the selectivity on carbon and hydrogen atomic bases. Due to the relative simplicity of the reactant(s), methanol and water, all potential products of the reactions have been reported if considered the works previoulsy reported collectively. The summary of the evolution of the reactants and the concomitant production of hydrogen is presented in Fig. 1. Under illumination, after charge separation and creation of electron–hole pairs, two different radicals would be formed from the hole-related species attack on the sacrificial molecule. The most typical products are related to the initial production of an oxygen-type radical generated by the mentioned hole-type attack on the OH moiety, leading to an oxygen-centered alkoxy-type radical. This radical is highlighted with a green colour in Fig. 1. The subsequent (further) radical attack by hole-type species renders the carbon-containing oxidized species as well as protons. In a chain-type mechanism, formaldehyde, formic acid and carbon dioxide would be formed. It is important to note that formaldehyde is formed in a dehydrogenation step while the formation of the next intermediate, formic acid, involves water in a reforming-type step. This point is highlighted using a magenta colour for an oxygen atom in Fig. 1. To generate this (and subsequent) intermediates, protons are extracted from the two reactant molecules (although we did not use the magenta colour in carbon dioxide and other molecules generated from the acid intermediate and included in Fig. 1).55,61,79 Formation of carbon dioxide can be considered as a final step of the chain-type mechanism, but decarbonylation steps and production of carbon monoxide with subsequent triggering of the water gas shift reaction have been also shown to be involved in the reaction. In addition, coupling of methanol molecules activated through the alkoxy route can lead to the formation of methyl formate species.78,79 As said, each step generates concomitantly hydrogen ions consuming the hole-type radicals in a one-by-one ratio. The number of hole-type charge carrier/hydrogen ions is counted using the last observable in Fig. 1. This information is key to obtaining the selectivity factor. In addition to this path, the formation of a carbon-centered radical (highlighted with an orange colour in Fig. 1) can also take place, generating through a coupling step, as a first intermediate, ethylene glycol, a C2 molecule. The further evolution of ethylene glycol leads to other C2 molecules as well as C3 molecules formed with methanol molecules activated using exclusively the carbon-centered route or, in specific C2+ cases, a mixture of the paths. In subsequent steps, it is obvious that this (carbon-centered radical) route can also lead to C1 products including carbon dioxides.68,73 Again, we remark that formation of the (acetic) acid intermediate requires the use of water, as indicated in Fig. 1. In all cases (see the upper part of Fig. 1), the generation of the hydrogen molecule takes place from the hydrogen ions concomitantly originated with the carbon-containing intermediates and electrons, closing the catalytic cycle. Nevertheless, the presence of products which compete for the electrons (and holes through the consumption of hydrogen ions) is also encountered. This leads to the formation of hydrocarbon species, which are detected in a few studies when using methanol.78,79
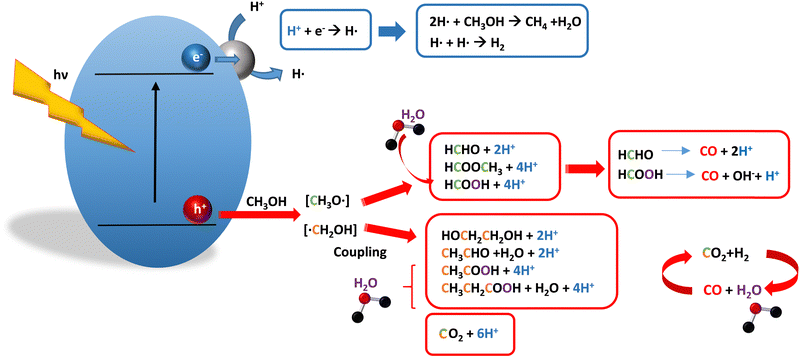 | ||
| Fig. 1 Schematic representation of the radical species and intermediates detected in the photocatalytic production using methanol as a sacrificial molecule. Colour codes are explained in the text. | ||
From Fig. 1 we can progress in the utilization of adequate engineering efficiency factor(s) with the claimed dual aim of enclosing information concerning energy but also sustainability. In particular, we would discuss the consequences of using the selectivity factor and the potential of the “fraction of useful photons” factor, ηΘ. For each molecule of hydrogen generated, essentially all steps of Fig. 1 would use two hole-type radicals. Thus for a pure photocatalytic, radical-triggered mechanism, whatever the selectivity, the S factor takes a value of 1/2 in the denominator of the efficiency, or in other words, the mentioned factor 2 multiplying the reaction rate in the numerator. This is true as far as thermal contributions to decarbonylation steps do not affect significantly the production of hydrogen. ηΘ(H2) has always a constant factor of 2 differing from the quantum efficiency. A different question is the calculation of ηΘ(H). If “electron-consuming” products like hydrocarbons are generated in the process, the (weighted) sum of the hydrogen and methane reaction rates should be considered in the calculation, and, critically important, the selectivity factor per H atom is different for these two products (Fig. 1). Of course, all hydrogen containing products should be included in the calculation of ηΘ(H) but carbon-containing molecules presented in Fig. 1 and generated using hole-type species have a trivial treatment of the selectivity factor, as discussed above. Therefore, due to the inherent properties of the ηΘ parameter, the ratio of ηΘ(H2) vs. ηΘ(H) expresses the atom-efficiency for the generation of hydrogen (ions) in terms of the “fraction” of photons consumed in the generation of the hydrogen molecule vs. the total photons used in the process that consumes the “generation” of H atoms. The ηΘ parameter can thus braid energy and sustainability information. This ηΘ(H2) observable is the most informative factor describing the (energy-related) efficiency of the reaction as it measures the faction of initial photons used to generate hydrogen and can be used straightforwardly in the calculation of the global efficiency of the process. Besides that, the above mentioned ηΘ(H2) vs. ηΘ(H) ratio allows the inclusion of sustainability related to the atom-efficiency in the use of hydrogen atoms by the photocatalytic system. We again recall that depending on the reaction products encountered (Table 3 and Fig. 1), the hydrogen atoms come from the sacrificial molecules exclusively or also from water.
As discussed in the introduction, a parallel point is the selective formation of specific carbon-containing intermediates. This fact can contribute to making the process “fully” sustainable. Examples of catalysts having high selectivity on a carbon basis are presented in Table 3. Of course, we can delineate the ηΘ(Cp) vs. ηΘ(C) ratio to analyze the carbon-based selectivity of the reaction on a photon basis. In this ratio, ηΘ(Cp) is the fraction of useful photons utilized to obtain the desired (carbon-containing) products. From Fig. 1 and the procedures outlined above, we can calculate easily the selectivity factors for the ηΘ(Cp) and ηΘ(C) parameters. A simple inspection of the figure shows that the calculation of the selectivity factor corresponding to ηΘ(Cp) is not as simple as the case of ηΘ(H2), that is, is not a constant.
3.3. Ethanol
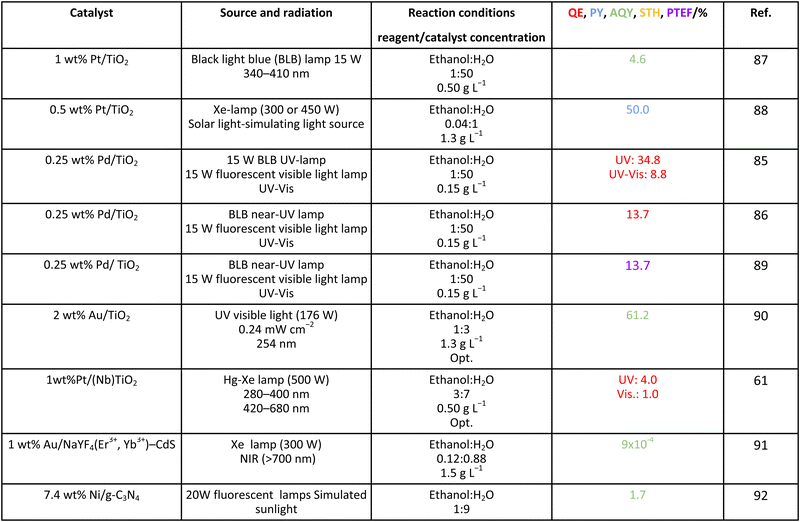
As it is obvious, in the case of ethanol, more intermediates could be formed but several potentially feasible paths are not supported by experimental evidence. In any case, Table 5 summarizes efficiency values for the production of hydrogen using this molecule. The results concerning efficiency parameters allowing quantitative measurement mainly concern titania-based systems, promoted with different noble metals and/or doping. A few non-titania systems are collected at the end of the table. From the inspection of Table 5, it is also plausible that the true efficiency, as measured by the quantum efficiency, can reach a value of around 10% using this molecule. The results concern the use of the UV-visible region although up to ca. 600 nm, but not the whole UV-visible-nearIR range of the solar spectrum. Considering the evolution of the sacrificial molecule, Table 6 collects the reports with careful investigation of the selectivity and Fig. 2 summarizes the results. We encountered relatively similar results to the more explored case of methanol. As can be seen in Fig. 2, the hole-triggered radicals detected are two. One oxygen-centered alkoxy-type radical and one carbon-centered radical corresponding to the CH3 moiety of the alcohol molecule. Other possible radicals are rather unlikely and unstable. Similarly to the methanol case, the alkoxy radical leads to the chain-type mechanism generating acetaldehyde, acetic acid and carbon dioxide. Decarbonylation reactions, the subsequent water gas shift equilibrium reaction, as well as “coupling” intermediates such as ethyl acetate can be also generated through this path. In addition, C1 products generated from the rupture of the C–C bond are sometimes observed.61,83 From the carbon-centered radical, we are only aware of the selective generation (96.6% selectivity on a carbon basis) of 2,3-butanediol (Table 5 and Fig. 2).84 In the case of ethanol, the presence of hydrocarbons was again detected, but a higher number of such molecules can be formed (Fig. 2).85,86 With the reaction scheme being rather parallel to the ethanol case, except for the C–C breaking products, the analysis described above essentially holds for the ethanol case. Thus, the mentioned possible achievement of a 10% profit of sunlight appears feasible and supported by the results of Table 5, although with the associated challenges just outlined for the methanol case. On the other hand, the generation of a significant number of products challenges the obtaining of high selectivity on a carbon basis, although Table 6 includes some cases. It is also evident that both the frequent presence of hydrocarbons as products and the relatively low selectivity to carbon dioxide (or, in other words, the higher number of products) observed in the majority of cases would lead to lower values of the ηΘ(H2) vs. ηΘ(H) ratio. Thus, the sustainability of ethanol as a sacrificial molecule for hydrogen generation would not reach values as in the case of methanol.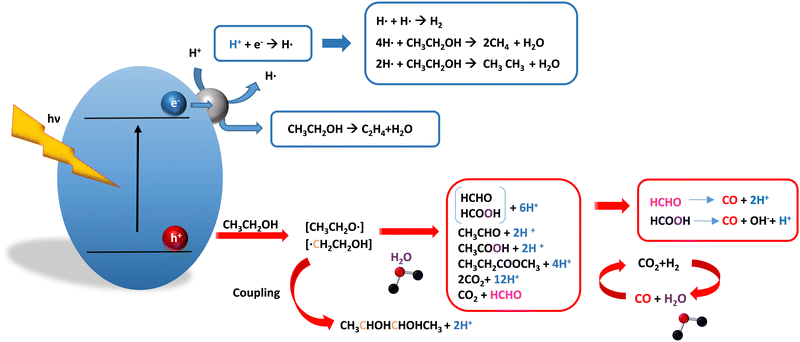 | ||
| Fig. 2 Schematic representation of the radical species and intermediates detected in the photocatalytic production using ethanol as a sacrificial molecule. Colour codes are explained in the text. | ||
3.4. Glycerol
For glycerol, data concerning efficiency values are presented in Table 7. Although the results are encouraging, a complete lack of reports containing information extracted from the quantum efficiency parameter can be noticed. The STH parameter could render a value near 1% under sunlight excitation. This indicates that glycerol would be a far more thought molecule to obtain a significant profit from sunlight. There are several studies analyzing qualitatively (e.g. detection of products) the evolution of the glycerol molecule in the reaction. These studies used titania-based materials and are summarized in Fig. 3, where we can see that only oxygen-centered radicals are considered for the formation of intermediates. The formation of electron-consuming products, competing with hydrogen, was also reported.94–96 As shown in Table 8, only a couple of contributions reported the full analysis of the selectivity,96,97 and thus there is limited information in this case to progress in the quantitative analysis of energy and sustainability issues.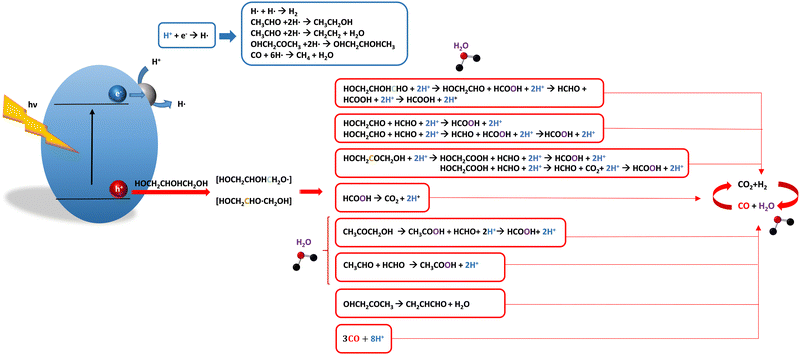 | ||
| Fig. 3 Schematic representation of the radical species and intermediates detected in the photocatalytic production using glycerol as a sacrificial molecule. Colour codes are explained in the text. | ||
| Catalyst | Source and radiation | Reaction conditions reagent/catalyst concentration | Product | Selectivity C basis/% | Selectivity H basis/% | Ref. |
|---|---|---|---|---|---|---|
| 1 wt% Rh/TiO2 | 300 W Xe lamp | C3H8O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O |
H2 | — | 70.8 | 96 |
| 0.75 g L−1 | C2H4O2 | 61.2 | 29.2 | |||
| CO2 | 38.8 | — | ||||
| 0.1 wt% Ag–0.3 wt% Pd/TiO2 | 100 W UV lamp | C3H8O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O |
H2 | — | 2.2 | 97 |
| ≥360 nm | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
CO | 0.08 | — | ||
| 0.25 g L−1 | CO2 | 2.4 | — | |||
| HCHO | 21.0 | 20.3 | ||||
| C2H6O2 | 7.4 | 10.7 | ||||
| C3H6O2 | 69.1 | 66.8 |
3.5. Other sacrificial molecules
We can briefly discuss the case of carbon-containing molecules using other (than those previously studied here) biomass-derived molecules which may strengthen the sustainability of the process. Table 9 summarizes the results considering other alcohols such as ethylene glycol and 2-propanol, acids such as lactic acid and ascorbic acid, sugars such as glucose, as well as more complex substrates such as 2,5-dimethylfuran, alpha-cellulose and lignocellulose. Catalysts utilized are oxides, nitrides, sulfides, MOFs, or carbon nitride sensitized with dyes, porphyrins or phthalocyanines. Similarly to the glycerol case, there is limited information although a couple of results using the photonic yield parameter suggest that glucose can be an ideal choice for generating hydrogen. The selectivity of the reaction is scarcely studied. Table 10 summarizes a couple of results encountered where the production of diesel precursors from 2,5-DMF104 or of pyruvic acid from lactic acid105 is achieved with high (carbon basis) selectivity and with the concomitant production of hydrogen. It can be also mentioned that hydrogen generation from biomolecules, for example ethanol, can be used in a cascade-type process to trigger hydrogenation steps of other biomolecules to render valuable products, such as benzimidazole derivatives.106| Catalyst | Source and radiation | Reaction conditions reagent/catalyst concentration | Product | Selectivity C basis/% | Selectivity H basis/% | Ref. |
|---|---|---|---|---|---|---|
| 0.1 wt% Ru/ZnIn2S4 | LED irradiation (9.6 W) | CH3CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,5-DMF 2,5-DMF |
H2 | — | 63.3 | 104 |
| 455 nm | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Dimers (C12) | 68.3 | 17.8 | ||
| 10 g L−1 | Trimers (C18) | 28.3 | 4.0 | |||
| Tetramers (C24) | 3.3 | 14.8 | ||||
| 5 wt% Pt/CdS | 1000 W Xe lamp | Lactic acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O |
H2 | — | 45.1 | 105 |
| 430–520 nm | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
CO2 | 2.1 | — | ||
| 6 g L−1 | CH3COCOOH | 97.9 | 54.9 | |||
Finally, for completeness, we collected selected results for efficiency calculations using other sacrificial molecules of use in the field such as TEOA. The results are compiled in Table 11. The catalysts employed with this sacrificial agent included the frequently utilized molecular-type catalysts such as carbon nitride but also composite systems with dyes such as erythrosine B and eosin Y, as well as porphyrins or phthalocyanines. High values of efficiency can be observed in several cases but using parameters having a limited utility, as earlier discussed in this work using methanol, where a most complete database is available. Thus, their potential to achieve the 10% profit from solar light is still to be ascertained.
4. Conclusions
Nowadays, the photocatalytic generation of hydrogen attempts to produce this energy vector using renewable energy sources and reactants. To reach a holistic approach towards the settlement of a clean, green hydrogen production and explore the future of the process, the setting up of parameters allowing a quantitative measurement of both the energetic and sustainability implications of the process appears as a must.To this end, here we surveyed the literature available parameters primarily oriented to measuring efficiency. Efficiency parameters are defined by the IUPAC for photocatalytic processes, with quantum efficiency being the one that allows a rigorous metrics to evaluate the global efficiency of a process. From this, we delineated the work aiming to progress further in the evaluation of both energetic and sustainability sides of the hydrogen photocatalytic process using a quantum efficiency related parameter, the so-called “fraction of useful photons”. This parameter allows the true calculation of the global efficiency, rendering a dimensionless parameter, but also expresses the hydrogen atom efficiency of hydrogen production in a photon-based metrics. In addition, up to four additional parameters, all of them demanding less experimental–computational effort in their calculation, were considered. These go from the photonic yield parameter defined by the IUPAC, to other broadly used parameters such as the solar-to-hydrogen efficiency. These parameters focus on the energetic side of the problem but, unfortunately, would not inform straightforwardly about the possible energy-related losses and the ways to circumvent them. In spite of it, their simplicity compared with the quantum efficiency related parameters makes their use broad and appealing. The article also described briefly the application of new tools based on artificial intelligence in the field. We stressed the point that the results would indicate that the knowledge of the rate of photon absorption or simpler yet related parameters appears unavoidable to obtain useful information.
We utilized the set of six parameters (quantum efficiency, fraction of useful photons, photonic yield, apparent (photonic) yield, solar-to-hydrogen and photochemical thermodynamic efficiency factor) to evaluate the field of photocatalytic production of hydrogen. In parallel, the perspective article paid particular attention to the interpretation of the physical basis of the quantum efficiency and the fraction of useful photon parameters. We sorted out the research published in the field considering the different catalytic processes studied. Starting with the use of water in the splitting reaction, we analyzed the use of different sacrificial molecules, paying particular attention to the use of renewable sacrificial molecules, particularly alcohols which can come from fermentation and other bio-based processes.
With water being a potentially optimal reactant, the results of the literature considering the whole use of the solar spectrum would indicate that research output is far from achieving the benchmark value of 10%. For sacrificial molecules, analysis of the dual-aim “fraction of useful photons” parameter was carried out in terms of both the charge-carrier utilization and the molecules’ (and water) roles and evolution under reaction conditions, and the result utilized to interpret the capability of any catalytic system in terms of energy and sustainability and thus to serve as a firm ground to guide the future of the field. The survey of the sacrificial molecules studied in the literature would indicate that methanol and (to a somewhat lower extent) ethanol can be optimal choices. Glucose could be also a good choice in terms of energy related issues. For the cases of methanol and ethanol, it appears that titania-based composite systems are close to the 10% cuff-off value in the UV-visible range, but the efficient use of the complete solar spectrum is still challenging. In particular, the nearIR region would need to be fruitfully utilized. According to the literature results, this would require a more intensive exploration of multicomponent composite systems, where, in addition to the co-catalyst presence, the (titania) oxide based systems would be doped and/or accompanied with lanthanide and/or carbon elements (doping) and semiconductors (composite). A more exhaustive analysis of other alternatives, such as the two photon technologies, awaits in the future in order to show potential in the field.
The analysis has been extended to other sacrificial molecules of interest, such as glycerol coming from the transesterification of fatty acids (triglycerides) and other processes, or less commonly tested molecules such as isopropanol, lignin acid, and others. Unfortunately, the limited and (relatively) low quality of the information precludes any rigorous analysis, although in most cases, the benchmark value of 10% of the solar spectrum light appears unattainable with current capabilities.
Acronyms
Data availability
Data will be available upon request to the authors.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the financial support through grant and PID2022-136883OB-C21. The project is funded by MCIN/AEI/10.13039/501100011033 (Spain). M. F. G. is deeply indebted to Prof. F. Fernández-Martín for multiple discussions.References
- J. Zhao, R. Shi, Z. Li, C. Zhou and T. Zhang, Nano Sel., 2020, 1, 12–29 CrossRef.
- U. Mondal and G. D. Yadav, Green Chem., 2021, 23, 8361–8405 RSC.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef PubMed.
- A. Kubacka, M. Fernández-García and G. Colón, Chem. Rev., 2012, 112, 1555–1614 CrossRef CAS PubMed.
- D. Rodríguez-Padrón, R. Luque and M. J. Muñoz-Batista, Top. Curr. Chem., 2020, 378, 1–28 CrossRef PubMed.
- S. Alsayegh, J. R. Johnson, B. Ohs, J. Lohaus and M. Wessling, Int. J. Hydrogen Energy, 2017, 42, 6000–6011 CrossRef CAS.
- H. Idriss, Energy Technol., 2021, 9, 2000843 CrossRef CAS.
- V. Kumaravel, M. Imam, A. Badreldin, R. Chava, J. Do, M. Kang and A. Abdel-Wahab, Catalysts, 2019, 9, 276 CrossRef CAS.
- M. Ismael, Sol. Energy, 2020, 211, 522–546 CrossRef CAS.
- H. H. Do, D. L. T. Nguyen, X. C. Nguyen, T.-H. Le, T. P. Nguyen, Q. T. Trinh, S. H. Ahn, D.-V. N. Vo, S. Y. Kim and Q. Van Le, Arabian J. Chem., 2020, 13, 3653–3671 CrossRef CAS.
- R. Liu, H. Yin, P. Guo, X. Liu and Z. Yin, Energy Technol., 2024, 2301708 CrossRef.
- O. M. Alfano, D. Bahnemann, A. E. Cassano, R. Dillert and R. Goslich, Catal. Today, 2000, 58, 199–230 CrossRef CAS.
- U. Caudillo-Flores, M. J. Muñoz-Batista, M. Fernández-García and A. Kubacka, Catal. Rev., 2024, 66, 531–585 CrossRef CAS.
- M. Qureshi and K. Takanabe, Chem. Mater., 2017, 29, 158–167 CrossRef CAS.
- A. Kubacka, I. Barba-Nieto, U. Caudillo-Flores and M. Fernández-García, Curr. Opin. Chem. Eng., 2021, 33, 100712 CrossRef.
- S. E. Braslavsky, A. M. Braun, A. E. Cassano, A. V. Emeline, M. I. Litter, L. Palmisano, V. N. Parmon and N. Serpone, Pure Appl. Chem., 2011, 83, 931–1014 CrossRef CAS.
- M. Melchionna and P. Fornasiero, ACS Catal., 2020, 10, 5493–5501 CrossRef.
- Z. Chen, T. F. Jaramillo, T. G. Deutsch, A. Kleiman-Shwarsctein, A. J. Forman, N. Gaillard, R. Garland, K. Takanabe, C. Heske, M. Sunkara, E. W. McFarland, K. Domen, E. L. Miller, J. A. Turner and H. N. Dinh, J. Mater. Res., 2010, 25, 3–16 CrossRef.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef.
- S. Cao and L. Piao, Angew. Chem., Int. Ed., 2020, 59, 18312–18320 CrossRef PubMed.
- L. Sun and J. R. Bolton, J. Phys. Chem., 1996, 100, 4127–4134 CrossRef.
- H. de Lasa, B. S. Rosales, J. Moreira and P. Valades-Pelayo, Chem. Eng. Technol., 2016, 39, 51–65 CrossRef CAS.
- F. Machuca-Martínez, M. A. Mueses, J. Colina-Márquez and G. L. Puma, Photocatalytic Reactor Modeling, RSC, 2016, ch. 16, pp. 388–424 Search PubMed.
- Y. Boyjoo, H. Sun, J. Liu, V. K. Pareek and S. Wang, Chem. Eng. J., 2017, 310, 537–559 CrossRef CAS.
- L. Zhang and W. A. Anderson, Chem. Eng. Sci., 2010, 65, 1513–1521 CrossRef CAS.
- J. E. Duran, F. Taghipour and M. Mohseni, J. Photochem. Photobiol., A, 2010, 215, 81–89 CrossRef CAS.
- Y. Boyjoo, M. Ang and V. Pareek, Chem. Eng. Sci., 2014, 111, 34–40 CrossRef CAS.
- J. Moreno, C. Casado and J. Marugán, Chem. Eng. Sci., 2019, 205, 151–164 CrossRef CAS.
- O. M. Alfano, A. E. Cassano, J. Marugán and R. van Grieken, Fundamentals of Radiation Transport in Absorbing Scattering Media, RSC, 2016, ch. 14, pp. 349–366 Search PubMed.
- Y. Haghshenas, W. P. Wong, D. Gunawan, A. Khataee, R. Keyikoğlu, A. Razmjou, P. V. Kumar, C. Y. Toe, H. Masood, R. Amal, V. Sethu and W. Y. Teoh, EES Catal., 2024, 2, 612–623 RSC.
- A. Kubacka, U. Caudillo-Flores, I. Barba-Nieto and M. Fernández-García, Appl. Catal., A, 2021, 610, 117966 CrossRef CAS.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983 RSC.
- A. Gupta, B. Likozar, R. Jana, W. C. Chanu and M. K. Singh, Int. J. Hydrogen Energy, 2022, 47, 33282–33307 CrossRef CAS.
- Y. Yang, X. Chu, H.-Y. Zhang, R. Zhang, Y.-H. Liu, F.-M. Zhang, M. Lu, Z.-D. Yang and Y.-Q. Lan, Nat. Commun., 2023, 14, 593 CrossRef CAS.
- H. Nishiyama, T. Yamada, M. Nakabayashi, Y. Maehara, M. Yamaguchi, Y. Kuromiya, Y. Nagatsuma, H. Tokudome, S. Akiyama, T. Watanabe, R. Narushima, S. Okunaka, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Nature, 2021, 598, 304–307 CrossRef CAS.
- H. Kato, Y. Sasaki, N. Shirakura and A. Kudo, J. Mater. Chem. A, 2013, 1, 12327 RSC.
- Q. Wang, T. Hisatomi, Q. Jia, H. Tokudome, M. Zhong, C. Wang, Z. Pan, T. Takata, M. Nakabayashi, N. Shibata, Y. Li, I. D. Sharp, A. Kudo, T. Yamada and K. Domen, Nat. Mater., 2016, 15, 611–615 CrossRef PubMed.
- Q. Wang, T. Hisatomi, Y. Suzuki, Z. Pan, J. Seo, M. Katayama, T. Minegishi, H. Nishiyama, T. Takata, K. Seki, A. Kudo, T. Yamada and K. Domen, J. Am. Chem. Soc., 2017, 139, 1675–1683 CrossRef PubMed.
- K. Sayama, K. Mukasa, R. Abe, Y. Abe and H. Arakawa, Chem. Commun., 2001, 2416–2417 RSC.
- J. Kim, D. W. Hwang, H. G. Kim, S. W. Bae, J. S. Lee, W. Li and S. H. Oh, Top. Catal., 2005, 35, 295–303 CrossRef.
- S. Sun, T. Hisatomi, Q. Wang, S. Chen, G. Ma, J. Liu, S. Nandy, T. Minegishi, M. Katayama and K. Domen, ACS Catal., 2018, 8, 1690–1696 CrossRef.
- R. Abe, T. Takata, H. Sugihara and K. Domen, Chem. Commun., 2005, 3829 RSC.
- K. Maeda, M. Higashi, D. Lu, R. Abe and K. Domen, J. Am. Chem. Soc., 2010, 132, 5858–5868 CrossRef CAS PubMed.
- X. Chen, R. Shi, Q. Chen, Z. Zhang, W. Jiang, Y. Zhu and T. Zhang, Nano Energy, 2019, 59, 644–650 Search PubMed.
- H. Su, W. Che, F. Tang, W. Cheng, X. Zhao, H. Zhang and Q. Liu, J. Phys. Chem. C, 2018, 122, 21108–21114 Search PubMed.
- Y. Goto, T. Hisatomi, Q. Wang, T. Higashi, K. Ishikiriyama, T. Maeda, Y. Sakata, S. Okunaka, H. Tokudome, M. Katayama, S. Akiyama, H. Nishiyama, Y. Inoue, T. Takewaki, T. Setoyama, T. Minegishi, T. Takata, T. Yamada and K. Domen, Joule, 2018, 2, 509–520 CrossRef CAS.
- T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414 Search PubMed.
- H. Kato and A. Kudo, J. Phys. Chem. B, 2001, 105, 4285–4292 CrossRef CAS.
- U. Caudillo-Flores, A. Kubacka, T. Berestok, T. Zhang, J. Llorca, J. Arbiol, A. Cabot and M. Fernández-García, Int. J. Hydrogen Energy, 2020, 45, 1510–1520 CrossRef CAS.
- E. Pulido Melián, O. González Díaz, A. Ortega Méndez, C. R. López, M. Nereida Suárez, J. M. Doña Rodríguez, J. A. Navío, D. Fernández Hevia and J. Pérez Peña, Int. J. Hydrogen Energy, 2013, 38, 2144–2155 CrossRef.
- M. Edelmannová, M. de los Milagros Ballari, M. Přibyl and K. Kočí, Energy Convers. Manage., 2021, 245, 114582 Search PubMed.
- O. Fontelles-Carceller, M. J. Muñoz-Batista, E. Rodríguez-Castellón, J. C. Conesa, M. Fernández-García and A. Kubacka, J. Catal., 2017, 347, 157–169 Search PubMed.
- E. P. Melián, C. R. López, A. O. Méndez, O. G. Díaz, M. N. Suárez, J. M. D. Rodríguez, J. A. Navío and D. F. Hevia, Int. J. Hydrogen Energy, 2013, 38, 11737–11748 CrossRef.
- M. P. Languer, F. R. Scheffer, A. F. Feil, D. L. Baptista, P. Migowski, G. J. Machado, D. P. de Moraes, J. Dupont, S. R. Teixeira and D. E. Weibel, Int. J. Hydrogen Energy, 2013, 38, 14440–14450 Search PubMed.
- A. Naldoni, M. D’Arienzo, M. Altomare, M. Marelli, R. Scotti, F. Morazzoni, E. Selli and V. Dal Santo, Appl. Catal., B, 2013, 130–131, 239–248 CrossRef CAS.
- K. Ćwieka, Z. Bojarska, K. Czelej, D. Łomot, P. Dziegielewski, A. Maximenko, K. Nikiforow, L. Gradoń, M. Qi, Y. Xu and J. C. Colmenares, Chem. Eng. J., 2023, 474, 145687 CrossRef.
- H. Wang, H. Qi, X. Sun, S. Jia, X. Li, T. J. Miao, L. Xiong, S. Wang, X. Zhang, X. Liu, A. Wang, T. Zhang, W. Huang and J. Tang, Nat. Mater., 2023, 22, 619–626 CrossRef CAS PubMed.
- J. A. Ortega Méndez, C. R. López, E. Pulido Melián, O. González Díaz, J. M. Doña Rodríguez, D. Fernández Hevia and M. Macías, Appl. Catal., B, 2014, 147, 439–452 CrossRef.
- E. Pulido Melián, M. Nereida Suárez, T. Jardiel, D. G. Calatayud, A. del Campo, J. M. Doña-Rodríguez, J. Araña and O. M. González Díaz, Int. J. Hydrogen Energy, 2019, 44, 24653–24666 CrossRef.
- I. Barba-Nieto, K. C. Christoforidis, M. Fernández-García and A. Kubacka, Appl. Catal., B, 2020, 277, 119246 Search PubMed.
- O. Fontelles-Carceller, M. J. Muñoz-Batista, J. C. Conesa, A. Kubacka and M. Fernández-García, Mol. Catal., 2018, 446, 88–97 CrossRef CAS.
- O. Fontelles-Carceller, M. J. Muñoz-Batista, J. C. Conesa, M. Fernández-García and A. Kubacka, Appl. Catal., B, 2017, 216, 133–145 Search PubMed.
- U. Caudillo-Flores, M. J. Muñoz-Batista, M. Fernández-García and A. Kubacka, Appl. Catal., B, 2018, 238, 533–545 CrossRef CAS.
- L. A. Arce-Saldaña, U. Caudillo-Flores, R. Sayago-Carro, G. Soto-Herrera, M. Fernández-García and A. Kubacka, Catal. Today, 2023, 419, 114148 Search PubMed.
- J. Yu, Y. Hai and B. Cheng, J. Phys. Chem. C, 2011, 115, 4953–4958 CrossRef CAS.
- H. Wang, H. Jiang, P. Huo, M. Filip Edelmannová, L. Čapek and K. Kočí, J. Environ. Chem. Eng., 2022, 10, 106908 CrossRef CAS.
- L. Li, B. Cheng, Y. Wang and J. Yu, J. Colloid Interface Sci., 2015, 449, 115–121 CrossRef.
- I. Barba-Nieto, G. Colón, M. Fernández-García and A. Kubacka, Chem. Eng. J., 2022, 442, 136333 CrossRef.
- L. Lin, Y. Ma, J. J. M. Vequizo, M. Nakabayashi, C. Gu, X. Tao, H. Yoshida, Y. Pihosh, Y. Nishina, A. Yamakata, N. Shibata, T. Hisatomi, T. Takata and K. Domen, Nat. Commun., 2024, 15, 397 CrossRef PubMed.
- S. Y. Toledo Camacho, A. Rey, M. D. Hernández-Alonso, J. Llorca, F. Medina and S. Contreras, Appl. Surf. Sci., 2018, 455, 570–580 CrossRef.
- C.-W. Tsao, S. Narra, J.-C. Kao, Y.-C. Lin, C.-Y. Chen, Y.-C. Chin, Z.-J. Huang, W.-H. Huang, C.-C. Huang, C.-W. Luo, J.-P. Chou, S. Ogata, M. Sone, M. H. Huang, T.-F. M. Chang, Y.-C. Lo, Y.-G. Lin, E. W.-G. Diau and Y.-J. Hsu, Nat. Commun., 2024, 15, 413 CrossRef PubMed.
- R. Jiang, L. Mao, Y. Zhao, J. Zhang, X. Cai and X. Gu, J. Colloid Interface Sci., 2022, 606, 317–327 CrossRef PubMed.
- S. Xie, Z. Shen, J. Deng, P. Guo, Q. Zhang, H. Zhang, C. Ma, Z. Jiang, J. Cheng, D. Deng and Y. Wang, Nat. Commun., 2018, 9, 1181 CrossRef PubMed.
- X. Zheng, Y. Song, Y. Liu, Y. Yang, D. Wu, Y. Yang, S. Feng, J. Li, W. Liu, Y. Shen and X. Tian, Coord. Chem. Rev., 2023, 475, 214898 CrossRef.
- M. G. Kibria, H. P. T. Nguyen, K. Cui, S. Zhao, D. Liu, H. Guo, M. L. Trudeau, S. Paradis, A.-R. Hakima and Z. Mi, ACS Nano, 2013, 7, 7886–7893 CrossRef.
- K. Liu, B. Zhang, J. Zhang, W. Lin, J. Wang, Y. Xu, Y. Xiang, T. Hisatomi, K. Domen and G. Ma, ACS Catal., 2022, 12, 14637–14646 CrossRef.
- S. Guo, Z. Deng, M. Li, B. Jiang, C. Tian, Q. Pan and H. Fu, Angew. Chem., Int. Ed., 2016, 55, 1830–1834 CrossRef.
- R. Wang, X. Wang, X. Li, L. Pei, X. Gu and Z. Zheng, Int. J. Hydrogen Energy, 2021, 46, 197–208 CrossRef CAS.
- M. Bernareggi, G. L. Chiarello, G. West, M. Ratova, A. M. Ferretti, P. Kelly and E. Selli, Catal. Today, 2019, 326, 15–21 CrossRef CAS.
- G. L. Chiarello, M. H. Aguirre and E. Selli, J. Catal., 2010, 273, 182–190 CrossRef CAS.
- T. A. Kandiel, R. Dillert, L. Robben and D. W. Bahnemann, Catal. Today, 2011, 161, 196–201 CrossRef CAS.
- L. Zhao, M. Tang, F. Wang and X. Qiu, Fuel, 2023, 331, 125748 CrossRef CAS.
- D. S. Muggli, J. T. McCue and J. L. Falconer, J. Catal., 1998, 173, 470–483 CrossRef CAS.
- H. Lu, J. Zhao, L. Li, L. Gong, J. Zheng, L. Zhang, Z. Wang, J. Zhang and Z. Zhu, Energy Environ. Sci., 2011, 4, 3384 RSC.
- B. Rusinque, S. Escobedo and H. de Lasa, Catalysts, 2022, 12, 113 CrossRef CAS.
- B. Rusinque, S. Escobedo and H. de Lasa, Catalysts, 2021, 11, 405 CrossRef CAS.
- Y. Li, Y.-K. Peng, L. Hu, J. Zheng, D. Prabhakaran, S. Wu, T. J. Puchtler, M. Li, K.-Y. Wong, R. A. Taylor and S. C. E. Tsang, Nat. Commun., 2019, 10, 4421 CrossRef PubMed.
- D. I. Kondarides, V. M. Daskalaki, A. Patsoura and X. E. Verykios, Catal. Lett., 2008, 122, 26–32 CrossRef CAS.
- S. Escobedo, B. Rusinque and H. de Lasa, Ind. Eng. Chem. Res., 2019, 58, 22225–22235 CrossRef CAS.
- N. Kunthakudee, T. Puangpetch, P. Ramakul, K. Serivalsatit and M. Hunsom, Int. J. Hydrogen Energy, 2022, 47, 23570–23582 CrossRef CAS.
- W. Feng, L. Zhang, Y. Zhang, Y. Yang, Z. Fang, B. Wang, S. Zhang and P. Liu, J. Mater. Chem. A, 2017, 5, 10311–10320 RSC.
- D. Gunawan, C. Y. Toe, P. Kumar, J. Scott and R. Amal, ACS Appl. Mater. Interfaces, 2021, 13, 49916–49926 CrossRef CAS.
- M. A. Esteves, F. Fresno, V. R. Fernandes, F. E. Oropeza, V. A. de la Peña O’Shea and C. M. Rangel, Catal. Today, 2021, 380, 41–52 CrossRef CAS.
- M. C. Herrera-Beurnio, F. J. López-Tenllado, J. Hidalgo-Carrillo, J. Martín-Gómez, R. Estévez, F. J. Urbano and A. Marinas, Catal. Today, 2024, 430, 114548 CrossRef.
- S. Adhikari, S. D. Fernando and A. Haryanto, Energy Convers. Manage., 2009, 50, 2600–2604 CrossRef.
- K. E. Sanwald, T. F. Berto, W. Eisenreich, O. Y. Gutiérrez and J. A. Lercher, J. Catal., 2016, 344, 806–816 CrossRef.
- A. K. Wahab and H. Idriss, Int. J. Hydrogen Energy, 2024, 52, 159–171 CrossRef.
- N. Skillen, K. Ralphs, D. Craig, S. McCalmont, A. F. V. Muzio, C. O’Rourke, H. Manyar and P. K. J. Robertson, J. Chem. Technol. Biotechnol., 2020, 95, 2619–2627 CrossRef.
- M. Yasuda, T. Matsumoto and T. Yamashita, Glycerine Production and Transformation – An Innovative Platform for Sustainable Biorefinery and Energy, IntechOpen, 2019 Search PubMed.
- S. D. Tristantini, Valentina and M. Ibadurrohman, Int. J. Energy Res., 2013, 37, 1372–1381 CrossRef.
- C. Wang, X. Cai, Y. Chen, Z. Cheng, X. Luo, S. Mo, L. Jia, R. Shu, P. Lin, Z. Yang, S. Sun, E. Pu and Y. Shen, Int. J. Hydrogen Energy, 2017, 42, 17063–17074 CrossRef.
- V. Gombac, L. Sordelli, T. Montini, J. J. Delgado, A. Adamski, G. Adami, M. Cargnello, S. Bernal and P. Fornasiero, J. Phys. Chem. A, 2010, 114, 3916–3925 CrossRef PubMed.
- A. Ruiz-Aguirre, J. G. Villachica-Llamosas, M. I. Polo-López, A. Cabrera-Reina, G. Colón, J. Peral and S. Malato, Energy, 2022, 260, 125199 CrossRef.
- N. Luo, T. Montini, J. Zhang, P. Fornasiero, E. Fonda, T. Hou, W. Nie, J. Lu, J. Liu, M. Heggen, L. Lin, C. Ma, M. Wang, F. Fan, S. Jin and F. Wang, Nat. Energy, 2019, 4, 575–584 CrossRef.
- H. Harada, T. Sakata and T. Ueda, J. Phys. Chem., 1989, 93, 1542–1548 CrossRef.
- T. Montini, V. Gombac, J. J. Delgado, A. M. Venezia, G. Adami and P. Fornasiero, Inorg. Chim. Acta, 2021, 520, 120289 CrossRef CAS.
- R. Kumar, G. Swain and S. Dutta, Fuel, 2024, 360, 130555 CrossRef CAS.
- X. Wang, H. Yu, L. Yang, L. Shao and L. Xu, Catal. Commun., 2015, 67, 45–48 CrossRef CAS.
- W. Zhang, Y. Wang, Z. Wang, Z. Zhong and R. Xu, Chem. Commun., 2010, 46, 7631 RSC.
- X. Zong, G. Wu, H. Yan, G. Ma, J. Shi, F. Wen, L. Wang and C. Li, J. Phys. Chem. C, 2010, 114, 1963–1968 CrossRef CAS.
- C. Li, H. Wang, S. B. Naghadeh, J. Z. Zhang and P. Fang, Appl. Catal., B, 2018, 227, 229–239 CrossRef CAS.
- X. Zhang, L. Yu, C. Zhuang, T. Peng, R. Li and X. Li, ACS Catal., 2014, 4, 162–170 CrossRef CAS.
- L. Yu, X. Zhang, C. Zhuang, L. Lin, R. Li and T. Peng, Phys. Chem. Chem. Phys., 2014, 16, 4106 RSC.
- J. Wang, D. Liu, Q. Liu, T. Peng, R. Li and S. Zhou, Appl. Surf. Sci., 2019, 464, 255–261 CrossRef CAS.
- J. Wang, Y. Zheng, T. Peng, J. Zhang and R. Li, ACS Sustainable Chem. Eng., 2017, 5, 7549–7556 CrossRef CAS.
- A. Speltini, M. Sturini, F. Maraschi, D. Dondi, A. Serra, A. Profumo, A. Buttafava and A. Albini, Int. J. Hydrogen Energy, 2014, 39, 11433–11440 CrossRef CAS.
- Q. Cheng, Y.-J. Yuan, R. Tang, Q.-Y. Liu, L. Bao, P. Wang, J. Zhong, Z. Zhao, Z.-T. Yu and Z. Zou, ACS Catal., 2022, 12, 2118–2125 CrossRef CAS.
- P. Wang, Y. Yuan, Q. Liu, Q. Cheng, Z. Shen, Z. Yu and Z. Zou, ChemSusChem, 2021, 14, 2860–2865 CrossRef CAS.
- Z.-X. Huang, C. Ma, F.-G. Zhang, Q. Cheng, Q.-Y. Liu, Y.-J. Yuan and X. Zhang, J. Mater. Chem. A, 2023, 11, 7488–7497 RSC.
- D. Jing, H. Liu, X. Zhang, L. Zhao and L. Guo, Energy Convers. Manage., 2009, 50, 2919–2926 CrossRef CAS.
- M. Liu, L. Wang, G. (Max) Lu, X. Yao and L. Guo, Energy Environ. Sci., 2011, 4, 1372 RSC.
- V. M. Daskalaki, M. Antoniadou, G. Li Puma, D. I. Kondarides and P. Lianos, Environ. Sci. Technol., 2010, 44, 7200–7205 CrossRef CAS PubMed.
- H. Yan, J. Yang, G. Ma, G. Wu, X. Zong, Z. Lei, J. Shi and C. Li, J. Catal., 2009, 266, 165–168 CrossRef CAS.
- S. Yang, K. Wang, Q. Chen and Y. Wu, J. Mater. Sci. Technol., 2024, 175, 104–114 CrossRef.
- Y. Fan, S. Yu, Y. Wang, Y. Xie and X. Qiu, Sep. Purif. Technol., 2024, 335, 126243 CrossRef.
- T. Fei, C. Qin, Y. Zhang, G. Dong, Y. Wang, Y. Zhou and M. Cui, Int. J. Hydrogen Energy, 2021, 46, 20481–20491 CrossRef.
- J. Fang, F. Sun, A. Kheradmand, H. Xu, H. Dong, X. Yi, H. Hong and X. Liu, Fuel, 2023, 353, 129277 CrossRef.
- J. Huang, Y. Lu, H. Zhang, L. Shangguan, Z. Mou, J. Sun, S. Sun, J. He and W. Lei, Chem. Eng. J., 2021, 405, 126685 CrossRef.
- D. Liu, C. Zhang, J. Shi, Y. Shi, T. T. T. Nga, M. Liu, S. Shen and C. Dong, Small, 2024, 20, 2310289 CrossRef CAS.
- L. Mao, B. Zhai, J. Shi, X. Kang, B. Lu, Y. Liu, C. Cheng, H. Jin, E. Lichtfouse and L. Guo, ACS Nano, 2024, 18, 13939–13949 CrossRef CAS.
- K. Takanabe, K. Kamata, X. Wang, M. Antonietti, J. Kubota and K. Domen, Phys. Chem. Chem. Phys., 2010, 12, 13020 RSC.
- J. Xu, Y. Li, S. Peng, G. Lu and S. Li, Phys. Chem. Chem. Phys., 2013, 15, 7657 RSC.
- F. Yu, Z. Wang, S. Zhang, H. Ye, K. Kong, X. Gong, J. Hua and H. Tian, Adv. Funct. Mater., 2018, 28, 1804512 CrossRef.
- J. Xu, Y. Li and S. Peng, Int. J. Hydrogen Energy, 2015, 40, 353–362 CrossRef CAS.
- Q. Liu, J. Wang, D. Liu, R. Li and T. Peng, J. Power Sources, 2018, 396, 57–63 CrossRef CAS.
- Z. Cheng, W. Fang, T. Zhao, S. Fang, J. Bi, S. Liang, L. Li, Y. Yu and L. Wu, ACS Appl. Mater. Interfaces, 2018, 10, 41415–41421 CrossRef CAS.
Footnote |
| † These authors contribute equally to the work. |
| This journal is © The Royal Society of Chemistry 2024 |