Leveraging microtopography to pattern multi-oriented muscle actuators

Abstract

Engineering skeletal muscle tissue with precisely defined alignment is of significant importance for applications ranging from drug screening to biohybrid robotics. Aligning 2D contractile muscle monolayers, which are compatible with high-content imaging and can be deployed in planar soft robots, typically requires micropatterned cues. However, current protocols for integrating microscale topographical features in extracellular matrix hydrogels require expensive microfabrication equipment and multi-step procedures involving error-prone manual handling steps. To address this challenge, we present STAMP (simple templating of actuators via micro-topographical patterning), an easily accessible and cost-effective one-step method to pattern microtopography of various sizes and configurations on the surface of hydrogels using reusable 3D printed stamps. We demonstrate that STAMP enables precisely controlling the alignment of mouse and human skeletal muscle fibers without negatively impacting their maturation or function. To showcase the versatility of our technique, we designed a planar soft robot inspired by the iris, which leverages spatially segregated regions of concentric and radial muscle fibers to control pupil dilation. Optogenetic skeletal muscle fibers grown on a STAMPed iris substrates formed a multi-oriented actuator, and selective light stimulation of the radial and concentric fibers was used to control the function of the iris, including pupil constriction. Computational modeling of the biohybrid robot as an active bilayer matched experimental outcomes, showcasing the robustness of our STAMP method for designing, fabricating, and testing planar biohybrid robots capable of complex multi-DOF motion.

---

Introduction

Skeletal muscle is a key component of the locomotor system, enabling voluntary movement through force generation.^1,2 Engineered muscle tissues capable of producing measurable forces are valuable in vitro tools for screening new therapeutic strategies for neuromuscular pathologies.^3–9 Engineered skeletal muscle has also emerged as an excellent candidate actuator for soft “biohybrid” robotics, owing to its energy efficiency, adaptability, and the ability to precisely trigger contraction via electrical or optical stimulation.^10–14 An important consideration for all these applications is precisely patterning the alignment of multinucleated muscle fibers within engineered tissues.^15,16

In 3D engineered muscles, fiber alignment is typically achieved by tensioning the tissue between two posts, yielding global alignment of fibers parallel to the axis of imposed tension.^17–19 Deflection of the posts in response to muscle contraction has proven a useful method of monitoring tissue function in physiological and pathological states, as well as for converting tissue forces into useful robotic functions, such as walking and gripping.^20–23 With the rise of high-content imaging, engineered contractile 2D muscle monolayers have been of increasing interest in the context of drug screening, as they enable rapid and scalable monitoring of tissue morphology and function.^5,7,24,25 Precision alignment and compatibility with live cell imaging is particularly important in this application, as random alignment of muscle fibers may result in contractile forces and dynamics that are not directly comparable between biological replicates, thus rendering it difficult to make clear distinctions between healthy, diseased, and treated tissues.²⁶ Patterning contractile 2D skeletal muscle is also interesting for biohybrid robotics, as it would enable deploying biological actuators in planar formats that enable multi-degree-of-freedom motions such as twisting, coiling, and swimming that have been accomplished with 2D cardiac muscle.^27–31 However, accomplishing this goal requires the ability to pattern skeletal muscle monolayers that replicate the complex multi-oriented alignment geometries observed in native tissue, such as multipennate and circular muscles, and can be sustained in culture over several weeks.

For many years, 2D skeletal muscle monolayers were not considered useful or robust for real-world applications, as they delaminate from rigid substrates within a few days of differentiation, thus preventing long-term monitoring of morphology and contractile function.^32,33 Early efforts to pattern adhesion-promoting proteins such as fibronectin, gelatin, and Matrigel on stiff plastic/glass substrates using microfabricated stamps proved successful at aligning skeletal muscle fibers over a few days in culture,^32,34 but were not suitable for maintaining contractile monolayers over several weeks or months. As an alternative, several studies reported that muscle monolayers could be maintained for longer time periods on rigid microfabricated scaffolds coated with adhesion-promoting biopolymers if the scaffolds contained 3D microtopography, i.e. aligned grooves. While effective, these methods typically rely on complex multi-step protocols that require microfabrication facilities, and also use opaque materials such as silicon wafers as 3D scaffold materials which impairs live cell microscopy.^35–37 Moreover, such rigid materials are not suitable scaffolds for planar soft robots which typically require compliant biocompatible polymers such as poly (dimethyl siloxane) and gelatin methacrylate to demonstrate large deformations in response to muscle actuation.^28,38

We have previously shown that 2D muscle monolayers grown on compliant and translucent fibrin hydrogels, which better recapitulate the soft and viscoelastic mechanical properties of native tissue,³⁹ can be maintained in culture for several weeks in culture while enabling live cell microscopy.⁴⁰ However, these muscle tissues were not globally aligned, necessitating approaches to facilitate alignment by patterning grooves directly in soft extracellular matrix-mimicking hydrogels such as fibrin. Hydrogel micro-molding typically requires tedious fabrication protocols comprising error-prone manual handling steps (e.g. manually transferring and flipping over a layer of aligned muscle into a new culture dish⁴¹), or access to expensive microfabrication equipment that are limited to photosensitive hydrogels,⁴² which limits the range of materials that can be used as well as the accessibility of the technique. To address these issues, we developed a cost-effective, readily accessible, and one-step extracellular matrix molding approach to generate sheets of precisely aligned, contractile muscle in a variety of culture formats and from different cell sources.

Our robust and reproducible method, termed “simple templating of actuators via micro-topographical patterning” (STAMP), uses 3D printed stamps to patterning microscopic grooves into natural hydrogels cast in any format, including standard multi-well plates. We have designed and optimized a gel loading and mold release strategy to enable high-fidelity patterning of micro-topographical cues. Moreover, we show that a simple ultrasonication cleaning strategy can be deployed to enable sustainable re-use of stamps over multiple cycles. Leveraging STAMP, we investigated how micro-topographical patterning impacted muscle alignment efficiency, fiber morphology, and contractile function in both mouse and human myoblasts.

As a showcase of the versatility of our method, we leveraged STAMP to pattern complex multi-degree-of-freedom motion in a planar muscle actuator. Given the difficulty of patterning muscle fiber alignment in multi-oriented geometries, biohybrid robots have thus far relied on proof-of-concept demonstrations of robots that walk, grip, or swim in response to one degree-of-freedom (DOF) motion from unidirectionally aligned 3D muscle tissues.^{21–23,42,43} The ability to simply, efficiently, and precisely pattern the alignment of contractile muscle fibers in any spatial geometry via STAMP, while retaining their force-generation capacity, opens up the possibility of designing multi-oriented architectures capable of multi-DOF motion. We thus fabricated a fibrin layer patterned with a series of concentric and radial microgrooves arranged around a circular hole, mimicking the native architecture of the iris muscles that control pupil dilation in the eye. Optogenetic mouse muscle cells seeded on this substrate were differentiated in a multi-DOF muscle configuration. Stimulation of the iris was used to control pupil constriction by selectively shining light on the concentric region. Experimental results matched computational predictions, indicating significant future potential in designing and deploying planar biohybrid robots capable of complex multi-DOF motion.

Beyond robotics, we anticipate STAMP will provide the tissue engineering community with a rapid, accessible, cost-efficient, and versatile way of introducing microscale topographical cues in ECM hydrogels without the need for complex multi-step microfabrication methodologies.

Results

Simple templating of actuators via micro-topographical patterning (STAMP)

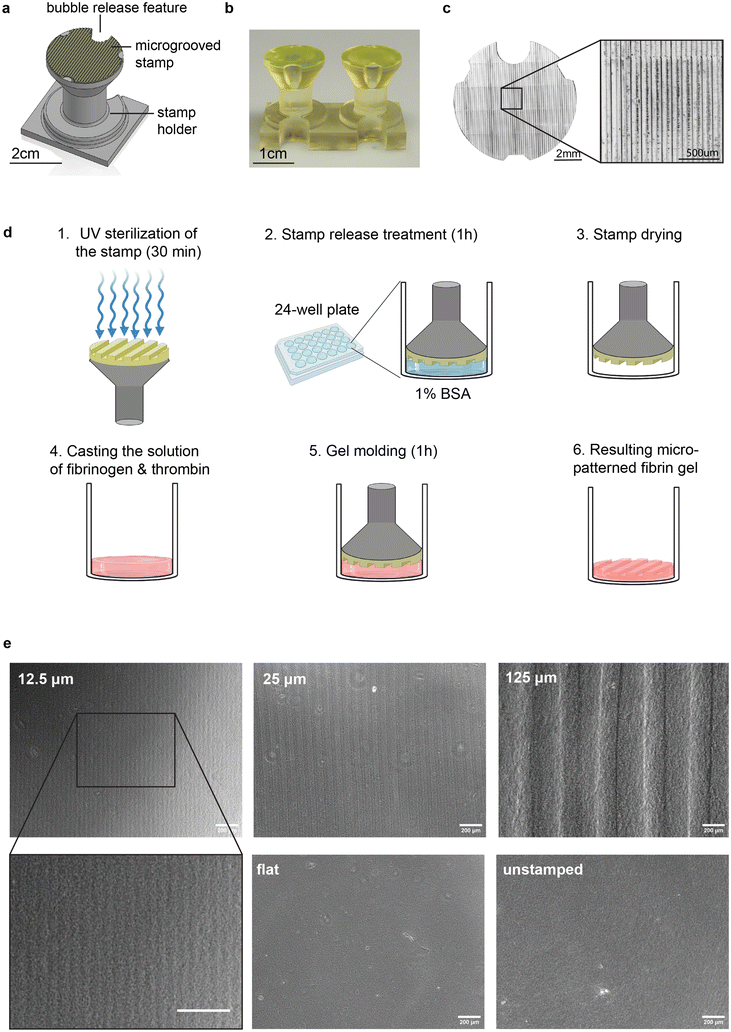
To generate aligned muscle tissues in a fast and versatile manner, and explore the impact of groove size and cell source on tissue morphology and function, we developed a one-step hydrogel molding protocol that can be applied to a variety of cell culture formats, such as multi-well plates and microfluidic chips as well as a range of hydrogel crosslinking chemistries. Specifically, we 3D printed stamps that fit in commercially available 24-well plates and used them to pattern vertically aligned (90°) microgrooves into hydrogels cast in each well. Stamps were attached to a holder with an integrated “bubble release” feature to prevent formation of defects commonly seen in molding viscous pre-crosslinked hydrogels (Fig. 1a–c and ESI Fig. 1†). We printed the holders as pairs connected by a rigid beam (Fig. 1b) to facilitate reproducible vertical alignment of microgrooves with respect to the multi-well plate. Stamps were UV-sterilized and immersed in a 1% bovine serum albumin solution for 1 hour to facilitate subsequent mold release.⁴⁴ Stamps were dried prior to use.

Fig. 1 STAMP, a simple and versatile method to fabricate micro-grooved hydrogel substrates. (a) Computer-assisted design (CAD) model of the micropatterned stamp and holder and (b and c) resulting 3D-printed parts. (d) Schematic steps of the stamp treatment and hydrogel patterning processes (created with biorender.com). (e) Brightfield microscopy pictures of fibrin gels harboring grooves of different sizes (equal width and depth), patterned with a non-grooved stamp (‘flat’), or not stamped at all.

To fabricated micro-grooved hydrogels, we cast a liquid solution of fibrinogen monomer (8 mg mL⁻¹) and thrombin crosslinker (100 U mL⁻¹) into each well of a 24-well plate, given widespread use of fibrin as a substrate for skeletal muscle culture.^45–47 Specifically, we followed our previously established protocols for generating fibrin with rheological properties that sustain longitudinal culture of skeletal muscle monolayers over several weeks.⁴⁰ Immediately after casting the liquid prepolymer solution, we placed the stamps into the wells and incubated the setup for 1 hour at 37 °C in a cell culture incubator to enable polymerization into a crosslinked fibrin hydrogel. Finally, we removed the stamps from the wells, showcasing efficient transfer of microgrooves onto the surface of the hydrogel (Fig. 1d). The features of the pattern, such as the depth and width of the grooves, can be easily varied by modifying the computer-assisted design (CAD) model of the stamp (Fig. 1e). Furthermore, stamps can be reused after a quick cleaning protocol comprising rinsing, sonication and UV sterilization (Methods and ESI Fig. 2†). Overall, our method offers a rapid and versatile way to engineer the microscale topography of translucent and mechanically compliant hydrogels used as cell culture substrates. Moreover, a simple redesign of the stamp can be used to pattern aligned muscle in other culture formats, such as microfluidic devices (ESI Fig. 3†).

To explore whether and how the interplay between cell size and groove size influences muscle alignment, we printed stamps with groove dimensions (equal depth and width) of 1×, 2×, and 10× the size of single muscle cells of mouse (C2C12, ATCC) and human (skMDC, Cook Myosite) origin (Fig. 1e, 2a, b and ESI Fig. 4†), namely 12.5, 25, and 125 μm. We also printed a flat stamp devoid of microgrooves to verify that potential differences in cellular orientation were not a result of the gel stamping or mold-release coating process. We included unstamped fibrin gels in our study as an additional control.

Fig. 2 Effect of micro-grooved fibrin substrates on the orientation of muscle cells. (a) Mouse and human myoblasts upon seeding on a fibrin scaffold containing 25 μm-wide grooves. Scale bar: 200 μm. (b) Diameter of single mouse and human myoblasts in suspension. ns: non-significant difference according to the Mann–Whitney–Wilcoxon two-sided test (p = 0.63). Mouse: n = 75; human: n = 127. (c and d) Representative full-well images of mouse and human muscle fibers after 12 days of differentiation on fibrin substrates with different sizes of grooves, and on non-patterned controls. Magenta: myosin heavy chain. Scale bar: 1 mm. (e and f) Distribution of mouse and human muscle fiber orientation on micro-grooved or control substrates. The different colors represent different replicates. (g) Proportion of muscle fibers aligned within ±20° of the mean of the distribution. Statistical significance: *: 10⁻² < p ≤ 5 × 10⁻², **: 10⁻³ < p ≤ 10⁻², ***: 10⁻⁴ < p ≤ 10⁻³, ****: p ≤ 10⁻⁴. Test: ANOVA followed by Tukey's HSD post hoc test.

Characterization of STAMPed hydrogels

To visualize the 3D architecture of STAMPed grooves, we stained the gels with an anti-fibrinogen antibody and acquired Z-stack confocal images (ESI Fig. 5a†). The XZ projection of the stacks provides information about the depth of the grooves. While gels STAMPed with small grooves (12.5 μm and 25 μm) appear symmetrical in width and depth, as designed, gels stamped with larger grooves (125 μm) appear shallower than originally designed. Gels in all grooved conditions demonstrated clear periodicity, demonstrating the efficacy of the STAMPing process (ESI Fig. 5b†). We also investigated the impact of STAMPing on the gels’ nanoscale architecture through scanning electron microscopy (SEM), enabling visualization of hydrogel fibrils across different groove sizes and controls (ESI Fig. 5c†). Notably, STAMP did not seem to influence the global orientation of individual fibrils within the hydrogels, but did seem to reduce the hydrogel pore size as compared to unstamped controls (ESI Fig. 5c and d†). Unstamped controls thus displayed a visually rougher surface than STAMPed gels, both in the presence and absence of grooves (ESI Fig. 5e†). STAMPed gels also harbored minor defects, potentially arising from the forces exerted on the gel surface during stamp release. Overall, there is evidence that STAMP alters hydrogel architecture at the subcellular scale, motivating further investigation of how muscles cells of mouse and human origin align, mature, and contract on STAMPed and unstamped substrates.

STAMP efficiently aligns mouse and human myoblasts

Different variants of stamps were used to pattern fibrin hydrogels as described above, in triplicates, prior to seeding with either mouse or human myoblasts (Fig. 2a). After 1–2 days in growth medium, the cells reached confluency and were transitioned to a differentiation medium, following previously optimized protocols.⁴⁶ We changed the medium daily to promote fusion into multinucleated fibers and preserve cell viability and metabolic activity. Fused muscle fibers were visible in all conditions. Muscles were differentiated until day 12, and then fixed and stained with an antibody against myosin heavy chain. A point-scanning confocal microscope was used to record and stitch together images of the full well for each condition (Fig. 2c and d), which were then used to quantify the distribution of muscle fiber orientations (Fig. 2e and f). Measuring the orientation at the scale of the whole well (cm-scale) allowed us to account for potential biases that could arise from local alignment of muscle fibers, which is commonly observed on soft hydrogels.⁴⁰ Irrespective of their species of origin, muscle fibers grown in grooved gels mainly aligned along the groove axis, while the orientations of muscle fibers grown on flat and unstamped gels were more variable (Fig. 2c–f). To quantitatively verify that micro-grooved substrates enabled precisely controlling the alignment of muscle fibers, we measured the proportion of fibers whose orientation fell within ±20° of the mean of the distribution of orientations (Fig. 2g). For both mouse and human cells, the proportion of uniformly oriented cells was significantly higher in grooved samples than in the non-patterned ones, irrespective of groove size. No significant difference in fiber alignment was found between the different groove sizes, and neither flat nor unstamped gels resulted in tissues that were as aligned as grooved samples. Taken together, these results indicate that our one-step method enables simple templating of actuators via micro-topographical patterning (STAMP) at the cm-scale.

Effect of STAMP on muscle contraction

Since the forces generated during muscle contraction are an important feature for functional characterization of engineered tissues for applications in high-throughput drug screening and robotics alike, we explored whether and how muscle function could be impacted by the micro-topography of the grooved hydrogel substrate. A function generator connected to a custom 24-well plate lid with integrated platinum electrodes was used to stimulate mouse and human muscle tissues grown on STAMPed and unstamped fibrin following previously established protocols for electrical stimulation.⁴⁸ Brightfield microscopy videos of muscle contraction were recorded in response to electrical stimulation at 1 Hz and 4 Hz (ESI Videos 1–10†).

Using a custom open-source computer vision pipeline,^26,49,50 we tracked the displacement of stimulated tissues with high 2D spatiotemporal resolution. We also calculated the displacement vectors between a contraction peak and the preceding relaxation phase, enabling spatial visualization of dynamic muscle contraction as vector fields (Fig. 3a). Since muscle fibers generate force along their long axis, substrates with vertically aligned grooves appeared to yield tissues that twitched in a more uniformly vertical direction than non-patterned substrates. We quantified contraction direction by calculating the ratio of Y-displacement to X-displacement during muscle contraction (Fig. 3b). While STAMPed gels appeared to have higher average Y/X displacement ratios as compared to flat and unstamped controls, these results were not statistically significant except when murine samples were pooled together in two groups (grooved and non-patterned, ESI Fig. 6†). Interestingly, the Y/X displacement ratio for muscle fibers grown on 12.5 μm grooves significantly differed from the theoretical mean of 1 (i.e. equal X and Y displacement) for both species. As will be examined further in the discussion, we attribute the lack of statistical significance for other groove sizes to the relatively small imaging window (mm-scale) compared the total size of the tissue (cm-scale).

Fig. 3 Impact of microscale topographical cues on muscle contraction. (a) Spatial maps of displacement vectors generated by mouse and human cells upon electrical stimulation, after 12 days of differentiation. Cells were either grown on substrates with microscopic grooves or non-patterned controls. (b) Quantification of the ratio between muscle displacement in the y and x directions. First, the mean y- and x-displacement profiles for the whole video were plotted. Then, the ratio was computed from the maximum of each profile. for both species, while no significant differences were found between the different conditions with the Kruskal–Wallis test (p = 0.057 for mouse, p = 0.282 for human), cells grown in 12.5 μm grooves had a y/x ratio that significantly differed from 1, denoted by a dotted line on the plots (mouse: p = 0.047, human: p = 0.007, Wilcoxon signed-rank test). (c) Maximal height of the peaks from the mean absolute displacement profiles generated by muscle fibers upon electrical stimulation. Microtopography did not significantly impact contraction magnitude for either species.

As the total displacement that a contractile muscle layer generates is dependent on the direction and timing at which individual fibers contract, we also calculated the mean absolute displacement (MAD) from each video and plotted the largest displacement between a peak and the next valley (Fig. 3c). The presence of grooves did not significantly impact the twitch magnitude upon electrical stimulation, or the contraction kinetics (time to peak force, time at peak force, relaxation time, ESI Fig. 7†), irrespective of groove size and species of origin. These results indicate that STAMP enables efficiently aligning contractile 2D muscle on substrates that promote monolayer longevity without negatively impacting the strength of the differentiated tissue.

Effect of STAMP on muscle maturation and fiber morphology

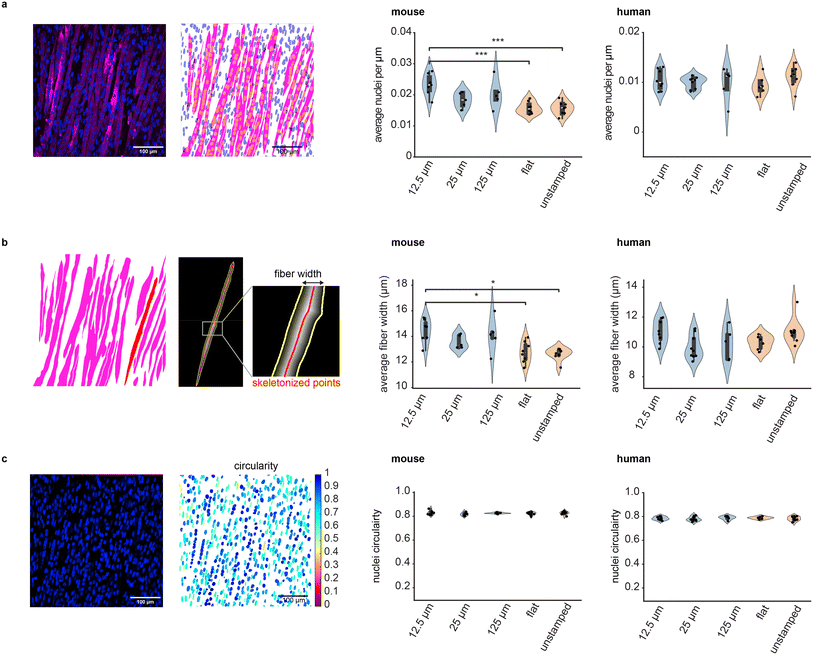
We explored the effect of STAMP on muscle maturation by quantifying the width of muscle fibers, their fusion index (a measure of how many nuclei are contained within each muscle fiber on average), and nuclei circularity across conditions (Fig. 4). Differentiated muscle tissues were stained with myosin heavy chain to visualize muscle fibers (MF20 for mouse and anti-MYH2 for human) and NucBlue to visualize nuclei, and imaged at high magnification via confocal microscopy.

Fig. 4 Impact of microscale topographical cues on muscle morphology and maturation. (a) Representative images (stained and processed) and quantification of the number of nuclei per unit length of muscle fiber for mouse and human cells grown on grooved or non-patterned substrates. Mouse muscle fibers grown on fibrin with 12.5 μm grooves harbored significantly more nuclei per micron than on flat (p = 2.80 × 10⁻⁴) or unstamped (p = 2.36 × 10⁻⁴) substrates (ANOVA followed by Tukey's HSD post hoc test). (b) Width of mouse and human muscle fibers grown on grooved substrates or non-patterned controls. Mouse muscle fibers grown on fibrin with 12.5 μm grooves were significantly wider than those grown on flat (p = 3.8536 × 10⁻²) or unstamped (p = 1.09 × 10⁻²) gels (Kruskal–Wallis followed by Dunn's post hoc test with Bonferroni correction). (c) Nuclei circularity measurement (1: perfectly circular) for mouse and human cells on grooved or non-patterned substrates. Immunofluorescence pictures display myosin heavy chain in magenta and nuclei in blue, and 100 μm scale bars. For panels (a–c): statistical significance: *: 10⁻² < p ≤ 5 × 10⁻², **: 10⁻³ < p ≤ 10⁻², ***: 10⁻⁴ < p ≤ 10⁻³, ****: p ≤ 10⁻⁴.

Fusion index was calculated by segmenting muscle fibers and nuclei and quantifying how many nuclei were contained per unit length of a given muscle fiber. We measured similar fusion indices for human cells in all experimental conditions, and for mouse cells in most experimental conditions, though mouse muscle tissues differentiated on 12.5 μm grooves contained significantly more nuclei per fiber length as compared to flat and unstamped samples (Fig. 4a). We also quantified the width of muscle fibers by skeletonizing each segmented fiber (i.e. reducing it to a single line preserving the overall fiber orientation, as shown in Fig. 4b) and measuring the shortest distance between each point of the skeleton and the edges of the fiber as detected by myosin heavy chain staining. Fiber width appeared uniform across all human samples and most mouse samples, though mouse muscle differentiated on 12.5 μm grooves were, on average, wider than flat and unstamped controls. Of note, while mouse and human myoblasts had similar sizes upon trypsinization from their expansion flasks, differentiated mouse muscle fibers tend to be larger than their human counterparts (ESI Fig. 8†). Finally, we also quantified the circularity of nuclei, a metric commonly used to characterize the efficacy of myoblast fusion into multinucleated fibers. This parameter was not significantly influenced by substrate microtopography for either species (Fig. 4c).

These results indicate that muscle fibers mature equivalently well on STAMPed and unstamped fibrin, and are even improved in some cases by the use of STAMPed substrates. Combined with our other data showcasing significantly improved global alignment in STAMPed muscles, these results suggest that our one-step molding approach is suitable for patterning complex multi-oriented tissue architectures at the cm-scale, as required for muscle actuators in soft robotics.

Deploying STAMP to generate multi-oriented muscle actuators for planar soft robots

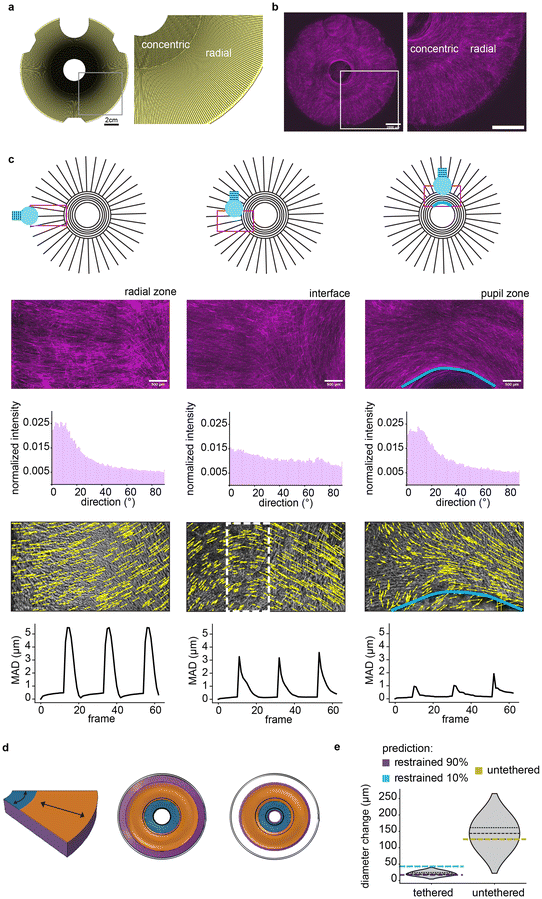
To demonstrate the versatility of STAMP for 2D spatial patterning of cells on hydrogels, we designed and manufactured a planar soft robot actuated by a multi-oriented muscle tissue. Our robot was inspired by the architecture of the iris, in which a region of muscle circumferentially aligned around a pupil is surrounded by a region of radially aligned muscle.⁵¹ We computationally modeled our tissues as a bilayer composed of a thick fibrin hydrogel overlaid with a thin muscle monolayer, in which the muscle was represented by a thermal material with an expansion coefficient matching the strain generated by our engineered mouse muscle tissues on 25 μm grooves (∼6.7% at 1 Hz). This modeling setup enabled mimicking the spatially distributed forces generated by a muscle monolayer composed of thousands of individually contracting fibers. Since the degree to which the gel adheres to the edges of the well plate is difficult to estimate, we modeled different scenarios with varying percentages of restraint against the edges of the well.

Alongside the computational model, we designed a stamp of the same geometry, comprising a central region of 25 μm concentric grooves surrounded by an outer region of 25 μm radial grooves (Fig. 5a). Similar to our multi-well plate patterning approach, we included a bubble release-feature to minimize structural defects arising from air trapped below the stamp. We then used the iris stamp to transfer the multi-oriented pattern onto a fibrin gel, as described and optimized above. STAMPed iris substrates were seeded with mouse myoblasts expressing the blue light-sensitive calcium ion channel channelrhodopsin2, conjugated to a TdTomato fluorescent tag.²¹ Upon differentiation, the cells formed muscle fibers that were precisely aligned to match the multi-oriented arrangement of the grooves, thereby mimicking the architecture of iris musculature (Fig. 5b).

Fig. 5 Leveraging hydrogel stamping to fabricate multi-oriented living actuators. (a) CAD design of a micro-grooved stamp mimicking the multi-layered ring architecture of iris muscles. Groove size: 25 μm. Scale bar: 2 cm. (b) Mouse C2C12 cells growing on a fibrin substrate stamped with the iris-like pattern from panel (a). Magenta: channelrhodopsin-TdTomato. Scale bar: 2 mm. (c) Schematic view of different regions of the iris, along with representative fluorescence images, directionality histograms, spatial maps of displacement vectors due to optically-stimulated muscle contraction at different locations of the well, and the corresponding mean absolute displacement signal (MAD). Regions of interest are symbolized by the red rectangle in the schematics, while the dashed white box indicates a transition zone where twitch direction shifts between the radial and concentric muscle layers. The outline of the pupil hole is shown in blue. The light bulb icon indicates the approximate position of the blue led used for optogenetic stimulation. Scale bars: 500 μm. (d) Left: 3D section of computational model of iris showing spatially segregated regions of concentric (blue) and radial (orange) aligned muscle monolayers on fibrin (purple). Model predicted displacement of the iris from its original configuration (denoted with black lines) is smaller in tethered (middle) than untethered configurations (right). (e) Experimentally observed pupil diameter change in tethered and untethered irises (violin plots) as compared to computational model predictions (colored dashed lines). For tethered tissues, the model incorporated cases in which 10% or 90% of the fibrin gel height adhered to the edges of the well.

Leveraging a custom fiber optic setup, we selectively stimulated different regions of the engineered iris with blue light (470 nm) to specifically trigger muscle contraction in only that region while recording brightfield microscopy videos (ESI Videos 11–13†). Tracking data from our custom computational framework was used to plot spatial maps of the displacement generated by muscular contraction, as described above (Fig. 5c). These analyses demonstrated that local displacement generally followed the direction of muscle fibers in that region, while highlighting transition zones at the interface between differently oriented regions.

When STAMPed irises were tethered to the underlying well plate, we observed slight shrinkage of the pupil diameter in response to contraction of the multi-oriented actuator (21.40 ± 5.53 μm), mimicking the function of native iris musculature. As biohybrid robots are often deployed in an “untethered” format to minimize resistance to contraction and maximize actuator stroke,^42,52 we released the STAMPed iris from the well plate and showcased a corresponding increase in the pupil shrinkage in response to light-triggered muscle contraction (143.62 ± 35.12 μm, ESI Video 14†). Empirical results validated computational modeling of STAMPed irises in both tethered and untethered configurations (Fig. 5d and e). Of note, the close match between the measured pupil shrinkage in the tethered iris and the model prediction with 90% restraint suggests a strong adhesion between the gel and the edges of the well wall. Overall, these results showcase the robustness of STAMP for designing, fabricating, and testing planar biohybrid robots capable of complex multi-DOF motion.

Discussion and conclusion

We have developed STAMP, a one-step protocol for integrating microscale topography in extracellular matrix hydrogels, and demonstrated its ability to rapidly and precisely pattern skeletal muscle monolayers in a range of geometries at the cm-scale. Our method is compatible with a wide range of cross-linkable hydrogels as well as live cell microscopy, enabling high-throughput morphological and functional characterization of tissues. In addition, it can be readily adapted to complex patterns beyond simple linear alignment, as demonstrated by the fabrication of a multi-oriented iris-mimicking bioactuator.

As compared to previous approaches of coating 3D micro-grooved scaffolds with extracellular matrix hydrogels, our method of generating aligned 2D muscle does not require complex multi-step microfabrication procedures, and is also compatible with live cell imaging and untethered deployment in soft robots.^35–37 Of note, there are other effective 2D muscle alignment strategies that are compatible with high-throughput imaging and longitudinal monitoring, such as growing myoblasts on electrospun nanofibers coated with adhesion-promoting biopolymers such as Matrigel.^5,25 However, electrospinning requires custom experimental setups that are challenging to spatially control, thus providing limited precision over the 2D patterning of nanofibers. This limitation largely restricts electrospun substrates to fabricating unidirectionally aligned muscle layers which are suitable for high-throughput therapeutic screening (though not broadly accessible in all lab environments) but cannot be readily adapted to generate the multi-oriented architectures required for biohybrid robotics.

While others have also successfully patterned microgrooves into hydrogel scaffolds,^41,42,53 these protocols involve long, multi-step manufacturing processes, and rely on complex microfabrication tools that are not always readily available in resource-limited research institutions. In our study, we used a 3D printer to explore the effect of various groove sizes on muscle fiber orientation, and our analyses revealed that grooves as wide as 125 μm enabled reliable fabrication of aligned muscle tissues from both mouse and human cell sources. This size is well within the print resolution of commercial stereolithographic 3D printers (SLA), and several companies even offer the printing and shipping of SLA-printed parts as a service, should the cost of owning a printer be excessive in resource-limited settings. To facilitate open access and reproducibility of our method, stamp designs can also be virtually uploaded and readily shared between groups (see ESI† for all our CAD files). Moreover, our simple optimized cleaning protocol facilitates mold reuse over multiple cycles, further increasing the cost- and time-effectiveness of STAMP. One downside of our protocol is the dependence of pattern quality on uniform contact between the gel surface and the stamp grooves. This requires careful optimization of the gel volume and holder length when adapting STAMP to new cell culture formats, such as multi-well plates of different sizes or microfluidic chips (ESI Fig. 3†).

While we found that groove size did not significantly affect muscle fiber alignment in either our mouse or human cell-derived tissues, it is important to note that other researchers have identified “optimal” dimensions of microscale grooves^37,53 or micropatterned ligands³² that can control the orientation of skeletal muscle tissue. These dimensions, however, vary across studies, ranging from less than 2 μm to 100 μm, suggesting that differences in the substrate fabrication process or in the quantification of alignment might influence the reported results.^36,53–56 One explanation for this phenomenon is that most prior studies analyze alignment at a local scale (i.e. tissue sub-region spanning hundreds of microns), whereas we assess tissue-wide alignment at the cm-scale. Thus, our analyses may have disregarded subtle off-pattern angling sometimes reported for muscle fibers grown in wider grooves or ligand patterns.^32,53 While these microscopic differences may be interesting to study, we consider global tissue alignment and coordinated contraction to be more useful metrics for both high-throughput drug screening and macroscopic biohybrid robots. Importantly, given our results with flat-stamped substrates, we do recognize there is a maximal groove width beyond which no muscle alignment would be observed. However, our results show that microgroove widths up to 125 μm are sufficient to coordinate the interplay of physical confinement and asymmetric cellular elongation required for efficient alignment of both mouse and human muscle. Future studies will be necessary to determine the roles of seeding density and growth rate, which must also influence the physical confinement of single cells.

Unlike groove width, the impact of groove depth on muscle orientation is rarely investigated. A recent study explored this aspect of substrate topography by fabricating silicon substrates for muscle with grooves of ‘touchable’ and ‘untouchable’ depths.³⁵ They found that muscle fibers were unable to span gaps with untouchable depths (∼400 μm, >30× the size of single myoblasts in suspension), which forced them to grow along the edges of the topological features. While we did not systematically probe the effect of groove depth in this study, we always observed confluent muscle monolayers on fibrin substrates, irrespective of microtopography. In other words, no groove depth we investigated was ‘untouchable’ for our cells. As fibrin swells upon liquid absorption, the edges of STAMPed grooves smoothen over time (ESI Fig. 5†), likely facilitating more uniform cellular proliferation as compared to previous studies on rigid etched silicon wafers. Notably, while the loss of groove shape fidelity is especially apparent in gels with larger grooves (125 μm), this did not seem to impact the ability to reliably align muscle tissues (Fig. 2), indicating this geometry is suitable to use if access to high resolution printers is an issue. Since we used stamps with equal width and depths to maintain equal aspect ratios in all conditions, additional investigations are needed to determine whether changing the grooves’ aspect ratio influences muscle morphology or function.

In our study, STAMP proved effective at aligning myoblasts from both human and mouse origin. However, a previous study has shown that mouse and human myoblasts responded differently to substrates displaying micropatterned ligands.³² In this alternate setup, C2C12 cells required a specific line spacing to align properly (20–30 μm), unlike primary human myoblasts, which the researchers imputed to inter-species differences, such as the higher growth rate and inherent orientation bias they observed with C2C12 cells. In our study, mouse and human cells displayed different fiber orientation distributions, with better-defined peaks and narrower tails for mouse alignment distributions (Fig. 2c–f). However, this difference could be due to noisier myosin staining for human cells, which impacted subsequent directionality analysis, rather than indicating inter-species variability. For both species, the presence of noise in the immunofluorescence images also lowered the proportion of fibers oriented within ±20° of the mean by introducing randomly oriented speckles. Regardless, the alignment of muscle fibers was significantly more uniform on STAMPed versus unstamped fibrin, irrespective of groove size or the species of cellular origin (Fig. 2g).

Our assessment of muscle differentiation via morphological metrics such as fusion index, fiber width, and circularity showed largely similar findings in mouse and human cells. For human muscle, there was no significant variation in all assessed metrics irrespective of experimental conditions. While this was also true of most mouse samples, mouse muscles cultured on 12.5 μm grooves demonstrated increased fusion index and fiber width as compared to flat and unstamped controls. Other studies have also found that alignment can promote muscle fiber differentiation in certain conditions. For example, studies of C2C12 cells grown on grooved elastomeric thin films have shown an increase in fusion index and expression of differentiation markers as compared to flat thin films.³⁷ In our study, since an increase in fusion index and width was only observed in the 12.5 μm grooved condition for mouse muscle fibers, which are on average wider than human muscle fibers (ESI Fig. 8†), it is possible that future studies on smaller groove sizes may enable further increases in fusion index and fiber width for STAMPed muscles. Notably, the increases in fusion index and fiber width for 12.5 μm grooved mouse muscle tissues did not translate to significantly higher twitch forces (Fig. 3c).

Despite statistically significant improvements in global alignment (Fig. 2), the ratio of Y/X displacement was not significantly different in STAMPed and unstamped controls, though mouse and human muscles on 12.5 μm grooves demonstrated Y/X ratios significantly different from 1, indicating higher Y displacement (Fig. 3b). We attribute this observation to the relatively small field of view of recorded videos (∼1.7 mm × 1 mm) compared to the size of the full well (∼1.5 cm diameter for a 24-well plate). We and others have noted that skeletal muscle grown on compliant substrates will exert traction forces to align locally even in the absence of grooves.⁴⁰ As a result, even non-patterned samples will sometimes display fibers with near vertical alignment at the mm-length scale. By contrast, skeletal muscle grown on flat stiff substrates such as glass demonstrate much less local alignment and readily delaminate from substrates within a few days of differentiation (ESI Fig. 9†). Taken together, our data on muscle maturation and contractility on STAMPed versus unstamped substrates indicate that local alignment of fibers at the μm–mm scale (which happens spontaneously on soft substrates) is required to promote muscle differentiation by facilitating fusion of myoblasts, and global alignment of muscle fibers at the cm-scale (which requires micropatterned cues) is required to control macroscale motion. STAMP enables controlling both local and global alignment with high fidelity, highlighting it's potential for fabricating cm-scale soft robots.

STAMP's ability to reproducibly pattern cm-scale muscle with high-fidelity and high-resolution enabled us to design a planar soft robot capable of complex multi-DOF motion in response to muscle contraction. In previous demonstrations of biohybrid robots actuated by 3D skeletal muscle, the engineered bioactuator contained largely unidirectionally aligned fibers and was thus only capable of 1-DOF contraction. While these actuators have been sufficient to demonstrate proof-of-concept applications such as walking or pumping or swimming,¹¹ there remains a need to design and deploy engineered muscle actuators that reproduce more complex architectures and motion patterns as observed in native tissues. Likewise, while planar configurations for biohybrid robots have proven very impactful for machines powered by 2D sheets of cardiac muscle,^{27–31,38,57} there have been fewer demonstrations of skeletal muscle monolayers cultured on untethered 2D substrates,^58,59 likely due to the large passive and active tensions generated by muscle fibers that lead to cell delamination and substrate wrinkling. In this study, we leveraged fibrin as a substrate for a planar soft robot, as fibrin enables longitudinal 2D culture of skeletal muscle over several weeks without delamination or wrinkling.⁴⁰ Deploying STAMP to generate a complex micro-topographical pattern in fibrin yielded a multi-oriented muscle actuator capable of multi-DOF motion. We were able to mimic the architecture and actuation of an iris composed of optogenetic muscle, enabling complex behaviors such as regionally-specific force generation and light-controlled pupil constriction (Fig. 5).

In the future, we anticipate that STAMP can be readily adapted to a range of cell culture formats, such as well plates with different diameters, Petri dishes, or even microfluidic chips, simply by editing the design of the 3D printed parts (ESI Fig. 3†). Because STAMP is independent of hydrogel chemistry, it could also be used to pattern a variety of extracellular matrix-mimicking hydrogels suitable for different cell types such as collagen or gelatin methacrylate, as long as the crosslinking kinetics enable casting and stamping of the liquid prepolymer prior to sol–gel transition. Our demonstration of using STAMP to align cells of both mouse and human origin adds to published research showing that micro-grooved substrates enable controlling the orientation of various cell types. Beyond skeletal muscle and neuromuscular junctions,^54,60 microgrooves have also been shown to enhance the alignment of cardiomyocytes,⁶¹ neurons,^62,63 and periodontal ligament cells,⁶⁴ among other cell types. However, as STAMP does not enable precise positioning of single cells upon seeding, adaptation of the method towards cell types that require specific initial configurations (such as engineered neuron networks) will require combining with other existing methods for spatially controlling cell seeding.^65,66 We anticipate that the accessibility and reproducibility of our STAMP technique, combined with our method for predictive computational modeling of STAMPed muscles, will enable others in the field to design and deploy patterned muscle monolayers for diverse applications in disease modeling and soft robotics.

Methods

Stamp manufacturing

All the stamp holders described in this work were designed using a CAD software (Solidworks) and exported as .stl files to use with Formlab's Preform Slicer software. The stamp holders were printed out of surgical guide V1 resin without supports and with a layer height of 50 μm using a Formlabs 3B Stereolithography (SLA) printer (Formlabs). The stamps were post-processed in a form wash with isopropyl alcohol for 45 minutes and cured in a form cure UV curing chamber for 30 minutes at 70 °C as recommended by Formlab's Surgical Resin user guide.⁶⁷ The stamp holders were further cured at 80 °C in an oven for at least 20 hours to cure any remaining resin before combining them with UpPhoto micro-grooved stamps (described below). Just before attaching the micro-grooved stamps, the stamp holders were washed with soapy water, dried, and then run through a Tuttnauer benchtop line autoclave (Tuttnauer USA Co Ltd, 2840EL-D) at 121 °C using the preset plastic cycle and allowed to cool to room temperature.

Micro-grooved stamps (shown in Fig. 1a–c, Fig. 5a, and ESI Fig. 4†) were designed using Solidworks and exported as .stl files to use with UpNano's slicer software Think3D (UpNano GmbH). The flat stamps and the stamps with 125 μm feature sizes were printed using a 5× objective lens and UpPhoto Resin on a NanoOne 2-photon printer (UpNano GmbH). Stamps with smaller feature sizes of 12.5 μm and 25 μm including the 25 μm ocular stamps, were printed with UpPhoto resin on a 10× objective (UpNano GmbH). All stamp prints were post-processed by progressively soaking each print in 3 different isopropyl alcohol baths for 10 minutes each and then removing the prints from the build plate using a razor. All stamps were allowed to sit and further photo cure for at least 12 hours to remove any remaining uncured resin before attaching the UpPhoto micro-grooved stamps to the surgical V1 stamp holders described above.

The UpPhoto stamps were glued to the stamp holders using double-sided tape (9474LE 300LSE, 3M). To ensure proper fit of the tape to the stamp and holder, we cut the tape to the exact shape of the stamp using a Silhouette Cameo 5 electronic cutting machine (Silhouette). Each stamp was aligned using the port hole as a clocking feature in addition to kinematic pins and notches included in the design that assist in centering the stamps on the stamp holder. Stamps were sterilized under UV light in a biosafety cabinet for 30 minutes before each use. In addition, between each use, stamps were cleaned as described in the ‘stamp reuse’ section below.

Stamp and gel preparation

To facilitate subsequent release, the stamps were first soaked for 1 hour in bovine serum albumin (BSA, Thermo Fisher Scientific, 37525) diluted to 1% concentration. The linear stamps and ocular stamps were placed in 24-well plates (Avantor, 10891-558), each with 1.5 mL of BSA. After 1 hour, the stamps are removed from the BSA bath and allowed to dry to remove excess BSA. The fibrin gels were made at the same concentration as described in Bu et al.⁶⁸ We created a solution of 8 mg of fibrinogen from fetal bovine plasma (Sigma Aldrich, F8630-1G) per mL of pre-warmed (37 °C) Dubelco's modified Eagle's medium (DMEM) (Sigma Aldrich, D6429-500ML). We vortexed the solution to dissolve clumps and filtered the solution using a Nalgene® Rapid-Flow™ Vacuum Filter Unit with 0.20 μm pore size (Avantor Sciences, 82030-938). We then added 0.4 μL of thrombin from bovine plasma (Sigma-Aldrich, T4648-1KU) to the mix to initiate polymerization. 500 μL of the mixture of fibrinogen and thrombin was then pipetted into each well of a 24-well plate (Cellvis, P24-1.5H-N) before stamps were added. The stamps were then placed into the wells, in contact with the gel, and the plate was lightly tapped and tilted to push any visible air bubbles trapped underneath the stamp towards the bubble-release feature. After loading and stamping, the platforms were kept at room temperature for 45 minutes. After incubation and polymerization, the stamps were carefully removed and the gels were kept hydrated with 0.5 mL of growth medium per well until they were seeded with cells.

Stamp reuse

After the stamps described in the “Introduction” section were used to pattern gels, they were cleaned by first rinsing and soaking them in water immediately after use. They were then sonicated for at least 20 minutes in a 70% ethanol bath and dried using lens cleaner paper to remove any gel residue from the microgrooves. The stamps were then sterilized under UV light in a biosafety cabinet for 30 minutes before reuse. Pictures of gels made with stamped used for the 4th time after being cleaned can be found in ESI Fig. 2.† We did not observe any significant difference between gels made with stamps used for the first time and those used for a fourth time after cleaning.

Hydrogel characterization through confocal microscopy

Fibrin hydrogels were blocked for an hour in 1% BSA (Thermo Fisher Scientific, 37525) and then incubated with a bovine fibrinogen polyclonal rabbit antibody (1 : 200) for 1 h (Thermofisher, BS-10361R). Hydrogels were then washed in PBS and incubated with the secondary antibody, Alexa Fluor 555 donkey anti-rabbit (1 : 500) for 1 h (Fisher Scientific, A31572). Samples were imaged on a Nikon AXR Confocal microscope with a 10× air objective. Z-Stacks were acquired and projected to display the XZ and YZ profiles of the gels. The intensity profile from the XZ projection was plotted in ImageJ Fiji.⁶⁹

Hydrogel characterization through confocal scanning electron microscopy

Electron microscopy imaging, consultation and services were performed in the HMS electron microscopy facility. Cell-free fibrin gels were rinsed 3 times for 5 min each time in 0.1 M sodium cacodylate buffer, pH 7.4, and then incubated for 1 hour with 1% osmiumtetroxide/1.5% potassiumferrocyanide in double distilled water, before rinsing again for 3 times 5 min in double distilled water. The samples were then dehydrated in a series of ethanol solutions as follows: 50% 5 min, 70% 5 min, 95% 10 min, 100% for 2 × 10 min. To preserve structures for SEM imaging, the samples were then dried with a critical point drier (Autosamdri®-931, Tousimis) using 4 one-hour stasis periods. They were mounted onto stubs and sputter coated with 6 nm platinum (Leica EM ACE600). Finally, samples were imaged with a Hitachi S-4700 FE-SEM at magnifications ranging from ∼300× to 3000×. Directionality profiles of each uncropped 3000× picture were plotted by applying the Directionality function from ImageJ Fiji.⁶⁹ This provides information about the orientation of hydrogel fibrils and other features, such as grooves and cracks. Additionally, we estimated the surface roughness of each sample. We started by plotting the intensity profile of N = 3 horizontal lines drawn in each 3000× image in ImageJ Fiji. We estimated surface roughness as the root mean square of the intensity profiles.⁷⁰

Cell culture

Mouse myoblasts C2C12 cells were used both for linear alignment studies (C2C12 WT cells, ECACC, 91031101-1VL) and for the multi-oriented iris-mimicking construct (optogenetic C2C12 cells expressing 470 blue light sensitive Channelrhodopsin [ChR2(H134R)] tagged with tdTomato).²¹ They were expanded in growth medium (GM) consisting of fetal bovine serum (1 : 10 vol/vol, Life Technologies, A5670701), Corning™ L-glutamine solution (1 : 100 vol/vol, Fisher Scientific Co LLC, MT25005CI), 0.25 μg ml⁻¹ amphotericin B (ThermoFisher, 15290026) and 1% penicillin–streptomycin (Fisher Scientific Co LLC, MT30002CI) dissolved in DMEM (Sigma Aldrich, D6429). The cells were seeded at a density of 100 000 cells per well of a 24-well plate and grown in growth medium (GM) with 6-aminocaproic acid (ACA) (Sigma-Aldrich, A2504-100G) at a ratio of 1 : 50 vol/vol for one day until they reached confluency. They were then switched to differentiation medium (DM) consisting of horse serum (1 : 10 vol/vol, Gibco, 26050-088), Corning™ L-glutamine solution (1:100 vol/vol, Fisher Scientific Co LLC, MT25005CI), 0.25 μg ml⁻¹ amphotericin B (ThermoFisher, 15290026) and 1% penicillin–streptomycin (Fisher Scientific Co LLC, MT30002CI) in DMEM (Sigma Aldrich, D6429), supplemented with inuslin-like growth factor-1 (IGF-1) (1 : 20 000 vol/vol, PeproTech, 100-11R3-1MG) and ACA as described above. The cells were allowed to differentiate for 12 days with media replacement every other day before being electrically stimulated, fixed, and stained, as described below.

Passage 1 human skeletal muscle myoblasts (skMDC) (Cook Myosite, #SK-1111-P01547-29M) were seeded on hydrogels at a density of 100 000 cells per 24-well plate. The skMDC cells were grown in growth media consisting of MyoTonic basal medium (Cook Myosite, MB-2222) and MyoTonic growth supplement (Cook Myosite, MB-3333) supplemented with 1% penicillin–streptomycin and 0.25 μg ml⁻¹ amphotericin. After 1 day the cells were switched to differentiation media consisting of KSR/CHIR/TGFbi/prednisolone [KCTiP] as described elsewhere⁷¹ supplemented with 0.2% penicillin–streptomycin, 0.25 μg ml⁻¹ amphotericin and 2% ACA.

On the 12th day after switching to differentiation media, the cells were electrically stimulated, fixed and stained as described below.

Electrical stimulation

Electrical stimulation was carried out by placing the cultures in 2 mL of DMEM and then supplying a 10 Vpp 20% duty cycle square wave using a Siglent SDG1032X function generator connected to electrodes made of platinum wires (Thermo Fisher Scientific, 010286.BY) suspended approximately 7 mm apart and 10 mm above the bottom of the well plate. To quantify the direction of twitch in C2C12 cultures, a frequency of 4 Hz was chosen in order to overcome the substantial and uneven spontaneous twitch exhibited by these cells on day 12. For skMDC cells, 1 Hz was used throughout the whole experiment. Thus, to ensure a fair comparison of peak heights between C2C12 and skMDC cells, we used 1 Hz for both cell sources when we quantified the maximal peak height. Twitch response was monitored with a brightfield Zeiss Primovert microscope equipped with an Axiocam 202 mono camera (Zeiss). Videos of muscle contraction were recorded at 30 frames per second at the center of each well in between the two electrodes, and 3 seconds were extracted from each video to quantify displacement magnitude and direction, as described below.

Optical stimulation

The optogenetic C2C12 cells used for the iris cultures were stimulated with both the same electrical setup described above and optically using 1 Hz blue light stimulation with a 20% duty cycle through a 470 nm optical fiber (Thorlabs), powered by an Agilent E3630A power supply (Agilent Technologies). Videos of muscle contraction in response to optical stimulation were acquired at 30 frames per second with a Zeiss Primovert Microscope.

Video tracking and analysis

Spatial maps of displacement were generated using a freely available tracking algorithm as described in previous studies.^26,49,50 Among other features, this code returns the X and Y positions of the automatically-identified tracking features over the whole duration of the video, along with their mean absolute displacement (MAD) in each frame. From these results, we calculated and plotted various functional metrics of tissue contraction in Jupyter Notebooks⁷² using the following packages: NumPy,⁷³ SciPy,⁷⁴ Pandas,⁷⁵ Matplotlib,⁷⁶ Seaborn,⁷⁷ cv2.⁷⁸ The maximal peak height was obtained by identifying the peaks and valleys of the MAD signal (using ‘scipy.signal.find_peaks’) and identifying the maximal difference between a peak and the following valley. To calculate the Y over X displacement ratio, we extracted the mean X displacement (MXD) and mean Y displacement (MYD) from all the X and Y positions tracking features for each 3-second video. We then divided the maximum of the MYD signal by the maximum of the MXD profile. To generate spatial maps of displacement vectors, we used the X and Y positions of tracking features extracted from video frames corresponding to one valley of the MAD signal and the peak immediately following it. Because of the large number of tracking features, we downsampled each position vector by a factor 25. We calculated the X and Y displacement vectors by subtracting the X and Y positions of the initial time frame from the corresponding positions in the final time frame. We then used a combination of matplotlib.pyplot's function ‘quiver’ and cv2's ‘imshow’ to display the displacement vectors overlaid with a brightfield image of the muscle fibers that generated this displacement. Note that, to emphasize the bi-directional nature of muscular contraction and relaxation, we plotted each vector in both its positive and negative direction, which resulted in double-sided arrows.

Muscle immunohistochemical staining and fluorescence imaging

After stimulation, electrical or optical, cells were fixed by soaking cultures in 4% paraformaldehyde solution (Avantor, 100503-917) dissolved in phosphate-buffered saline (PBS) (Thermo Fisher Scientific, 20012027) for 15 minutes. The paraformaldehyde was then washed away with three rinses of PBS. Tissues were then permeabilized using 0.5% Triton X-100 (Sigma Aldritch, T8787-50ML) for 20 minutes followed by three 5-minute PBS washes. Cultures were then blocked with 1% bovine serum albumin in PBS for 45 minutes. The muscle tissue cultures were then incubated with antibodies. Mouse cells were stained with either 1 : 100 myosin4 antibody conjugated to eFluor™ 660 (Invitrogen, 50-6503-82) for 1 h. Human cells were incubated with 1 : 200 mouse MYH2 monoclonal antibody (1F1B6, Thermo Fisher Scientific, 66212-1-IG) for 1 h, followed by 1 : 200 goat anti mouse Alexa Fluor 660 (Fisher Scientific, A21055). Cultures were then washed with PBS three times and stained with NucBlue (Thermo Fisher Scientific, R37605) for 15 minutes following the manufacturer's instructions. After one final round of three PBS washes, 3 drops of antifade media were added to each well. The C2C12 Channelrhodopsin2-expressing cultures constitutively expressed a TdTomato tag and were therefore not stained.

Following staining, all cultures were imaged using a Nikon AXR point scanning confocal microscope. To create the full-well images shown in Fig. 2 and 5, we stitched together maximum intensity projection images obtained from z-stack images acquired across the entire well using a 4× objective. To acquire higher magnification pictures, which involve objectives with lower working distances, we carefully extracted the fibrin gels (along with the fixed cells on top) from the 24 well plates using biopsy puncher and a spatula. We then flipped them over and transferred them to glass-bottom 6-well plates (Cellvis, P06-14-1.5-N) and imaged them with a 40× objective.

Image processing

Directionality distributions were calculated from full well stitched images (acquired as described above) by applying the Directionality function from ImageJ Fiji⁶⁹ to a centered 8 mm by 12 mm cropped region of the filtered stitched full well images. This region of interest captured the majority of the well, with the exception of the bubble trap and kinematic features at the edges of the well. Bin sizes of 2.022 degrees were used and the percent of fibers within ±20° of the mean direction for each replicate was computed by summing the normalized values of the polar fast Fourier transform power-spectral density provided by the ImageJ directionality plug-in.⁶⁹ The distributions shown in Fig. 2e and f were plotted using an adjusted version of the superviolin code package described in Lord et al. 2020.⁷⁹

Immunofluorescence images acquired at 40× magnification from the center of each well were used to quantify the fiber width and the number of nuclei per fiber. Segmentation for both murine and human fibers was first generated using ilastik, an open-source classifier for image-analysis and identification.⁸⁰ Specifically, the pixel-classification segmentation workflow was utilized to train the classifier on a series of representative 40× murine and human fiber samples. Then, segmentation for all fibers were outputted. Since the fibers are very close together, ilastik segmentation was manually checked by overlaying ilastik segmentation over the original fiber files in photoshop and then cleaned-up if necessary to ensure individual fibers would be recognized as separate objects in the next step of the data analysis path. The nuclei fluorescent channels stained with NucBlue for both cell types were segmented by using the cellpose nuclei identification package.⁸¹ A nucleus was considered inside a muscle fiber if at least 50% of its segmented area overlapped with that of a given muscle fiber's area (see Fig. 4a). At 40× magnification, individual fibers did not fully fit in the field of view. Therefore, we normalized the fusion index of a given fiber by its length to avoid biases coming from cropped fibers. As a result, we report fusion index as ‘nuclei per micron’. The fiber width for each fiber segment within the field of view was calculated by skeletonizing each fiber and calculating the shortest distance to the edge of the segmented fiber from each skeleton point making use of the MATLAB functions bwskel() and bwdist().⁸² The final reported width for each segmented fiber was then calculated by multiplying all the measured distances to the skeleton points by 2 and then taking the average value for each fiber. The average nuclei circularity of each biological replicate was reported using the MATLAB function regionprops() to calculate a circularity value between 0–1 for each segmented nuclei in each replicate.⁸² The average circularity for each replicate is reported in Fig. 4c.

Statistical analysis

Unless specified otherwise, all statistical tests were run in Python using functions from scipy.stats. The Y/X displacement ratios were compared to the theoretical mean of 1 (i.e. equal displacement in X and Y) using a Wilcoxon signed-rank test. For all tests comparing data obtained with all 5 different experimental conditions (12.5 μm, 25 μm, 125 μm, flat, unstamped), the following protocol was followed: every distribution was tested using the Shapiro–Wilk normality test (normal: p > 0.05). If all distributions to be compared were normal, they underwent an ANOVA followed by a Tukey's HSD post hoc test (using the function ‘post hoc_Tukey’ from the package scikit-post hocs⁸³) if the result of the ANOVA was significant. Similarly, non-normal distributions underwent a Kruskal–Wallis followed, in case of statistical significance, by Dunn's post hoc test with Bonferroni correction (using the package scikit-post hocs). Results were displayed on the graphs with the statannotation Python package.⁸⁴

Computational modeling

To model the contraction of the grooved fibrin/iris muscle, a thermal load simulation was created to mimic the strain applied by the muscle during contraction. First, the entire bilayer was created using Abaqus finite element analysis software. From there, the part was partitioned twice: once to separate the muscle layer from the fibrin (creating a 50um micron thickness for the muscle layer and a 1 mm thickness for the fibrin) and twice to partition the radial grooved section from the circumferential section. In the property module, three elastic materials were created all with ∼0.5 Poisson's ratio. The fibrin was entered as an elastic material with Young's module of 0.3 kPa and the two muscle materials were entered with a Young's modulus of 130 kPa, based on our previously published estimates of fibrin and muscle mechanical properties.^68,85 Two muscle materials were created to assign different thermal expansion directions to mimic the directionality of the stamped grooves. The circumferential muscle material was assigned a 0.067 thermal expansion value parallel to the force-generating axes of the fibers, and the same value was assigned to the radial muscle material in their corresponding fiber direction. The coordinate system was changed to cylindrical for the creation of these orthotropic materials. The 0.067 alpha value corresponds to 6.7% strain for a 1 °C temperature drop. This strain value was determined experimentally from video analysis by taking the normal and shear strains over the iris during contraction at 1 Hz, 10 V, 20% duty cycle, and calculating the maximum principal strain. An axisymmetric constraint about the z axis, as well as a zero-displacement constraint in the z axis for the bottom surface of the fibrin layer, were used for both the tethered and untethered models. For the tethered model, x and y displacement constraints (ranging from 10% to 90% gel height) were added to the sides of the gel to mimic adhesion to the wall of the well plate. 1900 hybrid linear 3D elements were used to mesh the entire iris, and a 1 °C temperature drop was imposed to invoke a contractile strain response in the muscle layer.

Author contributions

Conceptualization: T. R., L. S., R. R.; data curation: T. R., L. S., S. K.; formal analysis: T. R., L. S., S. K., M. B.; funding acquisition: R. R.; investigation: T. R., L. S., P. U.; methodology: T. R., L. S., S. K., M. B., R. H., O. T., A. L., R. R.; project administration: R. R.; resources: R. R.; software: T. R., L. S., S. K., M. B.; supervision: R. R.; validation: T. R., L. S., R. R.; visualization: T. R., L. S., M. B., R. R.; writing – original draft: T. R., L. S., M. B., R. R.; writing – reviewing and editing: T. R., L. S., R. R.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Anja Nordstrom from the Harvard Medical School Electron Microscopy facility for assistance with imaging. This work was supported in part by the US DoD Army Research Office Early Career Program and PECASE award (awarded to R. R.), NSF CAREER award (awarded to R. R.), US DoD Office of Naval Research Young Investigator Program (awarded to R. R.), the US DoD DURIP program (awarded to R. R.), the La Caixa Postdoctoral Fellowship at MIT (awarded to T. R.), the NIH T32 Neurobiological Engineering Training Program (awarded to L. S.), the NSF Graduate Research Fellowship Program (awarded to M. B. and S. K.), and the MIT MISTI Global Seed Funds Program. This work was carried out in part in the MIT.Nano facility.

References

1. C. McCuller, R. Jessu and A. L. Callahan, in StatPearls, StatPearls Publishing, Treasure Island (FL), 2023.
2. W. R. Frontera and J. Ochala, Behav. Genet., 2015, 45, 183–195.
3. T. Osaki, S. G. M. Uzel and R. D. Kamm, Nat. Protoc., 2020, 15, 421–449.
4. J. Gilbert-Honick and W. Grayson, Adv. Healthcare Mater., 2020, 9, 1–27.
5. A. Cheesbrough, P. Harley, F. Riccio, L. Wu, W. Song and I. Lieberam, Biofabrication, 2023, 15, 045020.
6. J. Wang, C. J. Zhou, A. Khodabukus, S. Tran, S. O. Han, A. L. Carlson, L. Madden, P. S. Kishnani, D. D. Koeberl and N. Bursac, Commun. Biol., 2021, 4, 1–14.
7. A. Urzi, I. Lahmann, L. V. N. Nguyen, B. R. Rost, A. García-Pérez, N. Lelievre, M. E. Merritt-Garza, H. C. Phan, G. J. Bassell, W. Rossoll, S. Diecke, S. Kunz, D. Schmitz and M. Gouti, Nat. Commun., 2023, 14, 8043.
8. R. Raman, L. Grant, Y. Seo, C. Cvetkovic, M. Gapinske, A. Palasz, H. Dabbous, H. Kong, P. P. Pinera and R. Bashir, Adv. Healthcare Mater., 2017, 1700030, 1700030.
9. E. Rousseau, R. Raman, T. Tamir, A. Bu, S. Srinivasan, N. Lynch, R. Langer, F. M. White and M. J. Cima, Biomaterials, 2023, 302, 122317.
10. L. Ricotti, B. Trimmer, A. W. Feinberg, R. Raman, K. K. Parker, R. Bashir, M. Sitti, S. Martel, P. Dario and A. Menciassi, Sci. Rob., 2017, 1–18.
11. R. Raman, Annu. Rev. Biomed. Eng., 2024, 26, 223–245.
12. V. A. Webster-Wood, M. Guix, N. W. Xu, B. Behkam, H. Sato, D. Sarkar, S. Sanchez, M. Shimizu and K. K. Parker, Bioinspiration Biomimetics, 2023, 18, 015001.
13. M. Bawa and R. Raman, Sci. Rob., 2024, 9, eadr9299.
14. J. Rivnay, R. Raman, J. T. Robinson, C. Schreib, T. Cohen-Karni, K. E. Galloway and O. Veiseh, Nat. Rev. Bioeng., 2025 DOI:10.1038/s44222-024-00262-6.
15. S. Ostrovidov, V. Hosseini, S. Ahadian, T. Fujie, S. P. Parthiban, M. Ramalingam, H. Bae, H. Kaji and A. Khademhosseini, Tissue Eng., Part B, 2014, 1–34.
16. F. Iberite, E. Gruppioni and L. Ricotti, npj Regenerative Medicine, 2022, 7(1), 23.
17. W. Bian and N. Bursac, Biomaterials, 2009, 30, 1401–1412.
18. R. Raman, C. Cvetkovic and R. Bashir, Nat. Protoc., 2017, 12, 519–533.
19. W. R. Legant, A. Pathak, M. T. Yang, V. S. Deshpande, R. M. McMeeking and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10097–10102.
20. A. Iuliano, M. Haalstra, R. Raghuraman, K. Bielawski, A. P. Bholasing, E. Van Der Wal, J. C. De Greef and W. W. M. P. Pijnappel, Adv. Mater. Technol., 2023, 2300845.
21. R. Raman, C. Cvetkovic, S. G. M. Uzel, R. J. Platt, P. Sengupta, R. D. Kamm and R. Bashir, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3497–3502.
22. Y. Morimoto, H. Onoe and S. Takeuchi, Sci. Rob., 2018, 3, eaat4440.
23. M. Guix, R. Mestre, T. Patiño, M. De Corato, J. Fuentes, G. Zarpellon and S. Sánchez, Sci. Rob., 2021, 6, eabe7577.
24. S. Davoudi, B. Xu, E. Jacques, J. L. Cadavid, M. McFee, C.-Y. Chin, A. Meysami, M. Ebrahimi, M. A. Bakooshli, K. Tung, H. Ahn, H. J. Ginsberg, A. P. McGuigan and P. M. Gilbert, Adv. Funct. Mater., 2021, 2106548, 1–15.
25. A. Cheesbrough, F. Sciscione, F. Riccio, P. Harley, L. R'Bibo, G. Ziakas, A. Darbyshire, I. Lieberam and W. Song, Adv. Mater., 2022, 34, 2110441.
26. B. Rios, A. Bu, T. Sheehan, H. Kobeissi, S. Kohli, K. Shah, E. Lejeune and R. Raman, Device, 2023, 1(4) DOI:10.1016/j.device.2023.100097.
27. K. Y. Lee, S.-J. Park, D. G. Matthews, S. L. Kim, C. A. Marquez, J. F. Zimmerman, H. A. M. Ardona, A. G. Klever, G. V. Lauder and K. K. Parker, Science, 2022, 375, 639–647.
28. S.-J. Park, M. Gazzola, K. S. Park, S. Park, V. Di Santo, E. L. Blevins, J. U. Lind, P. H. Campbell, S. Dauth, A. K. Capulli, F. S. Pasqualini, S. Ahn, A. Cho, H. Yuan, B. M. Maoz, R. Vijaykumar, J.-W. Choi, K. Deisseroth, G. V. Lauder, L. Mahadevan and K. K. Parker, Science, 2016, 353, 158–162.
29. S. R. Shin, S. M. Jung, M. Zalabany, K. Kim, P. Zorlutuna, S. B. Kim, M. Nikkhah, M. Khabiry, M. Azize, J. Kong, K. T. Wan, T. Palacios, M. R. Dokmeci, H. Bae, X. Tang and A. Khademhosseini, ACS Nano, 2013, 7, 2369–2380.
30. A. W. Feinberg, A. Feigel, S. S. Shevkoplyas, S. Sheehy, G. M. Whitesides and K. K. Parker, Science, 2007, 317, 1366–1370.
31. R. Xie, Y. Cao, R. Sun, R. Wang, A. Morgan, J. Kim, S. J. P. Callens, K. Xie, J. Zou, J. Lin, K. Zhou, X. Lu and M. M. Stevens, Sci. Adv., 2024, 10, eadl1549.
32. R. M. Duffy, Y. Sun and A. W. Feinberg, Ann. Biomed. Eng., 2016, 44, 2076–2089.
33. H. Jangir and J. J. Hickman, ACS Biomater. Sci. Eng., 2023, 9, 4698–4708.
34. P. Bajaj, B. Reddy, L. Millet, C. Wei, P. Zorlutuna, G. Bao and R. Bashir, Integr. Biol., 2011, 3, 897–909.
35. J. Chen, X. Chen, Y. Ma, Y. Liu, J. Li, K. Peng, Y. Dai and X. Chen, ACS Omega, 2023, 8, 41374–41382.
36. E. Ko, S. J. Yu, G. J. Pagan-Diaz, Z. Mahmassani, M. D. Boppart, S. G. Im, R. Bashir and H. Kong, Adv. Sci., 2019, 6, 1801521.
37. H. Mita, Y. Mizuno, H. Tanaka and T. Fujie, Biofabrication, 2024, 16, 025010.
38. S. R. Shin, S. M. Jung, M. Zalabany, K. Kim, P. Zorlutuna, S. bok Kim, M. Nikkhah, M. Khabiry, M. Azize, J. Kong and K. T. Wan, ACS Nano, 2013, 7(3), 2369–2380.
39. O. Chaudhuri, Biomater. Sci., 2017, 5, 1480–1490.
40. A. Bu, F. Afghah, N. Castro, M. Bawa, S. Kohli, K. Shah, B. Rios, V. Butty and R. Raman, Adv. Healthcare Mater., 2024, 2403712.
41. H. Takahashi, F. Oikawa, N. Takeda and T. Shimizu, Tissue Eng., Part A, 2022, 28, 661–671.
42. A. Balciunaite, O. Yasa, M. Filippi, M. Y. Michelis and R. K. Katzschmann, in 2024 IEEE 7th International Conference on Soft Robotics (RoboSoft), 2024, pp. 525–530.
43. O. Aydin, X. Zhang, S. Nuethong, G. J. Pagan-Diaz, R. Bashir, M. Gazzola and M. T. A. Saif, Proc. Natl. Acad. Sci. U. S. A., 2019, 201907051.
44. C. M. Nelson, J. L. Inman and M. J. Bissell, Nat. Protoc., 2008, 3, 674–678.
45. S. Hinds, W. Bian, R. G. Dennis and N. Bursac, Biomaterials, 2011, 32, 3575–3583.
46. R. Raman, C. Cvetkovic and R. Bashir, Nat. Protoc., 2017, 12, 519–533.
47. R. Mestre, N. García, T. Patiño, M. Guix, J. Fuentes, M. Valerio-Santiago, N. Almiñana and S. Sánchez, Biofabrication, 2021, 13, 045011.
48. C. Cvetkovic, R. Raman, V. Chan, B. J. Williams, M. Tolish, P. Bajaj, M. S. Sakar, H. H. Asada, M. T. A. Saif and R. Bashir, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10125–10130.
49. S. L. Das, B. P. Sutherland, E. Lejeune, J. Eyckmans and C. S. Chen, Am. J. Physiol.: Heart Circ. Physiol., 2022, 323, H738–H748.
50. HibaKob, Raman_Manuscript_2023https://github.com/HibaKob/Raman_Manuscript_2023 2023.
51. J. Bloom, M. Motlagh and C. Czyz, in StatPearls.
52. G. J. Pagan-Diaz, X. Zhang, L. Grant, Y. Kim, O. Aydin, C. Cvetkovic, E. Ko, E. Solomon, J. Hollis and H. Kong, Adv. Funct. Mater., 2018, 1801145, 1–13.
53. V. Hosseini, S. Ahadian, S. Ostrovidov, G. Camci-Unal, S. Chen, H. Kaji, M. Ramalingam and A. Khademhosseini, Engineered Contractile Skeletal Muscle Tissue on a Microgrooved Methacrylated Gelatin Substrate, https://www.liebertpub.com/doi/10.1089/ten.tea.2012.0181, (accessed April 17, 2024).
54. K.-Y. Huang, G. Upadhyay, Y. Ahn, M. Sakakura, G. J. Pagan-Diaz, Y. Cho, A. C. Weiss, C. Huang, J. W. Mitchell, J. Li, Y. Tan, Y.-H. Deng, A. Ellis-Mohr, Z. Dou, X. Zhang, S. Kang, Q. Chen, J. V. Sweedler, S. G. Im, R. Bashir, H. J. Chung, G. Popescu, M. U. Gillette, M. Gazzola and H. Kong, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2313590121.
55. L. Altomare, N. Gadegaard, L. Visai, M. C. Tanzi and S. Farè, Acta Biomater., 2010, 6, 1948–1957.
56. S. Wu, L. Ruan, J. Wu, M. Wu, L. T. Chu, H. K. Kwong, M. L. Lam and T.-H. Chen, Biofabrication, 2023, 15, 025015.
57. J. C. Nawroth, H. Lee, A. W. Feinberg, C. M. Ripplinger, M. L. McCain, A. Grosberg, J. O. Dabiri and K. K. Parker, Nat. Biotechnol., 2012, 30, 792–797.
58. L. Ricotti, S. Taccola, V. Pensabene, V. Mattoli, T. Fujie, S. Takeoka, A. Menciassi and P. Dario, Biomed. Microdevices, 2010, 12, 809–819.
59. T. H. Kim, C. H. Kwon, C. Lee, J. An, T. T. T. Phuong, S. H. Park, M. D. Lima, R. H. Baughman, T. M. Kang and S. J. Kim, Sci. Rep., 2016, 6, 26687.
60. K. Shimizu, H. Kassai, Y. Kamei, K. Yamamoto, T. Nagashima, T. Maekawa, H. Akiyama and H. Honda, Cells, 2022, 11, 3760.
61. M. L. McCain, A. Agarwal, H. W. Nesmith, A. P. Nesmith and K. K. Parker, Biomaterials, 2014, 35, 5462–5471.
62. E. Kim, S. Jeon, H.-K. An, M. Kianpour, S.-W. Yu, J. Kim, J.-C. Rah and H. Choi, Sci. Adv., 2020, 6, eabb5696.
63. N. Xia, R. Liu, W. Chen, D. Wang and L. Sun, Eng. Regener., 2023, 4, 451–461.
64. C. H. Park, K.-H. Kim, Y.-M. Lee, W. V. Giannobile and Y.-J. Seol, Int. J. Mol. Sci., 2017, 18, 1927.
65. L. S. Prahl, C. M. Porter, J. Liu, J. M. Viola and A. J. Hughes, iScience, 2023, 26, 106657.
66. B. Ergaz, S. Goren and A. Lesman, Biofabrication, 2023, 16, 015012.
67. Application Guide, https://dental.formlabs.com/eu/indications/surgical-guides/guide/, (accessed July 30, 2024).
68. A. Bu, F. Afghah, N. Castro, M. Bawa, S. Kohli, K. Shah, B. Rios, V. Butty and R. Raman, bioRxiv, 2024, preprint,  DOI:10.1101/2024.03.02.583091.
69. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
70. D. Hülagü, C. Tobias, E. Climent, A. Gojani, K. Rurack and V.-D. Hodoroaba, Adv. Eng. Mater., 2022, 24, 2101344.
71. Z. Al Tanoury, J. F. Zimmerman, J. Rao, D. Sieiro, H. M. McNamara, T. Cherrier, A. Rodríguez-delaRosa, A. Hick-Colin, F. Bousson, C. Fugier-Schmucker, F. Marchiano, B. Habermann, J. Chal, A. P. Nesmith, S. Gapon, E. Wagner, V. A. Gupta, R. Bassel-Duby, E. N. Olson, A. E. Cohen, K. K. Parker and O. Pourquié, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2022960118.
72. T. Kluyver, B. Ragan-Kelley, F. Pérez, B. Granger, M. Bussonnier, J. Frederic, K. Kelley, J. Hamrick, J. Grout, S. Corlay, P. Ivanov, D. Avila, S. Abdalla, C. Willing and Jupyter development team, Jupyter Notebooks–a publishing format for reproducible computational workflows. In Positioning and power in academic publishing: Players, agents and agendas, IOS Press, 2016, pp. 87–90.
73. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
74. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272.
75. T. pandas development team, pandas-dev/pandas (version v1.5.3) Zenodo 2023.
76. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
77. M. L. Waskom, J. Open Source Softw., 2021, 6, 3021.
78. G. Bradski, Dr Dobb's Journal: Software Tools for the Professional Programmer.
79. S. J. Lord, K. B. Velle, R. D. Mullins and L. K. Fritz-Laylin, J. Cell Biol., 2020, 219, e202001064.
80. S. Berg, D. Kutra, T. Kroeger, C. N. Straehle, B. X. Kausler, C. Haubold, M. Schiegg, J. Ales, T. Beier, M. Rudy, K. Eren, J. I. Cervantes, B. Xu, F. Beuttenmueller, A. Wolny, C. Zhang, U. Koethe, F. A. Hamprecht and A. Kreshuk, Nat. Methods, 2019, 16, 1226–1232.
81. C. Stringer, T. Wang, M. Michaelos and M. Pachitariu, Nat. Methods, 2021, 18, 100–106.
82. Signal Processing and Machine Learning Techniques for Sensor Data Analytics.
83. M. A. Terpilowski, J. Open Source Software, 2019, 4, 1169.
84. M. Weber, statannot (version 0.2.3) https://github.com/webermarcolivier/statannot.
85. N. Lynch, N. Castro, T. Sheehan, L. Rosado, B. Rios, M. Culpepper and R. Raman, Adv. Intell. Syst, 2024, 6(7), 2300834.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4bm01017e

‡ These authors contributed equally to the manuscript.

---