Electrically and magnetically readable memory with a graphene/1T-CrTe2 heterostructure: anomalous Hall transistor†
Surabhi
Menon
 and
Umesh V.
Waghmare
and
Umesh V.
Waghmare
 *
*
Jawaharlal Nehru Centre for Advanced Scientific Research, Theoretical Sciences Unit, Bangalore 560064, India. E-mail: waghmare@jncasr.ac.in
First published on 26th November 2024
Abstract
Using first-principles theoretical analysis, we demonstrate the spin-polarized anomalous Hall conductivity (AHC) response of a 2D vdW heterostructure of graphene and ferromagnetic CrTe2 that can be controlled with a perpendicular electric field E. The origins of AHC and linear magnetoelectric responses are traced to (a) the transfer of electronic charge from graphene to ferromagnetic CrTe2 causing an out-of-plane electric polarization P = 1.69 μC cm−2 and (b) the crystal field and spin-split Dirac points of graphene. Through H′ = −VP·E coupling, E controls the charge transfer, magnetization and carrier density, switching the spin-polarized Berry curvature as the Fermi energy crosses the split Dirac points of graphene. Based on these, we propose an Anomalous Hall Transistor (AHT) that exploits electronic spin and charge to store binary information, opening up a route to quantum devices based on quantum geometry and magnetoelectric transport.
1 Introduction
Van der Waals (vdW) heterostructures formed by stacking of two-dimensional materials are emerging as systems with remarkable diversity in properties, opening up opportunities to explore fascinating physics1 and to develop devices.2 In 2D heterostructures, strong covalent bonds provide sufficient in-plane stability and relatively weak vdW interactions keep the stack together. In a heterostructure of monolayers of two distinct 2D materials, the interface itself becomes an interesting system with symmetry and properties that may not be exhibited by the individual monolayers. vdW heterostructures of graphene and other 2D materials serve as a rich platform to explore various properties.3Two-dimensional ferromagnetism was reported in Cr2Ge2Te6,4 CrI3,5 and MnSe2.6 By integrating a nonmagnetic material with a magnetic material in a heterostructure, the time-reversal symmetry is broken and its electronic structure is altered due to interaction with the magnetic layer.7 Recent work shows magnetic proximity effects driven by spin-dependent hybridization between graphene and CrI3.8 A strong exchange field across the interface and the associated magnetic proximity effect have been demonstrated to tune the spin and valley-polarization of various heterostructures such as graphene on CrBr3,9 graphene on CrI3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and CrI3 on WTe2.11
10 and CrI3 on WTe2.11
CrTe2 is a TMD that crystallizes in a centrosymmetric 1T structure, in which the chromium hexagonal planes are sandwiched by tellurium hexagonal planes with ABC stacking. Bulk 1T-CrTe2 has a layered structure with a ferromagnetic critical temperature of ∼320 K, which decreases slightly to near room temperature in its monolayered form.12–14 A combination of magnetization and spin–orbit coupling (SOC) helps in producing spin-polarized charge carriers, which contribute to the anomalous Hall effect. This was first explained by Karplus and Luttinger in 1954![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 as arising from spin-dependent scattering processes of charge carriers in ferromagnetic materials.16 While a large anomalous Hall effect was observed in bulk 1T-CrTe2, it reduces with its thickness to significantly low values of AHC in monolayered 1T-CrTe2.17,18
15 as arising from spin-dependent scattering processes of charge carriers in ferromagnetic materials.16 While a large anomalous Hall effect was observed in bulk 1T-CrTe2, it reduces with its thickness to significantly low values of AHC in monolayered 1T-CrTe2.17,18
In this work, we demonstrate the emergence of linear magnetoelectric coupling and a spin-dependent anomalous Hall effect in the van der Waals heterostructure of graphene and monolayered 1T-CrTe2. Based on their control with a gating E-field, we propose an Anomalous Hall Transistor (AHT). The AHC is a result of spin-dependent Berry curvature of the graphene layer arising at its Dirac points that are split by the crystal field and spin-dependent interaction with CrTe2. In contrast to either the CrTe2 monolayer or graphene, their heterostructure exhibits a sizeable linear magnetoelectric effect due to broken inversion and time-reversal symmetries. In contrast to the spin Hall transistor,19 which is based on the transport controlled by spin–orbit coupling (SOC), the AHT proposed here relies on spin and crystal field split bands at the Dirac point of graphene and not the SOC whose splitting is weak.
2 Computational methods
Our first-principles calculations are based on density functional theory (DFT) within the Generalized Gradient Approximation (GGA)20 of the exchange–correlation energy with a functional parameterized by Perdew–Burke–Ernzerhof (PBE) as implemented in the QUANTUM ESPRESSO package,21 which employs a plane-wave basis. Interactions between ionic cores and valence electrons are represented using Projector Augmented Wave (PAW) scalar relativistic potentials.22,23 We use fully relativistic PAW potentials in calculations to capture the effects of spin–orbit coupling (SOC). We use an energy cutoff of 60 Ry to truncate the plane-wave basis used to represent wave functions and a charge density cutoff of 500 Ry. VdW interactions are taken into account between graphene and the ferromagnetic monolayer 1T-CrTe2 using the DFT-D2 method proposed by Grimme.24 The occupation numbers of electronic states are smeared using the Fermi–Dirac distribution and a smearing width (kBT) of 0.003 Ry. The electronic correlation effects of Cr-3d orbitals are included using the DFT+U approach of Cococcioni25 with a Hubbard U parameter of 2 eV as used by S. Li et al.18 We used a periodic supercell made of 3 × 3 and 2 × 2 in-plane supercells of graphene and 1T-CrTe2, and sampled Brillouin zone (BZ) integrations on a uniform grid of 7 × 7 × 1 k-points. Berry curvature and anomalous Hall conductivity (AHC) were calculated using the WANNIER90 code.26 We simulated an external electric field applied perpendicular to the 2D heterostructure using a sawtooth periodic potential.213 Results and discussion
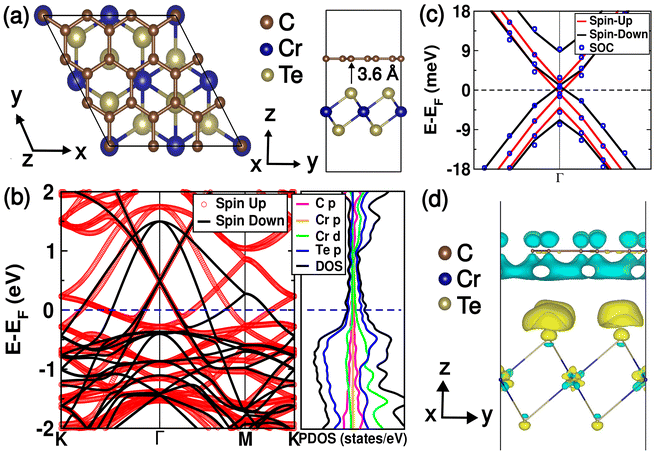
Our estimates of the lattice parameters of the monolayer forms of graphene and 1T-CrTe2 (centrosymmetric space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (No. 164)) are 2.46 Å and 3.71 Å, in good agreement with experiments.27,28 While monolayers of 1T-CrTe2 and graphene are centrosymmetric, their heterostructure is noncentrosymmetric. The heterostructure of graphene and monolayer 1T-CrTe2 (see Fig. 1(a)) in the relaxed ferromagnetic structure has a lattice constant of 7.415 Å, in which the graphene lattice is expanded by 0.5%, whereas the CrTe2 layer is contracted by 0.1%. The interlayer distance between graphene and monolayer CrTe2 (graphene/1T-CrTe2) is 3.6 Å with a vacuum of 8 Å along the z-direction. The exchange coupling J > 0 (see Table 1 of the ESI†) for both systems supporting the FM ground state. Since J of the heterostructure is 20% greater than that of monolayer 1T-CrTe2, the Curie temperature of the heterostructure is expected (noting that the interlayer coupling is weak) to be higher than that of monolayer 1T-CrTe2.
m1 (No. 164)) are 2.46 Å and 3.71 Å, in good agreement with experiments.27,28 While monolayers of 1T-CrTe2 and graphene are centrosymmetric, their heterostructure is noncentrosymmetric. The heterostructure of graphene and monolayer 1T-CrTe2 (see Fig. 1(a)) in the relaxed ferromagnetic structure has a lattice constant of 7.415 Å, in which the graphene lattice is expanded by 0.5%, whereas the CrTe2 layer is contracted by 0.1%. The interlayer distance between graphene and monolayer CrTe2 (graphene/1T-CrTe2) is 3.6 Å with a vacuum of 8 Å along the z-direction. The exchange coupling J > 0 (see Table 1 of the ESI†) for both systems supporting the FM ground state. Since J of the heterostructure is 20% greater than that of monolayer 1T-CrTe2, the Curie temperature of the heterostructure is expected (noting that the interlayer coupling is weak) to be higher than that of monolayer 1T-CrTe2.
We begin with analysis of the electronic structure and partial density of states (PDOS) of the heterostructure (see Fig. 1(b)). The graphene/1T-CrTe2 vdW heterostructure is metallic and the states at its Fermi level involve both C-based sp2 states and hybridization of Te-5p and Cr-3d orbitals. Γ, K and K′ points in the BZ of graphene fold to the Γ point of its 3 × 3 supercell. Since we treat spin-polarization explicitly in our calculations, there are eight bands linearly dispersed at the Γ point (see Fig. 1(c)), which include four (two bands each at K and K′ valleys) bands each for the spin-up and spin-down channels. The interaction of the 2D magnetic layer of CrTe2 with graphene involves electronic charge transfer leading to energy shift and subtle splittings in the Dirac points due to the chemical crystal field and magnetic exchange. While the bands of monolayered 1T-CrTe2 are not affected significantly, the electronic bands at the Dirac point of graphene shift to 0.49 eV above the Fermi level, and the spin-up and spin-down electronic bands at the Γ point split further opening an energy gap of 2.5 meV due to interfacial exchange interaction. In the ground state, the magnetic ordering of the heterostructure is ferromagnetic with a magnetization of 10.69μB per u.c, quite close to our estimate of magnetization of monolayered 1T-CrTe2 (of 10.64μB per u.c).
In the graphene/1T-CrTe2 heterostructure, inversion and time-reversal symmetries are broken due to the interfacial structure and ferromagnetic order of 1T-CrTe2, respectively. Of the four spin-up bands at the Dirac point (see Fig. 1(c)), two split away from the Dirac point by about ∼6 meV. Similarly, two of the four spin-down bands undergo a splitting of ∼16 meV. With the inclusion of SOC, energy splitting is ∼200 μeV estimated using the Vienna Ab initio Simulation Package (VASP).22,29 Thus, the effects of SOC on the bands at the Dirac points are an order of magnitude smaller than that of the crystal field and exchange interactions. Thus, the SOC does not influence the spin-dependent anomalous Hall conductivity of graphene. Splittings of bands of a particular spin arise from the crystal field, which scatters electrons between the K and K′ valleys of graphene. Energy shift in the Dirac points of graphene with respect to EF is understood from electron transfer from graphene to the 1T-CrTe2 layer. To analyze such electron transfer, we determined the electron density difference,
| Δρ = ρgraphene/1T-CrTe2 − ρGr − ρML-CrTe2 | (1) |
To understand the subtle changes and gap opening at the Dirac points of graphene, we present here a model Hamiltonian within the k·p approximation. The honeycomb lattice of graphene has a basis of two atoms in the primitive unit cell (see ESI, Fig. S12†), and its hexagonal BZ has two symmetry inequivalent corners, 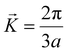
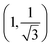 and
and 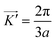
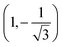 , where a is the carbon–carbon distance. The low energy electronic structure at the Dirac points is represented by a Hamiltonian expanded in
, where a is the carbon–carbon distance. The low energy electronic structure at the Dirac points is represented by a Hamiltonian expanded in 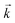 at the K′ point:30
at the K′ point:30
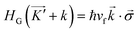 | (2) |
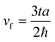 , t is the nearest neighbor hopping interaction parameter and
, t is the nearest neighbor hopping interaction parameter and 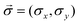 are Pauli matrices. Energy eigenvalues are given by
are Pauli matrices. Energy eigenvalues are given by 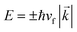 . Similarly, H for states near the K point is
. Similarly, H for states near the K point is 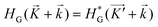 .30,31 As the K and K′ points fold onto the Γ point, we construct a four band Hamiltonian H, including the perturbations due to the staggered AB sublattice potential and effective crystal field of CrTe2. It acts on the basis of pz orbitals at A and B sublattices,
.30,31 As the K and K′ points fold onto the Γ point, we construct a four band Hamiltonian H, including the perturbations due to the staggered AB sublattice potential and effective crystal field of CrTe2. It acts on the basis of pz orbitals at A and B sublattices, 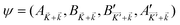 :
:| H = H0 + ΔHc | (3) |
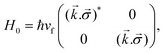 | (4) |
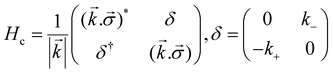 | (5) |
We next present results for the effects of carrier doping on the electronic and magnetic properties of the heterostructure. We dope the graphene/1T-CrTe2 heterostructure with half an electron per unit cell of the heterostructure. The gap opened at the Dirac points of the heterostructure further widens as shown in a schematic in Fig. 2(a). We note that the Dirac points of graphene shift down by 0.49 eV and are pinned at the Fermi level with electron doping. The spin-polarized electronic structure of the doped heterostructure (see Fig. 2(b)) exhibits enhanced splittings of ε1 = 8.5 meV and ε2 = −9.9 meV due to the n-type carrier doping associated with further electron transfer from graphene to the 1T-CrTe2 layer (see ESI, Fig. S5†). We find an increase in polarization from 1.69 μC cm−2 to 3.0 μC cm−2 upon electron doping. Next, we determine the response of the heterostructure to a perpendicular electric field, in exploration of a linear magnetoelectric (ME) effect allowed by symmetry.32 The ME effect results in the induction of magnetization with the applied electric field or the induction of electric polarization with the applied magnetic field.33 Magnetization along with polarization in these ME materials allows multiple control fields for developing new devices. ME coupling between E and H fields can be described by the thermodynamic free energy per volume (F) of a material:34
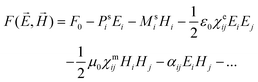 | (6) |
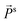 and
and 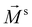 are the spontaneous polarization and magnetization, respectively, and χe, χm and α are the electric and magnetic susceptibilities and linear ME coupling, respectively. The interaction H′ = −VP·E governs the electric field induced change in dipole P through charge transfer, which shifts the bands. Thus, H′ = −VP·E coupling essentially alters the band filling necessary to access the physics of states at the Dirac points of graphene. Electric polarization can be obtained by differentiating the above equation by the electric field E,
are the spontaneous polarization and magnetization, respectively, and χe, χm and α are the electric and magnetic susceptibilities and linear ME coupling, respectively. The interaction H′ = −VP·E governs the electric field induced change in dipole P through charge transfer, which shifts the bands. Thus, H′ = −VP·E coupling essentially alters the band filling necessary to access the physics of states at the Dirac points of graphene. Electric polarization can be obtained by differentiating the above equation by the electric field E,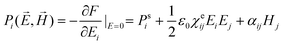 | (7) |
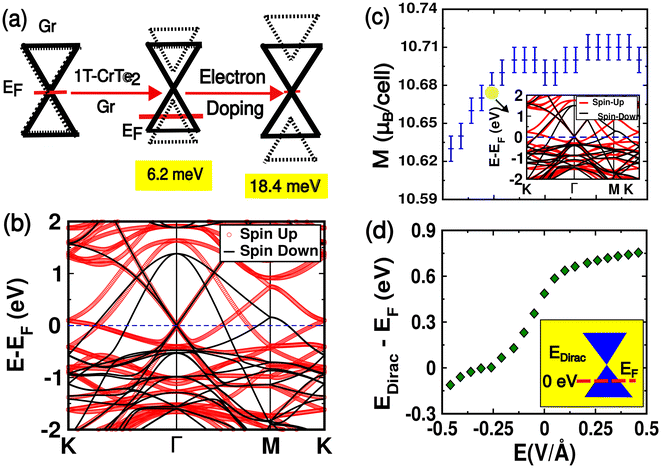 | ||
| Fig. 2 Responses of the graphene/1T-CrTe2 heterostructure to electron doping and an electric field. (a) A schematic of the electronic structure (spin-up) showing how a gap opens up at the Dirac points of the heterostructure, which increases with electron doping. The spin-resolved electronic structure and projected density of states (PDOS) of graphene/1T-CrTe2 doped with half an electron per unit cell (b) show that Dirac points are pinned at the Fermi level (EF). In response to the electric field perpendicular to the heterostructure, magnetization changes asymmetrically with ±0.01μB per u.c error bars (c) and its origin is traced to the asymmetry in the DOS at EF (Fig. 1(b)) and field induced shift in the Dirac points of graphene relative to EF shown in (d). Inset in (c) shows the spin-resolved electronic structure of the graphene/1T-CrTe2 heterostructure subjected to E = −0.26 V Å−1, similar to that of the doped heterostructure shown in (b). | ||
Similarly, magnetization is
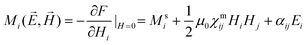 | (8) |
The linear ME coupling αij can be nonzero when the time reversal and inversion symmetries are broken, leading to a magnetization response to the electric field or a polarization response to the magnetic field. We use
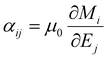 | (9) |
to estimate α of the graphene/1T-CrTe2 heterostructure involving interplay between the electronic spin and charge degrees of freedom across the interface. Our simulations (Ez < 0) show that M varies linearly with E (see Fig. 2(c)), and the estimate of magnetoelectric coupling α using an effective thickness of 7 Å of the heterostructure is ∼0.80 ps m−1, which is weaker than the experimental magnetoelectric coefficients of other materials such as Cr2O3 (4.13 ps m−1 at 298 K)35 and LiCoPO4 (30.6 ps m−1 at 4.2 K).36
A perpendicular electric field couples directly with Pz and can be used to tune the charge transfer and hence the Fermi energy relative to the Dirac points of graphene and access its frontier states. The energy of the Dirac point relative to the Fermi level shifts asymmetrically with positive and negative electric fields Ez.‡ The Fermi level shifts deeper into the valence band and towards the conduction band of graphene with positive and negative electric fields, respectively (see Fig. 2(d)). At Ez ∼−0.26 V Å−1 (see the spin-resolved electronic structure of graphene/1T-CrTe2 in Fig. 2(c)), the Dirac points of graphene are pinned at the Fermi level (see the inset of Fig. 2(c)). We find that CrTe2 bands remain unaffected under the application of positive and negative electric fields (see ESI, Fig. S14†). Shifts in the Dirac point with Ez can be understood in terms of the charge density difference. In the undoped heterostructure, electron transfer from graphene to the 1T-CrTe2 layer creates an intrinsic dipole moment and an electric field across the heterostructure. At positive Ez, additional electronic charge is transferred from graphene to the 1T-CrTe2 layer, strengthening its p-type behavior. Electron transfer from graphene to CrTe2 reduces with the negative electric field promoting n-type carriers at a slower rate, which are responsible for asymmetry in the M(E) response (Fig. 2(d)).
To analyze the electronic topological properties of the heterostructure, we obtained the Berry curvature and anomalous Hall conductivity (AHC) using maximally localized Wannier functions (MLWFs)37 constructed with projections of bands onto electronic states having the symmetry of C s, C p, Cr s, Cr p, Cr d, Te s and Te p orbitals. The Berry curvature (Ωzn)38,39 of the nth band at k of |ψnk〉 is
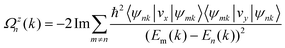 | (10) |
f n being the Fermi–Dirac distribution function, vi is the velocity operator along the i direction and En(k) is its energy eigenvalue. The Berry curvature of spin-up and spin-down states of a doped heterostructure (see ESI, Fig. S10†) is sizeable in the neighborhood of the Γ point and changes sign as the Fermi level moves across Dirac points. We find an interesting spin contrast: the Berry curvature (Fig. 3(a)) of spin-up is nonzero for μ < ED and that of spin-down is nonzero for μ > ED, arising from the combination of exchange and crystal field splittings. The intrinsic AHC is obtained from the Brillouin zone integral of the Berry curvature,40,41
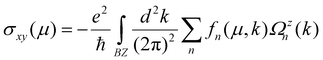 | (11) |
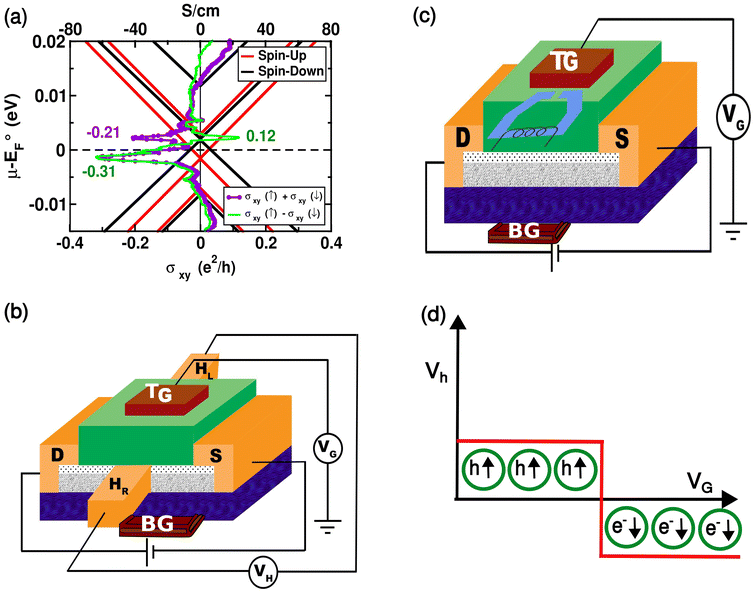
To assess its feasibility in terms of realistic devices, we simulated a field effect transistor setup42 as implemented in the Quantum Espresso package. The length of the periodic cell is L in the z-direction (Fig. S18(a)†). A 2D charged plate, representing a gate electrode (counter charge to neutralize the charge of doped carriers), was positioned at z = 0.0195 L. To prevent doped carriers from moving too close to the gate electrode, a dielectric potential barrier with a height of V = 1.5 Ry and a width of 0.175 L was employed. We also included a dipole correction with oppositely charged plates to eliminate the electrostatic interactions between periodic images. A dipole correction of −1.99 V Å−1 was applied in the positive z-direction to account for the electronic (heterostructure) and monopole charges. In the electronic structure of the gated heterostructure, the Dirac points of graphene shift to 0.05 eV above the Fermi level. The contributions by anomalous Hall charge conductivity (σxy (↑) + σxy (↓)) and anomalous Hall spin conductivity (σxy (↑) − σxy (↓)) were determined as a function of Fermi energy (EF), as shown in Fig. 3(a). The peak of −0.31 e2 h−1 below the Fermi level shows contributions from both charge and spin currents while charge and spin currents have opposite signs but comparable magnitudes when EF > 0. This supports the gating field switchable spin-polarized Hall signal (shown in Fig. 3(d)). Our estimates of the intrinsic AHC (σxy) of the half-electron doped gated heterostructure are ∼−78 S cm−1 and ∼−41 S cm−1 for spin-up and spin-down channels, respectively, which are weaker than of other materials such as FePt, NiPt and CoPt, exhibiting σxy of 1031 S cm−1, −826 S cm−1 and 481 S cm−1, respectively.43 However, the anomalous Hall conductivity of the graphene/1T-CrTe2 heterostructure is spin-polarized, because of the split Dirac points (see Fig. 1(c)).
We note that the effects of spin–orbit coupling (see ESI, Fig. S9†) will alter our results slightly but are expected to be weak as our focus is on electrons in graphene. Secondly, the AHC has other contributions (based on scattering) arising from the magnetism of CrTe2.15 However, these are large in thick films of CrTe2 and rather weak in the monolayered CrTe2.17,18 At the reference electric field of −0.26 V Å−1, we expect the charge transport to be dominated by graphene due to its high mobility and also the fact that its AHC arises from the quantum geometry of its electronic structure.
We now propose an Anomalous Hall Transistor (AHT) (see the schematic in Fig. 3(b) and (c)) as a storage device that allows the reading of binary information by sensing the spin and charge of Hall carriers, respectively. The device consists of an active channel made of the graphene/1T-CrTe2 heterostructure sandwiched between a dielectric and a substrate and is attached to source (S) and drain (D) electrodes. The voltage (VG) applied to top (TG) and bottom (BG) gate electrodes44 allows independent modulation of carrier doping (charge density) or the Fermi energy of the channel by VTG + VBG and VTG − VBG perpendicular electric fields, respectively. The latter can be used to achieve E = −0.26 V Å−1, at which the Dirac points pin to the Fermi level. In one configuration (Fig. 3(b)), the device incorporates a magnetic head that senses the spin of Hall carriers and converts it into an electrical signal functioning as a read-head. In another configuration, shown in Fig. 3(c), the device has transverse Hall electrodes (HR and HL) dedicated to measuring the Hall voltage (VH), thus reading information using the electric charge of Hall carriers.
The reference gate field (E = −0.26 V Å−1) is needed to achieve pinning of EF at the Dirac points, as discussed earlier (Fig. 2(b)). The device operation is based on the fact that the anomalous Hall conductivity (AHC) is nonzero primarily for the spin-up channel (σ↑xy > 0) when the gate voltage VG < 0 and for the spin-down channel (σ↓xy < 0) when VG > 0 (see Fig. 3(d)). The hallmark of this AHT storage device is its capability to read and store information using both spin and charge of Hall carriers. The AHT device proposed here should be operable at low temperatures, T < 100 K, because Δμ ∼8 meV. We note that the proposed AHT has the functionality of both spin and charge based binary information storage, as it is based on the electrically switchable spin-polarized anomalous Hall conductivity of the graphene/1T-CrTe2 heterostructure. On the other hand, the spin Hall transistor (SHT)19,45 relies on the spin Hall effect (SHE) originating from the relativistic spin–orbit coupling (SOC) that can be used to electrically generate or detect spin currents in non-magnetic systems (composed of heavy elements). AHT effectively unites the benefits of spin-based and charge-based paradigms, offering a simple yet rich platform for applications in semiconductor and quantum devices.
4 Conclusions
In summary, we presented theoretical analysis of a van der Waals heterostructure formed from graphene and monolayered 1T-CrTe2, showing that the Dirac points of graphene shift up in energy due to the transfer of electrons to 1T-CrTe2, and split due to exchange and crystal fields. It is shown to exhibit a sizeable linear magnetoelectric coupling of 0.80 ps m−1; coupled with intrinsic electric polarization Pz, its Fermi level can be tuned with a perpendicular electric field introducing p-type or n-type carriers and spin-dependent Berry curvature as the EF crosses the Dirac points, effectively introducing the spin-dependent AHC in graphene. Using a combination of the AHE and the high mobility of graphene, we propose an anomalous Hall transistor device, with the functionality of spin and charge based binary information storage based on the electrically switchable spin-polarized anomalous Hall conductivity of the heterostructure.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
U. V. W. and S. M. have filed an Indian Patent Application (pending) (202441059434) related to the anomalous Hall transistor device.Acknowledgements
S. M. acknowledges JNCASR for a fellowship and U. V. W. thanks DST-SERB, Govt. of India, for support through a J. C. Bose National Fellowship.References
- P. Ajayan, P. Kim and K. Banerjee, Phys. Today, 2016, 69, 38 CrossRef CAS.
- Y. Liu, N. O. Weiss, X. Duan, H.-C. Cheng, Y. Huang and X. Duan, Nat. Rev. Mater., 2016, 1, 1–17 Search PubMed.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang and Y. Wang, et al. , Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, et al. , Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- D. J. O'Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta and D. W. McComb, et al. , Nano Lett., 2018, 18, 3125–3131 CrossRef PubMed.
- M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419 CrossRef CAS PubMed.
- C. Cardoso, A. T. Costa, A. H. MacDonald and J. Fernández-Rossier, Phys. Rev. B, 2023, 108, 184423 CrossRef CAS.
- S. K. Behera, M. Bora, S. S. P. Chowdhury and P. Deb, Phys. Chem. Chem. Phys., 2019, 21, 25788–25796 RSC.
- M. U. Farooq and J. Hong, npj 2D Mater. Appl., 2019, 3, 1–7 CrossRef CAS.
- A. Bano, J. Krishna, T. Maitra and N. Gaur, Sci. Rep., 2019, 9, 1–8 CrossRef CAS PubMed.
- X. Sun, W. Li, X. Wang, Q. Sui, T. Zhang, Z. Wang, L. Liu, D. Li, S. Feng and S. Zhong, et al. , Nano Res., 2020, 13, 3358–3363 CrossRef CAS.
- X. Zhang, Q. Lu, W. Liu, W. Niu, J. Sun, J. Cook, M. Vaninger, P. F. Miceli, D. J. Singh and S.-W. Lian, et al. , Nat. Commun., 2021, 12, 1–9 CrossRef PubMed.
- L. Meng, Z. Zhou, M. Xu, S. Yang, K. Si, L. Liu, X. Wang, H. Jiang, B. Li and P. Qin, et al. , Nat. Commun., 2021, 12, 1–8 CrossRef PubMed.
- R. Karplus and J. Luttinger, Phys. Rev., 1954, 95, 1154 CrossRef.
- N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539 CrossRef.
- M. Huang, S. Wang, Z. Wang, P. Liu, J. Xiang, C. Feng, X. Wang, Z. Zhang, Z. Wen and H. Xu, et al. , ACS Nano, 2021, 15, 9759–9763 CrossRef CAS PubMed.
- S. Li, S.-S. Wang, B. Tai, W. Wu, B. Xiang, X.-L. Sheng and S. A. Yang, Phys. Rev. B, 2021, 103, 045114 CrossRef CAS.
- J. Wunderlich, B.-G. Park, A. C. Irvine, L. P. Zârbo, E. Rozkotová, P. Nemec, V. Novák, J. Sinova and T. Jungwirth, Science, 2010, 330, 1801–1804 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- G. Yang, L. Li, W. B. Lee and M. C. Ng, Sci. Technol. Adv. Mater., 2018, 19, 613–648 CrossRef CAS PubMed.
- K. Lasek, P. M. Coelho, K. Zberecki, Y. Xin, S. K. Kolekar, J. Li and M. Batzill, ACS Nano, 2020, 14, 8473–8484 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- C. Bena and G. Montambaux, New J. Phys., 2009, 11, 095003 CrossRef.
- A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef.
- I. E. Dzyaloshinskii, J. Exp. Theor. Phys., 1960, 10, 628–629 Search PubMed.
- G. Lawes and G. Srinivasan, J. Phys. D: Appl. Phys., 2011, 44, 243001 CrossRef.
- M. Fiebig, J. Phys. D: Appl. Phys., 2005, 38, R123 CrossRef CAS.
- G. Rado and V. Folen, Phys. Rev. Lett., 1961, 7, 310 CrossRef.
- J.-P. Rivera, Ferroelectrics, 1994, 161, 147–164 CrossRef CAS.
- N. Marzari and D. Vanderbilt, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 56, 12847 CrossRef CAS.
- D. J. Thouless, M. Kohmoto, M. P. Nightingale and M. den Nijs, Phys. Rev. Lett., 1982, 49, 405 CrossRef CAS.
- Y. Yao, L. Kleinman, A. MacDonald, J. Sinova, T. Jungwirth, D.-s. Wang, E. Wang and Q. Niu, Phys. Rev. Lett., 2004, 92, 037204 CrossRef PubMed.
- N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539 CrossRef.
- Q. Wang, Y. Xu, R. Lou, Z. Liu, M. Li, Y. Huang, D. Shen, H. Weng, S. Wang and H. Lei, Nat. Commun., 2018, 9, 3681 CrossRef PubMed.
- T. Brumme, M. Calandra and F. Mauri, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 245406 CrossRef.
- Y. Miura and K. Masuda, Phys. Rev. Mater., 2021, 5, L101402 CrossRef CAS.
- S. Sinha, P. C. Adak, A. Chakraborty, K. Das, K. Debnath, L. V. Sangani, K. Watanabe, T. Taniguchi, U. V. Waghmare and A. Agarwal, et al. , Nat. Phys., 2022, 18, 765–770 Search PubMed.
- T. Jungwirth, J. Wunderlich and K. Olejník, Nat. Mater., 2012, 11, 382–390 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02528h |
| ‡ Ez: Electric field along the z-direction. |
| This journal is © The Royal Society of Chemistry 2025 |