Direct determination of multiphoton absorption cross-sections by transient absorption spectroscopy

Abstract

Single- and multi-photon absorption cross-sections quantify the likelihood that a material will absorb one or more photons at a given wavelength. This critical parameter is fundamental to understanding light-matter interactions that underpin key applications in spectroscopy, photochemistry and advanced imaging techniques like multi-photon microscopy and deep tissue imaging. Conventional methods for measuring absorption cross-sections are often limited by sensitivity to sample morphology, type, concentration, and high excitation intensities – factors that can compromise reliability, increase experimental complexity, and risk sample damage. Herein, we present a direct, robust, and versatile method for quantifying absorption cross-sections across single- to multi-photon regimes, based on the saturation behaviour of transient absorption signals. Using this approach, we report for the first time the three-photon and four-photon absorption cross-sections of CsPbI₃ perovskite nanocrystals and CdSe/ZnS quantum dots under 1700 nm and 2100 nm excitation. These values exceed those of incumbent materials used for mouse deep-brain imaging by at least an order of magnitude. Our method does not rely on photoluminescence signals, making it suitable for weakly or non-emissive materials. Importantly, our work provides a powerful generalizable tool to accelerate the discovery and optimization of next generation photon-harvesting materials.

---

Introduction

Single-photon and multi-photon harvesting materials are crucial for advancements in diverse fields of energy sustainability,^1,2 environmental remediation,³ quantum technologies,⁴ and biomedicine.^5,6 These materials form the foundation for light energy utilization and conversion, with their performance directly influencing the efficiency, stability, and range of applications for related technologies. A key factor in these applications is the average number of excitons generated per material unit under a given light excitation intensity (〈n〉), which determines critical properties such as energy conversion efficiency,⁷ quantum coherence,⁸ and material/device stability.⁹ This value is intrinsically tied to the absorption cross-section (σ_n) and excitation flux,¹⁰ making accurate determination essential for optimizing material functionality. As such, the σ_n of single-photon and multiphoton processes are vital spectroscopic parameters for light/photon harvesting materials. Developing a direct, reliable, and accessible method for measuring these parameters in a broad range of materials is crucial to advancing material research and accelerating the development of transformative technologies.

Traditionally, single-photon absorption cross-sections are determined using UV-Vis spectroscopy and often require additional information on the size, shape, and elemental composition of the sample. However, this becomes challenging for nanomaterials with intricate architectures and heterogeneous compositions.¹¹ Multiphoton absorption (MPA) cross-sections (MPACSs) are typically measured using open-aperture Z-scan or static intensity-dependent transmission (SIDT). These methods require high excitation intensities, which can potentially damage the sample and introduce artifacts, especially for higher-order MPA measurements.¹⁰ The indirect multiphoton excitation (MPE) photoluminescence (PL) ratio method offers greater sensitivity, but relies on accurate reference parameters and strong PL signals. Thus it is unsuitable for weakly- or non-emissive materials.¹² These methods also require precise knowledge of the material concentration, which is difficult for quantum dots and nanocrystals. Transient PL intensity saturation method circumvents the need for morphology or concentration data. However, it was developed to measure single-photon absorption cross-sections,¹³ and is again unsuitable for weakly- or non-emissive materials. Furthermore, its accuracy also varies with the type of materials.

Of late, the transient absorption (TA) saturation method has been demonstrated as a reliable complementary approach for measuring single-photon absorption cross-sections without requiring additional information on the material morphology, volume, or concentration.^11,14 Here, we extend this method to enable direct, reliable, and convenient measurement of absorption cross-sections of multi-photon processes. Using this approach, we characterized CsPbI₃ perovskite NCs and commercial red-emitting CdSe/ZnS QDs, both of which hold significant potential for high-order multi-photon applications. For the first time, we report their three-photon (1700 nm) and four-photon (2100 nm) absorption cross-sections: (25 ± 2) × 10⁻⁷⁶ cm⁶ s² photons⁻² and (3.4 ± 0.1) × 10⁻⁷⁶ cm⁶ s² photons⁻² for 3PA, and (21 ± 2) × 10⁻¹⁰⁷ cm⁸ s³ photons⁻³ and (4.6 ± 0.6) × 10⁻¹⁰⁷ cm⁸ s³ photons⁻³ for 4PA, respectively, which are at least one order higher than those of aggregation induced-emission (AIE) dots and commercial Qtracker QDs used in deep-brain imaging. We also evaluated the measurement boundaries of the method, demonstrating its applicability to most advanced photon-harvesting materials and offering insights for further improvement. Notably, this TAS-based approach does not require a tight-focusing geometry for techniques like Z-scan, thereby suppressing higher-order nonlinear contributions. Moreover, this approach does not rely on the detection of PL signals, making it applicable for weakly- or non-emissive materials.

TAS setup and analysis for single-/multi-photon excitation

Fig. 1 shows the transient absorption spectroscopy (TAS) setup with different pump wavelengths from 400 nm to 2100 nm for single-photon to multi-photon absorption cross-sections measurements (see Experimental sections (ESI)† for detailed description). Under single-photon excitation (SPE) or multi-photon excitation (MPE), the pseudo-colour TA contour plots (Fig. S1a–d and S2a–d†) exhibit a dominant photobleaching signal originating from state-filling of the single excitons under long pump-probe delay times (Fig. S3 and Table S3†). We hypothesize that by monitoring the state-filling, a given multiphoton absorption process when corrected for the photon fluence and absorption cross-section can be considered as equivalent to a single-photon absorption process that generates the same average number of excitons (Fig. 2). By analysing the bleaching signal |ΔOD(t_l)| at the exciton absorption peak in the TA data of an optically dilute sample at a sufficiently long pump-probe delay time (t_l), we can use the Poisson distribution¹¹ to describe the related dynamical processes following SPE/MPE:

|ΔOD(t_l)| = a(1 − e^{−〈N(t)〉}) (1)

where a is a constant that is related to instrumental (e.g., optical path and focusing geometry) and sample parameters, which may differ when measuring different samples or photon absorption process of different orders. 〈N(t)〉 refers to the average number of excitons generated per NC/QD at a given pump photon flux (F(t)) upon SPE/MPE (per event):where σ_n (n = 1, 2, 3, 4, 5, etc.) refers to the single-/multi-photon absorption cross-section (in cm²ⁿ sⁿ⁻¹ photons¹⁻ⁿ), and f is the pulse repetition rate. We note that 〈N(t)〉 is proportional to 〈Fⁿ(t)〉, not 〈F(t)〉ⁿ.¹⁵ However, most detectors give only a signal that is proportional to 〈F(t)〉, we thus rewrite eqn (2) in terms of the average pump photon flux:where g⁽ⁿ⁾ = 〈Fⁿ(t)〉/〈F(t)〉ⁿ is a measure of the n^th order temporal coherence of the excitation source. Defining τ as the excitation pulse width (see details in Fig. S4, S5 and ESI†)^16,17 and fτ as the duty cycle, we can express g⁽ⁿ⁾ in terms of a dimensionless quantity g_p⁽ⁿ⁾ depending on the temporal profile of the excitation pulse:

g⁽ⁿ⁾ = g_p⁽ⁿ⁾/(fτ)ⁿ⁻¹ (4)

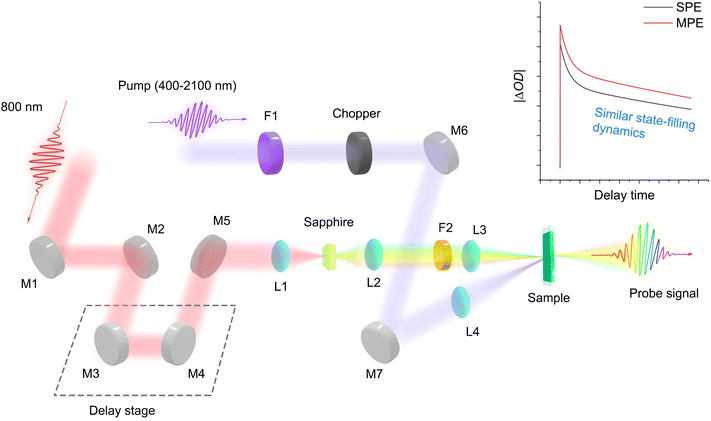Fig. 1 Transient absorption spectroscopy setup for photon absorption cross-sections measurements. The probe signal is collected by a spectrometer. M: mirror; L: lens; F: filter. SPE: single-photon excitation. MPE: multi-photon excitation. The main idea behind the approach is based on changes in absorption measured by the probe pulse resulting from the state-filling of the same excited state regardless of SPE/MPE.

Fig. 2 Schematic illustration of the multi-photon absorption, equivalent exciton generation and exciton recombination processes. Since both single-photon and multi-photon absorption lead to exciton formation at the same excited state, we posit that a given multiphoton absorption process when corrected for the photon fluence and absorption cross-section can be considered as equivalent to a single-photon absorption process that generates the same average number of excitons or the filling of the lowest excited state. CB: conduction band; VB: valence band; S₀: ground state; S₁: 1st excited state; S_n: higher energy n^th excited state.

For an excitation pulse with a Gaussian temporal profile, we can calculate that g_p⁽¹⁾ = 1, g_p⁽²⁾ = 0.664, g_p⁽³⁾ = 0.51, g_p⁽⁴⁾ = 0.415, and g_p⁽⁵⁾ = 0.348, etc. In addition, using F(t) = J(t) × f in which J(t) is the photon fluence, eqn (3) can then be rewritten as:

We define , where J⁽ⁿ⁾ refers to the photon fluence (PF) for single-photon excitation (n = 1), or equivalent photon fluence (EPF) for multi-photon excitation (n > 1). By plotting J⁽ⁿ⁾ and |ΔOD(t_l)| and fitting the data using eqn (1), the value of σ_n can be derived. This direct state-filling approach for determining the single-/multi-photon absorption cross-sections does not require information such as the size and concentration of NCs/QDs.

Cross-section measurements

To test our approach, we used promising emergent MPA materials, i.e., halide perovskite CsPbI₃ NCs as well as commercially available core/shell CdSe/ZnS QDs as representative samples because of their high nonlinear optical properties and red emission potentially suitable for bioimaging.^18–20 Basic spectral and structural information of these two materials are shown in Fig. 3a, S6a and b.† The parameters obtained (e.g., absorption and emission bands, PLQY (η), crystal morphology, etc.) are comparable to those reported in the literature.^21,22 Using 800 nm excitation of CsPbI₃ NCs as an example (Fig. 3b), the bleaching signal associated with single exciton recombination at long delay time and the width of the pump pulse are essential information for fitting the MPACSs, which can be extracted from the 2D TA spectrum. Fig. S1e–h and S2e–h† show the saturation trend of the TA spectral bleaching signal under single-photon (400 nm) to multi-photon (800–2100 nm) excitation with increasing pump fluence, which can be well-fitted by eqn (1) to determine the single-photon to 4-photon absorption cross-sections as shown in Fig. 3c–f, S6c–f, Tables S1 and S2.†

Fig. 3 Single-photon and multi-photon absorption cross-sections of CsPbI₃ nanocrystals. (a) Absorption and photoluminescence (PL) spectra of CsPbI₃ NCs in toluene. Insets: (lower left) Images of CsPbI₃ NCs in toluene under bright field (BF) and photoluminescence (PL) upon 365 nm excitation. (upper right) High-resolution transmission electron microscopy (HRTEM) images of CsPbI₃ NCs, showing the average size is ∼10 nm. Scale bar, 20 nm. (b) Single exciton participation related bleaching signal and cross correlation non-resonant electronic response signal extracted from the 2D pseudo-colour TA spectrum. We used 800 nm excited TA spectrum as an example. (c–f) |ΔOD| as the function of photon fluence (PF) for 400 nm excitation (c) or equivalent photon fluence (EPF) for multiphoton excitation at 800 nm in (d), 1700 nm in (e) and 2100 nm in (f) at the delay time of 1000 ps. The solid curves are the best fit to eqn (1), which are used to derive the linear/nonlinear absorption cross-sections. (g and h) State-of-the-art promising fluorescence probes with large 3-photon (g) and 4-photon (h) action cross-sections for mouse deep brain imaging.

The measured single- (400 nm) and 2-photon (800 nm) absorption cross-sections of CsPbI₃ NCs (size of ∼10 nm) and CdSe/ZnS QDs (size of ∼5 nm) are in good agreement with values reported previously.^13,23,24 Using our method, we also characterized the two-photon absorption cross-section of MAPbBr₃ NCs synthesized using a literature-reported procedure.¹² Under 800 nm excitation, we obtained a value of (7.4 ± 0.8) × 10⁵ GM (Fig. S7†), which closely matches the value of ∼8 × 10⁵ GM reported using open-aperture Z-scan, thereby confirming the reliability of our TA-based approach. For high-order multiphoton excitation (n ≥ 3), we report for the first time the MPACSs of CsPbI₃ NCs and II–VI type CdSe/ZnS QDs: (25 ± 2) × 10⁻⁷⁶ cm⁶ s² photons⁻² and (3.4 ± 0.1) × 10⁻⁷⁶ cm⁶ s² photons⁻² for 3-photon excitation (1700 nm), and (21 ± 2) × 10⁻¹⁰⁷ cm⁸ s³ photons⁻³ and (4.6 ± 0.6) × 10⁻¹⁰⁷ cm⁸ s³ photons⁻³ for 4-photon excitation (2100 nm), respectively. Current research on red-emissive probes primarily focuses on 2-photon and 3-photon fluorescence applications as their excitation wavelengths falls within the NIR-II (1100–1350 nm) and NIR-III (1600–1870 nm) windows that are optimal for bioimaging.²⁵ In bioimaging, an important parameter characterizing MPE fluorescence brightness is the multiphoton action cross-section (σ_n × η). Given the near unity PLQY of our CsPbI₃ NCs, the measured three-photon action cross-section at 1700 nm excitation (i.e., the optimal window for deep brain imaging¹⁰) is ∼6 orders of magnitude higher than that of the commonly used organic dye Rhodamine 6G (R6G)²⁶ and ∼4 orders of magnitude higher than that of advanced AIE DCBT organic dots previously applied in mouse brain vasculature imaging (Fig. 3g).²⁷ For four-photon (and higher-order) fluorescence applications, excitation can occur within the NIR-IV (2100–2300 nm) window, which still allows for deep brain imaging.²⁸ However, the imaging quality and depth are currently limited by the available excitation power in this range as well as at longer wavelengths. Additionally, sample damage thresholds impose further limitations on the excitation power that can be used. Notably, our measured four-photon action cross-sections of CdSe/ZnS QDs and CsPbI₃ NCs are 1–2 orders of magnitude higher than the best values currently used for deep brain imaging (Fig. 3h), suggesting a promising potential to improve the imaging depth and quality despite the limitations in excitation power and sample damage threshold.

Measurement boundaries

When testing the low absorption band of the standard dye molecule Rhodamine B (RhB) at 400 nm, we found that even with an extremely high pump power (>1.7 mJ cm⁻²), the TA bleaching signal could not reach saturation. Consequently, its absorption cross-section at 400 nm could not be directly obtained (Fig. S8†). This prompted us to further investigate the measurement boundaries of absorption cross-sections using the TAS method. The measurement range is inherently constrained by the available optical power of the laser in the setup. However, we found that even with sufficiently high pump power, any further increase beyond a specific threshold triggers an unstable nonlinear optical (NLO) phenomenon in the sample holder, which disrupts the measurements and prevents further data collection. Typically, under 800 nm femtosecond laser excitation, when the pump power density exceeds approximately 10.2 mJ cm⁻², the synthetic quartz cuvette (Glass Micro Cuvette, 700 μL, Thorlabs) exhibits concentric, broadband NLO bright spots (Fig. S9†). After passing through optical filters, these spots manifest as orange-red emission with irregular spectra spanning approximately 500–750 nm (Fig. 4a and b). We systematically determined the NLO generation thresholds for pump wavelengths spanning from 400 nm to 2100 nm, yielding values of 4.1 mJ cm⁻² at 400 nm, 10.2 mJ cm⁻² at 800 nm, 29.4 mJ cm⁻² at 1200 nm, 81.6 mJ cm⁻² at 1700 nm, and 191.1 mJ cm⁻² at 2100 nm, respectively (Fig. 4c). Interestingly, a linear correlation was observed between the logarithm of these threshold values and the corresponding pump wavelengths. This may be because the NLO generation driven by multiphoton absorption created free-electron plasma²⁹ requires a threshold fluence inversely proportional to an absorption cross-section that itself decreases exponentially with photon-orders (wavelength). Assuming these pump fluence thresholds represent the upper limits for achieving saturated TA bleaching signals, we modelled and fitted the data using eqn (1) to estimate the measurable σ_n(λ) (n = 1, 2, 3, 4 and 5; λ = 400 nm, 800 nm, 1200 nm, 1700 nm, and 2100 nm) thresholds (Fig. 4d and S10–S14†). Our analysis revealed that, for the same photon absorption process, the logarithm of the σ_n(λ) thresholds also exhibit a linear relationship with the corresponding pump wavelengths. By fitting this relationship, the measurement boundaries of the system for single-photon and higher-order multiphoton absorption cross-sections can be determined. Fig. 4e illustrates the measurement boundaries of the system for absorption cross-sections ranging from single-photon to five-photon processes. These boundaries encompass the requirements of most advanced single-photon and multiphoton-harvesting materials, including dye molecules,^30,31 AIE dots,^27,32 metal–organic frameworks (MOFs) and their hybrid materials,^33,34 II–VI and III–V quantum dots,^26,35–40 commercial Qtracker quantum dots,²⁸ and perovskite nanocrystals,^11–13,41etc. This highlights the versatility and universality of the TAS-based method for unified measurements of single-photon and multiphoton absorption cross-sections.

Fig. 4 Measurement boundaries of the system. (a and b) Spectra (a) and images (b) of the quartz cuvette (containing toluene) under 800 nm excitation with pump fluence below/beyond the nonlinear optics (NLO) generation threshold of ∼10.2 mJ cm⁻². The 800 nm excitation was blocked by filters before spectral collection. (c) Thresholds of the NLO generation process of the quartz cuvette upon representative excitation of 400 nm, 800 nm, 1200 nm, 1700 nm and 2100 nm. (d) The process of estimating the threshold and boundary of the single/multi-photon absorption cross section (σ_n, n = 1, 2, 3, 4 and 5) that can be measured by the system. (e) Calculated measurable σ_n boundaries of the system (the vertical axis represents the logarithm of σ_n) and state-of-the-art σ_n of existing materials, demonstrating the universality of our measurement system.

Conclusions

We have developed a straight-forward transient absorption spectroscopy (TAS)-based method for measuring the photon absorption cross-sections of materials universally applicable for single-photon to multi-photon absorption measurements. For the first time, we determined the absorption cross-sections up to four-photon processes (2100 nm excitation) in promising multiphoton imaging materials, CsPbI₃ NCs and CdSe/ZnS QDs. We evaluated the measurement boundaries of the proposed method, revealing that it sufficiently meets the requirements of most state-of-the-art photon-harvesting materials. Furthermore, the theoretical framework of our method can be readily extended to higher-order absorption process (e.g., six-photon or beyond). In this study, derivations were demonstrated up to five-photon absorption, aligning with the current state-of-the-art.¹² From the perspective of measurement feasibility, universality, and the extension of high-order multiphoton technologies, we identify the following areas for improvement: (1) enhancing laser power in the short-wave infrared region (1000–3000 nm):⁴² For instance, measuring the five-photon absorption of CsPbI₃ NCs may require a pump fluence exceeding 350 mJ cm⁻² with femtosecond laser excitation near 2800 nm. (2) Improving sample holder materials: materials with higher damage thresholds and the ability to suppress nonlinear optical effects under high pump fluence could further expand the measurement boundaries of the proposed method. For instance, sapphire shows an NLO threshold exceeding 0.9 J cm⁻² at 1053 nm (ref 43) – far above the roughly 20 mJ cm⁻² threshold of quartz cuvette, which will significantly lower the minimum measurable limit. Our work not only deepens the understanding of photon-harvesting behaviors but also provides a more direct and accessible approach for multi-photon absorption cross-section measurements.

Data availability

All data are available in the main text and the ESI† or openly available in DR-NTU at https://doi.org/10.21979/N9/DZRHSQ.

Author contributions

Huajun He: conceptualization, analysis, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing; Jia Wei Melvin Lim: investigation, writing – review & editing; Minjun Feng: investigation, writing – review & editing; Zengshan Xing: investigation, writing – review & editing; Tze Chien Sum: conceptualization, funding acquisition, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Ministry of Education under its AcRF Tier 1 grant (RG152/24) and AcRF Tier 2 grant (MOE-T2EP50123-0001) and the National Research Foundation (NRF) Singapore under its Competitive Research Programme (NRF-CRP25-2020-0004).

Notes and references

1. J. Han, K. Park, S. Tan, Y. Vaynzof, J. Xue, E. W.-G. Diau, M. G. Bawendi, J.-W. Lee and I. Jeon, Nat. Rev. Method. Prime., 2025, 5, 3.
2. A. H. Proppe, Y. C. Li, A. Aspuru-Guzik, C. P. Berlinguette, C. J. Chang, R. Cogdell, A. G. Doyle, J. Flick, N. M. Gabor, R. van Grondelle, S. Hammes-Schiffer, S. A. Jaffer, S. O. Kelley, M. Leclerc, K. Leo, T. E. Mallouk, P. Narang, G. S. Schlau-Cohen, G. D. Scholes, A. Vojvodic, V. W.-W. Yam, J. Y. Yang and E. H. Sargent, Nat. Rev. Mater., 2020, 5, 828–846.
3. M. Q. Yang, M. Gao, M. Hong and G. W. Ho, Adv. Mater., 2018, 30, e1802894.
4. F. Hu, H. Zhang, C. Sun, C. Yin, B. Lv, C. Zhang, W. W. Yu, X. Wang, Y. Zhang and M. Xiao, ACS Nano, 2015, 9, 12410–12416.
5. E. E. Hoover and J. A. Squier, Nat. Photon., 2013, 7, 93–101.
6. B. Zhou, B. Shi, D. Jin and X. Liu, Nat. Nanotech., 2015, 10, 924–936.
7. Y. Wang, S. Ye, J. W. M. Lim, D. Giovanni, M. Feng, J. Fu, H. N. S. Krishnamoorthy, Q. Zhang, Q. Xu, R. Cai and T. C. Sum, Nat. Commun., 2023, 14, 6293.
8. A. Ishizaki and G. R. Fleming, Annu. Rev. Condens. Matter Phys., 2012, 3, 333–361.
9. S. Kundu and A. Patra, Chem.Rev., 2017, 117, 712–757.
10. H. He and T. C. Sum, Dalton Trans., 2020, 49, 15149–15160.
11. J. Puthenpurayil, O. H. Cheng, T. Qiao, D. Rossi and D. H. Son, J. Chem. Phys., 2019, 151, 154706.
12. W. Chen, S. Bhaumik, S. A. Veldhuis, G. Xing, Q. Xu, M. Grätzel, S. Mhaisalkar, N. Mathews and T. C. Sum, Nat. Commun., 2017, 8, 15198.
13. N. S. Makarov, S. Guo, O. Isaienko, W. Liu, I. Robel and V. I. Klimov, Nano Lett., 2016, 16, 2349–2362.
14. M. Ji, S. Park, S. T. Connor, T. Mokari, Y. Cui and K. J. Gaffney, Nano Lett., 2009, 9, 1217–1222.
15. C. Xu and W. W. Webb, J. Opt. Soc. Am. B, 1996, 13, 481–491.
16. M. Feng, S. Ye, J. W. M. Lim, Y. Guo, R. Cai, Q. Zhang, H. He and T. C. Sum, Small, 2023, 19, 2301831.
17. J. W. M. Lim, Y. Guo, M. Feng, R. Cai and T. C. Sum, J. Am. Chem. Soc., 2024, 146, 437–449.
18. J. Xu, X. Li, J. Xiong, C. Yuan, S. Semin, T. Rasing and X. H. Bu, Adv. Mater., 2020, 32, e1806736.
19. M. Sohail, X. Shen, I. Alam, Z. Ali, N. Razzaq and Q. Ouyang, ACS Appl. Nano Mater., 2024, 7, 22766–22778.
20. H. Pan, H. Chu, Y. Li, N. Qi, S. Zhao, G. Li and D. Li, Nanotechnology, 2020, 31, 195703.
21. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
22. A. Makhal, H. Yan, P. Lemmens and S. K. Pal, J. Phys. Chem. C, 2010, 114, 627–632.
23. Z. Cao, B. Lv, H. Zhang, Y. Lv, C. Zhang, Y. Zhou, X. Wang and M. Xiao, J. Chem. Phys., 2019, 151, 154201.
24. S. Masuo, H. Naiki, S. Machida and A. Itaya, Appl. Phys. Lett., 2009, 95, 193106.
25. Y. Chen, Mater. Today Chem., 2022, 25, 100975.
26. G. Xing, S. Chakrabortty, S. W. Ngiam, Y. Chan and T. C. Sum, J. Phys. Chem. C, 2011, 115, 17711–17716.
27. Z. Zheng, H. Zhang, H. Cao, J. Gong, M. He, X. Gou, T. Yang, P. Wei, J. Qian, W. Xi and B. Z. Tang, ACS Nano, 2022, 16, 6444–6454.
28. S. Tong, J. Zhong, X. Chen, X. Deng, J. Huang, Y. Zhang, M. Qin, Z. Li, H. Cheng, W. Zhang, L. Zheng, W. Xie, P. Qiu and K. Wang, ACS Nano, 2023, 17, 3686–3695.
29. A. Dubietis and A. Couairon, Ultrafast supercontinuum generation in transparent solid-state media, Springer, 2019.
30. Y. Jiang, K. F. Li, K. Gao, H. Lin, H. L. Tam, Y. Y. Liu, Y. Shu, K. L. Wong, W. Y. Lai, K. W. Cheah and W. Huang, Angew. Chem., Int. Ed., 2021, 60, 10007–10015.
31. L. Zhang, M. Morshedi and M. G. Humphrey, Angew. Chem., Int. Ed., 2022, 61, e202116181.
32. S. Wang, X. Li, S. Y. Chong, X. Wang, H. Chen, C. Chen, L. G. Ng, J. W. Wang and B. Liu, Adv. Mater., 2021, 33, e2007490.
33. R. Medishetty, L. Nemec, V. Nalla, S. Henke, M. Samoc, K. Reuter and R. A. Fischer, Angew. Chem., Int. Ed., 2017, 56, 14743–14748.
34. H. He, Y. Cui, B. Li, B. Wang, C. Jin, J. Yu, L. Yao, Y. Yang, B. Chen and G. Qian, Adv. Mater., 2019, 31, e1806897.
35. Y. Gao, A. Tonizzo, A. Walser, M. Potasek and R. Dorsinville, Appl. Phys. Lett., 2008, 92, 033106.
36. A. D. Lad, P. Prem Kiran, G. Ravindra Kumar and S. Mahamuni, Appl. Phys. Lett., 2007, 90, 133113.
37. C. A. Leatherdale, W. K. Woo, F. V. Mikulec and M. G. Bawendi, J. Phys. Chem. B, 2002, 106, 7619–7622.
38. C. de Mello Donegá and R. Koole, J. Phys. Chem. C, 2009, 113, 6511–6520.
39. D. V. Talapin, N. Gaponik, H. Borchert, A. L. Rogach, M. Haase and H. Weller, J. Phys. Chem. B, 2002, 106, 12659–12663.
40. I. Moreels, K. Lambert, D. Smeets, D. De Muynck, T. Nollet, J. C. Martins, F. Vanhaecke, A. Vantomme, C. Delerue, G. Allan and Z. Hens, ACS Nano, 2009, 3, 3023–3030.
41. J. Li, C. Ren, X. Qiu, X. Lin, R. Chen, C. Yin and T. He, Photon. Res., 2018, 6, 554–559.
42. F. Ren, F. Wang, A. Baghdasaryan, Y. Li, H. Liu, R. Hsu, C. Wang, J. Li, Y. Zhong, F. Salazar, C. Xu, Y. Jiang, Z. Ma, G. Zhu, X. Zhao, K. K. Wong, R. Willis, K. Christopher Garcia, A. Wu, E. Mellins and H. Dai, Nat. Biomed. Eng., 2024, 8, 726–739.
43. T. Imran and G. Figueira, J. Optics, 2012, 14, 035201.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc03392f

---