We consider elastic microfilaments which form closed loops. We investigate how the loops change shape and orientation while settling under gravity in a viscous fluid. Loops are circular at the equilibrium. Their dynamics are investigated numerically based on the Stokes equations for the fluid motion and the bead–spring model of the microfilament. The Rotne–Prager approximation for the bead mobility is used. We demonstrate that the relevant dimensionless parameter is the ratio of the bending resistance of the filament to the gravitation force corrected for buoyancy. The inverse of this ratio, called the elasto-gravitation number 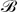, is widely used in the literature for sedimenting elastic linear filaments. We assume that 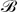is of the order of 10⁴–10⁶, which corresponds to easily deformable loops. We find out that initially tilted circles evolve towards different sedimentation modes, depending on 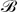. Very stiff or stiff rings attain almost planar, oval shapes, which are vertical or tilted, respectively. More flexible loops deform significantly and converge towards one of several characteristic periodic motions. These sedimentation modes are also detected when starting from various shapes, and for different loop lengths. In general, multi-stability is observed: an elastic ring converges to one of several sedimentation modes, depending on the initial conditions. This effect is pronounced for very elastic loops. The surprising diversity of long-lasting periodic motions and shapes of elastic rings found in this work gives a new perspective for the dynamics of more complex deformable objects at micrometer and nanometer scales, sedimenting under gravity or rotating in a centrifuge, such as red blood cells, ring polymers or circular DNA.