Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pulsed laser polymerization to retrieve kinetic parameters for a propagated mid-chain radical in poly(n-butyl acrylate) synthesis: a combined DFT and kinetic Monte Carlo study†
F. A. Lugob,
L. Trossaertab,
Y. W. Marien ac,
M. K. Sabbe
ac,
M. K. Sabbe a,
M. Edeleva
a,
M. Edeleva b,
D. R. D'hooge
b,
D. R. D'hooge *ad and
P. H. M. Van Steenberge
*ad and
P. H. M. Van Steenberge a
a
aLaboratory for Chemical Technology (LCT), Ghent University, Technologiepark 125, B-9052 Gent, Belgium. E-mail: dagmar.dhooge@ugent.be
bCentre for Polymer and Material Technologies (CPMT), Ghent University, Technologiepark 130, B-9052 Gent, Belgium
cIntelligence in Processes, Advanced Catalysts and Solvents (iPRACS), Faculty of Applied Engineering, University of Antwerp, Groenenborgerlaan 171, 2020 Antwerp, Belgium
dCentre for Textile Science and Engineering (CTSE), Ghent University, 70a, B-9052 Gent, Belgium
First published on 30th June 2025
Abstract
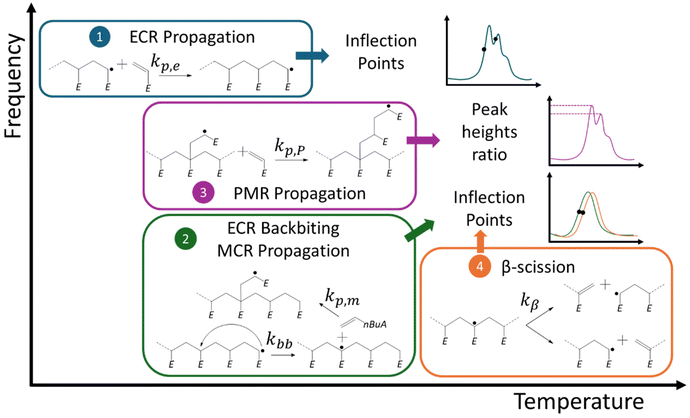
Radical polymerization of n-butyl acrylate is characterized by backbiting of end-chain radicals (ECRs), with a propagation rate coefficient kp,e, into mid-chain radicals (MCRs), with a propagation rate coefficient kp,m. In pulsed laser polymerization (PLP) kinetic studies, it is currently assumed that a MCR becomes a (fully developed) ECR after one propagation step. Here we demonstrate that a more gradual transition likely takes place, introducing a propagated mid-chain radical (PMR) with a propagation rate coefficient kp,P or equivalently a transition propagation factor γ that at least theoretically can vary between 0 (kp,P = kp,m) and 1 (kp,P = kp,e). Kinetic Monte Carlo (kMC) simulations under free radical polymerization (FRP) conditions hint at a γ not too close to 0 (e.g. not below 0.01), and Density functional theory (DFT) calculations at a γ not too close to 1 (e.g. not above 0.8). It is further shown that the ratio of the peak heights in a PLP – size exclusion chromatography (PLP-SEC) spectrum is sensitive to a variation in γ. This opens the door to the future experimental determination of kp,P considering different frequencies, provided that the initiator radical generation is well-described. At 325 K and using 500 Hz literature data, we currently put forward a γ of 0.1. In addition, the PMR backbiting potential is evaluated, introducing a backbiting scaling factor δ with respect to the conventional ECR backbiting rate coefficient (kbb). It is showcased that this extra backbiting contributes to a better understanding of the migration mechanism and short branch formation in acrylate radical polymerization, although the experimental determination of δ is less straightforward. Overall the current work highlights how acrylate-specific rate coefficients can be obtained in a roadmap format, considering higher and lower frequencies, and lower and higher temperatures.
Introduction
Free radical polymerization (FRP) is a widely used technique for the production of polyacrylics such as polyacrylates.1–5 Such polymers are nowadays manufactured using a large variety of (co)monomers, both fuel- and biomass-based, making them very suitable for material optimization and property tuning.1,6–12 However, for a given polyacrylate to suit a certain application, a proper tuning of the molecular properties (e.g. molar mass distribution (MMD) or branching level) is desired. This is non-trivial as polyacrylate synthesis displays a complicated reaction scheme, dealing with multiple secondary reactions next to the conventional FRP reactions, e.g. initiation, (secondary) propagation, and termination. A detailed mechanistic understanding of acrylate polymerization is thus not straightforward and kinetic modeling is a desired pathway, provided that the (intrinsic) rate coefficients of all kinetically relevant reactions are carefully determined.13–17A well-established technique for the determination of rate coefficients in radical polymerization is pulsed laser polymerization (PLP) in combination with size exclusion chromatography (SEC).18 Aleksandrov et al.19 originally studied kinetic and MMD variations in PLP. Later on Olaj et al.20 extended the technique to obtain the propagation rate coefficient from the log-MMD. Additionally, the technique is recommended by the IUPAC Subcommittee on Modeling of Polymerization Kinetics and Processes.21–27
PLP employes a laser beam to create pulse-wise initiator radicals, most commonly 2,2-dimethoxy-2-phenylacetophenone (DMPA) fragments, that initiate radical chain growth.28,29 During the time between two laser pulses, which is called the dark time Δt, (macro)radicals grow and some of them terminate at the next pulse via the freshly generated initiator fragments in a kind of quenching manner.30
If only a (conventional) end-chain radical (ECR) is active as a macroradical in a PLP experiment, the chain length of specific dead polymer species (Lj) will therefore depend on the number of pulses (j), Δt, the initial monomer concentration ([M]0), and the ECR propagation rate coefficient kp,e:
| Lj = kp,e[M]0(jΔt). | (1) |
Practically, L1 is the first inflection point (or peak maximum) of the SEC trace (j = 1),31–35 and L2 provides a consistency check because it needs to be equal to twice L1.21,36
In general, the subscript “app” should be used in eqn (1) to highlight that several macroradical types can exist, each with a distinct (intrinsic) propagation reactivity, together leading to an observed thus lumped/apparent propagation reactivity (kp,app). For example, in high temperature acrylate radical polymerization kp,app does not equal kp,e. Mid-chain radicals (MCRs) are then also present, undergoing slower (tertiary) propagation (rate coefficient: kp,m). Mechanistically, the formation of MCRs out of ECRs mainly proceeds through intramolecular chain transfer, i.e. backbiting. This reaction proceeds most easily via a six-membered transition state, leading to the creation of polymer chains with short side chain branches upon further (tertiary) propagation.37–40
The existence of ECRs and MCRs (top of Fig. 1) in acrylate radical polymerization moves the SEC trace to the lower chain length region, due to a lower kp,m,40–47 which can be understood considering the bulkier and more carbon substituted nature of the MCR and the difference in stability between both radical types. In other words, whenever backbiting occurs and a MCR is formed, a decrease of kp,app takes place because a MCR propagates at a slower rate.17 At sufficiently high temperatures macromonomers are also formed, due to fragmentation (β-scission) of MCRs.48,49
Notably, the influence of certain secondary reactions such as backbiting can be minimized by adapting the PLP conditions. A low temperature and high laser pulse frequency enable for instance an accurate (isolated) determination of kp,e, as highlighted by Willemse and van Herk,50 who studied the secondary propagation of methyl, ethyl, butyl, hexyl and benzyl acrylate at frequencies between 60 and 100 Hz and temperatures between −25 to 37 °C. Even higher frequencies, i.e. 500 Hz and 1 kHz, have been used for PLP of n-butyl acrylate by Barner-Kowollik et al.30 and Wenn and Junkers51 respectively. Once kp,e is known, a stepwise modification of the (isothermal) PLP conditions can be done to determine other (secondary) rate coefficients ideally one by one, enabling to span a detailed reaction scheme.30,43,52,53
Recent work by Marien et al.54 and Vir et al.18 showed that the rate coefficients for backbiting, MCR propagation and β-scission can be determined through stepwise PLP combined with kinetic Monte Carlo (kMC) simulations once kp,e is known. The first step consists of varying frequencies in the low frequency region (e.g. 10 to 50 Hz) at low to intermediate temperature while also varying the solvent fraction, selecting as solvent the saturated analogue of the monomer. Under these conditions β-scission is negligible, so that an isolation of the backbiting rate coefficient (kbb) and kp,m is possible. The second step follows the same procedure of varying frequencies and solvent fractions but deals with higher temperatures to determine the β-scission rate coefficient (kβ), inputting previously determined kp,e, kbb and kp,m values.
Another experimental technique commonly used for the determination of rate coefficients in radical polymerization is the combination of PLP with Electron Paramagnetic Resonance (PLP-EPR).55,56 This technique involves measuring the intensity of an EPR signal as a function of time, and from this, deducing concentration as a function of time for the radical species giving rise to the measured signal, whether it be ECR or MCR, both of which may be monitored simultaneously. The EPR measurement is often combined with PLP because it allows for control over the amount of radicals produced; specifically in certain cases authors used a single-pulse for these PLP-EPR experiments.57–68
Note that it is implicitly assumed in the current acrylate (PLP) modeling studies that a MCR becomes an ECR after one propagation step, although the computational chemistry work of Cuccato et al.69 for instance indicated a possible difference in propagation reactivity of a single-unit short branched polymer. Such difference has been related to the bulkier nature of the involved radical, in the current work denoted as a propagated mid-chain radical (PMR; Fig. 1; bottom left), as compared to a well-developed ECR, i.e. one possessing a radical center that is several monomer units away from the original MCR backbone. Similarly, chain length dependencies have been reported for the activation of halogen-capped tertiary radical chains in atom transfer radical polymerization (ATRP) involving methacrylates, due to an entropic strain effect.70 Also, for radical polymerizations with only ECRs, a different propagation rate coefficient for the first two to ten additions has been reported.71
In the present work, we enrich the PLP-SEC modeling analysis of acrylates by studying the kinetic and structural relevance of the transition from a MCR to a PMR, and this PMR to a (developed) ECR. We also perform density functional theory (DFT) simulations69,72–79 complementary with the work of Cuccato et al.,69 and we discuss PMR backbiting possibilities (new rate coefficient kbb,P), producing different types of branches and contributing to radical migration (Fig. 1; bottom right).
Practically, we calculate the PMR propagation rate coefficient, kp,P, using a transition propagation factor γ, and we calculate kbb,P via a scaling factor δ:
| kp,P = (kp,e − kp,m)γ + kp,m | (2) |
| kbb,P = δkbb | (3) |
Hence, for γ equal to 0, kp,P = kp,m results, for γ equal to 1 kp,P = kp,e (the current assumption), and for δ equal to 1 kbb,P = kbb.
A mechanistic foundation is put forward hinting at γ and δ values not being too close to 1, to then demonstrate that in future work γ could be experimentally determined by measuring peak height ratios in the PLP spectrum, taking into account a frequency variation and relying on a good determination of radical generation kinetic parameters (at lower temperatures). Focusing at FRP conditions, we also highlight that γ is (likely) sufficiently higher than 0 (e.g. ≫0.01), supporting current parameter tuning efforts from all IUPAC connected groups for kp,m and kbb ignoring the PMR species. Based on literature data at one frequency we assess γ as 0.1 at 325 K in the present work. For δ, however, only a rough estimate is possible in future work considering PLP branching data.
Overall this work contributes to the identification of a better roadmap for the determination of the (intrinsic) reactivities of acrylate specific reaction steps, and the type of branched species present. We complement the current modeling studies by a refinement of the kinetic scheme in case more detailed branching descriptions are aimed at.
Methods
Computational chemistry details
DFT calculations were performed using the Gaussian 16_C.01 package.80 The molecular model structures were optimized at the B3LYP/6-311+G(d,p) method and basis set. The thermal contributions were included using the harmonic oscillator approach at the same computational level. The structures used were confirmed to have zero imaginary frequencies for reactants and products, and one large imaginary frequency in the transition states. The prediction of the electronic energy was improved by using a single-point M06-2X/6-311+G(d,p) calculation employing the previously optimized geometries.To calculate enthalpies, entropies and free Gibbs energies in the gas phase, standard thermodynamic equations were used.81 Solvation effects were included using COSMO-RS theory82–84 to calculate the free Gibbs energy of solvation ΔGsolv, as implemented in the COSMOtherm software package.85 The COSMO-RS calculation uses the electronic energy calculated by BP86/TZVP single point calculations performed on the previously B3LYP/6-311+G(d,p) optimized geometry, using the density of nBua at 298 K of 894 g L−1.
The transition state theory (TST) was used to calculated the rate coefficients, using the free Gibbs reaction barrier including solvation effects:86,87
 | (4) |
 the temperature-dependent free Gibbs energy barrier, and R the universal gas constant.
the temperature-dependent free Gibbs energy barrier, and R the universal gas constant.
We calculated the propagation rate coefficient for PMR, kp,P, using the molecular model depicted in Fig. 2 (top). This model consists of a tetramer radical, which represents the intermediate between a MCR and ECR, propagating toward a monomer unit and forming the pentamer branched structure shown in Fig. 2 (top right). The use of multiple diastereomers, as incorporated in previous work, was unnecessary for this model, because the influence of the stereochemistry of adjacent units on the rate coefficient in propagation reactions is minimal.74 Furthermore, the computational effort, required to calculate the large structures of the model, can be significantly reduced by using a single diastereomer, making the calculations more feasible.
Similarly, the MCR propagation rate coefficient, kp,m, was calculated using the molecular model shown in Fig. 2 (bottom), which consist of a symmetric trimer nBuA structure with a radical in the middle unit, propagating towards a nBuA monomer. We employed a single diastereomer for this calculation, as the reaction represents an equivalent propagation process with no significant influence from the stereochemistry of adjacent units.
The rate coefficient for the ECR propagation, kp,e, was calculated using a model consisting of a unimer radical propagating towards a monomer nBuA unit.
Besides DFT analysis, it can be interesting to look at spectroscopic experimental techniques that can prove or measure details about the PMR radical. One technique could be EPR, which can detect different radicals within a system. However, the subtle structural difference between an ECR and a PMR might not be distinguishable by this technique, because in essence, both of these radicals are secondary radicals and the difference arises from the different nearby substituents. One can only hypothesize about which effect is greater than the other. In Kajiwara's work,89–91 the noisy spectrum at lower temperatures might be a result of the subtle differences between ECR and PMR, but nobody has looked for these species before because the PMR has not been discussed previously. Another technique might be detection by nuclear magnetic resonance (NMR). However, the applicability of this technique comes likely with various challenges because polymer samples produce a high signal-to-noise ratio, due to the existence of the large –CH2– signal. Hence, overall DFT is expected to be the easiest way to study the qualitative differences between ECR and PMR.
Kinetic Monte Carlo model details
For the prediction of the complete PLP-SEC trace and inflection point data, the previously developed kinetic Monte Carlo (kMC) model of our group was utilized as a starting point18,28,34,54 but including the two extra reactions with PMR via the already introduced formulas for γ and δ in the introduction (eqn (2) and (3)). It is important to mention that adding two extra parameters to a modelling system provides extra flexibility regarding the description of experimental data. However, both these parameters, γ and δ, are introduced to physically account for rate coefficients of species that likely have different reactivities because their chemical structures are different.The kMC model considers a detailed reaction scheme, accounting for chain length (and monomer conversion) dependent apparent termination reactivities with all kinetic parameters taken from the literature (with γ = 1). Under the conditions studied, namely a low temperature, a low monomer conversion and a high pulse rate, β-scission, macromonomer propagation and thermal self-initiation can be ignored.18
The Arrhenius parameters for termination (and chain transfer to monomer) with PMR are approximated as if the radical was an ECR. Fig. S1 of the ESI† shows that the impact of PMR-based radical termination over the polymer properties is limited within the expected theoretical limits, being defined by mutual ECR termination and mutual MCR termination, supporting this approximation. Additionally, any previous determination of termination reactivities might have clumped the effect of the PMR in the reported values, making the approximation of PMR reactivity as an ECR quite suitable. If the PMR termination kinetics would be of more relevance, the introduction of another type of radical would complicate further the determination of termination rate coefficients. However, this radical will not dominate the amount of radicals within the PLP so it is not kinetically relevant in the context of the present work.
Taking into account the decrease in light intensity along the optical path,92 the amount of radicals produced by photodissociation (ΔR0) is explicitly calculated:28,34,93,94
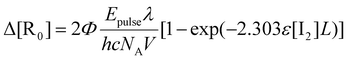 | (5) |
The kMC model simulates the PLP experiment, including a total number of 100 pulses and an additional consideration of 10 seconds of reaction until the quenching agent is introduced in line with Marien et al.34 The log-MMDs are corrected for SEC broadening, in agreement with work by Buback et al.103 (SEC broadening σvb = 0.042). Also here it is recommended to have this SEC broadening determined at lower temperatures where the effects of the PMR and MCR are irrelevant.
A Monte Carlo control volume of 10−14 L is considered to ensure convergence, considering previous work, optimizing the required simulation conditions to achieve the desired convergence in PLP simulations with many peaks and radical species.104,105
Results and discussion
In what follows, we first highlight that γ is likely not too close to 0 (e.g. not 0.01), by considering FRP simulations vs. typical experimental trends to then finetune that γ is likely also not too close to 1 (e.g. not 0.8), based on DFT calculations. We then propose a PLP-based method to determine γ with a first assessment of its value being 0.1 (325 K) based on literature data, to also formulate guidelines on the determination of acrylate specific rate coefficients in a roadmap format, including a focus on δ.Sensitivity analysis under FRP conditions: likely a γ value not too close to 0
For γ = 1, a PMR becomes an ECR and, hence, the original kMC model from our previous work results.18,28,34,54 For (solution) FRP conditions (333 K; AIBN as conventional initiator), this means variations for the monomer conversion, log-MMD, and MMD branching density at a monomer conversion of 0.9, as shown by the dark green lines/points in Fig. 3. | ||
| Fig. 3 kMC simulation of FRP of nBuA initiated by AIBN, considering the parameters in Table 1 for different values of γ (δ fixed at 1). (a) Monomer conversion vs time (h). (b) Log-MMD at a monomer conversion of 0.9. (c) Branching density at a monomer conversion of 0.9, defined as number of branches per monomer unit; 333 K and solvent fraction of 0.55; [AIBN]0 = 3 × 10−3 mol L−1. Green lines are realistic simulations so not too low γ values are expected (the currently accepted model is with γ = 1 and gives specifically the expected experimental variation in polymerization rate). In the current work we assess γ as 0.1 at 325 K, consistent with the statement of not too low γ values. | ||
| Nr | Reaction | Equation | A, L mol−1 s−1 or s−1 | Ea, kJ mol−1 | k@306 K, L mol−1 s−1 or s−1 | Ref. |
|---|---|---|---|---|---|---|
| a Initiator radicals (I and II) are different radicals created by the photodissociation of DMPA.34b For the FRP case, we use instead an initiator dissociation with the following kinetic parameters: A = 3.1 × 1015 s−1 and Ea = 131 kJ mol−1.98,99 For the PLP case the amount of initiator radicals produced by photodissociation in each laser pulse is calculated by eqn (5). Using λ = 351 × 10−9 m, Epulse = 2.5 × 10−3 J, V = 2 × 10−7 m3 and L = 5.2 × 10−3,34 Δ[R0] equals 4.8 × 10−5 mol L−1 at the first laser pulse.c The second radical of the initiator R0,II is considered to not chain initiate.d Only the plateau value is shown for ECR propagation reactivity, chain length dependency is considered based on the work of Heuts and Russell,71 see ESI S2.†e Chain length dependent apparent termination rates are considered (see ESI S2†);97 only the apparent unimer rate coefficient is shown, taking into account a correction factor 2;100 the fraction of termination done by recombination is assumed 0.9 for entries 11, 17 and 18, 0.3 for entries 12 and 19, and 0.1 for entry 13, in agreement with literature data;101,102 one of the disproportionation products is a macromonomer (not assumed reactive).f Assumed equal to kapp(t,e−e)(1,1).g Assumed equal to kapp(t,e−e) (1,l); kapp(t,e−e) (1,1) is reported here.h Assumed equal to kapp(t,e−m) (1,l); kapp(t,e−m) (1,l) is reported here.i Termination of the PMR against small radicals. Assumed equal to kapp(t,e−e) (1,l); kapp(t,p−p) (1,1) is reported here. | ||||||
| 1 | Photo-dissociationa,b |  |
18 and 28 | |||
| 2 | Chain initiationc | 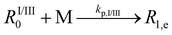 |
2.4 × 108 | 17.9 | 2.1 × 105 | 25, 34 and 95 |
| 3 | Propagationd |  |
2.2 × 107 | 17.9 | 1.9 × 104 | 25 |
| 4 |  |
1.94 × 106 | 28.3 | 1.4 × 101 | 18 | |
| 5 |  |
kp,P = γ(kp,e − kp,m) + kp,m | This work | |||
| 6 | Backbiting |  |
1.6 × 108 | 34.7 | 1.9 × 102 | 18 |
| 7 |  |
kbb,P = δkbb | This work | |||
| 8 | Chain transfer to monomer |  |
2.9 × 105 | 32.6 | 7.8 × 10−1 | 96 |
| 9 |  |
2.0 × 105 | 46.1 | 2.7 × 10−3 | 96 | |
| 10 |  |
2.9 × 105 | 32.6 | 7.8 × 10−1 | This work | |
| 11 | Terminatione |  |
1.3 × 1010 | 8.4 | 9.6 × 108 | 97 |
 |
||||||
| 12 |  |
4.2 × 109 | 6.6 | 2.1 × 108 | 97 | |
 |
||||||
| 13 |  |
9.0 × 106 | 5.6 | 2.0 × 106 | 97 | |
 |
||||||
| 14 | 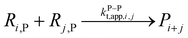 |
1.3 × 1010 | 8.4 | 9.6 × 108 | This work | |
 |
||||||
| 15 |  |
1.3 × 1010 | 8.4 | 9.6 × 108 | This work | |
 |
||||||
| 16 |  |
4.2 × 109 | 6.6 | 2.1 × 108 | This work | |
 |
||||||
| 17 |  |
1.3 × 1010 | 8.4 | 9.6 × 108 | f | |
| 18 |  |
1.3 × 1010 | 8.4 | 9.6 × 108 | g | |
| 19 |  |
4.2 × 109 | 6.6 | 2.1 × 108 | h | |
| 20 |  |
1.3 × 1010 | 8.4 | 9.6 × 108 | i | |
Specifically, the monomer conversion profile time range (hour scale) and the branching density (1–3%) are in line with typical experimental variations.106,107 Note that Zhang et al.108 e.g. shows that a methyl acrylate (MA) conversion of 40% results in roughly half an hour. As nBuA propagates faster than MA, the dark green line in Fig. 3a can be seen as at least qualitatively representative.
Moreover, Fig. 3 presents the updates for the conversion profile, log-MMD and branching density in case γ values highly different from 1 are considered (not green but red lines). It follows that for the lowest γ value of zero, a completely different FRP is simulated. If γ is (very) low, implying an MCR-like propagation behavior for PMR, we obtain a very strong retardation, a very pronounced lowering of the chain length (although the branching density remains the same). These shifts are very unlikely seeing that common experimental FRP ranges106,107 are closer to the green lines/points (γ values larger than 0.01).
Furthermore, as illustrated in Fig. S3 of the ESI,† PMR backbiting has no impact on the key FRP properties, even if a very unrealistic high rate coefficient would be employed, implying a very high backbiting scaling factor δ (eqn (3)).
DFT mechanistic insights: a γ value likely not too close to 1
The DFT predicted rate coefficients are shown in Table 2 along with a previously published result via computational chemistry.69 Our calculations reveal a higher activation energy and a lower pre-exponential parameter for PMR propagation, which could be related to the use of difference combination of basis set and model for the energetic correction. The difference between the literature published rate coefficient and our DFT calculation must be seen as qualitatively close. A comparison of exact numbers must be made with care because the energy correction method and the basis sets used are different, which can cause even orders of magnitude of difference. Moreover, the DFT predictions for ECR and MCR propagation are a good match with experimental values found out in literature.25,72| Reaction | Model/basis set | A, L mol−1 s−1 | Ea, kJ mol−1 | k (306 K), L mol−1 s−1 | Ref. |
|---|---|---|---|---|---|
| ECR propagation | B3LYP/M06-2X//6-311+G(d,p) | 7.21 × 106 | 21.3 | 1.7 × 103 | This work |
| MCR propagation | 8.93 × 105 | 25.0 | 4.9 × 101 | This work | |
| PMR propagation | 1.33 × 106 | 27.5 | 2.7 × 101 | This work | |
| B3LYP/MPWB1K//6-31G(d,p) | 1.17 × 105 | 20.2 | 4.2 × 101 | 69 |
According to the computational chemistry results, the calculated PMR propagation rate coefficient is lower than the ECR propagation rate coefficient and more similar to the rate coefficient of the MCR propagation, hence, γ is likely not too close to 1. The FRP results of Fig. 3 hinted at the opposite result so that overall intermediate γ values are too be expected. In any case, one should be careful by simply plugging in values from computational chemistry in kinetic modeling studies. However, the current DFT study gives credibility to the existence of a PMR with different reactivity than an MCR and ECR.
Further mechanistic insights: introducing a non-zero δ
The PMR species is likely capable of undergoing backbiting, similar to an ECR, although with some mechanistic differences. The ECR readily undergoes backbiting, due to the availability of a hydrogen atom for abstraction at a position that facilitates the formation of a stable 6-membered ring transition state. In contrast, the PMR has a more restricted polymer backbone, implying at first sight a δ lower than 1. However, as shown at the top of Fig. 4, a PMR has available hydrogens atoms on both sides (“left” and “right”) so that ignoring the previous effect a δ of 2 could be used.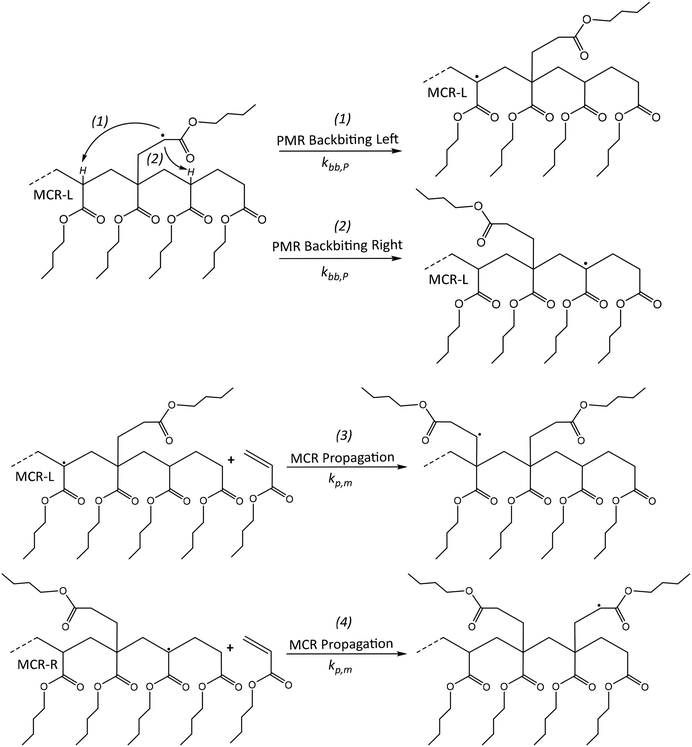 | ||
| Fig. 4 Top: Two backbiting reactions for PMR, for simplicity L(eft) and R(ight); Bottom: follow-up propagations. | ||
The most likely reaction at low temperature conditions for the formed MCRs is further propagation with monomer, leading to the structures depicted in Fig. 4 (bottom). The obtained products represent extra PMRs in terms of the radical placement in relation to the polymer backbone. However, now the structures have only one hydrogen atom available for an extra abstraction, as opposed to the two hydrogen atoms present in the initially formed PMR. This structural difference creates an issue with the previously introduced factor 2 used to account for the two backbiting possibilities (assuming a “lumped” PMR species). One can thus expect more a factor between 1 and 2 (still assuming similar mobilities between “left” and “right”).
Furthermore, the consideration of PMR backbiting (and further reactions) can result in a series of short branches next to each other. Such PMR-based mechanism increases the number of branches and additionally serves as a new mechanism for radical migration, similar to the consecutive six-ring hydrogen abstraction mechanism proposed by Kajiwara.89–91 This author stated that an actual mechanism is still ambiguous but there should be some stabilized mechanism to form helical structures of the model propagating radicals that have longer alkyl side groups. In this context, we hypothesize that the PMR will be part of the cause of said phenomena.
Note that short chain branching is a well-known structural property of vinyl polymers such as low density polyethylene.93 However, the consideration of PMR backbiting in acrylate polymerization kinetics (and further reactions) can result in two types of different branches: the first, a series of sequential short branches next to each other separated only by one monomeric unit, the second, a branch with 3 or more units with little 1 unit protrusions. The first is a product of the PMR backbiting towards the “right” (see Fig. 4) and then further propagation of the MCR/PMR. The second is a product of the PMR backbiting towards the “left” (see also Fig. 4), resulting in a 3 unit branch with a small 1 unit protrusion. This last type of branch can be further extended with further PMR backbiting/MCR propagation sequences, extending the short branch by one unit and adding one small protrusion each time the cycle is repeated.
Kinetic Monte Carlo PLP simulations to determine γ and δ
As highlighted in eqn (2), γ is a factor that adjusts the value of kp,P linearly between its extreme theoretical values of either MCR or ECR propagation behavior (γ = 0 and 1). In this subsection, we exploit PLP conditions to identify in the SEC trace sensitivities towards this γ factor. In a first phase, we deal with a frequency of 500 Hz, 100 laser pulses, a temperature of 306 K, and bulk conditions (δ fixed to 1).The results of the sensitivity analysis are shown in Fig. 5 (left) and indicate sensitivity of the PLP-SEC peak heights with respect to a γ variation. With γ becoming smaller, the average length of the polymer chains is reduced, because the PMR propagation resembles more the slower MCR propagation. This is consistent with the height of the first peak increasing (more shorter chains) and a reducing of the height of the second peak (less longer chains). The same trend is followed by the left and right tail of the MMD. The front (left tail), dealing with shorter chains, is more evident in case γ is lower, and the (right) tail, dealing with longer chains becomes less stretched in case γ is lower.
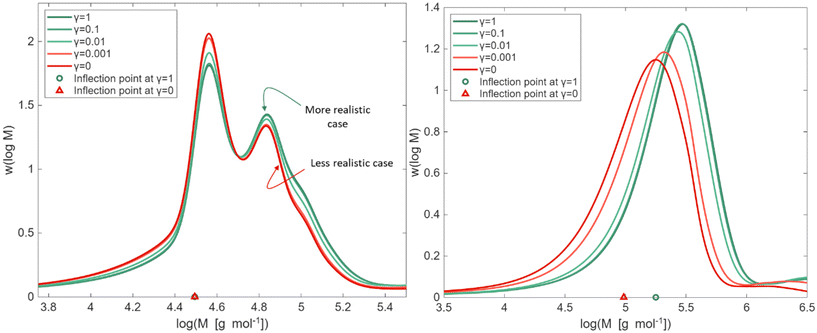 | ||
| Fig. 5 Left: kMC simulation of bulk PLP of nBuA at a laser pulse frequency of 500 Hz and 306 K, with a variation of γ (eqn (2); γ = 1 implying kp,P = kp,e and γ = 0 implying kp,P = kp,m). Right similar plot but at a lower laser pulse frequency of 50 Hz; on the x-axis the identification of the first inflection points (left coinciding; right shift). Same coloring as in Fig. 3, regarding expected behavior. | ||
It should be reminded that in Fig. 5 (left) the γ values between 1 and 0.01 are the more realistic ones. As shown in Fig. S4 of the ESI,† still at 500 Hz but taking a temperature of 325 K, a reasonable experimental description of the PLP log-MMD is indeed obtained for a γ of 0.1. It should although be reminded that no other parameters have been tuned and here only one literature frequency is considered.
Notably, as shown by the triangles in Fig. 5 (left), the γ variation at this studied high frequency of 500 Hz does not move the first inflection point of the MMD, which is used to determine kp,app via eqn (1). This implies the overall consistency of the PLP-SEC method previously applied to determine kp,app for acrylates.21–27 The introduction of PMR as a different species does thus not invalidate previous research using a “simplified” model under the conditions of high frequency and low temperature. Complementary, the PMR as a new species can help to describe other features of the log-MMD and branching levels that were previously inaccessible.
The extra PMR species changes the quasi-steady state based expression of the average propagation rate coefficient kp,av, as highlighted in section S5 of the ESI.† Such average kp,av is more representative for lower PLP frequencies, hence, one can expect that at such frequencies the consistency of the inflection points no longer holds. Indeed, as shown in Fig. 5 (right) at a lower frequency of 50 Hz, the inflection point of the MMD becomes sensitive to the value of γ. Lower values of γ shift the inflection point, due to the slower propagation with PMR, reducing kp,app even by half if γ is very low. However, the likelihood of such a low value of γ is very low, reminding the results in Fig. 3 for the FRP case.
The clear sensitivity of the peak heights at different frequencies in Fig. 6 (left) is the basis to experimentally determine kp,P in future work, at least if the frequencies are not too low (reminding Fig. 5; right). Fig. 6 (left) shows how the ratio of these peak heights (first vs. second: h1/h2) changes dependent on the pulse laser frequency as a function of γ. For a lower γ, the peak ratio increases and for a given γ a lower frequency has the same effect. For a lower γ (close to 0), a quasi-linear behavior is obtained with a lower frequency, and for a higher γ (close to 1) a clearer change in slope is obtained, with more steepness for a lower frequency. Extra sensitivity is thus identified, as slope dependency would be seen or not, likely the former seeing the discussion of the FRP data in Fig. 3.
 | ||
| Fig. 6 Left peak heights ratio at different values of γ (eqn (2)) for PLP of nBuA at a laser pulse frequency of 500 Hz, at 306 K, and in bulk. The green lines represent the more likely values of γ within the 1–0.01 range (see Fig. 1), and the red lines represent the more unlikely values of γ between 0.001–0. Right Corresponding branching densities. | ||
As shown in section S6 of the ESI,† at lower frequencies, the bimodality of the SEC trace starts to disappear, consistent with Nikitin's work on backbiting.43 The behavior of the double peaks is maintained roughly until a frequency of 300 Hz, with further lowering resulting in the loss of the bimodality behavior for γ values closer to 0.
It should also be admitted that the experimental determination of kp,P by using the peak heights comes with several challenges, because these heights are also dependent on the termination kinetics, the pulse radical production and SEC broadening. Regarding termination kinetics, section S1 of the ESI† shows the negligible relevance of PMR termination towards the overall system. The pulse radical production in turn can cause differences in the peak heights as the amount of radicals produced change the rates of termination, causing macromolecules to move from one peak to the other. However, the amount of initiator radicals produced per pulse can be calculated using the Beer–Lambert law:92 eqn (5). This equation allows to calculate the amount of radicals produced per pulse, and it is dependent on the properties of the laser and volume of the sample, which are not affected by the PMR kinetics. Additionally, the amount of radicals produced is affected by the quantum yield, which can also be related to the peak heights,28 although this parameter can be determined at a low temperature at which PMR/MCR are irrelevant. Hence, effectively decoupling the pulse radical production from the PMR kinetics is possible. Similarly, the band broadening function can be determined through independent experiments, especially for the acrylics esters whose propagation rates are high.109 These independent calibration experiments use narrow standard polymers, integrity plots, or band broadening function deconvolution with known distributions.110,111
Fig. S7 of the ESI† shows the fractions of ECR, MCR and PMR as a function of temperature for different γ values at a frequency of 20 Hz, supported by EPR experimental data from Willemse et al.56 considering only ECR and MCR fractions. In any case, the MCR radicals are dominant and PMR radicals are the least present in such a way that the trend from Willemse et al.56 remains. Again the current work is thus in line with previously established trends.
Additional to the peak heights ratios, the branching density, which is accessible by NMR, shows sensitivity to the value of γ, as shown in Fig. 6 (right). In case PMR propagation becomes slower (smaller γ), the backbiting with PMR is more prominent, generating more one-unit branches besides each other in the polymer backbone, therefore, increasing the amount of branches as the value of γ decreases. Reminding the FRP results, a too low γ is although not expected, as otherwise the simulated values for the branching density are too high compared to typical measured branching densities of PLP-made acrylate polymers.112 Hence, the results in Fig. 6 (right) highlight that the branching density could serve as a property to determine the value of γ together with the peak heights ratio, although NMR analysis is more tedious. In any case, γ values between 0.1 and 1 seem to be undistinguishable.
For the δ factor (eqn (3)), the sensitivity toward PLP parameters is much less. For example, as shown in Section S8 of the ESI† there is no sensitivity towards branching density, the inflection point nor the peak height, even at unlikely high δ values (γ fixed at 1). However, by increasing the PLP solvent fraction, we can exploit the relation between the monomolecular backbiting reaction and the bimolecular propagation reaction. Fig. 7 shows the effect of varying the solvent fraction for the branching density at different values of δ. It follows that for a sufficiently diluted system a certain sensitivity is obtained, at least in case δ would be above 1, which is unfortunately in the more unrealistic zone of expected parameters. Hence, we expect that in many experimental cases we would end up with a δ set to 1.
 | ||
| Fig. 7 Branching density as a function of the solvent fraction for different δ (eqn (3)) values; PLP conditions: 500 Hz, at 306 K, fixing the value of γ to 1. In practice, one likely will end up setting δ equal to 1. | ||
Roadmap to determine kp,e, kp,m, kp,P, kbb, kbb,P, and kβ.
Supported by previous work on kp,e and kβ determination18,25 and the insights in the present work, we can formulate a step-wise PLP roadmap to come to reliable kp,e, kp,m, kp,P, kbb, kbb,P, and kβ data, as illustrated in Fig. 8.
For the PLP experiments, a distinction is made between frequency and temperature as well as four steps, in each step e.g. accounting for 3 temperatures to enable for the determination of Arrhenius parameters.
The first step deals with high frequencies and a low temperature to only allow for sensitivity toward the kinetic parameter with the highest rate coefficient and link to the primary ECR. Hence, Step 1 is devoted to the determination of kp,e. In Step 2, the temperature is increased and the frequency lowered so that backbiting and tertiary propagation become kinetically relevant. Their joint estimation can be done to then check whether kp,P (or better said γ; eqn (2)) is interfering or not. Likely this is not the case (so more γ away from 0) as verifiable by looking at the peak height ratios for different frequencies in Step 3. In parallel, kbb,P (or δ; eqn (3)) can be assessed but it can be expected that this parameter needs to be approximated by kbb (δ = 1). In Step 4, the temperature can be increased to allow for β-scission and, hence, the determination of kβ is within reach.
Conclusions
By combining DFT and kMC simulations it is demonstrated that a MCR in nBuA radical polymerization is not directly transformed in a fully developed ECR. From a fundamental point of view, a propagated MCR (PMR) is better introduced to describe the kinetics in a more fundamental manner.This PMR is kinetically defined by a transition propagation factor γ somewhat between 0 and 1, these borders implying MCR and ECR propagation behavior, respectively. kMC simulations under FRP conditions reveal that γ is likely not close to 0, and DFT calculations that γ is likely not close to 1. More importantly, the ratio of the peak heights under PLP conditions (at sufficiently high frequencies) is sensitive to γ, so that this experimentally accessible parameter can become relevant for γ determination in case the interfering model parameters, e.g. quantum yield, have been determined at low temperatures. Current literature PLP data at 500 Hz suggest a γ value of 0.1 at 325 K.
Furthermore, it is shown that PMR species can backbite, leading to a new migration mechanism as well as the formation of consecutive branches. Practically, the associated backbiting scaling factor δ can be taken equal to 1, although it can be worthwhile to consider a variation of the solvent volume fraction in the PLP region.
The current work puts forward an updated roadmap for the determination of acrylate specific rate coefficients, differentiating between the determination of kp,e, kp,m, kp,P, kbb, kbb,P, and kβ.
Conflicts of interest
There are no conflicts to declare.Data availability
All key data is reported in the manuscript and the ESI.†Acknowledgements
Y. W. M. acknowledges FWO Flanders for a postdoctoral grant (12B3Y24N). L. Trossaert acknowledges FWO Flanders for a PhD fellowship grant (1S86924N).References
- N. Ballard and J. M. Asua, Radical polymerization of acrylic monomers: An overview, Prog. Polym. Sci., 2018, 79, 40–60 CrossRef CAS.
- E. Passaglia, et al., Some recent advances in polyolefin functionalization, Polym. Int., 2014, 63(1), 12–21 CrossRef CAS.
- P. Gloor, et al., Chemical modification of polyolefins by free radical mechanisms: a modelling and experimental study of simultaneous random scission, branching and crosslinking, Polymer, 1994, 35(5), 1012–1030 CrossRef CAS.
- H. Günaydin, et al., Modeling the free radical polymerization of acrylates, Int. J. Quantum Chem., 2005, 103(2), 176–189 CrossRef.
- A. N. Peck and R. A. Hutchinson, Secondary reactions in the high-temperature free radical polymerization of butyl acrylate, Macromolecules, 2004, 37(16), 5944–5951 CrossRef CAS.
- E. Guo, et al., A cocktail strategy for enhancing flame retardance and water resistance of butyl acrylate coatings, Mater. Chem. Phys., 2021, 263, 124367 CrossRef CAS.
- L. E. Elizalde, et al., Synthesis of butyl acrylate–styrene–TMI latexes and their application as water-based coatings, J. Coat. Technol. Res., 2020, 17, 911–919 CrossRef CAS.
- J. Wu, et al., Fabrication of water-resistance and durable antimicrobial adhesion polyurethane coating containing weakly amphiphilic poly (isobornyl acrylate) Side chains, Prog. Org. Coat., 2020, 147, 105812 CrossRef CAS.
- A. Navaruckiene, et al., Influence of Vanillin Acrylate-Based Resin Composition on Resin Photocuring Kinetics and Antimicrobial Properties of the Resulting Polymers, Materials, 2021, 14(3), 653 CrossRef CAS PubMed.
- M. Lebedevaite, V. Talacka and J. Ostrauskaite, High biorenewable content acrylate photocurable resins for DLP 3D printing, J. Appl. Polym. Sci., 2021, 138(16), 50233 CrossRef CAS.
- T. Pirman, et al., Free radical copolymerization kinetics of bio-based dibutyl itaconate and n-butyl acrylate, Chem. Eng. J., 2024, 499, 156127 CrossRef CAS.
- S. Rubio, et al., Tetrahydrofurfuryl methacrylate helps to produce biobased hydrophobic waterborne protective coatings by emulsion polymerization, Prog. Org. Coat., 2025, 203, 109159 CrossRef CAS.
- Y. W. Marien, et al., Exploiting the pulsed laser polymerization-size exclusion chromatography technique to retrieve kinetic parameters in radical polymerization: State-of-the-art and future challenges, Adv. Chem. Eng., 2020, 59–95 CAS.
- R. X. Willemse, et al., PLP− ESR Monitoring of Midchain Radicals in n-Butyl Acrylate Polymerization, Macromolecules, 2005, 38(12), 5098–5103 CrossRef CAS.
- J. Mätzig, et al., Kinetic Monte Carlo Simulations as a Tool for Unraveling the Impact of Solvent and Temperature on Polymer Topology for Self-Initiated Butyl Acrylate Radical Polymerizations at High Temperatures, Macromol. Theory Simul., 2023, 32(4), 2300007 CrossRef.
- A. N. Nikitin, et al., Effect of Intramolecular Transfer to Polymer on Stationary Free-Radical Polymerization of Alkyl Acrylates, 5 – Consideration of Solution Polymerization up to High Temperatures, Macromol. React. Eng., 2010, 4(11–12), 691–706 CrossRef CAS.
- M. Edeleva, et al., Impact of side reactions on molar mass distribution, unsaturation level and branching density in solution free radical polymerization of n-butyl acrylate under well-defined lab-scale reactor conditions, Polym. Chem., 2021, 12(14), 2095–2114 RSC.
- A. B. Vir, et al., From n-butyl acrylate Arrhenius parameters for backbiting and tertiary propagation to β-scission via stepwise pulsed laser polymerization, Polym. Chem., 2019, 10(30), 4116–4125 RSC.
- A. P. Aleksandrov, et al., Kinetics of laser-initiated polymerization and molecular-weight distribution of the resultant polymer, Sov. J. Quantum Electron., 1977, 7(5), 547 CrossRef.
- O. F. Olaj, I. Bitai and G. Gleixner, The laser flash-initiated polymerization as a tool of evaluating (individual) kinetic constants of free radical polymerization, 1. Outline of method and first results, Makromol. Chem., 1985, 186(12), 2569–2580 CrossRef CAS.
- M. Buback, et al., Critically evaluated rate coefficients for free-radical polymerization, 1. Propagation rate coefficient for styrene, Macromol. Chem. Phys., 1995, 196(10), 3267–3280 CrossRef CAS.
- S. Beuermann, et al., Critically evaluated rate coefficients for free-radical polymerization, 2. Propagation rate coefficients for methyl methacrylate, Macromol. Chem. Phys., 1997, 198(5), 1545–1560 CrossRef CAS.
- S. Beuermann, et al., Critically evaluated rate coefficients for free-radical polymerization, 3. Propagation rate coefficients for alkyl methacrylates, Macromol. Chem. Phys., 2000, 201(12), 1355–1364 CrossRef CAS.
- S. Beuermann, et al., Critically Evaluated Rate Coefficients for Free-Radical Polymerization, 4, Macromol. Chem. Phys., 2003, 204(10), 1338–1350 CrossRef CAS.
- J. M. Asua, et al., Critically Evaluated Rate Coefficients for Free-Radical Polymerization, 5, Macromol. Chem. Phys., 2004, 205(16), 2151–2160 CrossRef CAS.
- S. Beuermann, et al., Critically evaluated rate coefficients for free-radical polymerization Part 6: Propagation rate coefficient of methacrylic acid in aqueous solution (IUPAC Technical Report), Pure Appl. Chem., 2007, 79(8), 1463–1469 CrossRef CAS.
- C. Barner-Kowollik, et al., Critically evaluated rate coefficients in radical polymerization – 7. Secondary-radical propagation rate coefficients for methyl acrylate in the bulk, Polym. Chem., 2014, 5(1), 204–212 RSC.
- Y. W. Marien, et al., Estimating the photodissociation quantum yield from PLP-SEC peak heights, Polym. Chem., 2017, 8(20), 3124–3128 RSC.
- A. P. Haehnel, et al., Solvent Effects on Acrylate kp in Organic Media?—A Systematic PLP–SEC Study, Macromol. Rapid Commun., 2014, 35(23), 2029–2037 CrossRef CAS PubMed.
- C. Barner-Kowollik, F. Günzler and T. Junkers, Pushing the limit: Pulsed laser polymerization of n-butyl acrylate at 500 Hz, Macromolecules, 2008, 41(23), 8971–8973 CrossRef CAS.
- P. Drawe and M. Buback, The PLP–SEC Method: Perspectives and Limitations, Macromol. Theory Simul., 2016, 25(1), 74–84 CrossRef CAS.
- J. Sarnecki and J. Schweer, Conditions for the Determination of Precise and Accurate Free-Radical Propagation Rate Coefficients from Pulsed-Laser-Made Polymer, Macromolecules, 1995, 28(12), 4080–4088 CrossRef CAS.
- A. N. Nikitin, et al., Detection of PLP structure for accurate determination of propagation rate coefficients over an enhanced range of PLP-SEC conditions, Macromolecules, 2018, 52(1), 55–71 CrossRef.
- Y. W. Marien, et al., Kinetic Monte Carlo modeling extracts information on chain initiation and termination from complete PLP-SEC traces, Macromolecules, 2017, 50(4), 1371–1385 CrossRef CAS.
- G. B. Desmet, et al., Ab initio based kinetic Monte Carlo analysis to unravel the propagation kinetics in vinyl acetate pulsed laser polymerization, Polym. Chem., 2017, 8(46), 7143–7150 RSC.
- R. A. Hutchinson, M. T. Aronson and J. R. Richards, Analysis of pulsed-laser-generated molecular weight distributions for the determination of propagation rate coefficients, Macromolecules, 1993, 26(24), 6410–6415 CrossRef CAS.
- P. Castignolles, Transfer to Polymer and Long–Chain Branching in PLP–SEC of Acrylates, Macromol. Rapid Commun., 2009, 30(23), 1995–2001 CrossRef CAS PubMed.
- T. Junkers and C. Barner, Kowollik, The role of mid–chain radicals in acrylate free radical polymerization: Branching and scission., J. Polym. Sci., Part A: Polym. Chem., 2008, 46(23), 7585–7605 CrossRef CAS.
- C. Plessis, et al., Evidence of Branching in Poly (butyl acrylate) Produced in Pulsed–Laser Polymerization Experiments, Macromol. Rapid Commun., 2003, 24(2), 173–177 CrossRef CAS.
- C. Plessis, et al., A decrease in effective acrylate propagation rate constants caused by intramolecular chain transfer, Macromolecules, 2000, 33(1), 4–7 CrossRef CAS.
- A. N. Nikitin, et al., Determination of Propagation Rate Coefficient of Acrylates by Pulsed–Laser Polymerization in the Presence of Intramolecular Chain Transfer to Polymer, Macromol. Rapid Commun., 2003, 24(13), 778–782 CrossRef CAS.
- M. Buback, P. Hesse and I. Lacík, Propagation Rate Coefficient and Fraction of Mid–Chain Radicals for Acrylic Acid Polymerization in Aqueous Solution, Macromol. Rapid Commun., 2007, 28(21), 2049–2054 CrossRef CAS.
- A. N. Nikitin, et al., Determination of intramolecular chain transfer and midchain radical propagation rate coefficients for butyl acrylate by pulsed laser polymerization, Macromolecules, 2007, 40(24), 8631–8641 CrossRef CAS.
- M. L. Coote, et al., Copolymerization Propagation Kinetics of Styrene and Methyl Methacrylate Revisited. 1. Pulsed Laser Polymerization Study, Macromolecules, 1997, 30(26), 8182–8190 CrossRef CAS.
- R. A. Hutchinson, et al., A pulsed-laser study of penultimate copolymerization propagation kinetics for methyl methacrylate/n-butyl acrylate, Ind. Eng. Chem. Res., 1997, 36(4), 1103–1113 CrossRef CAS.
- Y. W. Marien, et al., Translating Simulated Chain Length and Molar Mass Distributions in Chain-Growth Polymerization for Experimental Comparison and Mechanistic Insight, Macromol. Theory Simul., 2021, 30(3), 2170005 CrossRef.
- K. De Smit, et al., Roadmap for Monomer Conversion and Chain Length-Dependent Termination Reactivity Algorithms in Kinetic Monte Carlo Modeling of Bulk Radical Polymerization, Ind. Eng. Chem. Res., 2020, 59(52), 22422–22439 CrossRef CAS.
- T. Junkers and C. Barner-Kowollik, Optimum Reaction Conditions for the Synthesis of Macromonomers Via the High-Temperature Polymerization of Acrylates, Macromol. Theory Simul., 2009, 18(7–8), 421–433 CrossRef CAS.
- M. Drache, et al., Identification of β scission products from free radical polymerizations of butyl acrylate at high temperature, Polym. Chem., 2019, 10(15), 1956–1967 RSC.
- R. X. E. Willemse and A. M. van Herk, Determination of Propagation Rate Coefficients of a Family of Acrylates with PLP-MALDI-ToF-MS, Macromol. Chem. Phys., 2010, 211(5), 539–545 CrossRef CAS.
- B. Wenn and T. Junkers, Kilohertz Pulsed-Laser-Polymerization: Simultaneous Determination of Backbiting, Secondary, and Tertiary Radical Propagation Rate Coefficients for tert-Butyl Acrylate, Macromol. Rapid Commun., 2016, 37(9), 781–787 CrossRef CAS PubMed.
- B. Wenn and T. Junkers, Kilohertz Pulsed–Laser–Polymerization: Simultaneous Determination of Backbiting, Secondary, and Tertiary Radical Propagation Rate Coefficients for tert–Butyl Acrylate, Macromol. Rapid Commun., 2016, 37(9), 781–787 CrossRef CAS PubMed.
- G. Quintens and T. Junkers, Pulsed laser polymerization–size exclusion chromatography investigations into backbiting in ethylhexyl acrylate polymerization, Polym. Chem., 2022, 13(14), 2019–2025 RSC.
- Y. W. Marien, et al., An alternative method to estimate the bulk backbiting rate coefficient in acrylate radical polymerization, Polym. Chem., 2016, 7(42), 6521–6528 RSC.
- J. Barth, et al., EPR Analysis of n-Butyl Acrylate Radical Polymerization, Macromol. Rapid Commun., 2009, 30(23), 1969–1974 CrossRef CAS PubMed.
- R. X. E. Willemse, et al., PLP−ESR Monitoring of Midchain Radicals in n-Butyl Acrylate Polymerization, Macromolecules, 2005, 38(12), 5098–5103 CrossRef CAS.
- J. Barth and M. Buback, SP–PLP–EPR—A Novel Method for Detailed Studies into the Termination Kinetics of Radical Polymerization, Macromol. React. Eng., 2010, 4(5), 288–301 CrossRef CAS.
- H. Kattner, P. Drawe and M. Buback, Novel access to propagation rate coefficients of radical polymerization by the SP–PLP–EPR method, Macromol. Chem. Phys., 2015, 216(16), 1737–1745 CrossRef CAS.
- H. Kattner and M. Buback, Propagation and chain-length-dependent termination rate coefficients deduced from a single SP–PLP–EPR experiment, Macromolecules, 2016, 49(10), 3716–3722 CrossRef CAS.
- J. Barth, Radical polymerization kinetics in systems with transfer reactions studied by pulsed-laser-polymerization and online EPR-detection, 2011 Search PubMed.
- M. Buback, et al., Free–Radical Termination Kinetics Studied Using a Novel SP–PLP–ESR Technique, Macromol. Rapid Commun., 2004, 25(10), 1004–1009 CrossRef CAS.
- H. Kattner and M. Buback, Chain-length-dependent termination of styrene bulk homopolymerization studied by SP− PLP− EPR, Macromolecules, 2015, 48(2), 309–315 CrossRef CAS.
- J. Barth and M. Buback, SP–PLP–EPR Investigations into the Chain–Length–Dependent Termination of Methyl Methacrylate Bulk Polymerization, Macromol. Rapid Commun., 2009, 30(21), 1805–1811 CrossRef CAS PubMed.
- H. Kattner and M. Buback., Detailed Investigations into Radical Polymerization Kinetics by Highly Time–R esolved SP–PLP–EPR. in Macromolecular Symposia, Wiley Online Library, 2013 Search PubMed.
- J. Barth, et al., Chain–Length–Dependent Termination in Radical Polymerization of Acrylates, Macromol. Chem. Phys., 2011, 212(13), 1366–1378 CrossRef CAS.
- J. Barth and M. Buback, SP-PLP-EPR Study into the termination kinetics of methacrylic acid radical polymerization in aqueous solution, Macromolecules, 2011, 44(6), 1292–1297 CrossRef CAS.
- J. Barth, W. Meiser and M. Buback, SP-PLP-EPR study into termination and transfer kinetics of non-ionized acrylic acid polymerized in aqueous solution, Macromolecules, 2012, 45(3), 1339–1345 CrossRef CAS.
- N. Soerensen, et al., SP-PLP-EPR measurement of ATRP deactivation rate, Macromolecules, 2012, 45(9), 3797–3801 CrossRef CAS.
- D. Cuccato, et al., A Density Functional Theory Study of Secondary Reactions in n–Butyl Acrylate Free Radical Polymerization, Macromol. Theory Simul., 2013, 22(2), 127–135 CrossRef CAS.
- C. Y. Lin, et al., Ab Initio Study of the Penultimate Effect for the ATRP Activation Step Using Propylene, Methyl Acrylate, and Methyl Methacrylate Monomers, Macromolecules, 2007, 40(16), 5985–5994 CrossRef CAS.
- J. P. A. Heuts and G. T. Russell, The nature of the chain-length dependence of the propagation rate coefficient and its effect on the kinetics of free-radical polymerization. 1. Small-molecule studies, Eur. Polym. J., 2006, 42(1), 3–20 CrossRef CAS.
- F. A. Lugo, et al., Secondary reactions during acrylate radical polymerization: Determining their rate coefficients, Polymer, 2024, 300, 126938 CrossRef CAS.
- F. Serse, M. Salvalaglio and M. Pelucchi, First Principles Assessment of Solvent Induced Cage Effects on Intramolecular Hydrogen Transfer in the Free Radical Polymerization of Acrylates, Physical Chemistry Chemical Physics, 2024 Search PubMed.
- F. A. Lugo, et al., Improved Approach for ab Initio Calculations of Rate Coefficients for Secondary Reactions in Acrylate Free-Radical Polymerization, Polymers, 2024, 16(7), 872 CrossRef CAS PubMed.
- X. Yu and L. J. Broadbelt, Kinetic Study of 1,5-Hydrogen Transfer Reactions of Methyl Acrylate and Butyl Acrylate Using Quantum Chemistry, Macromol. Theory Simul., 2012, 21(7), 461–469 CrossRef CAS.
- S. Liu, et al., Backbiting and β-scission reactions in free-radical polymerization of methyl acrylate, Int. J. Quantum Chem., 2014, 114(5), 345–360 CrossRef CAS.
- N. Moghadam, et al., Theoretical Study of Intermolecular Chain Transfer to Polymer Reactions of Alkyl Acrylates, Ind. Eng. Chem. Res., 2015, 54(16), 4148–4165 CrossRef CAS.
- E. Mavroudakis, D. Cuccato and D. Moscatelli, Quantum Mechanical Investigation on Bimolecular Hydrogen Abstractions in Butyl Acrylate-Based Free Radical Polymerization Processes, J. Phys. Chem. A, 2014, 118(10), 1799–1806 CrossRef CAS PubMed.
- D. Cuccato, E. Mavroudakis and D. Moscatelli, Quantum Chemistry Investigation of Secondary Reaction Kinetics in Acrylate-Based Copolymers, J. Phys. Chem. A, 2013, 117(21), 4358–4366 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- D. A. McQuarrie and J. D. Simon, Physical chemistry: a molecular approach, University Science Books, Sausalito, CA, 1997, vol. 1 Search PubMed.
- A. Klamt, Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena, J. Phys. Chem., 1995, 99(7), 2224–2235 CrossRef CAS.
- A. Klamt, et al., Refinement and parametrization of COSMO-RS, J. Phys. Chem. A, 1998, 102(26), 5074–5085 CrossRef CAS.
- F. Eckert and A. Klamt, Fast solvent screening via quantum chemistry: COSMO–RS approach, AIChE J., 2002, 48(2), 369–385 CrossRef CAS.
- COSMOtherm, “COSMOlogic GmbH & Co. KG, a Dassault Systèmes Company”, 2019.
- M. Edeleva, et al., Connecting Gas-Phase Computational Chemistry to Condensed Phase Kinetic Modeling: The State-of-the-Art, Polymers, 2021, 13(18), 3027 CrossRef CAS PubMed.
- H. Eyring, The Activated Complex in Chemical Reactions, J. Chem. Phys., 1935, 3(2), 107–115 CrossRef CAS.
- C. Eckart, The penetration of a potential barrier by electrons, Phys. Rev., 1930, 35(11), 1303 CrossRef CAS.
- A. Kajiwara, Studying the Fundamentals of Radical Polymerization Using ESR in Combination with Controlled Radical Polymerization Methods, in Radical Polymerization, 2007, pp. 50–59 Search PubMed.
- A. Kajiwara, Electron Spin Resonance (ESR) Observation of Radical Migration Reactions in the Polymerization of Alkyl Acrylates, in Controlled/Living Radical Polymerization: Progress in ATRP, American Chemical Society, 2009, pp. 49–59 Search PubMed.
- A. Kajiwara, A combination of Electron Spin Resonance spectroscopy/atom transfer radical polymerization (ESR/ATRP) techniques for fundamental investigation of radical polymerizations of (meth)acrylates, Polymer, 2015, 72, 253–263 CrossRef CAS.
- R. W. Ricci, M. Ditzler and L. P. Nestor, Discovering the Beer-Lambert Law, J. Chem. Educ., 1994, 71(11), 983 CrossRef CAS.
- G. Odian, Principles of Polymerization, Wiley, 2004 Search PubMed.
- P. Castignolles, et al., Pulsed Laser Polymerization of Alkyl Acrylates: Potential Effects of the Oxygen Presence and High Laser Power, Macromol. Chem. Phys., 2006, 207(1), 81–89 CrossRef CAS.
- J. J. Haven, et al., Efficiency assessment of single unit monomer insertion reactions for monomer sequence control: kinetic simulations and experimental observations, Polym. Chem., 2015, 6(31), 5752–5765 RSC.
- S. Maeder and R. G. Gilbert, Measurement of Transfer Constant for Butyl Acrylate Free-Radical Polymerization, Macromolecules, 1998, 31(14), 4410–4418 CrossRef CAS.
- J. Barth, et al., Termination and Transfer Kinetics of Butyl Acrylate Radical Polymerization Studied via SP-PLP-EPR, Macromolecules, 2010, 43(9), 4023–4031 CrossRef CAS.
- F. M. Lewis and M. S. Matheson, Decomposition of Aliphatic Azo Compounds, J. Am. Chem. Soc., 1949, 71(2), 747–748 CrossRef CAS.
- R. Walz, B. Bömer and W. Heitz, Monomeric and polymeric azoinitiators, Makromol. Chem., 1977, 178(9), 2527–2534 CrossRef CAS.
- P. Derboven, et al., The Long and the Short of Radical Polymerization, Macromolecules, 2015, 48(3), 492–501 CrossRef CAS.
- A. K. Tripathi, J. G. Tsavalas and D. C. Sundberg, Monte Carlo Simulations of Free Radical Polymerizations with Divinyl Cross-Linker: Pre- and Postgel Simulations of Reaction Kinetics and Molecular Structure, Macromolecules, 2015, 48(1), 184–197 CrossRef CAS.
- S. Hamzehlou, et al., Analyzing the discrepancies in the activation energies of the backbiting and β-scission reactions in the radical polymerization of n-butyl acrylate, Polym. Chem., 2016, 7(11), 2069–2077 RSC.
- M. Buback, M. Busch and R. A. Lämmel, Modeling of molecular weight distribution in pulsed laser free–radical homopolymerizations, Macromol. Theory Simul., 1996, 5(5), 845–861 CrossRef CAS.
- A. D. Trigilio, et al., A Signal-To-Noise-Ratio-Based Automated Algorithm to accelerate Kinetic Monte Carlo Convergence in Basic Polymerizations, Adv. Theory Simul., 2024, 7(2), 2300637 CrossRef CAS.
- A. D. Trigilio, et al., Toward an Automated Convergence Tool for Kinetic Monte Carlo Simulation of Conversion, Distributions, and Their Averages in Non-dispersed Phase Linear Chain-Growth Polymerization, Ind. Eng. Chem. Res., 2023, 62(6), 2583–2593 CrossRef CAS.
- N. M. Ahmad, F. Heatley and P. A. Lovell, Chain Transfer to Polymer in Free-Radical Solution Polymerization of n-Butyl Acrylate Studied by NMR Spectroscopy, Macromolecules, 1998, 31(9), 2822–2827 CrossRef CAS.
- N. M. Ahmad, et al., Chain Transfer to Polymer and Branching in Controlled Radical Polymerizations of n-Butyl Acrylate, Macromol. Rapid Commun., 2009, 30(23), 2002–2021 CrossRef CAS PubMed.
- Z. Zhang, et al., Free radical polymerization of acrylates bearing acetylene for preparation of clickable polymers, Polymer, 2021, 228, 123906 CrossRef CAS.
- M. Buback, M. Busch and R. A. Lämmel, Modeling of molecular weight distribution in pulsed laser free-radical homopolymerizations, Macromol. Theory Simul., 1996, 5(5), 845–861 CrossRef CAS.
- G. Meira, M. Netopilík, M. Potschka, I. Schnöll-Bitai and J. Vega, Band Broadening Function in Size Exclusion Chromatography of Polymers: Review of Some Recent Developments, Macromol. Symp., 2007, 258, 186–197 CrossRef CAS.
- A. Goyon, D. Guillarme and S. Fekete, The importance of system band broadening in modern size exclusion chromatography, J. Pharm. Biomed. Anal., 2017, 135, 50–60 CrossRef CAS PubMed.
- G. Arzamendi and J. R. Leiza, Molecular Weight Distribution (Soluble and Insoluble Fraction) in Emulsion Polymerization of Acrylate Monomers by Monte Carlo Simulations, Ind. Eng. Chem. Res., 2008, 47(16), 5934–5947 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5py00343a |
| This journal is © The Royal Society of Chemistry 2025 |