The temperature dependence of the solution equilibrium constants for [(tBu)2Al(OPh)]2(μ-4,4′-bipy)
(1a), [(tBu)2Al(OPh)]2(μ-bipetha)
(2a, bipetha = 1,2-bis(4-pyridyl)ethane), and [(tBu)2Al(OPh)]2(μ-bipethe)
(3a, bipethe =
trans-1,2-bis(4-pyridyl)ethylene) in C6D6 and CDCl3 allow for the determination of ΔH and ΔS for the dissociation of one Al(tBu)2OPh moiety from the bridging ligand, i.e., 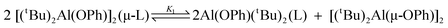 . For compounds 2a and 3a the ΔH values in C6D6
[99(2) kJ mol−1
(2a) and 109(5) kJ mol−1
(3a)] and CDCl3
[115(5) kJ mol−1
(2a) and 139(7) kJ mol−1
(3a)] were found to be inversely proportional with the dielectric constant of the solvent. In contrast, the ΔH value for 1a in CDCl3 is surprisingly small [14.9(7) kJ mol−1] and does not fit with the trends adopted by the bipetha and bipethe derivatives or the value obtained in C6D6
[110(2) kJ mol−1]. Unlike the other compounds and the C6D6 solutions, the CDCl3 solution of 1a allows for the observation of a second equilibrium
. For compounds 2a and 3a the ΔH values in C6D6
[99(2) kJ mol−1
(2a) and 109(5) kJ mol−1
(3a)] and CDCl3
[115(5) kJ mol−1
(2a) and 139(7) kJ mol−1
(3a)] were found to be inversely proportional with the dielectric constant of the solvent. In contrast, the ΔH value for 1a in CDCl3 is surprisingly small [14.9(7) kJ mol−1] and does not fit with the trends adopted by the bipetha and bipethe derivatives or the value obtained in C6D6
[110(2) kJ mol−1]. Unlike the other compounds and the C6D6 solutions, the CDCl3 solution of 1a allows for the observation of a second equilibrium 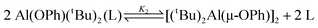 , for which the ΔH has been determined [4.5(3) kJ mol−1]. This result suggests that in CDCl3 bonding of the second Al(tBu)2OPh moiety to Al(OPh)(tBu)2(4,4′-bipy)
(1b) is stabilized by the presence of the first aluminium, which is counter to ab initio calculations that predicts the aluminium in Al(OPh)(tBu)2(L) should destabilize the Al–N interaction with a second Al(tBu)2OPh group. The BDE for dissociation of both Al(tBu)2OPh moieties from 1a–3a, and the energy of formation of hydrogen bond interactions with CHCl3, has been calculated by ab initio methods, and no unusual effects are inherent in 1a.
, for which the ΔH has been determined [4.5(3) kJ mol−1]. This result suggests that in CDCl3 bonding of the second Al(tBu)2OPh moiety to Al(OPh)(tBu)2(4,4′-bipy)
(1b) is stabilized by the presence of the first aluminium, which is counter to ab initio calculations that predicts the aluminium in Al(OPh)(tBu)2(L) should destabilize the Al–N interaction with a second Al(tBu)2OPh group. The BDE for dissociation of both Al(tBu)2OPh moieties from 1a–3a, and the energy of formation of hydrogen bond interactions with CHCl3, has been calculated by ab initio methods, and no unusual effects are inherent in 1a.
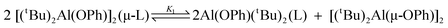 . For compounds 2a and 3a the ΔH values in C6D6
[99(2) kJ mol−1
(2a) and 109(5) kJ mol−1
(3a)] and
. For compounds 2a and 3a the ΔH values in C6D6
[99(2) kJ mol−1
(2a) and 109(5) kJ mol−1
(3a)] and 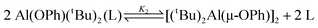 , for which the ΔH has been determined [4.5(3) kJ mol−1]. This result suggests that in
, for which the ΔH has been determined [4.5(3) kJ mol−1]. This result suggests that in ![Graphical abstract: Effects of solvent on the relative stability of mono and di-aluminium aryloxide complexes of bipyridines: anomalous behavior of [(tBu)2Al(OPh)]2(μ-4,4-bipy)](/en/Image/Get?imageInfo.ImageType=GA&imageInfo.ImageIdentifier.ManuscriptID=B501044F&imageInfo.ImageIdentifier.Year=2005)

 Please wait while we load your content...
Please wait while we load your content...