Scaled Brownian motion: a paradoxical process with a time dependent diffusivity for the description of anomalous diffusion

Abstract

Anomalous diffusion is frequently described by scaled Brownian motion (SBM), a Gaussian process with a power-law time dependent diffusion coefficient. Its mean squared displacement is 〈x²(t)〉 ≃ 2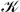(t)t with 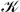(t) ≃ t^α−1 for 0 < α < 2. SBM may provide a seemingly adequate description in the case of unbounded diffusion, for which its probability density function coincides with that of fractional Brownian motion. Here we show that free SBM is weakly non-ergodic but does not exhibit a significant amplitude scatter of the time averaged mean squared displacement. More severely, we demonstrate that under confinement, the dynamics encoded by SBM is fundamentally different from both fractional Brownian motion and continuous time random walks. SBM is highly non-stationary and cannot provide a physical description for particles in a thermalised stationary system. Our findings have direct impact on the modelling of single particle tracking experiments, in particular, under confinement inside cellular compartments or when optical tweezers tracking methods are used.