Dynamical conductivity of gated AA-stacking multilayer graphene with spin–orbital coupling
Abstract
An efficient method, without the numerical diagonalization of a huge Hamiltonian matrix and calculation of a tedious Green’s function, is proposed to calculate the exact energy spectrum and dynamical conductivity in gated AA-stacking N-layer graphene (AANLG) with intrinsic spin–orbital coupling (SOC). The 2N × 2N tight-binding Hamiltonian matrix, velocity operator and Green’s function representation of AANLG are simultaneously reduced to N 2 × 2 diagonal block matrices through a proper transformation matrix. Gated AANLG with intrinsic SOC is reduced to N graphene-like layers. The energy spectrum of a graphene-like layer is E = ε⊥ ± ε∥, and ε⊥ depends on the interlayer interaction, gated voltage and layer number.  , where EMG is the energy spectrum of a graphene monolayer and Δ is the magnitude of the intrinsic SOC. More importantly, by inserting the diagonal block velocity operator and Green’s function representation in the Kubo formula, the exact dynamical conductivity of AANLG is shown to be
, where EMG is the energy spectrum of a graphene monolayer and Δ is the magnitude of the intrinsic SOC. More importantly, by inserting the diagonal block velocity operator and Green’s function representation in the Kubo formula, the exact dynamical conductivity of AANLG is shown to be 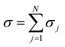 , the sum of the dynamical conductivity of N graphene-like layers. The analytical form of σj is presented and the dependence of σj on ε⊥, Δ, and chemical potential is clearly demonstrated. Moreover, the effect of the Rashba SOC on the electronic properties of AANLG is explored with the exact energy spectrum presented.
, the sum of the dynamical conductivity of N graphene-like layers. The analytical form of σj is presented and the dependence of σj on ε⊥, Δ, and chemical potential is clearly demonstrated. Moreover, the effect of the Rashba SOC on the electronic properties of AANLG is explored with the exact energy spectrum presented.


 Please wait while we load your content...
Please wait while we load your content...