Slow and long-ranged dynamical heterogeneities in dissipative fluids

Abstract

A two-dimensional bidisperse granular fluid is shown to exhibit pronounced long-ranged dynamical heterogeneities as dynamical arrest is approached. Here we focus on the most direct approach to study these heterogeneities: we identify clusters of slow particles and determine their size, N_c, and their radius of gyration, R_G. We show that 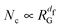, providing direct evidence that the most immobile particles arrange in fractal objects with a fractal dimension, d_f, that is observed to increase with packing fraction ϕ. The cluster size distribution obeys scaling, approaching an algebraic decay in the limit of structural arrest, i.e., ϕ → ϕ_c. Alternatively, dynamical heterogeneities are analyzed via the four-point structure factor S₄(q,t) and the dynamical susceptibility χ₄(t). S₄(q,t) is shown to obey scaling in the full range of packing fractions, 0.6 ≤ ϕ ≤ 0.805, and to become increasingly long-ranged as ϕ → ϕ_c. Finite size scaling of χ₄(t) provides a consistency check for the previously analyzed divergences of χ₄(t) ∝ (ϕ − ϕ_c)^−γ_χ and the correlation length ξ ∝ (ϕ − ϕ_c)^−γ_ξ. We check the robustness of our results with respect to our definition of mobility. The divergences and the scaling for ϕ → ϕ_c suggest a non-equilibrium glass transition which seems qualitatively independent of the coefficient of restitution.