Marginally compact hyperbranched polymer trees
Abstract
Assuming Gaussian chain statistics along the chain contour, we generate by means of a proper fractal generator hyperbranched polymer trees which are marginally compact. Static and dynamical properties, such as the radial intrachain pair density distribution ρpair(r) or the shear-stress relaxation modulus G(t), are investigated theoretically and by means of computer simulations. We emphasize that albeit the self-contact density 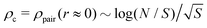 diverges logarithmically with the total mass N, this effect becomes rapidly irrelevant with increasing spacer length S. In addition to this it is seen that the standard Rouse analysis must necessarily become inappropriate for compact objects for which the relaxation time τp of mode p must scale as τp ∼ (N/p)5/3 rather than the usual square power law for linear chains.
diverges logarithmically with the total mass N, this effect becomes rapidly irrelevant with increasing spacer length S. In addition to this it is seen that the standard Rouse analysis must necessarily become inappropriate for compact objects for which the relaxation time τp of mode p must scale as τp ∼ (N/p)5/3 rather than the usual square power law for linear chains.



 Please wait while we load your content...
Please wait while we load your content...