Inertio-capillary cross-streamline drift of droplets in Poiseuille flow using dissipative particle dynamics simulations
Abstract
We find using dissipative particle dynamics (DPD) simulations that a deformable droplet sheared in a narrow microchannel migrates to steady-state position that depends upon the dimensionless particle capillary number 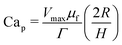 , which controls the droplet deformability (with Vmax the centerline velocity, μf the fluid viscosity, Γ the surface tension, R the droplet radius, and H the gap), the droplet (particle) Reynolds number
, which controls the droplet deformability (with Vmax the centerline velocity, μf the fluid viscosity, Γ the surface tension, R the droplet radius, and H the gap), the droplet (particle) Reynolds number 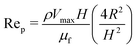 , which controls inertia, where ρ is the fluid density, as well as on the viscosity ratio of the droplet to the suspending fluid κ = μd/μf. We find that when the Ohnesorge number
, which controls inertia, where ρ is the fluid density, as well as on the viscosity ratio of the droplet to the suspending fluid κ = μd/μf. We find that when the Ohnesorge number 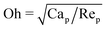 is around 0.06, so that inertia is stronger than capillarity, at small capillary number Cap < 0.1, the droplet migrates to a position close to that observed for hard spheres by Segre and Silberberg, around 60% of the distance from the centerline to the wall, while for increasing Cap the droplet steady-state position moves smoothly towards the centerline, reaching around 20% of the distance from centerline to the wall when Cap reaches 0.5 or so. For higher Oh, the droplet position is much less sensitive to Cap, and remains at around 30% of the distance from centerline to the wall over the whole accessible range of Cap. The results are insensitive to viscosity ratios from unity to the highest value studied here, around 13, and the drift towards the centerline for increasing Cap is observed for ratios of droplet diameter to gap size ranging from 0.1 to 0.3. We also find consistency between our predictions and existing perturbation theory for small droplet or particle size, as well as with experimental data. Additionally, we assess the accuracy of the DPD method and conclude that with current computer resources and methods DPD is not readily able to predict cross-stream-line drift for small particle Reynolds number (much less than unity), or for droplets that are less than one tenth the gap size, owing to excessive noise and inadequate numbers of DPD particles per droplet.
is around 0.06, so that inertia is stronger than capillarity, at small capillary number Cap < 0.1, the droplet migrates to a position close to that observed for hard spheres by Segre and Silberberg, around 60% of the distance from the centerline to the wall, while for increasing Cap the droplet steady-state position moves smoothly towards the centerline, reaching around 20% of the distance from centerline to the wall when Cap reaches 0.5 or so. For higher Oh, the droplet position is much less sensitive to Cap, and remains at around 30% of the distance from centerline to the wall over the whole accessible range of Cap. The results are insensitive to viscosity ratios from unity to the highest value studied here, around 13, and the drift towards the centerline for increasing Cap is observed for ratios of droplet diameter to gap size ranging from 0.1 to 0.3. We also find consistency between our predictions and existing perturbation theory for small droplet or particle size, as well as with experimental data. Additionally, we assess the accuracy of the DPD method and conclude that with current computer resources and methods DPD is not readily able to predict cross-stream-line drift for small particle Reynolds number (much less than unity), or for droplets that are less than one tenth the gap size, owing to excessive noise and inadequate numbers of DPD particles per droplet.



 Please wait while we load your content...
Please wait while we load your content...