Relative stability of FeS2 polymorphs with the random phase approximation approach

Abstract

Iron disulfide (FeS₂) has attracted a lot of interest for photovoltaic and photoelectrochemical applications due to its favorable electronic and optical properties. The theoretical description of FeS₂ has been confronted with the problem of common density functional approximations failing to correctly account for the relative stability of pyrite and marcasite polymorphs of FeS₂. We address this issue by using the adiabatic-connection fluctuation-dissipation theorem (ACFDT) in the random phase approximation (RPA). The relative stability of the two polymorphs is correctly predicted, and a significantly improved agreement with experiment compared to that from local, semi-local and hybrid functionals is obtained in terms of the enthalpy of transformation, regardless of the density functional approximations used in producing the input wave functions for RPA calculations. We attribute the stability of the pyrite phase to the electron correlation related to the low energy excitation from Fe d states to the S–S 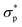state. Equilibrium volumes very close to the experimental values are predicted for both phases as well. The contributions of zero-point energy corrections and finite temperature effects are considered and found to be insignificant compared to dynamical correlation included in the ACFDT-RPA approach. This study highlights the importance of considering the difference in high-order dynamical correlation as described by ACFDT-RPA due to the distinction in the Kohn–Sham band structure for a correct description of the relative stability of competing phases that are energetically very close to each other.