The role of deformability in determining the structural and mechanical properties of bubbles and emulsions
Abstract
We perform computational studies of jammed particle packings in two dimensions undergoing isotropic compression using the well-characterized soft particle (SP) model and deformable particle (DP) model that we developed for bubbles and emulsions. In the SP model, circular particles are allowed to overlap, generating purely repulsive forces. In the DP model, particles minimize their perimeter, while deforming at fixed area to avoid overlap during compression. We compare the structural and mechanical properties of jammed packings generated using the SP and DP models as a function of the packing fraction ρ, instead of the reduced number density ϕ. We show that near jamming onset the excess contact number Δz = z − zJ and shear modulus 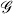 scale as Δρ0.5 in the large system limit for both models, where Δρ = ρ − ρJ and zJ ≈ 4 and ρJ ≈ 0.842 are the values at jamming onset. Δz and
scale as Δρ0.5 in the large system limit for both models, where Δρ = ρ − ρJ and zJ ≈ 4 and ρJ ≈ 0.842 are the values at jamming onset. Δz and 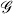 for the SP and DP models begin to differ for ρ ≳ 0.88. In this regime, Δz ∼
for the SP and DP models begin to differ for ρ ≳ 0.88. In this regime, Δz ∼ 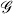 can be described by a sum of two power-laws in Δρ, i.e. Δz ∼
can be described by a sum of two power-laws in Δρ, i.e. Δz ∼ 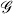 ∼ C0Δρ0.5 + C1Δρ1.0 to lowest order. We show that the ratio C1/C0 is much larger for the DP model compared to that for the SP model. We also characterize the void space in jammed packings as a function of ρ. We find that the DP model can describe the formation of Plateau borders as ρ → 1. We further show that the results for z and the shape factor
∼ C0Δρ0.5 + C1Δρ1.0 to lowest order. We show that the ratio C1/C0 is much larger for the DP model compared to that for the SP model. We also characterize the void space in jammed packings as a function of ρ. We find that the DP model can describe the formation of Plateau borders as ρ → 1. We further show that the results for z and the shape factor 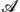 versus ρ for the DP model agree with recent experimental studies of foams and emulsions.
versus ρ for the DP model agree with recent experimental studies of foams and emulsions.



 Please wait while we load your content...
Please wait while we load your content...
