Full consideration of acoustic phonon scatterings in two-dimensional Dirac materials

Abstract

The in-plane acoustic phonon scattering in graphene is solved by considering fully inelastic acoustic phonon scatterings in two-dimensional (2D) Dirac materials for a large range of temperatures (T) and chemical potentials (μ). Rigorous analytical solutions and symmetry properties of Fermionic and Bosonic functions are obtained. We illustrate how doping alters the temperature dependence of acoustic phonon scattering rates. It is shown that the quasi-elastic and ansatz equations previously derived for acoustic phonon scatterings in graphene are limiting cases of the inelastic-scattering equations derived here. For heavily-doped graphene, we found that the high-T behavior of resistivity is better described by ρ(T,μ) ∝ T(1 − ζ_aμ²/3(k_BT)²) rather than a linear T behavior, and in the low T regime we found τ⁻¹ ∝ (k_BT)⁴ but with a different prefactor (i.e. ∼3 times smaller) in comparison with the existing quasi-elastic expressions. Furthermore, we found a simple analytic “semi-inelastic” expression of the form τ⁻¹ ∝ (k_BT)⁴/(1 + cT³) which matches nearly perfectly with the full inelastic results for any temperature up to 500 K and μ up to 1 eV. Our simple analytical results agree well with previous first-principles studies and available experimental data. Moreover, we obtain an analytical form for the acoustic gauge field 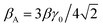. Our analyses pave a way for investigating scatterings between electrons and other fundamental excitations with linear dispersion relation in 2D Dirac material-based heterostructures such as bogolon-mediated electron scattering in graphene-based hybrid Bose–Fermi systems.