Twist dynamics and buckling instability of ring DNA: the effect of groove asymmetry and anisotropic bending

Abstract

By combining analytical theory and Molecular Dynamics simulations we study the relaxation dynamics of DNA circular plasmids that initially undergo a local twist perturbation. In this process, the twist–bend coupling arising from the groove asymmetry in the DNA double helix clearly shows up. In the two scenarios explored, with/without this coupling, the initial perturbation relaxes diffusively. However, there are some marked differences in the value of the diffusion coefficient and the dynamics in both cases. These differences can be explained by assuming the existence of three distinctive time scales; 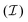a rapid relaxation of local bending, 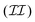the slow twist spreading, and 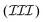the buckling transition taking place in a much longer time scale. In particular, the separation of time scales allows deducing an effective diffusion equation in stage 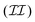, with a diffusion coefficient influenced by the twist–bend coupling. We also discuss the mapping of the realistic DNA model to the simpler isotropic twistable worm-like chain using the renormalized bending and twist moduli; although useful in many cases, it fails to make a quantitative prediction on the instability mode of buckling transition.