Impulse response function for Brownian motion

Abstract

Motivated from the central role of the mean-square displacement and its second time-derivative – that is the velocity autocorrelation function 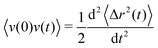in the description of Brownian motion and its implications to microrheology, we revisit the physical meaning of the first time-derivative of the mean-square displacement of Brownian particles. By employing a rheological analogue for Brownian motion, we show that the time-derivative of the mean-square displacement 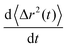of Brownian microspheres with mass m and radius R immersed in any linear, isotropic viscoelastic material is identical to 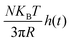, where h(t) is the impulse response function (strain history γ(t), due to an impulse stress τ(t) = δ(t − 0)) of a rheological network that is a parallel connection of the linear viscoelastic material with an inerter with distributed inertance 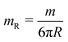. The impulse response function 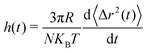of the viscoelastic material-inerter parallel connection derived in this paper at the stress–strain level of the rheological analogue is essentially the response function 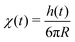of the Brownian particles expressed at the force–displacement level by Nishi et al. after making use of the fluctuation–dissipation theorem. By employing the viscoelastic material-inerter rheological analogue we derive the mean-square displacement and its time-derivatives of Brownian particles immersed in a viscoelastic material described with a Maxwell element connected in parallel with a dashpot and we show that for Brownian motion of microparticles immersed in such fluid-like materials, the impulse response function h(t) maintains a finite constant value in the long term.