Hydrodynamics induce superdiffusive jumps of passive tracers along critical paths of random networks and colloidal gels
Abstract
We present a numerical study on the effect of hydrodynamic interactions (HI) on the diffusion of inert point tracer particles in several fixed random structures. As expected, the diffusion is hampered by the extra hydrodynamic friction introduced by the obstacle network. However, a non-trivial effect due to HI appears in the analysis of the van-Hove displacement probability close to the percolation threshold, where tracers diffuse through critical fractal paths. We show that the tracer dynamics can be split up into short and long jumps, the latter being ruled by either exponential or Gaussian van Hove distribution tails. While at short time HI slow down the tracer diffusion, at long times, hydrodynamic interactions with the obstacles increase the probability of longer jumps, which circumvent the traps of the labyrinth more easily. Notably, the relation between the anomalous diffusion exponent and the fractal dimension of the critical (intricate) paths 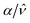 is greater than one, which implies that the long-time (long-jump) diffusion is mildly superdiffuse. A possible reason for such a hastening of the diffusion along the network corridors is the hydrodynamically induced mobility anisotropy, which favours displacements parallel to the walls, an effect which has already been experimentally observed in collagen gels.
is greater than one, which implies that the long-time (long-jump) diffusion is mildly superdiffuse. A possible reason for such a hastening of the diffusion along the network corridors is the hydrodynamically induced mobility anisotropy, which favours displacements parallel to the walls, an effect which has already been experimentally observed in collagen gels.



 Please wait while we load your content...
Please wait while we load your content...