Universal non-Debye low-frequency vibrations in sheared amorphous solids

Abstract

We study energy minimised configurations of amorphous solids with a simple shear degree of freedom. We show that the low-frequency regime of the vibrational density of states of structural glass formers is crucially sensitive to the macroscopic stress of the sampled configurations. In both two and three dimensions, shear-stabilised configurations display a D(ω_min) ∼ ω⁵_min regime, as opposed to the ω⁴_min regime observed under unstrained conditions. In order to isolate the source of these deviations from crystalline behaviour, we also study configurations of two dimensional, strained amorphous solids close to a plastic event. We show that the minimum eigenvalue distribution at a strain ‘γ’ near the plastic event occurring at ‘γ_P’ assumes a universal form that displays a collapse when scaled by 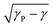, and with the number of particles as N^−0.22. Notably, at low frequencies, this scaled distribution displays a robust D(ω_min) ∼ ω⁶_min power-law regime, which survives in the large N limit. Finally, we probe the properties of these configurations through a characterisation of the second and third eigenvalues of the Hessian matrix near a plastic event.