The role of non-affine deformations in the elastic behavior of the cellular vertex model
Abstract
The vertex model of epithelia describes the apical surface of a tissue as a tiling of polygonal cells, with a mechanical energy governed by deviations in cell shape from preferred, or target, area, A0, and perimeter, P0. The model exhibits a rigidity transition driven by geometric incompatibility as tuned by the target shape index, 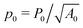 . For
. For 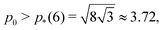 with p*(6) the perimeter of a regular hexagon of unit area, a cell can simultaneously attain both the preferred area and preferred perimeter. As a result, the tissue is in a mechanically soft compatible state, with zero shear and Young's moduli. For p0 < p*(6), it is geometrically impossible for any cell to realize the preferred area and perimeter simultaneously, and the tissue is in an incompatible rigid solid state. Using a mean-field approach, we present a complete analytical calculation of the linear elastic moduli of an ordered vertex model. We analyze a relaxation step that includes non-affine deformations, leading to a softer response than previously reported. The origin of the vanishing shear and Young's moduli in the compatible state is the presence of zero-energy deformations of cell shape. The bulk modulus exhibits a jump discontinuity at the transition and can be lower in the rigid state than in the fluid-like state. The Poisson's ratio can become negative which lowers the bulk and Young's moduli. Our work provides a unified treatment of linear elasticity for the vertex model and demonstrates that this linear response is protocol-dependent.
with p*(6) the perimeter of a regular hexagon of unit area, a cell can simultaneously attain both the preferred area and preferred perimeter. As a result, the tissue is in a mechanically soft compatible state, with zero shear and Young's moduli. For p0 < p*(6), it is geometrically impossible for any cell to realize the preferred area and perimeter simultaneously, and the tissue is in an incompatible rigid solid state. Using a mean-field approach, we present a complete analytical calculation of the linear elastic moduli of an ordered vertex model. We analyze a relaxation step that includes non-affine deformations, leading to a softer response than previously reported. The origin of the vanishing shear and Young's moduli in the compatible state is the presence of zero-energy deformations of cell shape. The bulk modulus exhibits a jump discontinuity at the transition and can be lower in the rigid state than in the fluid-like state. The Poisson's ratio can become negative which lowers the bulk and Young's moduli. Our work provides a unified treatment of linear elasticity for the vertex model and demonstrates that this linear response is protocol-dependent.



 Please wait while we load your content...
Please wait while we load your content...