Analysis of the heat transfer fluctuations in the Rayleigh–Bénard convection of concentrated emulsions with finite-size droplets

Abstract

Employing numerical simulations, we provide an accurate insight into the heat transfer mechanism in the Rayleigh–Bénard convection of concentrated emulsions with finite-size droplets. We focus on the unsteady dynamics characterizing the thermal convection of these complex fluids close to the transition from conductive to convective states, where the heat transfer phenomenon, expressed in terms of the Nusselt number Nu, is characterized by pronounced fluctuations triggered by collective droplet motion [F. Pelusi et al., Soft Matter, 2021, 17(13), 3709–3721]. By systematically increasing the droplet concentration, we show how these fluctuations emerge along with the segregation of “extreme events” in the boundary layers, causing intermittent bursts in the heat flux fluctuations. Furthermore, we quantify the extension S and the duration 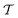of the coherent droplet motion accompanying these extreme events via a suitable statistical analysis involving the droplet displacements. We show how the increase in droplet concentration results in a power-law behaviour of the probability distribution function of S and 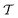and how this outcome is robust at changing the analysis protocol. Our work offers a comprehensive picture, linking macroscopic heat transfer fluctuations with the statistics of droplets at the mesoscale.