Influence of pseudo-Jahn–Teller activity on the singlet–triplet gap of azaphenalenes

Abstract

We analyze the possibility of symmetry-lowering induced by pseudo-Jahn–Teller interactions in six previously studied azaphenalenes that are known to have their first excited singlet state (S₁) lower in energy than the triplet state (T₁). The primary aim of this study is to explore whether Hund's rule violation is observed in these molecules when their structures are distorted from C_2v or D_3h point group symmetries by vibronic coupling. Along two interatomic distances connecting these point groups to their subgroups C_s or C_3h, we relaxed the other internal degrees of freedom and calculated two-dimensional potential energy subsurfaces. The many-body perturbation theory (MP2) suggests that the high-symmetry structures are the energy minima for all six systems. However, single-point energy calculations using the coupled-cluster method (CCSD(T)) indicate symmetry lowering in four cases. The singlet–triplet energy gap plotted on the potential energy surface also shows variations when deviating from high-symmetry structures. A full geometry optimization at the CCSD(T) level with the cc-pVTZ basis set reveals that the D_3h structure of cyclazine (1AP) is a saddle point, connecting two equivalent minima of C_3h symmetry undergoing rapid automerization. The combined effects of symmetry lowering and high-level corrections result in a nearly zero singlet–triplet gap for the C_3h structure of cyclazine. Azaphenalenes containing nitrogen atoms at electron-deficient sites – 2AP, 3AP, and 4AP – exhibit more pronounced in-plane structural distortion; the effect is captured by the long-range exchange-interaction corrected DFT method, ωB97XD. Excited state calculations of these systems indicate that in their low-symmetry energy minima, T₁ is indeed lower in energy than S₁, upholding the validity of Hund's rule. Jahn–Teller analysis predicts the symmetries of the in-plane distortion vibrational modes as 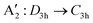or B₂: C_2v → C_s agreeing with the vibrational frequencies of the saddle-points.