Novel turbulence and coarsening arrest in active-scalar fluids
Abstract
We uncover a new type of turbulence – activity-induced homogeneous and isotropic turbulence – in a model that has been employed to investigate motility-induced phase separation (MIPS) in a system of microswimmers. The active Cahn–Hilliard–Navier–Stokes (CHNS) equations, also called active model H, provide a natural theoretical framework for our study. In this CHNS model, a single scalar order parameter ϕ, positive (negative) in regions of high (low) microswimmer density, is coupled with the velocity field u. The activity of the microswimmers is governed by an activity parameter ζ that is positive for extensile swimmers and negative for contractile swimmers. With extensile swimmers, this system undergoes complete phase separation, which is similar to that in binary-fluid mixtures. By carrying out pseudospectral direct numerical simulations (DNSs), we show, for the first time, that (a) this model develops an emergent nonequilibrium, but statistically steady, state (NESS) of active turbulence, for the case of contractile swimmers, if ζ is sufficiently large and negative, and (b) this turbulence arrests the phase separation. We quantify this suppression by showing how the coarsening-arrest length scale does not grow indefinitely, with time t, but saturates at a finite value at large times. We characterise the statistical properties of this active-scalar turbulence by employing energy spectra and fluxes and the spectrum of ϕ. For sufficiently high Reynolds numbers, the energy spectrum 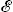 (k) displays an inertial range, with a power-law dependence on the wavenumber k. We demonstrate that, in this range, the flux Π(k) assumes a nearly constant, negative value, which indicates that the system shows an inverse cascade of energy, even though energy injection occurs over a wide range of wavenumbers in our active-CHNS model.
(k) displays an inertial range, with a power-law dependence on the wavenumber k. We demonstrate that, in this range, the flux Π(k) assumes a nearly constant, negative value, which indicates that the system shows an inverse cascade of energy, even though energy injection occurs over a wide range of wavenumbers in our active-CHNS model.



 Please wait while we load your content...
Please wait while we load your content...