Unveiling unique scaling behavior in miscible, volatile Marangoni spreading

Abstract

We present a novel observation of the expansion of the outer tip radius of a fast-spreading ethanol–water film spreading over a deep substrate of water. The experimentally measured radius of the outer tip of the film (r_o) and its velocity (U_o) display a complex scaling with time and drop properties. The variation showed by r_o differed from the commonly observed scalings of t^3/4 and t^1/4. We propose novel scaling laws for r_o and U_o by expressing r_o as the sum of the radius of the stable part of the film r_f and the length of the unstable part l_p at the periphery of the stable part of the film, that had azimuthally uniformly spaced plumes. The radius of the stable part of the film scales as r_f ∼ t^1/4 since, while the film expands, the Marangoni stresses are balanced by viscous stresses within the film thickness. At the same time, l_p ∼ t^3/4 since the plumes grow at the periphery of the stable part of the film, with the driving surface tension stresses balanced by the viscous stresses in a shear layer below the plumes. Combining these two scaling laws yielded a novel, two-term scaling law for r_o, which is close to a single power-law scaling r_o ∼ t^1/2. 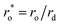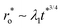We obtain an expression for the dimensionless mean outer tip radius as , where t* = t/t_ξ, t_ξ = (r_d⁴ρ_wμ_w/Δσ²)^1/3 being the time scale. Similarly, we show that the dimensionless velocity scales as 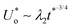with the variables λ₁ and λ₂ being functions of t* and drop properties. These proposed scaling laws are shown to match our measurements, thereby validating the phenomenology of such miscible, volatile spreading.