Mechanism of direct oxidation of cyclohexene to cyclohexanone with nitrous oxide. Theoretical analysis by DFT method
Vasilii I.
Avdeev
*,
Sergey Ph.
Ruzankin
and
Georgii M.
Zhidomirov
Boreskov Institute of Catalysis, Novosibirsk 630090, Russia. E-mail: via@catalysis.nsk.su
First published on 22nd November 2002
Abstract
New very effective results on the liquid-phase oxidation of cyclohexene to cyclohexanone by nitrous oxide are analyzed using the B3LYP/6-31G* approximation to predict a two-step reaction mechanism correlated with the experimental data.
In the last decade nitrous oxide (N2O) has attracted growing attention as a selective oxygen donor for oxidation reactions in the gas phase.1–4 Recently, Panov et al.5,6 described also the liquid-phase oxidation of alkenes by N2O with nearly 100% selectivity. This approach has been exemplified by the oxidation of cyclohexene to cyclohexanone5 and cyclopentene to cyclopentanone.6 The lack of a need to use catalysts and solvents coupled with very high selectivity makes these reactions very promising for practical applications. However, their reaction mechanism is not clear and its theoretical investigation may be rather useful.
This work is the first attempt to elucidate the total mechanistic route of cyclohexene oxidation using the experimental data.5 The authors5,7 postulated the oxidation of double bond C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C to proceed via the intermediate formation of 1,2,3-oxadiazoline. The 1,3-dipolar cycloaddition was analyzed in a number of theoretical studies.8 The DFT calculations of cycloaddition of 16-electron 1,3-dipoles with ethylene showed that these reactions are exothermic.8 Note that the subsequent rearrangement and N2 cleavage were not discussed in the above works.
C to proceed via the intermediate formation of 1,2,3-oxadiazoline. The 1,3-dipolar cycloaddition was analyzed in a number of theoretical studies.8 The DFT calculations of cycloaddition of 16-electron 1,3-dipoles with ethylene showed that these reactions are exothermic.8 Note that the subsequent rearrangement and N2 cleavage were not discussed in the above works.
In the present study we analyze the paths of cyclohexene oxidation to cyclohexanone by nitrous oxide via N2O cycloaddition to cyclohexene or formation of cyclohexene epoxide intermediate. To provide further conversion of cyclohexene epoxide to cyclohexanone, high activation energy should be overcome. At the same time we have found a direct route of 1,2,3-oxadiazoline transformation to cyclohexanone with a reasonable value of activation energy E* = 22 kcal mol−1.
The calculations were carried out using the GAUSSIAN98 program package9 within the Density Functional Theory approach10 with the Becke three-parameter exchange functional within the gradient corrections,11,12 and the Lee-Yang-Parr correlation functional13 with the 6-31G* basis set14 (B3LYP/6-31G* approximation). For the identification of transition states (TS) we have used the QST2 method with the subsequent calculation of frequency’s normal modes and intrinsic reaction coordinate (IRC). This approximation, as numerous calculations of similar systems show,15 provides a good description of energy parameters (reaction heats, reaction routes, and activation energies), equilibrium geometry structures, and vibration frequencies. As was found in the calculations of 1,3-dipolar cycloaddition of N2O to an ethylene molecule,8 this approach gives results which are close to those of the considerably more expensive CCSD(T) level.
The calculations predict a two-step mechanism of the reaction. Fig. 1 shows the energy profile of the steps and basic structural parameters of the stable intermediates and reaction product. Actually, the cycloaddition reaction of 1,3-dipolar to cyclohexene with nitrous oxide8,16 is the first step. The direct interaction between cyclohexene and N2O (reactants R) results in the opening of double bond C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and formation of intermediate dihydro-1:2:3-oxadiazoline (INT1), which includes heterocycle C–N
C and formation of intermediate dihydro-1:2:3-oxadiazoline (INT1), which includes heterocycle C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–O–C with bonds N–N = 1.23 Å and N–O = 1.43 Å. These bond lengths essentially differ from those of the N2O molecule: N–N = 1.14 Å and N–O = 1.19 Å. Note that stability of intermediate INT1 with respect to reagents (ΔH1 = −7.7 kcal mol−1) is probably sufficient for experimental detection at low temperatures. The carbon framework is in trans-configuration. The transition from reactants R to INT1 is an activated process, R → TS1 → INT1. This reaction route probably involves formation of a precursor complex preceding transition state TS1, as shown elsewhere.8 Since the stability of this complex is ca. 1 kcal mol−1, activation energy of this step is determined in general by the energy of transition state TS1 (E* = 27 kcal mol−1). The calculations of vibration frequencies of TS1 and IRC show that this TS1 actually binds initial reagents R and INT1, its single imaginary frequency is ν(TS1) = 452i cm−1.
N–O–C with bonds N–N = 1.23 Å and N–O = 1.43 Å. These bond lengths essentially differ from those of the N2O molecule: N–N = 1.14 Å and N–O = 1.19 Å. Note that stability of intermediate INT1 with respect to reagents (ΔH1 = −7.7 kcal mol−1) is probably sufficient for experimental detection at low temperatures. The carbon framework is in trans-configuration. The transition from reactants R to INT1 is an activated process, R → TS1 → INT1. This reaction route probably involves formation of a precursor complex preceding transition state TS1, as shown elsewhere.8 Since the stability of this complex is ca. 1 kcal mol−1, activation energy of this step is determined in general by the energy of transition state TS1 (E* = 27 kcal mol−1). The calculations of vibration frequencies of TS1 and IRC show that this TS1 actually binds initial reagents R and INT1, its single imaginary frequency is ν(TS1) = 452i cm−1.
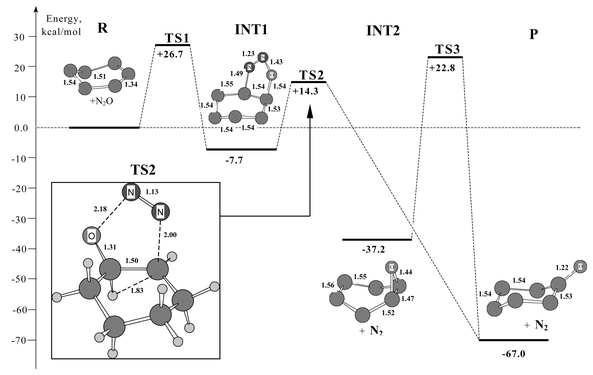 | ||
| Fig. 1 Profile of energy surface R → TS1 → INT1 → TS2 → P (R → cyclohexene + N2O, P→ cyclohexanone + N2) for the two-step mechanism of direct oxidation of cyclohexene to cyclohexanone with nitrous oxide. Relative energies are measured from reactants. | ||
The process of INT1 formation was studied by scanning bond length r = C–O. For r > 3.0 Å, an N2O molecule is linear and normal to the carbon cycle. The molecule parameters are close to those in the gas phase, and angle CON is equal to 180°. When N2O approaches to cyclohexene, starting with r < 3.0 Å, CON reduces to 90° and angle NNO decreases to 135° at a time. For C–O = 2.17 Å, the system reaches transition state TS1, the structure of the five-membered heterocycle is similar to that of heterocycle INT1 (the structure is shown in Fig. 1), and its parameters are as follows: N–N = 1.18 Å, N–O = 1.24 Å, C–N = 2.01 Å, C–O = 2.17 Å, C–C = 1.40 Å. Note that close parameters were obtained by Su et al.8 for the cycloaddition reaction of ethylene to N2O. It is possible to guess that the first step of oxidation of both aliphatic and cyclic olefins proceeds through transition states of a similar structure.
The second step involves the subsequent decomposition of INT1, formation of the target product (P), cyclohexanone, due to transition of hydrogen within the carbon cycle: OC1H1–C2H → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1–C2H2. The process is also activated: INT1 → TS2 → P. For C2–H1 = 1.83 Å, the system reaches transition state TS2 (the TS2 parameters are shown in Fig. 1). This hydrogen shift is responsible for significant changes in the structure of both carbon ring and the five-membered heterocycle. In this case, the carbon bound with oxygen changes its hybridization sp3
→ sp2, providing a shift of electron density to π-bond O
C1–C2H2. The process is also activated: INT1 → TS2 → P. For C2–H1 = 1.83 Å, the system reaches transition state TS2 (the TS2 parameters are shown in Fig. 1). This hydrogen shift is responsible for significant changes in the structure of both carbon ring and the five-membered heterocycle. In this case, the carbon bound with oxygen changes its hybridization sp3
→ sp2, providing a shift of electron density to π-bond O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, cleavage of the N–O bond in the heterocycle (N–O = 2.18 Å for TS2), removal of a nitrogen molecule into the gas phase (C–N = 2.00 Å and N–N = 1.13 Å for TS2). For the second step, the calculated parameters are: ν(TS2) = 437i cm−1, and E* = 22 kcal mol−1.
C, cleavage of the N–O bond in the heterocycle (N–O = 2.18 Å for TS2), removal of a nitrogen molecule into the gas phase (C–N = 2.00 Å and N–N = 1.13 Å for TS2). For the second step, the calculated parameters are: ν(TS2) = 437i cm−1, and E* = 22 kcal mol−1.
Bridson-Jones et al.7 suggested that cyclohexene epoxide might be an intermediate of the reaction of olefin oxidation by N2O. We have studied this reaction route. The calculations suggest two stable cis- and trans-isomers of cyclohexene epoxide. The stability of the cis-isomer is higher than that of trans-isomer by 2.5 kcal mol−1. If one assumes that the cis-isomer is an intermediate INT2 (see Fig. 1), then transition INT2 → P proceeds through transition state TS3. The calculated parameters are: ν(TS3) = 690i cm−1, and E* = 60 kcal mol−1. The analysis of IRC shows that TS3 binds INT2 and P. The overall reaction R → TS1 → INT1 → TS2; INT2 → TS3 → P (see Fig. 1) is −67 kcal mol−1 exothermic.
The first step of the reaction can be considered as the activation of a nitrous oxide molecule, providing the N2O decomposition and creation of active oxygen through formation of an adduct with cyclohexene (INT1). As Fig. 1 suggests, bonds N–N = 1.23 Å and N–O = 1.43 Å are significantly weakened compared to the initial molecule. Electron density is rearranged so that oxygen gets electrophilic properties, which promotes an opening of double bond C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and formation of two new bonds: C–O = 1.45 Å and C–N = 1.49 Å. We believe this is a limiting step that determines the activation energy of the overall reaction. Panov et al. have shown that E* = 21 kcal mol−1 for the oxidation reaction of cyclopentene to cyclopentanone.6 It should be noted that the reaction proceeds under milder conditions compared to the oxidation of cyclohexene, for which one should expect a higher activation energy. According to our estimation, E* = 27 kcal mol−1. It is important that INT1 is a weakly bound intermediate (ΔH1 = −7.7 kcal mol−1), which predetermines a low value of the activation energy of the next step.
C and formation of two new bonds: C–O = 1.45 Å and C–N = 1.49 Å. We believe this is a limiting step that determines the activation energy of the overall reaction. Panov et al. have shown that E* = 21 kcal mol−1 for the oxidation reaction of cyclopentene to cyclopentanone.6 It should be noted that the reaction proceeds under milder conditions compared to the oxidation of cyclohexene, for which one should expect a higher activation energy. According to our estimation, E* = 27 kcal mol−1. It is important that INT1 is a weakly bound intermediate (ΔH1 = −7.7 kcal mol−1), which predetermines a low value of the activation energy of the next step.
The second step governs the nature of the desired product. We have considered only two probable products, cyclohexanone and cyclohexene oxide. At catalytic liquid-phase oxidation of alkenes with N2O, the reaction channel with formation of epoxides is possible.17,18 In the case of non-catalytic oxidation, this channel is eliminated. Actually, our calculations have shown that there is no reaction channel connecting INT1 and cyclohexene epoxide (INT2), and so, if cyclohexene epoxide forms under the given reaction conditions, it transforms into cyclohexanone, INT2 → TS3 → P. It was shown above that the barrier height for TS3 is high enough (ca. 60 kcal mol−1), which excludes this reaction route. This result agrees with the conclusion by Panov et al.5 that cyclohexene oxide introduced into the reaction mixture is not involved in the chemical transformation. Thus, cyclohexanone is the only product of oxidation of cyclohexene with nitrous oxide.
We express our gratitude to G. I. Panov for his stimulating interest in our theoretical results and his useful comments on the experimental investigations quoted in the present report.
This work was supported by INTAS-RFBR (IR-97-1071) and RFBR 00-15-97441.
Notes and references
- G. I. Panov, A. S. Kharitonov and V. I. Sobolev, Appl. Catal. A, General, 1993, 98, 1 CrossRef CAS.
- A. Reitzmann, M. Hafele and G. Emig, Trends Chem. Eng., 1996, 3, 63 Search PubMed.
- G. I. Panov, CATTECH, 2000, 4, 18 Search PubMed.
- A. V. Leontiev, O. A. Fomicheva, M. V. Proskurnina and N. S. Zefirov, Russ. Chem. Rev., 2001, 70, 91 (English) RSC.
- G. I. Panov, K. A. Dubkov, E. V. Starokon and V. N. Parmon, React. Kinet. Catal. Lett., 2002, 76, 401 Search PubMed.
- K. A. Dubkov, G. I. Panov, E. V. Starokon and V. N. Parmon, React. Kinet. Catal. Lett., 2002, 77, 197 Search PubMed.
- F. S. Bridson-Jones, G. D. Buckley, L. H. Cross and A. P. Driver, J. Chem. Soc., 1951, 2999 RSC.
- M. D. Su, H. Yi. Liao, W. S. Chung and S. Y. Chu, J. Org. Chem., 1999, 64, 6710 CrossRef CAS , and references therein.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, P. Salvador, J. J. Dannenberg, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98 (Revision A.11), Gaussian, Inc., Pittsburgh, PA, 2001 Search PubMed.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- R. Krishnan, J. S. Seger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- J. Baker, M. Muir, J. Andzelm and A. Scheiner, Chemical Applications of Density Functional Theory, eds. B. B. Laird, R. B. Ross and T. Ziegler, ACS Symp. Ser. 629, Am. Chem. Soc., Washington, DC, 1996 Search PubMed.
- R. Huisgen, 1,3-Dipolar Cycloaddition Chemistry, ed. A. Padwa, John Wiley & Sons, New York, 1984, vol. 1 Search PubMed.
- T. Yamada, K. Hashimoto, Y. Kitaichi, K. Suzuki and T. Ikeno, Chem. Lett., 2001, 3, 268 CrossRef.
- R. Ben-Daniel, L. Weiner and R. Neumann, J. Am. Chem. Soc., 2002, 124, 8788 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2003 |
