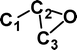
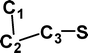
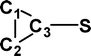
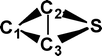
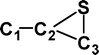
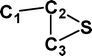
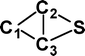
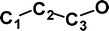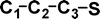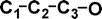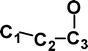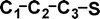Do the interstellar molecules CCCO and CCCS rearrange when energised?
Khoa Minh
Tran
,
Andrew M.
McAnoy
and
John H.
Bowie
Department of Chemistry, The University of Adelaide, South Australia 5005
First published on 27th February 2004
Abstract
Neutrals CCCO, CC13CO, CCCS and CC13CS have been prepared by one-electron vertical (Franck–Condon) oxidation of the precursor anion radicals (CCCO)−˙, (CC13CO)−˙, (CCCS)−˙ and (CC13CS)−˙ respectively in collision cells of a reverse sector mass spectrometer. Ionisation of the neutrals to decomposing cations shows the neutrals to be stable for the microsecond duration of the neutralisation–ionisation (−NR+) experiment. No rearrangement of the label in energised CC13CO or CC13CS occurs during these experiments. In contrast, minor rearrangement of (CC13CO)+˙ is observed [(CC13CO)+˙ → (OCC13C)+˙], while significant rearrangement occurs for (CC13CS)+˙ [(CC13CS)+˙ → (SCC13C)+˙]. Theoretical calculations at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory show that the cationic rearrangements occur by stepwise processes via key rhombic structures. Overall, the degenerate processes result in O and S migration from C-3 to C-1. The cations (CCCO)+˙ and (CCCS)+˙ require excess energies of ≥ 516 and ≥ 226 kJ mol−1 respectively to effect rearrangement.
Introduction
Small cumulenes and heterocumulenes may be formed by neutralisation–ionisation processes (−NR+) from anions in a reverse sector mass spectrometer equipped with a dual collision cell assembly.1 One of the interesting features of these experiments is when these neutrals are energised, some may undergo rearrangement of the carbon skeleton. Particular examples of this behaviour are (i) CCCC2 and CCCCC,3 both of which undergo randomisation of the carbon atoms via rhombic intermediates, and (ii) NCCCN, which scrambles both N and C.4Many cumulenes and heterocumulenes have been detected in interstellar dust clouds, and in circumstellar envelopes of carbon-rich suns.5–9 Two of the most abundant heterocumulenes to be reported are CCCO and CCCS. Sulfur compounds are particularly interesting since they are often more abundant than their oxygen analogues, even though the cosmic abundance of sulfur is less than that of oxygen.10–12
The aim of this study is to make CC13CO and CC13CS, and, using the neutralisation–reionisation (−NR+) technique as a probe, to determine whether any rearrangement occurs for energised neutrals. We are interested in comparing these two systems for two reasons: (i) because of the cumulene rearrangements described above, and (ii) because rearrangements occur for the related systems CCCHO and CCCHS. In the former case, CCCHO rearranges to HCCCO by H rearrangement,13 whereas CCCHS rearranges to HCCCS by competitive H and S rearrangement.14 Perhaps CCCS may undergo S rearrangement, but CCCO will be stable?
Neutral CCCO has been detected [together with the related propynal (HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–CHO), from which CCCO may be formed] in the dark molecular cloud TMC-1.15 It has been made by a number of methods,16–19 including neutralisation of [CCCO]+˙17 and [CCCO]−˙.19 A number of theoretical studies have been devoted to cumulene oxides (including CCCO),20–25 and their rotational spectra have been measured.26,27 There are two stable forms of CCCO: the 1Σ singlet ground state is linear,27 while the 3A′ triplet state is bent and 271 kJ less stable than the ground state singlet (at the RCCSD(T)/aug-cc-pVDZ//B3LYP/6-31+G* level of theory).19
C–CHO), from which CCCO may be formed] in the dark molecular cloud TMC-1.15 It has been made by a number of methods,16–19 including neutralisation of [CCCO]+˙17 and [CCCO]−˙.19 A number of theoretical studies have been devoted to cumulene oxides (including CCCO),20–25 and their rotational spectra have been measured.26,27 There are two stable forms of CCCO: the 1Σ singlet ground state is linear,27 while the 3A′ triplet state is bent and 271 kJ less stable than the ground state singlet (at the RCCSD(T)/aug-cc-pVDZ//B3LYP/6-31+G* level of theory).19
Sulfur carbon clusters occur in both dark clouds and circumstellar envelopes.28–30 Neutral CCCS has been detected in the circumstellar envelope of the star IRC+1021631,32 and has been synthesised in the laboratory.32,33 A number of theoretical studies on CCCS have been reported,28,29,32,34 and it has been proposed that CCCS may be formed from the interstellar radical CCCH, as shown in eqn. (1).34
| CCCH˙ + S → CCCS + H˙ | (1) |
Results and discussion
Syntheses of the anion precursors
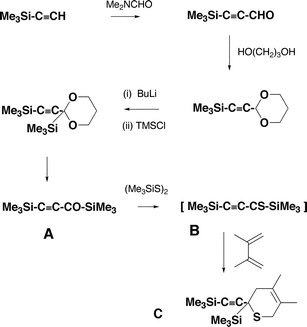
The most important part of this project involves the synthesis of the precursor neutrals which will be used to make (CCCO)−˙, (CCCS)−˙ and their labelled analogues (CC13CO)−˙ and (CC13CS)−˙. In our previous synthesis of (CCCO)−˙, we used TMSC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–CO–Et as the precursor neutral. This is not suitable for the preparation of 13C labelled precursors, so we undertook the synthetic procedures shown in Scheme 1.
C–CO–Et as the precursor neutral. This is not suitable for the preparation of 13C labelled precursors, so we undertook the synthetic procedures shown in Scheme 1.
 | ||
| Scheme 1 | ||
The syntheses commence with the TMS derivative of acetylene, which is allowed to react with dimethylformamide to yield the aldehyde. The aldehyde is converted to the acetal which on base treatment allows the addition of the second TMS group. Hydrolysis of the acetal furnishes the bis TMS ketone A, which is the precursor of (CCCO)−˙. The ketone A can be converted into the thioketone B by reaction with bis TMS disulfide. However the thioketone B is unstable, and is trapped in situ to form the Diels–Alder adduct C. This species is used (as shown below) to produce (CCCS)−˙. The same sequence was used for the formation of the two 13C labelled precursor molecules. The label is introduced in the first step of the synthesis, i.e. by the reaction between TMS acetylene and Me2N13CHO.
Syntheses and stabilities of (CCCO)−˙ and (CCCS)−˙ and their labelled analogues
These species are formed from A and C as shown in Scheme 2. In essence, for eqn. (2), F− ions, formed from SF6 on electron capture, effect two SN2(Si) reactions to produce the required (CCCO)−˙. This procedure is an adaptation (using SF62) of a method first reported by Squires35 for systems containing two TMS groups. Equation (2) shows only reactants and products: the actual sequence of the double de-silylation process is not known.35 The process forming (CCCS)−˙ [eqn. (3)] is similar except that a retro Diels–Alder process accompanies the desilylation steps. The sequence of the steps in the formation of (CCCS)−˙ is not known.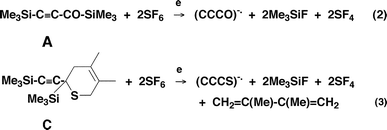 | ||
| Scheme 2 | ||
Before attempting the one-electron oxidations of (CCCO)−˙ and (CCCS)−˙ to the neutrals, it is necessary to be certain that the anions do not rearrange prior to or during the oxidation process. The collision induced mass spectra (MS/MS) of (CCCO)−˙ and (CCCS)−˙ show these radical anions to be very stable. The only fragment peaks in the spectra are of very small abundance. They correspond to loss of CO [from (CCCO)−˙] and the formation of (CS)−˙ [from (CCCS)−˙]. The two labelled anions fragment specifically as shown in eqns. (4) and (5). Thus there is no rearrangement of either system when collisionally activated.
| (CC13CO)−˙ → (CC)−˙ + 13CO | (4) |
| (CC13CS)−˙ → (13CS)−˙ + CC | (5) |
Although the above experimental results show that there is no rearrangement of either (CCCO)−˙ or (CCCS)−˙ during conditions equivalent to those used for the vertical one-electron oxidations of the anions to the neutrals, it is still of interest to examine theoretically how much excess energy is required to effect oxygen and sulfur rearrangement. These reactions have been studied at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory using Gaussian 98. The results are summarised in Figs. 1 and 2, with full details given in Tables 1 and 2. The lowest energy pathway for degenerate oxygen rearrangement is concerted with a barrier to the transition state of 356 kJ mol−1. This is far too high to allow rearrangement of (CCCO)−˙ in the first collision cell of the mass spectrometer. The S system is the more complex of the two (see Fig. 2). In this case there is no low-energy concerted reaction. The rearrangement process is a stepwise sequence proceeding through a “rhombic” transition state 219 kJ mol−1 above (CCCS)−˙. This is more energetically favourable than the oxygen rearrangement shown in Fig. 1. Even so, the process is not observed experimentally under conditions of collisional activation.
![Degenerate rearrangement of (CCCO)−˙. Energies [kJ mol−1, relative to (CCCO)−˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 1.](/image/article/2004/OB/b316867k/b316867k-f1.gif) | ||
| Fig. 1 Degenerate rearrangement of (CCCO)−˙. Energies [kJ mol−1, relative to (CCCO)−˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 1. | ||
![Degenerate rearrangement of (CCCS)−˙. Energies [kJ mol−1, relative to (CCCS)−˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 2.](/image/article/2004/OB/b316867k/b316867k-f2.gif) | ||
| Fig. 2 Degenerate rearrangement of (CCCS)−˙. Energies [kJ mol−1, relative to (CCCS)−˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 2. | ||
|
|
|
|
|---|---|---|
| a Energies are calculated at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory and are relative to CCCO−˙ (−188.9643951 Hartrees). b B3LYP/6-31G(d) geometries. | ||
| State | 2A′ | 2A″ |
| Relative energy (kJ mol−1)a | 0.0 | 356.1 |
| Dipole moment (Debye)b | 3.45 | 2.96 |
| C1C2 (Å) | 1.275 | 1.288 |
| C2C3 | 1.363 | 1.673 |
| C1C3 | 1.928 | |
| C3O | 1.223 | 1.524 |
| C1C2C3 (°) | 167.3 | 80.6 |
| C2C3O | 142.8 | 49.3 |
| C1C2C3O | 180.0 | 180.0 |
|
|
|
|
|
|
|---|---|---|---|---|
| a Energies are calculated at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory and are relative to CCCS−˙ (−511.5816670 Hartrees). b B3LYP/6-31G(d) geometries. | ||||
| State | 2Π | — | 2B2 | 2A″ |
| Relative energy (kJ mol−1)a | 0.0 | 118.3 | 30.3 | 218.7 |
| Dipole moment (Debye)b | 4.17 | 2.36 | 1.59 | 2.74 |
| C1C2 (Å) | 1.302 | 1.334 | 1.366 | 1.411 |
| C2C3 | 1.296 | 1.363 | 1.427 | 1.642 |
| C1C3 | 1.935 | 1.366 | 1.411 | |
| C3S | 1.622 | 1.631 | 1.660 | 1.885 |
| C1C2C3 (°) | 180.0 | 91.7 | 61.4 | 54.4 |
| C2C3S | 180.0 | 167.0 | 151.4 | 64.2 |
| C1C2C3S | 180.0 | −67.0 | 180.0 | 157.2 |
We conclude that the precursor radical anions (CCCO)−˙ and (CCCS)−˙ are suitable precursors to effect one-electron oxidation to CCCO and CCCS.
Neutral CCCO and the radical cation (CCCO)+˙
There are two stable forms of CCCO, the 1Σ linear ground state and the 3A′ bent triplet state. The difference in energy between the two states has been calculated to be 271 kJ mol−1,19 thus we have not considered the triplet state further. The charge reversal (−CR+) and neutralisation–reionisation (−NR+) spectra of (CC13CO)−˙ are shown in Fig. 3: similar data for (CCCO)−˙ are listed in Table 3. The cation in the CR spectrum is produced by synchronous two-electron oxidation of the anion radical. This spectrum shows exclusive loss of 12C, together with major losses of 13CO and 12C12C. This indicates that the majority of the decomposing cation radicals have retained the connectivity (CC13CO)+˙. However, there are minor peaks corresponding to the losses of 12CO and 12C13C that are diagnostic to some rearrangement of the cation to (OCC13C)−˙. The peak areas of these minor peaks (m/z 25 and 28) are about 10% of the major peaks (m/z 24 and 29). The mechanism of the cation rearrangement will be considered later.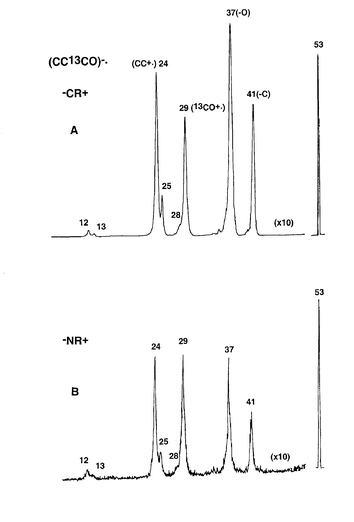 | ||
| Fig. 3 Spectra of (CC13CO)−˙: A) −CR+, B) −NR+. VG ZAB 2HF mass spectrometer. For experimental conditions see Experimental section. | ||
| (CCCO)−˙ | |
|---|---|
| −CR+ | 52(parent)100; 40(C)2.3; 36(O)2.9; 28(C2)1.2; 24(CO)2.0; 12(C2O)0.2 |
| −NR+ | 52(parent)100; 40(C)2.5; 36(O)2.9; 28(C2)2.4; 24(CO)2.2; 12(C2O)0.2 |
| (CCCS)−˙ | |
|---|---|
| −CR+ | 68(parent)100; 56(C)10; 44(C2)3.6; 36(S)0.6; 32(C3)1.6; 24(CS)0.2 |
| −NR+ | 68(parent)100; 56(C)5.5; 44(C2)2.5; 36(S)1.5; 32(C3)1.7; 24(CS)0.2 |
The −NR+ spectrum (Fig. 3B) shows a pronounced parent peak (m/z 53) which indicates that a portion of the neutrals formed by one-electron oxidation are stable for the period of the NR experiment, i.e. ≥ 1 microsecond. The peak ratios of m/z 25 to 24 and m/z 28 to 29 are slightly less in the −NR+ spectrum (in comparison to those observed in the −CR+ spectrum). In addition, m/z 29 and 24 are of larger abundance in the −NR+ spectrum (than the corresponding peaks in the −CR+ spectrum). If neutral rearrangements occur, m/z 25 and 28 would be of greater abundance in the −NR+ than the −CR+ spectrum. Since this is not so, the rearrangement peaks observed in the −NR+ spectrum must originate from the cation, not from neutral CC13CO.
The above data show that CC13CO [formed by neutralisation of (CC13CO)−˙] is a stable species which does not undergo rearrangement during the microsecond duration of the NR experiment. Rearrangement of singlet CCCO has also been studied theoretically at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. The reaction coordinate is shown in Fig. 4 with full details of all minima and transition states listed in Table 4. There is no low energy concerted process (cf.Fig. 1), instead, a high energy stepwise process proceeds through a symmetrical rhombic transition state, which lies 479 kJ mol−1 above singlet CCCO. Experiment and theory agree; there is no facile degenerate rearrangement of singlet CCCO.
![Degenerate rearrangement of singlet CCCO. Energies [kJ mol−1, relative to CCCO, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 4.](/image/article/2004/OB/b316867k/b316867k-f4.gif) | ||
| Fig. 4 Degenerate rearrangement of singlet CCCO. Energies [kJ mol−1, relative to CCCO, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 4. | ||
|
|
|
|
|
|
|---|---|---|---|---|
| a Energies are calculated at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory and are relative to CCCO (−188.9262679 Hartrees). b B3LYP/6-31G(d) geometries. | ||||
| State | 1Σ | 1A′ | 1A′ | 1A′ |
| Relative energy (kJ mol−1)a | 0.0 | 385.6 | 376.4 | 478.6 |
| Dipole moment (Debye)b | 1.95 | 2.66 | 1.88 | 0.55 |
| C1C2 (Å) | 1.278 | 1.282 | 1.296 | 1.428 |
| C2C3 | 1.299 | 1.483 | 1.478 | 1.428 |
| C3O | 1.161 | 1.199 | 1.279 | 1.467 |
| C2O | 1.876 | 1.483 | 1.731 | |
| C1C2C3 (°) | 180.0 | 174.3 | 162.8 | 91.8 |
| C2C3O | 180.0 | 88.1 | 64.6 | 73.4 |
| C1C2C3O | 180.0 | 0.0 | 180.0 | 42.2 |
Why is m/z 29 more abundant in the −NR+ spectrum of (CC13CO)−˙ (see Figs. 3A and 3B)? The reason for this is apparent when the thermochemistries of the decompositions of CCCO and (CCCO)+˙ are considered. These are compared in Table 5. The losses of C and O noted in Fig. 3B are high energy decompositions of the cation. The only possible neutral decomposition is loss of CO from CCCO (+334 kJ mol−1). If some of the neutrals have energies ≥ 334 kJ mol−1 they may decompose to CC and CO. Thus the enhanced abundance of m/z 29 in the −NR+ spectrum of (CC13CO)−˙ is due to dissociation of some neutral CC13CO molecules prior to reionisation. This also explains the smaller abundance of m/z 28 in the −NR+ spectrum, since this is only produced following or accompanying rearrangement of the cation.
The −CR+ and −NR+ spectra of (CC13CO)−˙ show that the doublet cation radical (CC13CO)+˙ does undergo some rearrangement to (OCC13C)+˙. However this rearrangement is minor, and clearly unfavourable. The cation rearrangement has been investigated theoretically. The process is summarised in Fig. 5 with full details listed in Table 6. The cation rearrangement is quite similar to that already described for the neutral. Energetically, it is less favourable than the neutral rearrangement, requiring a minimum of 516 kJ mol−1 to effect the rearrangement. Thus it is not surprising that the cation rearrangement is only a minor process. The cations that rearrange are likely to obtain this excess energy (≥ 516 kJ mol−1) by keV collisions of parent cations occurring subsequent to the Franck–Condon vertical oxidation process.
![Degenerate rearrangement of (CCCO)+˙. Energies [kJ mol−1, relative to (CCCO)+˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 6.](/image/article/2004/OB/b316867k/b316867k-f5.gif) | ||
| Fig. 5 Degenerate rearrangement of (CCCO)+˙. Energies [kJ mol−1, relative to (CCCO)+˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 6. | ||
|
|
|
|
|
|
|---|---|---|---|---|
| a Energies are calculated at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory and are relative to CCCO+˙ (−188.5319672 Hartrees). b B3LYP/6-31G(d) geometries. | ||||
| State | 2Σ | 2A′ | — | 2B2 |
| Relative energy (kJ mol−1)a | 0.0 | 431.9 | 414.9 | 516.1 |
| Dipole moment (Debye)b | 2.73 | 1.38 | 0.57 | 2.21 |
| C1C2 (Å) | 1.221 | 1.239 | 1.347 | 1.389 |
| C2C3 | 1.341 | 1.500 | 1.553 | 1.389 |
| C3O | 1.134 | 1.217 | 1.290 | 1.851 |
| C2O | 1.589 | 1.383 | 1.394 | |
| C1C2C3 (°) | 180.0 | 175.6 | 151.3 | 166.8 |
| C2C3O | 180.0 | 70.7 | 57.3 | 48.4 |
| C1C2C3O | 180.0 | 180.0 | −139.2 | 0.0 |
Neutral CCCS and the radical cation (CCCS)+˙
The −CR+ and −NR+ spectra of (CC13CS)−˙ are shown in Fig. 6: similar data for (CCCS)−˙ are recorded in Table 3. The −NR+ spectrum shows a pronounced peak at m/z 69, indicating that some of the neutrals are stable for at least a microsecond. The −NR+ and −CR+ spectra are similar, with the exception that the peak at m/z 32 (S+˙) is of higher abundance in the −NR+ spectrum. The most important features of the two spectra are that the ratios of the peak areas of m/z 57 : 56 [(C13CS)+˙ to (CCS)+˙] and m/z 44 : 45 [(13CS)+˙ to (CS)+˙] are the same in the two spectra. This means that neutral CC13CS does not rearrange during the microsecond duration of the −NR+ experiment, and that the rearrangement ions observed in the −NR+ spectrum are formed by rearrangement of (CC13CS)+˙. The enhanced peak at m/z 32 in the −NR+ spectrum is due to some CC13CS neutrals having sufficient excess energy to effect dissociation to CC13C and S [the exothermicities of the two processes CCCS → CCC + S and (CCCS)+˙ → (CCC)+˙ + S are +590 and +755 kJ mol−1 respectively (at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory)].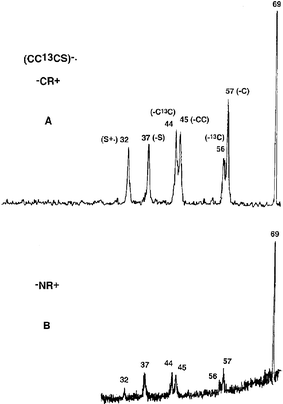 | ||
| Fig. 6 Spectra of (CC13CS)−˙: A) −CR+, B) −NR+. VG ZAB 2HF mass spectrometer. For experimental conditions see Experimental section. | ||
The degenerate rearrangements of CCCS and (CCCS)+˙ have been investigated theoretically. There are two stable forms of CCCS; namely the linear 1Σ singlet and the bent triplet. It has been reported28 that these two structures are separated by 260 kJ mol−1, so we have not considered the triplet structure further. The degenerate stepwise rearrangement of singlet CCCS is shown in Fig. 7, with full details of minima and transition states listed in Table 7. There is no concerted rearrangement of lower energy. The S rearrangement is more favourable than the corresponding O rearrangement of CCCO: CCCS and CCCO require excess energies of ≥ 336 and 479 kJ mol−1 respectively to effect rearrangement. Even so, the S rearrangement is highly energetic in accord with the experimental observation that it does not occur under NR conditions. Interestingly, the reaction proceeds through a key rhombic C3S intermediate (216 kJ mol−1 above CCCS), while the corresponding rhombic species in the CCCO rearrangement is a transition state.
![Degenerate rearrangement of singlet CCCO. Energies [kJ mol−1, relative to CCCS, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 7.](/image/article/2004/OB/b316867k/b316867k-f7.gif) | ||
| Fig. 7 Degenerate rearrangement of singlet CCCO. Energies [kJ mol−1, relative to CCCS, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 7. | ||
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| a Energies are calculated at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory and are relative to CCCS (−511.5287282 Hartrees). b B3LYP/6-31G(d) geometries. | |||||
| State | 1Σ | 1A′ | 1A′ | 1A′ | 1A1 |
| Relative energy (kJ mol−1)a | 0.0 | 336.1 | 266.2 | 278.6 | 216.3 |
| Dipole moment (Debye)b | 3.04 | 4.11 | 2.17 | 2.52 | 2.86 |
| C1C2 (Å) | 1.286 | 1.281 | 1.309 | 1.303 | 1.420 |
| C2C3 | 1.294 | 1.420 | 1.431 | 1.469 | 1.473 |
| C3S | 1.551 | 1.609 | 1.741 | 1.788 | 1.762 |
| C2S | 2.292 | 1.818 | 1.740 | 1.420 | |
| C1C2C3 (°) | 180.0 | 177.8 | 159.4 | 103.9 | 58.7 |
| C2C3S | 180.0 | 98.2 | 69.1 | 63.7 | 65.3 |
| C1C2C3S | 180.0 | 0.0 | 180.0 | 180.0 | 180.0 |
The −CR+ and −NR+ spectra of (CC13CS)−˙ show that significant rearrangement occurs within the parent radical cation. The results of molecular modelling the reaction coordinate of the degenerate rearrangement of (CCCS)+˙ are shown in Fig. 8, with full details of minima and transition states listed in Table 8. The rearrangement is a stepwise process. No lower energy concerted process was found. This stepwise rearrangement is more energetically feasible than any other rearrangements considered in this paper. It is very similar in mechanism to the neutral CCCS rearrangement considered above. The cation requires an excess energy of ≥ 226 kJ mol−1 in order to effect the degenerate rearrangement which proceeds through a symmetrical ‘rhombic’ C3S cation lying 189 kJ mol−1 above CCCS. The neutral and cationic CCCS have very similar geometries (see Tables 6 and 7), thus the excess energy of the cation as a function of the Franck–Condon vertical process will be small. The Franck–Condon excess energy can be calculated since it is the difference in energy between doublet (CCCS)+˙ and of the cation with neutral geometry on the cationic surface. This energy is only 17 kJ mol−1 at the level of theory used in this investigation, hence rearranging (CCCS)+˙ cations must obtain the additional energy by keV collisions with the collision gas in the collision cell.
![Degenerate rearrangement of (CCCS)+˙. Energies [kJ mol−1, relative to (CCCS)+˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 8.](/image/article/2004/OB/b316867k/b316867k-f8.gif) | ||
| Fig. 8 Degenerate rearrangement of (CCCS)+˙. Energies [kJ mol−1, relative to (CCCS)+˙, 0 kJ mol−1] at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory. For details of geometries and energies of minima and transition states see Table 8. | ||
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| a Energies are calculated at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory and are relative to CCCS+˙ (−511.1557742 Hartrees). b B3LYP/6-31G(d) geometries. | |||||
| State | 2Σ | 2A′ | 2A1 | 2A″ | 2A1 |
| Relative energy (kJ mol−1)a | 0.0 | 125.8 | 108.6 | 225.8 | 188.5 |
| Dipole moment (Debye)b | 1.35 | 1.05 | 1.08 | 2.51 | 0.19 |
| C1C2 (Å) | 1.227 | 1.300 | 1.304 | 1.521 | 1.345 |
| C2C3 | 1.336 | 1.453 | 1.511 | 1.554 | 1.509 |
| C1C3 | 1.632 | 1.304 | 1.382 | 1.345 | |
| C3S | 1.510 | 1.533 | 1.542 | 1.646 | 1.757 |
| C2S | 1.914 | 1.757 | |||
| C1C2C3 (°) | 180.0 | 72.5 | 64.5 | 53.4 | 55.9 |
| C2C3S | 180.0 | 161.2 | 154.5 | 73.4 | 64.6 |
| C1C2C3S | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 |
The −NR+ spectrum of (CC13CS)−˙ is weak in comparison to the −CR+ spectrum, but it shows an area ratio of close to 3 : 1 for the losses of C and 13C, and 1 : 1 for losses of CC and C13C. In the case of (CC13CS)+˙, the key intermediate is the ‘rhombic’ structure shown in Scheme 3. This intermediate can ring open to give the two three membered ring systems shown in Scheme 3. Equilibration of this system accompanied by ring opening will give (CC13CS)+˙, (C13CCS)+˙ and (13CCCS)+˙ in the ratio 1 : 1 : 1. This will lead to the decomposition ratios (i) C to 13C loss (2 : 1), and (ii) CC to C13C loss (1 : 2), assuming there is no 13C kinetic isotope effect operating. The experimentally observed ratios indicate that incomplete carbon scrambling accompanies the fragmentations outlined above. The losses of C and CC from (CCCS)+˙ are both high energy processes [+784 to +581 kJ mol−1 respectively (at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-31G(d) level of theory)].
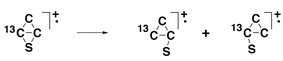 | ||
| Scheme 3 | ||
In conclusion
1 The neutrals CCCO and CCCS can be made by one-electron vertical oxidation of the anion precursors (CCCO)−˙ and (CCCS)−˙.2 The majority of neutrals CCCO and CCCS formed by this Franck–Condon process are stable for at least a microsecond, but a small proportion may decompose to form CC and CO, and S and CCC respectively. Neither oxygen (CCCO to OCCC) nor sulfur rearrangement (CCCS to SCCC) occurs during the NR timeframe.
3 The structures of the neutrals CCCO and CCCS were probed by a consideration of the decompositions of the corresponding cations (produced by ionisation of the neutrals). A minority of the (CCCO)+˙ cations undergo the degenerate rearrangement to (OCCC)+˙.
In contrast, the analogous (CCCS)+˙ to (SCCC)+˙ rearrangement is significant under NR conditions.
4 The reason why CCCS does not undergo S rearrangement while CCCHS does,14 is due to the lower energy requirement for rearrangement of CCCHS [CCCHS (+100 kJ mol−1);14 CCCS (+ 393 kJ mol−1)]. This difference is primarily a consequence of the different geometries of the two systems: for CCCHS and CCCS, the CCS angles are 114.4°14 and 180° respectively.
Experimental section
A Mass spectrometric methods
For a detailed description of the experiment and the instrument used, see.13 In brief, the experiments were performed using a two-sector modified VG ZAB 2HF mass spectrometer with BE configuration, where B and E represent magnetic and electric sectors, respectively. The precursor anions to CCCO and CCCS were formed in the chemical ionisation ion source by the SF6 method2,35 shown in Scheme 2. Typical source conditions were as follows: source temperature 200 °C, repeller voltage −0.5 V, ion extraction voltage 7 kV, mass resolution m/Δm ≥ 1500. Each neutral precursor was inserted into the ion source through the direct probe which was heated to 60 °C to give a measured pressure of ca. 10−6 Torr inside the source housing. The reagent gas SF6 was introduced through a gas inlet into the ion source, to give a measured total pressure of ca. 10−5 Torr in the source housing. The estimated total pressure in the ion source is 10−1 Torr. Collisional induced (CID) spectra of the anions were determined using B to select the parent anion in each case, and utilising argon as the target gas in the first collision cell following B. The pressure of argon in the first cell was maintained such that 80% of the parent ion beam was transmitted through the cell. This corresponds to an average of 1.1–1.2 collisions per ion.36 Product anion peaks resulting from CID processes were recorded by scanning E.Neutralisation–reionisation37–39 (−NR+) experiments were performed for mass-selected anions utilising the dual collision cells located between the magnetic and electric sectors. Neutralisation of anions was effected by collisional electron detachment using O2 at 80% transmittance (of the main beam) as the collision gas in the first collision cell, while reionisation to cations was achieved by collision of the neutrals with O2 (80% transmittance) in the second collision cell. In order to detect a reionisation signal due to the parent neutral, the neutral species must be stable for the one microsecond timeframe of this experiment. Charge reversal (−CR+) spectra40,41 were recorded using single collision conditions in collision cell 1 (O2, 80% transmission of main beam).
B Synthetic procedures
Trimethylsilylpropyn-1-al,42 and 1,3-bis(trimethylsilyl)-2-propyn-1-one,42 were made by standard procedures. {3,6-Dihydro-4,5-dimethyl-2-[(trimethylsilyl)ethynyl]-2H-thiopyran-2-yl}trimethyl silane (intermediate C, Scheme 1) was also made by a standard procedure,43 but spectroscopic data was not reported. This compound has the following spectroscopic data:- υ (cm−1), 2155 (C + C); M+, m/z 296; 1H NMR, δ (CDCl3, 200 mHz): −0.03 (s, 9H, TMS); 0.19 (s, 9H, TMS); 1.12 (m, 2H, CH2C); 1.51 (s, 3H, CH3); 1.56 (s, 3H, CH3); 3.10 (m, 2H, CH2S).C Theoretical methods
Geometry optimisations were carried out with the Becke 3LYP method44,45 using the Dunning aug-cc-pVDZ basis set46 within the GAUSSIAN 98 suite of programs.47 Stationary points were characterised as either minima (no imaginary frequencies) or transition structures (one imaginary frequency) by calculation of the frequencies using analytical gradient procedures. The minima connected by a given transition structure were confirmed by intrinsic reaction coordinate (IRC) calculations. The calculated frequencies were also used to determine zero-point vibrational energies which were used as a zero-point correction for the electronic energies. We have previously reported the success of the B3LYP method in predicting geometries of unsaturated chain structures, and that this method produces optimised structures, at low computational cost, that compare favourably with higher level calculations.48 The B3LYP method provides good agreement with experimental observations of CnS (n = 2–9) molecules.49 More accurate energies for the B3LYP geometries were determined using the CCSD(T) method including zero point energy correction (calculated by vibrational frequencies at the B3LYP/aug-cc-pVDZ level of theory). All calculations were carried out on the Alpha Server at the Australian Partnership for Advanced Computing (APAC) National Facility (Canberra).Acknowledgements
We thank the Australian Research Council for ongoing funding of our negative ion programme. A.M.McA. thanks the ARC for a research associate stipend. We thank the Australian Partnership for Advanced Computing (APAC) National Facility (Canberra) for a generous allowance of time on their super computing facility.References
- S. Dua, S. J. Blanksby, S. Peppe, A. M. McAnoy and J. H. Bowie, Curr. Org. Chem., 2003, 7, 1545 Search PubMed.
- S. J. Blanksby, D. Schröder, S. Dua, J. H. Bowie and H. Schwarz, J. Am. Chem. Soc., 2000, 122, 7105 CrossRef CAS.
- S. Dua and J. H. Bowie, J. Phys. Chem. A, 2002, 106, 1374 CrossRef CAS.
- S. J. Blanksby, S. Dua, J. H. Bowie, D. Schrõder and H. Schwarz, J. Phys. Chem. A, 2000, 104, 11248 CrossRef CAS.
- H. Olofsson, Molecules in the Stellar Environment, Lecture Notes in Physics, ed. O. G. Jorgenson, Springer: Heidelberg, 1994, pp. 114–133 and references cited therein Search PubMed.
- P. F. Bernath, K. H. Hinkle and J. J. Keady, Science, 1989, 244, 562 CAS.
- K. H. Hinkle, Molecules in the Stellar Environment, Lecture Notes in Physics, ed. O. G. Jorgenson, Springer: Heidelberg, 1994, pp. 99–114 and references cited therein Search PubMed.
- D. Smith and P. Spanel, Mass Spectrom. Rev., 1995, 14, 255 CAS.
- S. J. Blanksby and J. H. Bowie, Mass Spectrom. Rev., 1999, 18, 131 CrossRef CAS.
- Y. Hirahara, Y. Ohshima and Y. Endo, Astrophys. J., 1993, 408, L113 CrossRef CAS; Y. Kasai, O. Kinichi, Y. Ohshima, Y. Korahara, Y. Endo, K. Kawaguchi and A. Muramaki, Astrophys. J., 1993, 410, L45 CrossRef CAS.
- V. Trimble, Rev. Mod. Phys., 1975, 47, 877 CrossRef CAS.
- R. D. Brown, Astrophys. J., 1985, 297, 302 CrossRef CAS; M. Ohishi, H. Suzuki, S. Ishikawa, C. Yamada, H. Kanamori, W. M. Irvine, R. D. Brown, P. D. Godfrey and N. Kaifu, Astrophys. J., 1991, 380, L39 CrossRef CAS.
- S. Peppe, S. J. Blanksby, S. Dua and J. H. Bowie, J. Phys. Chem. A, 2000, 104, 5817 CrossRef CAS.
- S. Peppe, S. Dua, A. M. McAnoy and J. H. Bowie, J. Phys. Chem. A, 2003, 107, 1181 CrossRef CAS.
- H. E. Matthews, W. M. Irvine, P. Friberg, R. D. Brown and P. D. Godfrey, Nature, 1984, 310, 125 CAS.
- R. D. Brown, F. W. Eastwood, P. S. Elmes and P. D. Godfrey, J. Am. Chem. Soc., 1983, 105, 6496 CrossRef CAS.
- R. H. Bateman, J. Brown, M. Lefevre, R. Flammang and Y. N. Haverbeke, Int. J. Mass Spectrom. Ion Phys., 1992, 115, 205 Search PubMed.
- S. Ekern and M. Vala, J. Phys. Chem., 1997, 101, 3601 Search PubMed.
- S. J. Blanksby, S. Dua and J. H. Bowie, Rapid Commun. Mass Spectrom., 1999, 13, 2249 CrossRef CAS.
- E. Herbst, D. Smith and G. N. Adams, Astron. Astrophys., 1984, 138, L13 Search PubMed.
- R. D. Brown, P. D. Godfrey, D. M. Cragg, E. H. N. Rice, W. M. Irvine, P. Friberg, H. Suzuki, M. Ohishi, N. Kaifu and M. Morimoto, J. Astrophys., 1985, 297, 302 Search PubMed; R. D. Brown, D. A. McNaughton and K. G. Dyall, Chem. Phys., 1988, 119, 189 CrossRef CAS; R. G. A. R. Maclagan and P. Sudkeaw, J. Chem. Soc., Faraday Trans, 1993, 89, 3325 RSC.
- M. Moazzen-Ahmalsi and F. Zerbetto, J. Chem. Phys., 1995, 103, 6343 CrossRef CAS.
- P. Botschwina, J. Flügge and P. Sebald, J. Phys. Chem., 1995, 99, 9755 CrossRef CAS.
- Y. Ohshima, Y. Endo and T. Ogata, J. Chem. Phys., 1995, 102, 1493 CrossRef CAS; S. J. Blanksby, A. M. McAnoy, S. Dua and J. H. Bowie, Mon. Not. R. Astron. Soc., 2001, 328, 89 CrossRef CAS.
- T. Ogata, Y. Ohshima and Y. Endo, J. Am. Chem. Soc., 1995, 102, 3593 CrossRef.
- R. D. Brown, P. D. Godfrey, P. S. Elmes, M. Rodler and L. M. Tack, J. Am. Chem. Soc., 1985, 107, 4112 CrossRef CAS.
- J. M. Oakes and G. B. Ellison, Tetrahedron, 1986, 42, 6263 CrossRef CAS; J. C. Rienstra-Kiracofe, G. B. Ellison, B. C. Hoffman and H. F. Schaefer, J. Phys. Chem. A, 2001, 104, 2273 CrossRef.
- R. J. Flores, P. I. Juste, L. Carballeira, C. Estevez and F. Gomez, Chem. Phys. Lett., 2001, 343, 105 CrossRef.
- S. Lee, Chem. Phys. Lett., 1997, 268, 69 CrossRef CAS.
- J. Szczepanski, R. Hodyss, J. Fuller and M. Vala, J. Phys. Chem. A, 1999, 103, 2975 CrossRef CAS.
- B. M. Bell, W. L. Avery and A. P. Feldman, Astrophys. J., 1993, 417, L37 CrossRef CAS.
- J. D. Peeso, W. D. Ewing and T. T. Curis, Chem. Phys. Lett., 1990, 166, 307 CrossRef.
- S. Yamamoto, S. Saito, K. Kavaguch, N. Kaifu, H. Suzuki and M. Ohishi, J. Astrophys., 1987, 317, L119 Search PubMed.
- R. J. Flores, E. Martinez-Nunez, A. S. Vazquez and F. Gomez, J. Phys. Chem. A, 2002, 106, 8811 CrossRef.
- P. G. Wenthold, J. Hu and R. R. Squires, J. Am. Chem. Soc., 1994, 116, 6961 CrossRef CAS.
- J. L. Holmes, Org. Mass Spectrom., 1985, 20, 169 CAS.
- C. Wesdemiotis and F. W. McLafferty, Chem. Rev., 1987, 87, 485 CrossRef CAS.
- D. V. Zagorevskii and J. L. Holmes, Mass Spectrom. Rev., 1994, 13, 133 CAS; N. Goldberg and H. Schwarz, Acc. Chem. Res., 1994, 27, 347 CrossRef CAS.
- For NR nomenclature, see C. A. Schalley, G. Hornung, D. Schröder and H. Schwarz, Int. J. Mass Spectrom. Ion Processes, 1998, 172, 181 Search PubMed; D. V. Zagorevskii and J. L. Holmes, Mass Spectrom. Rev., 1999, 18, 87 CrossRef.
- J. H. Bowie and T. Blumenthal, J. Am. Chem. Soc., 1975, 97, 2959 CrossRef CAS; J. E. Szulejko, J. H. Bowie, I. Howe and J. H. Beynon, Int. J. Mass Spectrom. Ion Phys., 1980, 34, 99 CrossRef CAS.
- M. M. Bursey, Mass Spectrom. Rev., 1990, 9, 555 CAS.
- K. J. H. Knuithof, R. F. Schmitz and G. W. Klumpp, Tetrahedron, 1983, 39, 3073 CrossRef CAS; M. Journet, D. Cai, L. M. DiMichele and R. D. Larsen, Tetrahedron Lett., 1998, 39, 6429 CrossRef.
- A. Degl'Innocenti, A. Capperucci, P. Scafato, T. Mecca, A. Mordini and G. Reginato, Phosphorus, Sulfur Silicon, 1999, 153/154, 321.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stevens, F. J. Devlin, C. F. Chablowski and M. J. Frische, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS; D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS; T. H. Dunning, K. A. Peterson and D. E. Woon, Basis Sets: Correlation Consistent, in Encyclopedia of Computational Chemistry: P. v R. Schleyer, Ed; Wiley: Chichester, 1998 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennuchi, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Pedersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. Stefanov, G. Liu, M. A. Al-Latam, C. Y. Peng, A. Nanayakkara, M. Chalacombe, P. M. W. Gill, B. Johnson, W. Chem, M. W. Wong, J. L. Andres, C. Gonzales, M. Head-Gordon, E. S. Replogle, J. A. Pople, Gaussian 98; Revision A.9 ed.; Gaussian Inc., Pittsburgh, PA, 1998 Search PubMed.
- S. J. Blanksby, S. Dua and J. H. Bowie, J. Phys. Chem., 1999, 103, 5161 Search PubMed . To cite a particular example, the value of adiabatic electron affinity of CCCC was calculated to be 3.65 eV at the same level of theory used in this study, while the experimental value is 3.88 eV2.
- S. Lee, Chem. Phys. Lett., 1997, 268, 69 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2004 |