Hirshfeld surface analysis
Mark A.
Spackman
* and
Dylan
Jayatilaka
Chemistry - M313, School of Biomedical, Biomolecular & Chemical Sciences, University of Western Australia, Crawley, WA, Australia. E-mail: mark.spackman@uwa.edu.au; Fax: +61 8 6488 1005; Tel: +61 8 6488 3140
First published on 21st November 2008
Abstract
In the last few years the analysis of molecular crystal structures using tools based on Hirshfeld surfaces has rapidly gained in popularity. This approach represents an attempt to venture beyond the current paradigm—internuclear distances and angles, crystal packing diagrams with molecules represented via various models, and the identification of close contacts deemed to be important—and to view molecules as “organic wholes”, thereby fundamentally altering the discussion of intermolecular interactions through an unbiased identification of all close contacts.
 Mark A. Spackman Mark A. Spackman | Mark Spackman graduated from the University of Western Australia (UWA) in 1980, and after postdoctoral studies with R. F. Stewart, E. N. Maslen and B. M. Craven he joined the University of New England (1987). Recipient of an Australian Professorial Fellowship (2004–2008) from the Australian Research Council, he joined UWA in 2004. He has served as President of the Society of Crystallographers in Australia & New Zealand, and as IUCr Commission Chair on Charge, Spin & Momentum Densities. His research is the use of tools and methods from computational chemistry to inform aspects of modern crystallography, especially intermolecular interactions and crystal packing. |
 Dylan Jayatilaka Dylan Jayatilaka | Dylan Jayatilaka's interests lie in the general interaction between quantum chemistry and crystallography. He received his BSc from UWA and a PhD working with N. C. Handy at Cambridge University in 1991. After postdoctoral research with T. J. Lee at NASA Ames Research Center he returned to work with B. N. Figgis at UWA in 1993. Since then, he has been a Queen Elizabeth II Research Fellow (1996–2000), a CNRS invited researcher (2004–2005) and an Australian Research Council Senior Research Fellow (2001–2007) during which time his interests have turned to the possibility of extracting “experimental” wavefunctions from X-ray diffraction data. |
Introduction
The major themes of modern crystal engineering can all be found in Desiraju's 1989 monograph on the subject: Crystal Engineering—The Design of Organic Solids.1 That definitive work aimed to bring together organic chemists, materials scientists, physical and theoretical chemists and crystallographers and, among other things, it set out the rationale for designing crystal structures of organic molecules, summarised computational methods and databases with a view to crystal structure prediction, reviewed dominant intermolecular interactions and touched on polymorphism. It also provided the now standard definition of the topic: “the understanding of intermolecular interactions in the context of crystal packing and in the utilisation of such understanding in the design of new solids with desired physical and chemical properties”.1 However this definition begs two important questions: (i) By what means can we achieve the required understanding? and (ii) In what ways can we exploit that understanding? This Highlight focuses on a novel way of addressing the first of these questions.Aakeröy and Beatty in a recent review2 noted that “predicting and controlling the competition between intermolecular forces such as weak and strong hydrogen bonds, halogen-halogen interactions, π⋯ π contacts, van der Waals forces, etc., are part of every crystal engineering effort. The challenge comes down to the following: how do we unravel the bundle of often inter-related interactions and identify strong, directional, reliable non-covalent interactions?”
This brings us to the concept of a toolkit for crystal engineering, first discussed in 1999 by Seddon who identified synthetic vectors (hydrogen bonding, inter-ring interactions, covalent bonds, Coulombic forces), computational chemistry, visualization tools, and the Cambridge Structural Database (CSD) as the tools available at that time.3 Although the four basic types of tools remain essentially unchanged, the capabilities of computational chemistry and visualization have been greatly enhanced in the ensuing decade. There are a small number of key intermolecular interactions, as well as many others that will also be significant. How can we rationalize even the known crystal structures in terms of these interactions in order to make useful predictions? The magnitude of the problem is considerable, as there is a vast number of known organic molecular crystal structures (∼436![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in the CSD4 at January 1 2008).
000 in the CSD4 at January 1 2008).
In order to be most successful, and with the least bias possible, a method must satisfy the needs outlined by Desiraju in 1997![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 “Another compelling need is to be able to visualise a crystal structure in its entirety, not just look at selected intermolecular interactions that have been deemed to be important…”. A successful approach might also be able to address specific questions, such as those raised by Nangia and Desiraju
5 “Another compelling need is to be able to visualise a crystal structure in its entirety, not just look at selected intermolecular interactions that have been deemed to be important…”. A successful approach might also be able to address specific questions, such as those raised by Nangia and Desiraju![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 “A detailed understanding of crystal packing and crystal design depends very substantially on viewing the molecule as an organic whole. …. Given such realities, an immediate need in crystal engineering is to be able to compare crystal structures. Many will appreciate that the structure of, say, naphthalene resembles that of anthracene more than it resembles benzene. Is it possible to quantify such comparisons? If so, such quantification would amount to pattern matching and becomes important because crystals that are structurally similar are also likely to have similar properties.”
6 “A detailed understanding of crystal packing and crystal design depends very substantially on viewing the molecule as an organic whole. …. Given such realities, an immediate need in crystal engineering is to be able to compare crystal structures. Many will appreciate that the structure of, say, naphthalene resembles that of anthracene more than it resembles benzene. Is it possible to quantify such comparisons? If so, such quantification would amount to pattern matching and becomes important because crystals that are structurally similar are also likely to have similar properties.”
In the process of asking questions about ways of defining a molecule in a crystal, we stumbled on a molecular surface with rather remarkable properties. Although our original interest was in using these surfaces to compute dipole and quadrupole moments of molecules in crystals, it was immediately apparent that they had the potential to make an entirely novel contribution towards answering the sorts of questions outlined above. The paper in which we introduced the Hirshfeld surface7 noted that “The new scheme is simple to apply, aesthetically appealing, and offers some promise in routine partitioning of crystalline electron densities or in computer graphics to provide additional insight into molecular packing in crystals”. The realization of this promise has taken a considerable time, and the various steps along the way have been fully documented in the literature. This Highlight aims to complement rather than review the work already published, both our own and that of others. We will provide additional background to some of the basic tools and approaches that we have developed so far, and illustrate their application to the polymorphic molecular system 2-chloro-4-nitrobenzoic acid (2c4n), very recently described in the literature.8 The emphasis will be on providing examples to demonstrate the ways in which the various tools may be exploited, rather than on a detailed analysis of the crystal packing in the two crystalline forms.
What is the Hirshfeld surface?
The Hirshfeld surface emerged from an attempt to define the space occupied by a molecule in a crystal for the purpose of partitioning the crystal electron density into molecular fragments.7 At the time we of course knew that Bader's quantum theory of atoms in molecules (QTAM)9 provided a well-defined solution to this problem, but the zero-flux boundary surfaces are piecewise smooth, with abrupt discontinuities which make numerical integration far from trivial. We also explored a partitioning based on a generalization of the Wigner-Seitz cell, but these surfaces consisted of a union of planar or hyperbolic sections with odd irregularities. As a part of this work we quite literally stumbled on Hirshfeld surfaces, and realized that they possessed a number of attributes that make them highly attractive for an exploration of intermolecular interactions in crystals.Hirshfeld surfaces were named after F.L Hirshfeld, whose “stockholder partitioning” scheme for defining atoms in molecules suggested to us an extension to defining a molecule in a crystal. Hirshfeld's original article on that partitioning10 has attracted nearly 800 citations to date, more than 75% of them in the last five years. The majority of this recent work exploits the definition of an atomic fragment in a molecule, and hence atomic charges and other properties obtained by numerical integration. Hirshfeld defined a weight function for each atom in a molecule,
 | (1) |
| ρa(r) = wa(r)ρmol(r) | (2) |
In analogy with Hirshfeld's idea, a weight function can be defined for a molecule in a crystal,
 | (3) |
Fig. 1a illustrates contours of wA(r) surrounding a benzene molecule in the crystal. The contours are closely spaced and surround the molecule in the vicinity of the van der Waals surface. Thus the weight function is extremely flat across the molecule itself, with wA(r) > 0.9, decaying rapidly to values less than 0.1. This behaviour underpinned our decision to examine isosurfaces of wA(r), and it turned out that the isosurface defined by wA(r) = 0.5 was rather special. This isosurface—the Hirshfeld surface—envelops the molecule, and defines the volume of space where the promolecule electron density exceeds that from all neighbouring molecules. It guarantees maximum proximity of neighbouring molecular volumes, but the volumes never overlap because of the nature of the weight function. The Hirshfeld surface for benzene is visualized in Fig. 1b, at the same size and orientation as the 0.5 contour in Fig. 1a, and surrounded by the 12 nearest neighbour molecules in the crystal. Practical details regarding the computation of the Hirshfeld surface have been reported elsewhere,12,13 and the suite of tools for Hirshfeld surface analysis described in this Highlight are available in CrystalExplorer 2.1.14
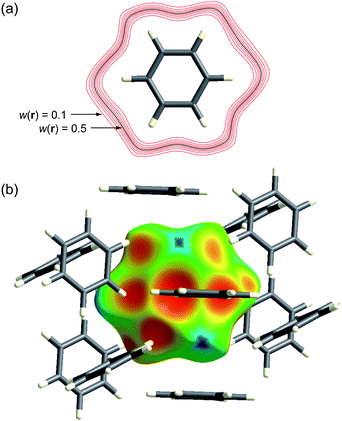 | ||
| Fig. 1 (a) Contours of wA(r) surrounding a benzene molecule in the crystal; (b) the Hirshfeld surface for benzene mapped with de (Table 1) plotted at the same size and orientation as the 0.5 (black) contour in (a). | ||
How does the Hirshfeld surface differ from other molecular surfaces?
Chemists regularly use molecular surfaces in efforts to visualize and quantify the sizes and shapes of molecules, and we have previously discussed in detail a number of the most common definitions and their relative merits.15 These range from the common fused sphere van der Waals (or CPK) and smoothed Connolly surfaces, both of which rely on defining a set of appropriate atomic radii, to isosurfaces defined by either the promolecular or molecular electron distribution. In ref. 15 we compared volumes and surface areas of CPK and promolecular surfaces with those obtained from an ab initio electron density, and concluded that the promolecular surface, with contracted hydrogen atoms, provides results that are remarkably consistent with ab initio values. The use of a contracted hydrogen atom electron density (i.e. with an orbital exponent of 1.24 au, rather than 1.00 au for the isolated atom) is essential for this purpose, and it reflects the known contraction of hydrogen upon chemical bonding.16 The same definition of the promolecule is used by us in computing Hirshfeld surfaces viaeqn (3).Fig. 2 compares the Hirshfeld surface for the molecule in form I of 2c4n with a fused sphere representation and with the 0.002 au isosurface of the ab initio electron density. As observed earlier for naphthalene and terephthalic acid,17 the Hirshfeld surface generally encloses both CPK and 0.002 au electron density isosurfaces, except where atoms make close contacts with neighbouring molecules. This is especially noticeable for the carboxyl O and H atoms, which participate in a cyclic hydrogen bonded dimer (see below), but there are many other atoms for which the CPK or electron density surfaces protrude beyond the Hirshfeld surface. Together, these figures highlight the fact that although the Hirshfeld surface defines a volume around a molecule in a manner similar to a van der Waals surface, or an outer surface of the electron density, it is completely different from those surfaces. These other molecular surfaces are defined only by the molecule itself, whereas the Hirshfeld surface is defined by the molecule and the proximity of its nearest neighbours, and hence encodes information about intermolecular interactions.
 | ||
| Fig. 2 (a) Comparison between CPK (vdW radii of 1.20, 1.70, 1.55, 1.50 and 1.75 Å for H, C, N, O and Cl) and Hirshfeld surfaces (grey, transparent) for a molecule of 2-chloro-4-nitrobenzoic acid (form I); (b) comparison between the Hirshfeld surface (mapped with dnorm, Table 1) and the 0.002 au isosurface of the HF/Midi! electron density. | ||
This is the key attribute of relevance to the analysis of molecular crystal structures, but it needs to be recognised that this comparative advantage comes with a caveat: the crystal structure needs to be well-characterised. By this we mean that all hydrogen atoms need to be located accurately, as do the location and identity of solvent molecules, and any disorder present needs to be modelled and information about disorder groups included in the CIF file. Furthermore, in order to make meaningful comparisons between crystal structures it is essential that bond distances to H atoms are standardised to realistic values. For this purpose CrystalExplorer uses average bond distances derived from neutron diffraction experiments,18 and a value of 1.190 Å for B–H (see ref. 19).
In the following sections we will provide many examples of functions mapped on Hirshfeld surfaces for two polymorphs of 2c4n crystallizing in space groupP21/c. We have chosen this system because the recent report of room-temperature single crystal X-ray structures did not include a detailed analysis of the crystal packing in the two forms. Packing diagrams are provided in Fig. 3, and from these we see that while both forms incorporate cyclic dimers characteristic of carboxylic acids, there is one unique molecule in form I, but four molecules in the asymmetric unit of form II. Moreover, although the original report concentrated on a graph set analysis of the hydrogen bonding patterns, we will see that many more intermolecular contacts can be readily identified using Hirshfeld surface analysis.
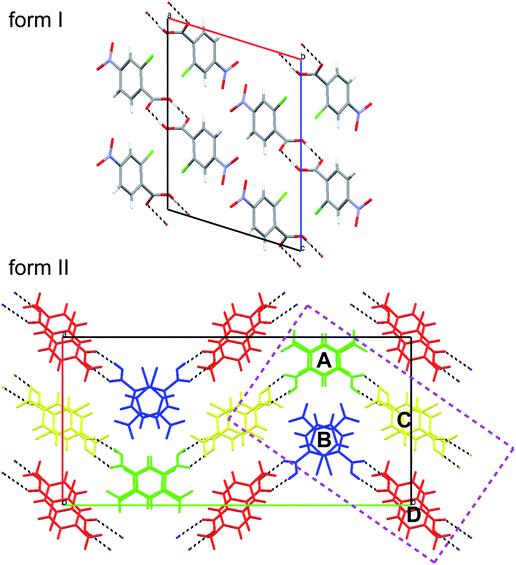 | ||
| Fig. 3 Mercury 20 packing diagrams for forms I and II of 2-chloro-4-nitrobenzoic acid. The four molecules in the asymmetric unit of form II are coloured and labelled in a manner consistent with the original publication.8 The rectangular region bounded by dashed purple lines delineates the subset of four molecules extracted from the cell and used for illustrative purposes. | ||
Properties of the Hirshfeld surface: volume, surface area and functions of curvature
In one of our earliest publications on Hirshfeld surfaces we concluded that quantities derived directly from the surfaces, including their volume, VH, surface area, SH, and packing ratio, PH = ∑VH/Vcell, were not particularly informative.12 This follows from the definition of the weight function, which guarantees that any empty space in the crystal, either interstices between molecules or genuine vacancies due to unidentified solvent, will be effectively subsumed by the surface. At first sight this seems counterintuitive, but it can be exploited to advantage, as recently shown dramatically for molecules in form II of carbamazepine, where the molecular Hirshfeld surfaces are greatly extended in the direction of channels running down the threefold axis.21 This behaviour was anomalous in comparison with many hundreds of other molecular crystals, and was shown to result from the omission of disordered solvent molecules in the crystal structure. In other words, anomalous features of Hirshfeld surfaces can be used to readily pinpoint anomalies in crystal structures.One of our first attempts to decode the information on intermolecular contacts embodied in Hirshfeld surfaces focused on the local shape of the surfaces themselves. Curvature is an intrinsic property of any surface, and it has been shown to play an important role in many areas of condensed matter biology, chemistry and physics.22 For this purpose we found the two functions of curvature introduced by Koenderink to convey far more information than the usual mean and Gaussian curvatures. Based on the two local principal curvatures, κ1 and κ2, computed numerically at each point of the triangulated surfaces, shape index and curvedness are computed according to Table 1. Shape index has the very useful property that two shapes that differ by only a change of sign represent complementary pairs, and because of this maps of shape index on the Hirshfeld surface can be used to identify complementary hollows (red) and bumps (blue) where two molecular surfaces touch one another. Curvedness is a function of the root-mean-square curvature of the surface, and maps of curvedness typically show large regions of green (relatively flat) separated by dark blue edges (large positive curvature).
| Function | Symbol and definition | Mapping range |
|---|---|---|
| distance from a point on the surface to the nearest nucleusoutside the surface | d e | red (short distances) through green to blue (long distances) |
| distance from a point on the surface to the nearest nucleusinside the surface | d i | red (short distances) through green to blue (long distances) |
| shape index, S, a measure of “which” shape, defined in terms of principal curvatures κ1 and κ2 |

|
−1.0 (concave) through 0.0 (minimal surface) to +1.0 (convex) |
| curvedness, C, a measure of “how much” shape,, defined in terms of principal curvatures κ1 and κ2 |
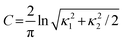
|
−4.0 (flat) through 0.0 (unit sphere) to +0.4 (singular) |
| normalized contact distance, defined in terms of de, di and the vdW radii of the atoms |
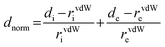
|
red (distances shorter than sum of vdW radii) through white to blue (distances longer than sum of vdW radii) |
Fig. 4 and 5 illustrate how shape index and curvedness can be used to identify characteristic packing modes, in particular planar stacking arrangements, and even the ways in which adjacent molecules contact one another. For example, the shape index surface in Fig. 4 clearly shows that the two sides of the molecule are involved in quite different contacts with neighbouring molecules and, because the curvedness plots show no flat surface patches above either side of the benzene ring, there is no evidence of planar stacking between molecules in form I. The situation in form II is completely different (Fig. 5). Here the curvedness surfaces show broad, relatively flat regions characteristic of planar stacking of molecules. Furthermore, distinctive features can be identified on the shape index plots which can be used to analyse the ways in which the various molecules pack against themselves. The yellow ellipses in Fig. 5 outline self-complementary regions: there is another identical molecule above each, related by an inversion centre. These patches are only seen on the surfaces of molecules C and D, which form stacks of molecules related by centres of symmetry along the c axis (Fig. 3). But these plots contain still more information about these stacks. From the front and back views of the cluster in Fig. 5 it is obvious that the two sides of molecules C and D are different, a consequence of the fact that there are two different centres of symmetry alternating along the c axis for each stack. Complementary patches for molecule A are outlined by two white rectangles in Fig. 5, and those for molecule B by two magenta rectangles. The observant reader will recognize that the complementary red and blue triangles of either pair cannot be brought together by any combination of proper rotations and translations. Instead, they require an improper rotation, a consequence of the fact that in space groups incorporating an improper rotation (e.g. mirror plane, glide plane or inversion centre) each molecule in the unit cell has a partner related by that operation, and their Hirshfeld surfaces will not be superimposable unless the molecules themselves incorporate the improper symmetry element. These patterns of triangles on the shape index surface are diagnostic for close C⋯C interplanar contacts,13 and because of this the presence - or absence - of this packing motif in a crystal structure is readily identifiable by mapping this property, especially in conjunction with a breakdown of the fingerprint plot (see below).
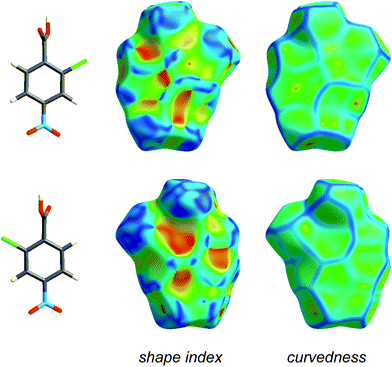 | ||
| Fig. 4 Front and back views of the Hirshfeld surface for form I of 2-chloro-4-nitrobenzoic acid, mapped with shape index and curvedness (Table 1). | ||
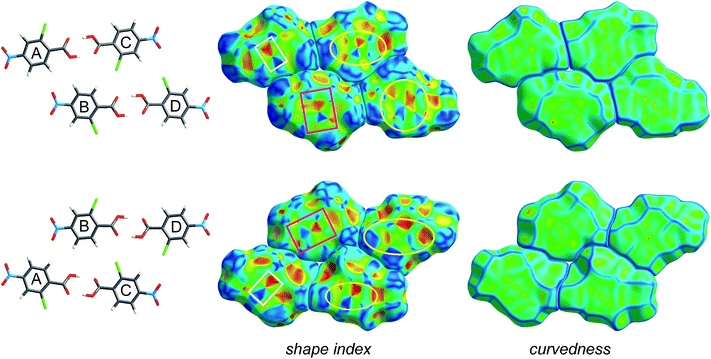 | ||
| Fig. 5 Hirshfeld surfaces for a cluster of four molecules in form II of 2-chloro-4-nitrobenzoic acid, mapped with shape index and curvedness (Table 1). The two rows represent front and back views of the same group of molecules outlined in purple in Fig. 3, namely the hydrogen bonded dimers A⋯C and B⋯D. Highlighted regions on the shape index surface indicate complementary patches (i.e. white rectangles with one another, magenta rectangles with one another; yellow ellipses are self-complementary). | ||
Functions of distance: de, di, dnorm and fingerprint plots
Distances from the Hirshfeld surface to the nearest nucleus inside the surface (or internal, di) and outside the surface (or external, de) were the first functions of distance explored for mapping on the surfaces (Table 1).23 Numerous applications of these measures to a wide range of molecular crystals were published in a Topical Review in Acta Crystallographica,13 and we will not present additional examples here—with the exception of that for benzene (Fig. 1). In recent work we—and many others—have found the combination of di and de in the form of a 2D fingerprint plot to provide a more informative use of these quantities. The fingerprint plot was invented to overcome the difficulty of representing in a 2D format (printed page or computer monitor) two different but potentially useful distance measures, each mapped on a 3D molecular surface. The resulting—and now standard—plot is created by binning (di, de) pairs in intervals of 0.01 Å and colouring each bin (essentially a pixel) of the resulting 2D histogram as a function of the fraction of surface points in that bin, ranging from blue (few points) through green to red (many points).23Fig. 6 compares fingerprint plots for the four molecules in form II of 2c4n with that for form I. These plots convincingly demonstrate an important feature of the fingerprint plots: they are highly sensitive to the immediate environment of the molecule, and indeed unique for a given molecule in a particular polymorphic form. As such, fingerprint plots have been found to be exceptionally useful in studies where comparisons are sought between different crystal structures incorporating the same molecule, for example different polymorphs24 or structures determined at elevated pressures.25Fig. 6 shows that the four molecules in form II of 2c4n are more similar to one another than they are to the single molecule in form I, despite the fact that the dominant interaction in both forms is the cyclic hydrogen bond characteristic of carboxylic acids. This interaction shows up as a pair of spikes at the bottom left of the plot (i.e. short di and de, the upper one associated with the donor atom, the lower one with the acceptor), and the pattern of diffuse points in between these spikes occurs only for cyclic hydrogen bonds.13 Participation in a planar stacking arrangement of molecules (for example, so-called π⋯ π stacking) shows up as a red region near the centre of the plot, in the vicinity of (di, de) ∼ 1.8–2.0 Å, a range typical of the interplanar spacing of polycyclic aromatic hydrocarbons. This feature is quite obvious for all molecules in form II of 2c4n, but absent for form I. A third principal interaction identifiable in Fig. 6 is due to Cl⋯H hydrogen bonds, and shows up as a pair of spikes, this time with much greater separation across the diagonal of the plot, and at much greater values of (di, de). This feature is common to all molecules in both forms of 2c4n.
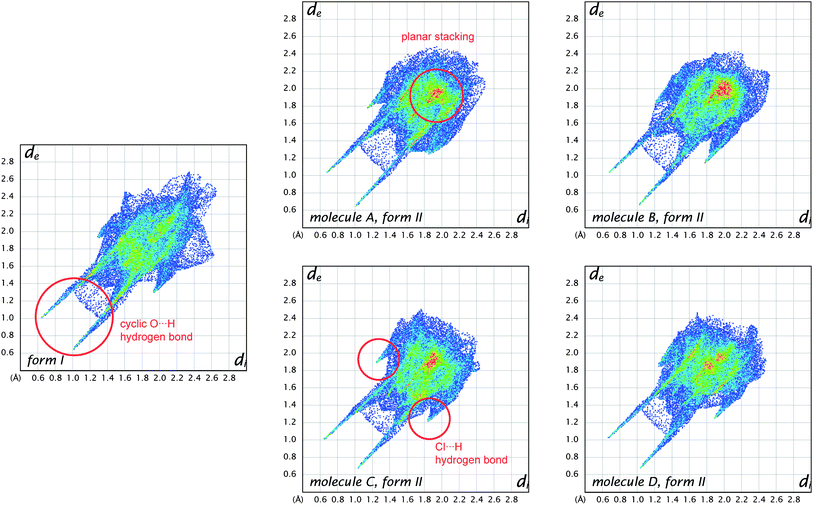 | ||
| Fig. 6 Comparison between fingerprint plot for the single molecule in form I of 2-chloro-4-nitrobenzoic acid and those for the four different molecules in form II. Features characteristic of key intermolecular contacts are circled in red. | ||
The observation that the fingerprint plots for the four molecules in form II are more similar to one another than they are to that for form I—based purely on visual inspection—suggests that it should be possible to quantify such a concept and perhaps provide an answer to the question posed by Nangia and Desiraju,6 as discussed in the Introduction. A first attempt in this direction has been described by Parkin et al., and has been termed structural genetic fingerprinting.26 It is based on a more coarse-grained version of the fingerprint plots (bin width of 0.04 Å), and a calculation of a correlation coefficient between individual plots, followed by visualisation of the correlation coefficients using dendrograms and other techniques using dSNAP.27 In that work the example given as a proof-of-concept concerned the similarities between crystal structures of twelve polycyclic aromatic hydrocarbons, and it quite convincingly demonstrated that it is possible to not only confirm the expectation that naphthalene is more similar to anthracene than to benzene, but to quantify the degree of similarity. The method is quite general, and is expected to be applied to a greater number of systems in the future.
One of the reasons that we have not discussed maps of either di or de at length in this Highlight is that these distances fail to take into account the differing sizes of atoms. This is not a problem for computing and interpreting fingerprint plots, and in fact it is an advantage because it spreads features apart in the plots (e.g.hydrogen bonds to Cl are in quite a different region of the plot from those to O, see Fig. 6). However when de is mapped on a Hirshfeld surface, it can be difficult or impossible to highlight close contacts to large atoms like Br or I at the same time as close contacts to H, C and O. To overcome this deficiency we recently proposed a contact distance, dnorm (Table 1), that combines both de and di, each normalised by the vdW radius for the particular atoms involved in the close contact to the surface. Using a red–white–blue colouring scheme to distinguish it from the red–green–blue schemes for de and di, contacts shorter than vdW separations show up as red spots on a largely blue surface. And because the definition of dnorm is symmetric in both de and di, close intermolecular contacts appear as two identical red spots (but not necessarily on the same molecule if there is more than one molecule in the asymmetric unit). An example is given in Fig. 7 for form I of 2c4n, where we see that the short cyclic hydrogen bond between H4 and O1 is associated with two large red spots of the same size, while the longer H5⋯O3 contact (also cyclic) shows up as an identical pair of much smaller red spots on the surface. The still longer H6⋯O4 contact is characterised by two slightly smaller red spots, one at the top of the figure and one at the bottom. The only other faint red spot visible on the dnorm surface in Fig. 7 is associated with a Cl⋯O2 contact of 3.16 Å, slightly shorter than the vdW separation of 3.27 Å (for clarity the other molecule is not shown in the figure). The dnorm surface has proven to be extremely useful as an unbiased means of identifying all close contacts in quite complex crystal structures, as exemplified by recent studies on inclusion complexes of p-H-calix[5]arene28 and cholamide.29
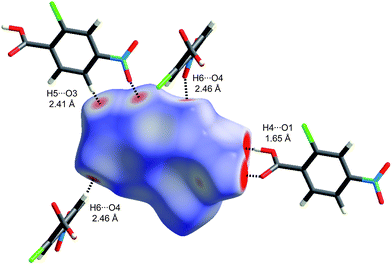 | ||
| Fig. 7 Hirshfeld surface for form I of 2-chloro-4-nitrobenzoic acid mapped with dnorm (Table 1) over the range −0.4 to 1.4. Neighbouring molecules associated with close contacts are shown along with distances between the atoms involved. | ||
Breaking down the Hirshfeld surface
It can be seen from the definition of dnorm (Table 1) that its computation at each point on the triangulated Hirshfeld surface requires identification of the atom types associated with the distances de and di. This means that it is relatively trivial to break down the surface into patches associated with specific atom-type/atom-type pairs, to highlight just those regions on the surface, and even sum the areas of surface patches associated with various contacts and construct a histogram of relative areas for comparing molecules in different environments. Histograms of this kind have been reported in comparisons between benzene, naphthalene and anthracene and two forms of paracetamol,30 as well as three polymorphic forms of 3-methyl-4-methoxy-4′-nitrostilbene (MMONS).31The present example of 2c4n provides us with five different molecular environments for comparison, and the resulting histogram is reproduced in Fig. 8. From this comparison it is readily seen that for all five molecules hydrogen bonding interactions are associated with nearly 50% of the surface area, and of these (and unsurprisingly) O⋯H contacts dominate. Although Cl⋯H contacts are apparent in both forms, in form II they occupy around twice the surface area of those in form I. Perhaps surprisingly, around 10% of all molecular surfaces is associated with relatively close Cl⋯O contacts (see also Fig. 7), an observation that we believe would not have been possible without performing an analysis of this kind, and we explore the nature of this contact in the following section. A final observation deriving from Fig. 8 concerns the relative areas associated with C⋯C contacts (often referred to as π⋯ π contacts) and associated with the planar stacking arrangement in form II. In fact from Fig. 8 we see that slightly less than 10% of the surface can be identified as C⋯C for all molecules in form II, but there is a negligible amount (actually 0.4%) in form I. These numbers very nicely support the obervations based on fingerprint plots in Fig. 6.
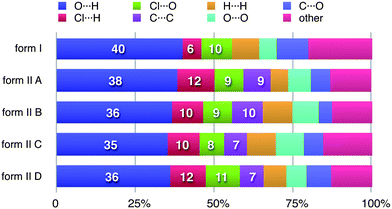 | ||
| Fig. 8 Percentage contributions to the Hirshfeld surface area for the various close intermolecular contacts for molecules in forms I and II of 2-chloro-4-nitrobenzoic acid. Percentages are given on the histogram only for the major atom-type/atom-type contacts discussed in detail in the text. | ||
Other properties mapped on the Hirshfeld surface
In the paper introducing the Hirshfeld surface we remarked that “It should prove extremely interesting to encode a property such as electrostatic potential on these surfaces”.7 This is indeed the case, as shown by our first attempts of this kind, applied to a series of small cyclic molecules crystallizing in space groupsP41212 or P43212.32 In that work we exploited a new feature of CrystalExplorer to utilize Gaussian0333 to compute ab initio wavefunctions for molecules at the same geometry and orientation as used internally by CrystalExplorer, and then use the Gaussian checkpoint file to produce maps of the ab initio electrostatic potential on either an isosurface of the electron density or the Hirshfeld surface.† This approach convincingly demonstrated the sort of insight that can be obtained almost immediately by the display of a property such as the electrostatic potential of a molecule within a crystal packing diagram. In particular, that work provided very strong evidence that the concept of “electrostatic complementarity”, commonly discussed in the context of protein structure and binding,34 is also a guiding principle in a variety of intermolecular contacts in crystals. A further example of the usefulness of this approach is given in Fig. 9, which compares Hirshfeld surfaces mapped with HF/Midi! electrostatic potentials for all five molecules in the two forms of 2c4n.‡ We present these maps in isolation because they illustrate, in a rather dramatic fashion, how the electrostatic potential for this simple molecule varies strongly with the rotation of the carboxyl group relative to the phenyl ring. The molecules in the figure are arranged from left to right in order of increasing torsion angle of the –COOH group relative to the benzene ring, with a reference angle of 0° corresponding to a coplanar arrangement with the carbonyl oxygen adjacent to the Cl atom.§ A number of observations are readily made upon inspection of these plots. The most obvious is that the electronegative region around the carboxyl group extends to the chlorine atom when the two are close (molecules A and C in form II), and as the carboxyl group rotates away from the chlorine atom the region around the Cl becomes much less electronegative (form I) and eventually (molecules B and D in form II) the electronegative region near the carbonyl oxygen separates from that near the Cl atom, which in turn shows only a slight electronegative character. This trend in electrostatic nature of the molecules is also reflected in the dipole moments. Thus we see that the two hydrogen-bonded dimers in form II comprise two different pairs of molecules: in the A⋯C dimer both molecules have the carbonyl oxygen close to the chlorine, and a dipole moment near 4.5 D, whereas the B⋯D dimer has the carbonyl oxygen of both molecules away from the chlorine, with much smaller dipole moments of 3.4 D. This difference in turn must influence the ways in which the two dimers can be arranged in the crystal, but we will not discuss that aspect any further in this Highlight.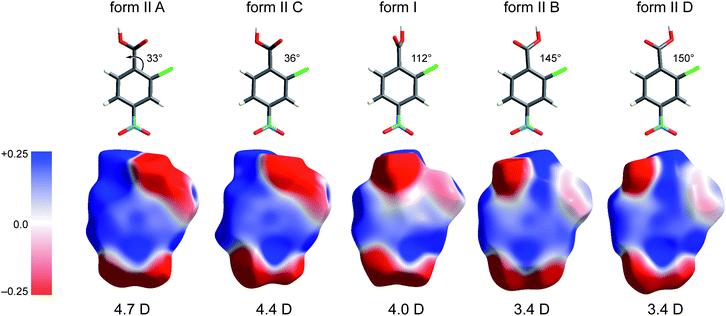 | ||
| Fig. 9 Electrostatic potentials mapped on Hirshfeld surfaces for molecules in forms I and II of 2-chloro-4-nitrobenzoic acid. The potential is mapped over the range ±0.025 au, and molecules are arranged in order of increasing torsion angle of the –COOH group relative to the plane of the benzene ring. HF/Midi! dipole moments are given below the molecules, and these decrease with increasing rotation of the –COOH group. | ||
As a final example for this Highlight, Fig. 10 shows how the breakdown of the fingerprint plot can be used to identify the patterns associated with specific interactions (O⋯H, Cl⋯H, etc.). However, more chemical insight can be obtained by mapping just those surface patches that contribute to particular patterns, and in Fig. 10 the electrostatic potential is used to illustrate the possibilities offered by this tool. We see that for O⋯H and Cl⋯H contacts there are clearly identifiable electropositive (blue) and electronegative (red) regions that are complementary. For example, the carboxyl region has a red and a blue patch, associated with acceptor (O1) and donor (H4) atoms, respectively. Similarly, the electropositive region near H3 (between the Cl and nitro groups) is complementary to the electronegative region on the surface at the sides of the Cl atom. This electrostatic complementarity is even evident for the Cl⋯O contact, which consists primarily of an electronegative patch near O4 of the nitro group and the electropositive region beyond the Cl atom. The planar stacking contact consists largely of C⋯C contacts, and from Fig. 10 we see that these are slightly electropositive everywhere, a sign that this contact cannot be considered to be strongly electrostatic.
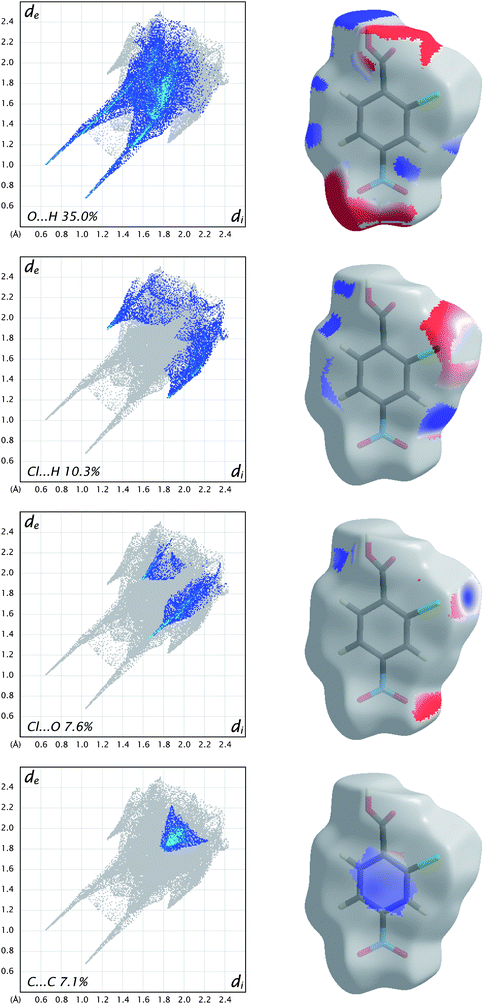 | ||
| Fig. 10 Fingerprint plots for molecule C in form II of 2-chloro-4-nitrobenzoic acid, broken down into contributions from specific pairs of atom-types. For each plot the grey shadow is an outline of the complete fingerprint plot (see Fig. 6). Surfaces to the right highlight the relevant surface patches associated with the specific contacts, with the electrostatic potential mapped in the same manner as Fig. 9. | ||
Some finer points: disorder, metal atoms and charged species
No method of analysis such as this can be without limitations, and we have already encountered a major one: the crystal structure needs to be well-determined and in particular hydrogen atoms must be located and solvent modelled accurately. This of course reflects the fact that the Hirshfeld surface for a molecule is defined by the proximity and identity of atoms in neighbouring molecules, hence an incorrect or ill-defined structure will yield meaningless results. The requirement that all hydrogen atoms be located accurately is an obvious one, as hydrogen atoms are typically at the periphery of a molecule, and errors in their positions - or their omission - will produce artifacts in the results, especially the fingerprint plots. It also means that application of these tools to protein structures is unlikely to happen in a routine fashion. However, this can also be exploited by using anomalies in fingerprint plots to identify errors or physically unrealistic close contacts in structures.This requirement would also seem to preclude application of the technique to crystals exhibiting disorder, but that is not necessarily the case, as we have shown recently in the analysis of three polymorphs of 3-methyl-4-methoxy-4′-nitrostilbene (MMONS).31 One of the polymorphs has Z′ = 2, with one site ordered and the other occupied by two different conformers. Because the disorder could be modelled with some confidence a Hirshfeld surface analysis was performed on each of the possible ordered structures, in each case assuming a site occupancy of atoms in the disordered molecule of 1.0 (i.e. the _atom_site_occupancy in the CIF file must be edited manually). An alternative approach would involve defining the Hirshfeld surface of the relevant molecule by incorporating fractional occupancies of the disordered atoms (information that must be included in the CIF file), which amounts to using a weighted average representation of the promolecule electron density. This approach was successfully applied to the analysis of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of C70 with p-benzylcalix[5]arene, where the C70 molecule is disordered over two orientations.35
1 complex of C70 with p-benzylcalix[5]arene, where the C70 molecule is disordered over two orientations.35
Although our own research has so far concentrated on organic molecular crystals, Hirshfeld surface analysis need not be limited to those systems. However, application to metal-organic and/or ionic molecular systems requires a little more thought for a number of reasons. The current version of CrystalExplorer is limited to treating atoms up to and including Xe. Therefore, metal-organic crystals incorporating the first two rows of transition metals cause no problems (a recent example is the inclusion complex between C60 and a saddle-shaped Ni macrocycle36), but complexes including Pt or Au, for example, cannot be studied at present. This will be overcome in the near future by replacing the present Hartree–Fock atomic electron densities with a relativistic set for atoms up to Z = 103. Until that time it is still possible to obtain useful information from Hirshfeld surface analysis by recognising that the Hirshfeld surface is only a device by which intermolecular interactions can be highlighted and, furthermore, the precise nature of the electron density of a metal atom inside a cluster of ligands will play a very small part in determining the surface of the complex. This suggests that substituting Pt or Au atoms in the CIF file by Pd or Ag atoms, respectively, is a viable approach, especially if comparison is sought between two or more related complexes (e.g. subtle change of ligand or halogen atom).
At first sight the definition of the weight function, eqn (3), in terms of spherical atomic (i.e. neutral) electron densities would seem to preclude meaningful application to crystals containing charged species. Again, because the Hirshfeld surface partitions space as a means to an end, the use of neutral atomic electron densities to define a surface around an ion is not a contradiction, and Hirshfeld surface analysis can be successfully applied to such systems without modification. This does not mean that a different definition of the weight function, for example using ionic electron densities, will yield the same results. To demonstrate this for Na and Cl in the NaCl rocksalt structure Fig. 11 compares the 0.5 isosurface of the atomic weight function, Fig. 11a, with that obtained using ionic electron densities, Fig. 11b. Both are compared with zero-flux QTAM surfaces in Fig. 11c. Dramatic differences occur changing from neutral atom to ionic electron densities, in most part due to the large difference in behaviour of the Na electron density compared with that for Na+ (the outer 3s electron of Na is very diffuse, resulting in an atomic electron density that decays much more slowly than that for the ion). Quite remarkably, the use of ionic electron densities to define the Hirshfeld weight function results in surfaces that more closely resemble zero-flux surfaces obtained by Bader's QTAM partitioning. This has previously been noted by Pendas et al.,38 and deserves closer attention.
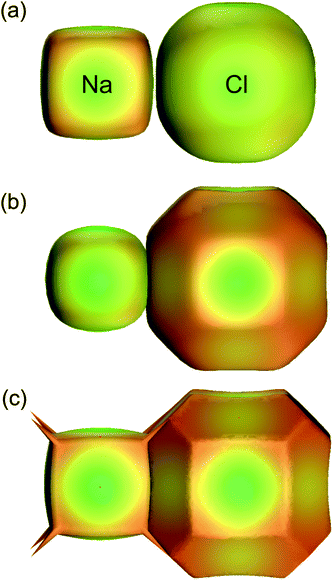 | ||
| Fig. 11 For Na and Cl in the NaCl rocksalt structure, 0.5 isosurfaces of the weight function, eqn (3), using (a) neutral atomic electron densities (i.e. Hirshfeld surfaces) and (b) ionic electron densities. The QTAM zero-flux surfaces from a crystal Hartree–Fock calculation are depicted in (c). For all surfaces the colour maps electron density on the surface, and is only intended as a visual aid (adapted from ref. 37). | ||
Future directions
Hirshfeld surface analysis represents a radical—and visually appealing—new approach to the investigation of the interactions between molecules in crystals. Prior to this research the analysis of the interactions between molecules in crystals focused almost entirely on a discussion of specific internuclear distances and angles, crystal packing diagrams with molecules represented via ball-and-stick or stick models, and the identification of close contacts between atoms in neighbouring molecules that were deemed to be indicative of important interactions. Our collaborative research over the last few years, especially the publications and the embodiment of all original ideas and tools in CrystalExplorer, constitutes an attempt to venture beyond this paradigm, and to view molecules as “organic wholes”, thereby fundamentally altering the discussion of intermolecular interactions through an unbiased picture of all close contacts. The synergistic relationship developed between high-level programming and graphics, quantum chemistry, and crystal engineering represents a rare (perhaps even a unique) approach. Although the bulk of this research has been published only in the last three years, and CrystalExplorer has been freely available for less than two years, it is already clear from the number of third-party publications that this is rapidly becoming adopted as an important new approach to the analysis of crystal packing and intermolecular interactions in crystals.Our future focus with respect to Hirshfeld surface-based tools will be the mapping of voids and their properties in molecular crystals, as well as the investigation of a range of additional functions mapped on Hirshfeld surfaces, and derived from theoretical wavefunctions (e.g. local ionization energies, molecular orbital densities, and local electron affinities), functions which should provide information that complements that already available. The current interface of CrystalExplorer to the powerful Gaussian quantum chemistry package provides a means of opening up crystal engineering to a rigorous quantum chemical approach, and we intend to exploit this by incorporating the computation of intermolecular interaction energies into CrystalExplorer. This development will make the software powerful enough to not only routinely explore and visualize the patterns of interactions experienced by molecules in crystals, but also provide meaningful energies of interaction between relevant pairs of molecules. In this way researchers will be able to readily attach some real significance—energetics—to what has hitherto been simply a close contact, and for that reason assumed to be strongly attractive.
Hirshfeld surfaces mapped in colour with various functions have a tremendous visual appeal, and we aim to further developments of this kind by investigating ways of capitalizing on the power of modern computer graphics and visualization tools such as movies, virtual reality and immersive graphics environments. And there is also some fun to be had in producing real tangible models of Hirshfeld surfaces—in colour—on 3D prototyping printers (Fig. 12).
 | ||
| Fig. 12 Solid models of Hirshfeld surfaces for benzene produced with a ZCorp Z510 printer. Clockwise from top left the surfaces are mapped with dnorm, shape index, de and curvedness (Table 1). | ||
Historical footnotes
In his recent review39 in Angewandte Chemie Desiraju identified two key research groups whose work can be viewed as the origins of modern crystal engineering: the solid state organic photochemistry carried out in G. M. J. Schmidt's laboratory at the Weizmann Institute over the period 1950–1970, and the more general physical chemistry of organic crystals studied by A. I. Kitaigorodsky and co-workers at the Institute of Elementoorganic Chemistry of the USSR Academy of Sciences between 1940 and 1980.It is widely reported that the modern meaning of the term crystal engineering dates to a 1971 paper by Schmidt,40 but it appears not to be well known that F. L. Hirshfeld was a PhD student of Schmidt's in the 1950s. A brief summary of Hirshfeld's contributions to crystallography does not mention this point,41 but we find it entirely appropriate that there is an important and substantial link between Hirshfeld and Schmidt. They published only six papers together, between 1954 and 1965, after which Hirshfeld made pioneering contributions to accurate X-ray diffraction studies, including thermal motion analysis and electron density determination. An exception among this body of work is a single paper42 on the importance of the electrostatic term in calculating the lattice energy of molecular crystals via an atom–atom approach, including a comparison between atomic charge and atomic multipole moment representations. Three decades on these topics are still receiving attention in the modern crystal engineering literature. This paper was co-authored by K. Mirsky who, before 1973, and as K. V. Mirskaya, published several papers with Kitaigorodsky on the atom–atom potential approach, including crystal structure prediction, between 1965 and 1972. In her recollection of the early days with Kitaigorodsky, Mirsky noted that Desiraju's 1989 monograph provided a “comprehensive discussion” of the atom–atom potential approach “with respect to the possibilities of applying it to crystal engineering (a new discipline which AIK used to contemplate a great deal…)”.43
Kitaigorodsky's enduring works are the two monographs Organic Chemical Crystallography44 and Molecular Crystals and Molecules.45 Some time ago we noticed that the packing of objects remarkably similar to Hirshfeld surfaces is depicted in Fig. 2.68 of Modern Crystallography II.46 No source was given for that figure, but it appears to have been adapted from Fig. 62 of Kitaigorodsky's Organic Chemical Crystallography, and first published in Russian in 1955. In that figure Kitaigorodsky used simplified representations of molecules to explain the way in which a 21 axis leads to close packing of molecules, although the text gives no indication of precisely what these objects represent. Fig. 13 reproduces a part of that figure, along with a Hirshfeld surface packing diagram for C2F4 (space groupP21/n). The similarity between the two is striking.
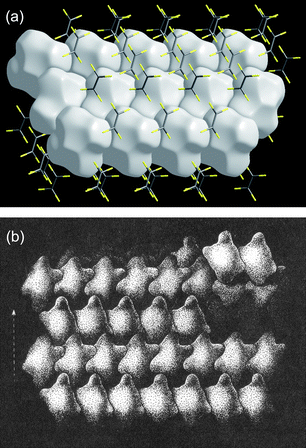 | ||
| Fig. 13 (a) Packing diagram of Hirshfeld surfaces for C2F4 (CSD refcode GAFLIJ, space groupP21/n); (b) close packing diagram, adapted from Fig. 62, p 93 of ref. 44 (with kind permission of Spinger Science and Business Media). | ||
Acknowledgements
The suite of tools known as Hirshfeld surface analysis is the result of the combined efforts of a large number of collaborators. The original idea arose at the University of New England from discussions with Patrick Byrom, and early graphical development was undertaken by Anthony Mitchell. Joshua McKinnon has been involved in the project since 1997, and his contribution to the exploration of the use of the various tools, their evolution, recent software development, web page construction and software documentation has greatly influenced the final outcome. At the University of Western Australia CrystalExplorer has grown considerably from the initial work of Steve Wolff, Daniel Grimwood and Dylan Jayatilaka, supported by a UWA Office of Industry & Innovation startup fund. Since 2004 this work has been supported by the Australian Research Council.References
- G. R. Desiraju, Crystal Engineering: The Design of Organic Solids, Elsevier, Amsterdam, 1989 Search PubMed.
- C. B. Aakeröy and A. M. Beatty, Aust. J. Chem., 2001, 54, 409–421 CrossRef CAS.
- K. R. Seddon, in Crystal Engineering. The Design and Application of Functional Solids, ed. K. R. Seddonand M. Zaworotko, Kluwer Academic, Amsterdam, 1999, pp. 1–28 Search PubMed.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef.
- G. R. Desiraju, Chem. Commun., 1997, 1475–1482 RSC.
- A. Nangia and G. R. Desiraju, in Design of Organic Solids, ed. E. Weber, Springer-Verlag, Berlin, 1998, pp. 57–95 Search PubMed.
- M. A. Spackman and P. G. Byrom, Chem. Phys. Lett., 1997, 267, 215–220 CrossRef CAS.
- I. Barsky, J. Bernstein, P. W. Stephens and K. H. Stone, New J. Chem., 2008, 32, 1747–1753 RSC.
- R. F. W. Bader, Atoms in Molecules—A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- P. Coppens, G. Moss and N. K. Hansen, in Computing in Crystallography, ed. R. Diamond, S. Ramaseshan and K. Venkatesan, Indian Academy of Sciences, Bangalore, 1980, pp. 16.01–16.18 Search PubMed; F. L. Hirshfeld and H. Hope, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 406–415 Search PubMed; G. Moss and P. Coppens, Chem. Phys. Lett., 1980, 75, 298–302 CrossRef.
- J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Chem.–Eur. J., 1998, 4, 2136–2141 CrossRef CAS.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef.
- S. K. Wolff, D. J. Grimwood, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystalExplorer 2.1, ( 2007) University of Western Australia (http://hirshfeldsurface.net/CrystalExplorer), Perth Search PubMed.
- A. S. Mitchell and M. A. Spackman, J. Comput. Chem., 2000, 21, 933–942 CrossRef CAS.
- W. J. Hehre and J. A. Pople, J. Am. Chem. Soc., 1970, 92, 2191–2197 CrossRef CAS; W. J. Hehre, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1969, 51, 2657–2664 CrossRef CAS; R. F. Stewart, E. R. Davidson and W. T. Simpson, J. Chem. Phys., 1965, 42, 3175–3187 CrossRef CAS.
- J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Chem. Commun., 1998, 2071–2072 RSC.
- F. H. Allen, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, in International Tables for Crystallography, ed. E. Prince, Springer Verlag, Berlin, 3rd edn, 2004, vol. C: Mathematical, physical and chemical tables, pp. 790–811 Search PubMed.
- M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2007, 10, 377–388 Search PubMed.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- F. P. A. Fabbiani, L. T. Byrne, J. J. McKinnon and M. A. Spackman, CrystEngComm, 2007, 9, 728–731 RSC.
- The Language of Shape, ed. S. Hyde, S. Andersson, K. Larsson, Z. Blum, T. Landh, S. Lidin and B. W. Ninham, Elsevier, Amsterdam, 1997 Search PubMed.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- J. J. McKinnon, F. P. A. Fabbiani and M. A. Spackman, Cryst. Growth Des., 2007, 7, 755–769 CrossRef CAS.
- S. A. Moggach, S. Parsons and P. A. Wood, Crystallogr. Rev., 2008, 14, 143–184 CrossRef CAS.
- A. Parkin, G. Barr, W. Dong, C. J. Gilmore, D. Jayatilaka, J. J. McKinnon, M. A. Spackman and C. C. Wilson, CrystEngComm, 2007, 9, 648–652 RSC.
- G. Barr, W. Dong, C. J. Gilmore, A. Parkin and C. C. Wilson, J. Appl. Crystallogr., 2005, 38, 833–841 CrossRef CAS.
- T. E. Clark, M. Makha, A. N. Sobolev and C. L. Raston, Cryst. Growth Des., 2008, 8, 890–896 CrossRef CAS.
- K. Aburaya, K. Nakano, K. Sada, N. Yoswathananont, M. Shigesato, I. Hisaki, N. Tohnai and M. Miyata, Cryst. Growth Des., 2008, 8, 1013–1022 CrossRef CAS.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC.
- P. Munshi, B. W. Skelton, J. J. McKinnon and M. A. Spackman, CrystEngComm, 2008, 10, 197–206 RSC.
- M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2008, 10, 377–388 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, ( 2004) Gaussian, Inc., Wallingford CT Search PubMed.
- J. Gruber, A. Zawaira, R. Saunders, C. P. Barrett and M. E. M. Noble, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2007, 63, 50–57; A. J. McCoy, V. C. Epa and P. M. Colman, J. Mol. Biol., 1997, 268, 570–584 CrossRef CAS; N. Muzet, B. Guillot, C. Jelsch, E. Howard and C. Lecomte, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8742–8747 CrossRef CAS.
- M. Makha, J. J. McKinnon, A. N. Sobolev, M. A. Spackman and C. L. Raston, Chem.–Eur. J., 2007, 13, 3907–3912 CrossRef CAS.
- M. Norret, M. Makha, A. N. Sobolev and C. L. Raston, New J. Chem., 2008, 32, 808–812 RSC.
- X. X. Meng, PhD Thesis, University of New England, 2004.
- A. M. Pendas, V. Luana, L. Pueyo, E. Francisco and P. Mori-Sanchez, J. Chem. Phys., 2002, 117, 1017–1023 CrossRef CAS.
- G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356 CrossRef CAS.
- G. M. J. Schmidt, Pure Appl. Chem., 1971, 27, 647–678 CAS.
- F. H. Herbstein, J. Appl. Crystallogr., 1991, 24, 1080–1081 CrossRef.
- F. L. Hirshfeld and K. Mirsky, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1979, 35, 366–370 CrossRef.
- K. Mirsky, Acta Chim. Hung., 1993, 130, 197–204 CAS.
- A. I. Kitaigorodsky, Organic Chemical Crystallography, Consultants Bureau, New York, 1961 Search PubMed.
- A. I. Kitaigorodsky, Molecular crystals and molecules, Academic Press, New York, 1973 Search PubMed.
- B. K. Vainshtein, V. M. Fridkin and V. L. Indenbom, Modern Crystallography II, Springer-Verlag, Berlin, 1982 Search PubMed.
- D. Jayatilaka, D. J. Grimwood, A. Lee, A. Lemay, A. J. Russell, C. Taylor, S. K. Wolff, P. Cassam-Chenai and A. Whitton, TONTO—A system for computational chemistry, 2006 Search PubMed.
- R. E. Easton, D. J. Giesen, A. Welch, C. J. Cramer and D. G. Truhlar, Theor. Chim. Acta, 1996, 93, 281–301 CrossRef CAS; J. Li, C. J. Cramer and D. G. Truhlar, Theor. Chem. Acc., 1998, 99, 192–196 CrossRef CAS.
- C. C. Wilson, Crystallogr. Rev., 2007, 13, 143–198 CrossRef CAS.
- D. S. Middlemiss, M. Facchini, C. A. Morrison and C. C. Wilson, CrystEngComm, 2007, 9, 777–785 RSC.
Footnotes |
| † Although the interface with Gaussian is new, ab initio calculations have been previously available in CrystalExplorer using Tonto,47 which is distributed with CrystalExplorer. The advantage of using Gaussian—or other codes in the future—is the speed of computation and the access to a wider range of basis sets and computational methods. |
| ‡ Ab initio wavefunctions were obtained with Gaussian0333 and employed the Midi! basis set48 at the Hartree–Fock level and crystal molecular geometries with standardized bond lengths to hydrogen atoms. This analysis assumes that the carboxyl hydrogen atoms have been located accurately, and there is no disorder. Although this may be unlikely, as proton disorder in benzoic acid dimers is well known and increasingly well-studied by neutron diffraction49 and theory,50 for illustrative purposes we use the ordered structures reported in ref. 8. |
| § This trend in torsion angles is not obvious from Table 3 of ref. 8 but it emerges after recognizing that there are two molecules of each type, related by an improper rotation, and for which torsion angles differ by a change of sign. For comparison, there is only a small number of structures in the CSD which include 2-chlorobenzoic acids, and the relevant torsion angles in those structures span a similar range: 14° (CLBZAC and MAHWOI), 23° (HUHRAD), 33° (OCAYUM), 97° (UHAPUO) and 128° (MAHWUO). We also note that the subtleties of this conformational change cannot be taken into account in a graph set analysis of the hydrogen bonding patterns in these structures. |
| This journal is © The Royal Society of Chemistry 2009 |
