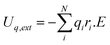Electric field tuning of oxygen stoichiometry at oxide surfaces: molecular dynamics simulations studies of zirconia
Subramanian K. R. S.
Sankaranarayanan
,
Efthimios
Kaxiras
and
Shriram
Ramanathan
*
Harvard School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138. E-mail: shriram@deas.harvard.edu
First published on 21st August 2009
Abstract
Ultra-thin metal-oxides such as zirconia have tremendous technological applications such as electrolyte membranes for advanced solid oxide fuel cells, fuel cladding material for light water nuclear reactors, pressure tube materials for heavy water nuclear reactors and corrosion resistant coatings. Oxide non-stoichiometry is an important factor which significantly affects their functional properties and applicability. Here, we report on the ability to athermally control oxygen non-stoichiometry in ultra-thin zirconia films through local electric field perturbations from simulations. Variable charge molecular dynamics simulations indicate significantly enhanced oxidation kinetics on Zr (0001) substrate in the presence of an electric field. Natural oxidation with no field resulted in an amorphous oxide scale with a self limiting thickness of ∼10 Å which increased to ∼17–26 Å for applied electric fields of 1–10 MV/cm. Electric field (∼107 V/cm) lowers the activation energy barrier for ionic migration through the oxide film and leads to significantly increased oxygen incorporation into the oxide film. Activation energy barrier for oxidation decreased from 1.13 eV with no field to 0.08 eV for an applied field of 10 MV/cm. This manifests itself in the form of dramatic density and stoichiometry improvements of the grown ultra-thin oxide film, as indicated by the calculated structural and dynamical correlation functions. Oxide stoichiometry (O/Zr ratio) for natural oxidation was 1.42 indicative of a sub-stoichiometric and oxygen deficient oxide which increased to near stoichiometric value of 1.86 for 10 MV/cm field assisted oxidation. The simulation findings agree well with previously reported experimental observations. Our results demonstrate a pathway to athermally control oxygen concentration in near-surface regions that is of great importance to technologies utilizing ultra-thin oxides ranging from catalysis, energy and electronic device technologies.
Broader impactHigh quality ultra-thin oxide films such as zirconia are of tremendous importance in energy sciences and technologies. Controlling oxide stoichiometry and oxygen concentration in the near surface regions of ultra-thin oxide films has a significant bearing on the functional properties of the synthesized oxide film and is of great significance. In this work, we show that atomic scale control of oxygen concentration in the near surface region of complex ultra-thin oxide films is possible via externally applied electric fields (∼107 V/cm). Zirconia ultra-thin films grown in the presence of electric field (∼107 V/cm) are shown to have significantly improved rates of oxygen incorporation compared to native oxide. Precise understanding of the microscopic processes involved in electric field assisted oxidation is provided by the atomistic models employing dynamic charge transfer between atoms. We find that lowering of activation energy barriers in the presence of electric fields is responsible for the dramatic density and stoichiometry improvements in ultra-thin oxide films. Our atomistic simulations demonstrate a pathway to athermally tune oxygen concentration in the near surface regions of complex oxides that is of great importance to contemporary problems ranging from catalysis to energy and electronic device technologies. |
I. Introduction
Metal oxide thin films are of great interest from various scientific and technological aspects. Ultra-thin oxide films find applications in several different areas including heterogeneous catalysis, microelectronics, chemical sensing, and passivation films for corrosion inhibition.1 One such technologically important oxide is zirconia which is used in the nuclear industry as a structural material for nuclear power reactors and in the chemical industry for corrosion protection.2,3 Other applications include alternate gate dielectrics in advanced transistors,4 electrolyte membrane for advanced solid oxide fuel cells,5 and also as fuel cladding material for light-water nuclear reactors and pressure tube materials for heavy-water nuclear reactors.3 Additionally, zirconium oxide is used for its high-temperature resistance in glass, ceramic, and coating technologies.6The method of oxide synthesis can have a significant bearing on their functional properties.7 The initial stage of metal oxidation and oxide growth can involve a number of different physical and chemical processes.8 These include physical and chemisorption of oxygen, nucleation and growth of oxide islands and/or a three dimensional oxide film covering the metal surface. The oxide-film growth is usually governed by the coupled currents of cations and/or anions, as well as electrons diffusing through the developing oxide film.9 The oxidation process for metals such as zirconium is further complicated by the possibility of formation of various intermediate non-stoichiometric oxides. The kinetics of oxide growth and the microstructure of the developing oxide film i.e. structure, morphology and chemical composition are strongly correlated to their chemical and physical properties. Examples include electric conductivity, corrosion resistance, and thermal, chemical and mechanical stability. In particular, oxide non-stoichiometry and density have been found to have an important role in determining their properties and applicability.10,11
Oxygen defects play a fundamental role in determining the physical and chemical properties of oxide materials.12 This is especially true for surface oxides where several kinds of point defects can exist making them exhibit a rich and complex chemistry. One such important defect in oxides is the oxygen vacancy which can be formed by the following reduction reaction:
The formation of such point defects depends both on thermodynamics as well as kinetics (particularly in non-equilibrium processing). While oxide non-stoichiometry can be advantageous in some cases, it is undesirable in others.13,14 Non-stoichiometric oxide due to oxygen defects can alter the electrical conduction phenomena in titania and thereby affect the performance of solar cell devices utilizing such oxides.13 For example, the conduction electrons created during the vacancy formation reaction shown above may improve electrical conductivity in oxides such as titania. Similarly, in heterogeneous catalysis, these defects can act as active sites and promote catalytic activities. On the other hand, non-stoichiometric surface oxides utilized as passivation layers have been found to exhibit poor corrosion resistance. Zimina et al. studied the influence of surface oxides of variable composition and non-stoichiometry on the general corrosion resistance of ferritic chromium steel type 08H17T.14 Surface oxide of nearly stoichiometric composition provided better passivation of steel in sulfuric acid when compared with that for non-stoichiometric oxide.14 In another investigation, zirconia thin film dielectrics prepared by natural oxidation were found to be non-stoichiometric due to oxygen deficiency and exhibited poor electrical characteristics.15 Optical properties of ferrous oxides were similarly found to be strongly correlated to the oxygen stoichiometry.16 Other examples include nickel oxide, where non-stoichiometry is found to result in higher activation energy of electrical conductivity.17 The properties of oxide materials are thus very sensitive to oxygen stoichiometry, which depends critically on the processing and synthesis conditions. In general, the presence of oxygen defects in complex oxides has a significant influence on a number of technologically important areas ranging from catalysis to corrosion.
Zirconium oxides represent one of the most technologically important materials whose properties are strongly influenced by the oxide stoichiometry. Stoichiometric zirconium oxide catalysts exhibited increased activity and selectivity towards industrially relevant oxidation reactions such as the strongly exothermic oxidation of carbon monoxide to carbon dioxide, ethylene to acetaldehyde, and acetylene to ethenone.18 Sub-stoichiometric oxygen deficient oxide films are known to have poor electrical conductivity, reduced corrosion resistance, as well as very poor thermal, chemical and mechanical stability.19 When oxide scales of high-k materials such as ZrO2 are oxygen deficient and sub-stoichiometric, leakage currents increase drastically which leads to unwieldy power consumption and reduced device reliability.19 Similarly, sub-stoichiometric ZrO2 also have increased O2− vacancy concentration in the oxide lattice, which drastically reduces their corrosion resistance.
One of the methods to minimize oxide non-stoichiometry involves the use of electrical field to stimulate oxide growth beyond that possible through thermal diffusion.20,21 Recent experimental studies have shown that oxide films that are grown under the influence of electric field as well as under photon exposure have dramatically different oxide microstructure compared to those synthesized naturally.10,21,22 UV photon interaction with molecular oxygen leads to the creation of activated atomic oxygen which can help overcome the activation barrier for chemisorption, leading to significantly increased rates of oxygen incorporation.23 Additionally, UV-light induced high-field migration also enhances the ionic currents within the growing oxide film which comprises the electric field effect.24 Several theories of metal oxidation suggest that the presence of a large uniform electric field (E0 = −VM/L) both in the oxide and at the metal-oxide interface due to contact potential (VM) can lower the activation energy barrier for ionic motion, even at temperatures that are otherwise low for appreciable thermal diffusion. The electric contact potential is termed the Mott Potential (VM) and represents the initial difference between the metal Fermi level and the oxygen O-level. Increasing the electrostatic potential through externally applied electric field leads to athermal stimulation of the ion diffusion, allowing for higher film growth than the saturation limit obtained using natural oxidation.21,22 These electron enhanced oxidation phenomena have been explained on the basis of the continuum models, such as that those formulated by Cabrera–Mott9 and Fromhold.25 Although considerable efforts have been directed to the study of these metal oxide surfaces, much remains to be understood regarding the origin of their properties at the atomic level.
In this work, mechanistic details of the electric field assisted oxidation kinetics and oxide growth at atomistic scale is elucidated using oxidation of Zr (0001) substrate as a model system. Variable charge molecular dynamics simulation is used to investigate the initial oxidation kinetics and ultra-thin oxide growth on the surface of Zr under the influence of electric fields. We evaluate the structural and morphological differences in the growing oxide film using dynamical correlation functions. The evolution of charges, self-limiting oxide thicknesses and atomic diffusivities under the varying electric fields are used to clearly explain the experimentally observed enhancement in the oxidation kinetics and subsequent improvement in the quality (density and stoichiometry) of the grown oxide film.
II. Computational details
The MD simulations employ a potential model that allows for variable and dynamic charge transfer between atoms and is capable of treating both metallic and ceramic systems as well as bond formation and bond breakage involved in oxidation processes on metal surfaces.26 Details of the potential model employed in this work can be found in ref. 27. The CTIP potential model comprises of non-electrostatic EAM potential model for the metallic region and electrostatic model for the ionic region. The EAM potentials for Zr metal have been well fitted to the lattice constant, cohesive energy, bulk modulus, shear modulus, anisotropic ratio, and the pressure derivative of the bulk modulus and show good agreement with available experimental and ab-initio simulation results. Details of these can be found in ref. 28. Similarly, the input properties of the oxide are the charge in the equilibrium bulk crystal, the electrostatic energy, the cohesive energy, the lattice constant, and the single-crystal elastic constants and parameterization of the CTIP potential model was carried out to closely fit and reproduce these properties. Additionally, the charge distribution as well as the magnitude of the charges in metal-oxide hetero-structures was accurately captured by the CTIP model. Zhou et al. have successfully used the CTIP potential model to predict surface relaxation and charge variations in various regions of a multilayer system including at free metal oxide surfaces, inside metal alloy bulk, inside metal oxide bulk, and at metal/metal oxide interfaces. Details of this potential model have been described in ref. 28 by Zhou et al. as well as our previous investigation.29 In this work, we consider the additional effect of electric field E (V/m) in these simulations. The electric field contributes an additional energy arising from the charges on the ions:The charges on the atoms are obtained dynamically using the charge relaxation procedure which minimizes the electrostatic energy subject to the electro-neutrality principle. The applied electric field was varied from 1 to 10 MV/cm to study the kinetics of field induced oxidation.
The set-up of the oxidation simulations is as follows: A slab of hcp Zr with dimensions (32 × 16 × 26 Å) was formed from an hcp unit cell. The surfaces were generated by artificially increasing the x-direction and introducing two vacuum slabs on each side of the metal substrate (Fig. 1). This unit cell was repeated infinitely though 3-D space by applying periodic boundary conditions. This configuration allowed for accurate computation of the Coulomb interaction by the Ewald summation technique.30 The substrates are then subjected to an equilibration procedure, which starts by annealing in the temperature range 0 K to 300 K in steps of 20K. For each temperature a run of 10000 MD steps using isokinetic MD was performed. These first equilibration runs are performed by ignoring the dynamic charge transfer between zirconium atoms since the charges are assumed to be zero for a pure metallic system. We performed an additional equilibration run of 10000 steps at 300 K by including the charge dynamics. As expected, we find that the atomic charges fluctuate around a zero value in the pure metal with a magnitude of ±0.08e (where e = 1.6 × 10−19 C) at the two outer layers and of ±0.02e in the bulk.
 | ||
| Fig. 1 Schematic showing the simulation set-up: unit cell of substrate and the vacuum slabs surrounding it. | ||
After these equilibration runs, we start to oxidize the metal substrate which marks the beginning of the production period. The oxidation of the Zr metal substrates is initiated by introducing O2 molecules in the vacuum slab with their x, y and z positions chosen randomly. The oxygen number density is maintained constant at approximately 0.004/Å3 in all the cases. The velocities of O2 molecules are chosen from a Maxwell–Boltzmann distribution corresponding to the required temperature. To ensure that the oxidation of the metal substrate proceeds along one direction, reflecting boundary conditions are imposed on the atoms and molecules that might reach the simulation box limit located at +3Lx/2. This methodology has been adopted in the oxidation simulations of Al by Hasnaoui et al.32 and Campbell et al.31 The equations of motion are integrated with time steps Δt = 1 fs for both short range and long range forces. The atomic charges were updated every 100 time steps such that the electrostatic energy is minimized subject to the constraint of electro-neutrality. Canonical MD simulations employing the Nose–Hoover thermostat is utilized to study low temperature metal oxidation in the presence and absence of electric field at various temperatures. The MD simulations were stopped when fragments of oxide species are ejected into the gas phase owing to localized melting of the surfaces, which occurs when the limiting thickness of the growing oxide film is reached.32,33 This is attributed to the accumulation of dissociated oxygen at the metal surface upon reaching the slow growth rate or the limiting regime, when their further intake into the metal substrate is impeded. This leads to heating up of this interface which is difficult to dissipate. Such localized melting upon reaching the saturation thickness has also been observed in previously reported MD simulations of oxidation of Al and Al–Ni surfaces.32,34
III. Results and discussion
We compare the oxidation kinetics and oxide growth on Zr surfaces in the presence of varying externally applied electric fields. Structure and dynamical correlations in the metal/oxide/gas environments are used to gain insights into the evolution and morphology of the growing oxide film. The effects of temperature on the oxidation kinetics are also discussed. The activation energy barriers for oxidation of metal surfaces under the influence of electric fields are derived from the simulated oxidation kinetic curves at various temperatures. The atomic trajectories generated using MD simulations are also used to identify the diffusion mechanisms associated with the oxide growth and explain the experimentally observed improvements in oxide quality.A. Enhanced oxygen incorporation kinetics in the presence of electric field
The influence of the electric field on the evolution of the simulated oxide-film thickness for Zr (0001) oxidation up to its limiting thickness for natural oxidation is shown in Fig. 2. Our simulations indicate that the oxide film growth shows an initial rapid increase followed by a slower growth phase beyond 50 ps of simulation time. We observe that the room temperature oxidation kinetics and oxide growth are considerably enhanced in the presence of externally applied electric fields in the 1–10 MV/cm range. Increasing the electric field from 1 to 10 MV/cm resulted in faster kinetics and an earlier onset of the slower growth phase. The self-limiting thickness of oxide film in the case of natural oxidation corresponds to approximately 1.0 nm. The simulated self limiting thickness of ∼1 nm in the case of natural oxidation (with no field) agrees well with the 1.2 nm thickness obtained experimentally for O2oxidation at 373 K by Jeurgens et al.35,36 Experimental studies by Lyapin et al. also report zirconium oxide thicknesses to vary from 1–2 nm in the 373–573 nm range.37 We find that the growth of the oxide scale on Zr surface is primarily inwards and is primarily attributed to the movement of anions towards the interior of the metal substrate. Upon increasing the electric field from 1 to 10 MV/cm, we find that the self-limiting thickness of the oxide film formed varies from approximately 1.7 to 2.6 nm at 300 K. This can be seen in the snapshots shown in Fig. 3. To the best of our knowledge, there are no available experimental studies on the electric-field assisted oxidation of Zr (0001) surface. However, such an enhancement in the oxidation kinetics in the presence of electric field has been observed by Popova et al.20,21 and Zhukov et al.38 in their experimental studies on electron-stimulated aluminum oxidation. In this work, we have maintained a constant O2 pressure. The effects of changing O2 pressure on the oxidation kinetics has been performed in a separate investigation on Al substrates. The oxidation kinetics increases with gas pressure and we expect similar behavior for the oxidation of Zr substrates. | ||
| Fig. 2 Variation of simulated oxide film thickness with the exposure time for oxidation in O2 environment at various applied electric field and room temperature. | ||
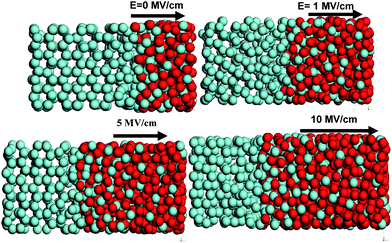 | ||
| Fig. 3 Snapshots showing enhanced oxidation of Zr (0001) under the effect of the electric field. Oxygen atoms are shown in dark color. | ||
B. Oxide scale analysis (natural vs. field assisted growth)
To perform the oxide scale analysis (Fig. 4 and 5), the distribution functions were computed over a 5 ps time interval with simulation trajectories collected at every step i.e. 1 fs. Thus, the averaging was carried over 5000 different configurations which are sufficiently large to ensure that the distribution functions obtained are not influenced by statistics. Identical analysis procedure was carried out for the various cases i.e.oxidation with no field and applied electric field of 1, 5 and 10 MV/cm to facilitate comparisons between the various simulated cases.
 | ||
| Fig. 4 Pair distribution function Zr–O in Zr/O system taken at 150 ps of exposure time for the case of natural oxidation with (a) no field and an applied electric field of 1–10 MV/cm. Inset shows that the distribution becomes more uniform with increasing electric field. | ||
 | ||
| Fig. 5 O–Zr–O bond angles in the grown oxide film for natural oxidation with (a) no field (b) varying values of applied electric field. | ||
i. Pair distribution function. The pair distribution function (PDF) of the atoms in the oxide film as well as partial PDF for each type of atoms Zr–O PDF is shown in Fig. 4(a) and (b) for oxidation with molecular oxygen in the absence and presence of external electric fields, respectively. The position of the peaks in gZrO(r) typically gives estimate of the nearest neighbor distances and therefore the Zr–O bond length. We observe that the Zr–O PDF in the case of O2oxidation with no field shows a distribution of bond lengths from 2.16 to 2.4 Å in the oxide scales. The oxide scales formed in all the cases are amorphous in nature. Experimental studies by Jeurgens et al. on natural oxidation of Zr substrates indicate the formation of a non-stoichiometric oxide film.35,36 For such non-stoichiometric oxides, the bond lengths show a distribution reflecting the existence of multiple non-stoichiometric species. The simulated bond-lengths shown in Fig. 4(a) for natural oxidation agree well with the experimentally reported bond length distribution with an average of 2.28 Å for oxide scale formed on Zr (0001) substrate.39 On the application of external field, the oxygen incorporation into the growing oxide film is increased and it results in the formation of a more uniform, thicker and stoichiometric film. These details are discussed in the subsequent sections in the manuscript. The fusion of the peak and shoulder at higher applied electric field can be attributed to the significant improvement in oxide stoichiometry and density which results in a more uniform distribution of bond-length, hence the presence of a single peak at an applied electric field of 10 MV/cm.
As seen in Fig. 4(b), the Zr–O peak shifted from 2.45 Å in the case of natural oxidation with 1 MV/cm to 2.3 Å for the 10 MV/cm applied electric field. Increasing the electric field from 1 to 10 MV/cm thus results in shortening of bond-length. This bond-length shortening is a result of increased oxide density due to increased rate of oxygen incorporation in the presence of externally applied electric field. The coordination numbers for Zr, obtained by integrating gZrO(r) up to 3.2 Å, are 3.1 and 3.4 for O2oxidation with no field and 10 MV/cm, respectively. The PDF for O–O also showed similar shifts in the peak positions related to the change in the relative Zr and O densities upon applying the electric field. It should be noted that the improvements in oxide stoichiometry and density upon application of external electric field has been observed in experimental studies of electric-field assisted oxide growth on Al substrates.20,21 Also, photon-assisted oxide synthesis, which involves the electric field effect, has been shown to result in growth of Zr oxide films which are more stoichiometric and oxygen enriched compared to native oxide film.10,40
ii. Bond angle distribution. Fig. 5(a) and (b) show O–Zr–O bond-angle distribution in the interior of the oxide scales for Zr oxidation using molecular oxygen with and without externally applied electric field, respectively. For an amorphous and non-stoichiometric oxide scale, the bond angle distribution is broad and has multiple peaks and hence it is difficult to establish the exact nature of coordination. For the case of lower applied field (1 and 5 MV/cm), the amorphous oxide scale has a non-stoichiometric value of 1.57 and 1.73, respectively and have more than one peak located at ∼115° and 113°. For the case of oxidation with applied electric field of 10 MV/cm, we find that the angle is ∼112°, which is close to a tetrahedral coordination. It should be noted that the amorphous oxide scale formed for this field is more uniform and nearly stoichiometric (O/Zr = 1.86). This level of distortion in the bond angles (112–115°) has been observed in case of several other amorphous systems, which typically exhibit tetrahedral coordination.41 Therefore, it appears that as the electric field is increased, the oxide film formed becomes more stoichiometric and the distribution is more uniform with the bond angles approaching values closer to 109° which corresponds to an ideal tetrahedral coordination.
A slight shift in the peaks to smaller angles was observed upon increasing the electric field from 1 to 10 MV/cm. This is reflective of a decrease in the zirconium density. On the other hand, the O–Zr–O bond-angle distribution in the O2 oxide scale shown in Fig. 5(a) is very different from Fig 5(b). The calculated O–Zr–O bond angle distribution in the native oxide scale shows the presence of multiple peaks, reflecting the possibility of the existence of multiple non-stoichiometric oxide species. The sub-stoichiometric oxide formation observed across the oxide scale in the case of natural oxidation might be the result of oxygen deficient environment attributed to reduced oxidation kinetics.
| Field | O/Zr |
|---|---|
| Natural | 1.42 |
| 1 MV/cm | 1.57 |
| 5 MV/cm | 1.73 |
| 10 MV/cm | 1.86 |
 | ||
| Fig. 6 Evolution of O/Zr stoichiometry in the growing oxide film as a function of oxidation time for the oxidation of the bare Zr (0001) substrate at 300 K for varying values of applied electric field. | ||
We have further computed the variation in oxide stoichiometry across the thickness of the oxide films as shown in Fig. 7. In case of oxidation of Zr (0001) with no electric field, our simulation results indicate a gradation of oxygen stoichiometry across the oxide thickness such that the oxygen densities are lower at the metal-oxide interface and higher at the oxide-gas interface. This relative enrichment of the cations in regions close to the oxide-metal interface has also been observed in case of natural oxidation of Zr substrate by Jeurgens et al.35 When the electric field is increased from no field to 10 MV/cm, the O/Al ratios increase from 1.28 to 1.80, 1.44 to 1.86 and 1.52 to 1.92 at the oxide-metal, oxide-interior and oxide-gas interfaces, respectively (Table 2).
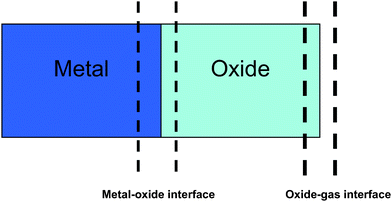 | ||
| Fig. 7 Schematic showing the different interfaces across which the oxide stoichiometry has been computed. The calculated O/Zr ratios are summarized in Table 2. | ||
In a previous investigation on electric field assisted oxidation of Al, we had indicated that a possible mechanism for the observed increase in the oxidation kinetics and oxide film quality in the presence of the electric field involves the transformation of chemisorbed O species on the surface to the oxidic species. Increasing the electric field leads to a significant increase in the diffusivity of the oxygen atoms into the substrate. The high oxidation rates are induced by the presence of an electrostatic potential across the developing oxide film, which lowers the energy barriers for inward O anion migration from the oxide-gas interface into the oxide film as well as for outward migration of Zr cations from the parent metal substrate into and through the developing oxide film towards the reacting oxide/gas interface. The Mott potential VM is the result of the equilibrium set up between the electronic states at the Fermi level in the metal and the acceptor levels provided by oxygen atoms or ions chemisorbed onto the oxide surface.8 It should be noted that the electrostatic potential in the outer part of the oxide film in case of thermal oxidation decreases linearly with the oxide film thickness. Increasing the electrostatic potential through an externally applied electric field leads to artificial stimulation of the ion diffusion, allowing for higher film growth than the saturation limit obtained using thermal oxidation.21 This can explain the increase in oxidation kinetics and improvement in oxide stoichiometry (Table 1) in the presence of an external electric field.
C. Mechanism of electric field enhanced oxide growth
The activation energy barrier lowering due to the presence of electric field can be computed using the theory of oxidation kinetics in ultra-thin films in conjunction with the simulation data derived from the oxidation kinetic curves at various temperatures.19 The oxidation kinetic curves were obtained in the 300–600 K temperature range for natural oxidation of Zr (0001) in the presence and absence of electric field. They are depicted in Fig. 8(a) and (b) for electric fields of 1 and 5 MV/cm, respectively.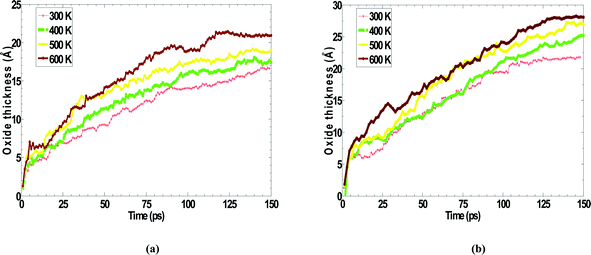 | ||
| Fig. 8 Variation of oxidation kinetics with temperature for an applied electric field of (a) 1 MV/cm (b) 5 MV/cm. | ||
The methodology adopted here for calculation of activation energy barrier was discussed in detail in our previous work and is briefly summarized here.33 In case of field assisted migration of an ion between two adjacent sites, the general expression for the potential (W) to be overcome is given as:19
 | (1) |
In Eqn (1), W0 represents the intrinsic barrier for ionic jumps between two positions in the oxide film, L is the oxide film thickness, and λ is a term which depends on the oxide structure, q represents the charge on the ion, and a represents the jump length. The second term on the R.H.S. represents the energy barrier lowering by an electric field E across the oxide film, and the structure term (λ) represents dependence of activation energy on the structural changes in the oxide film associated with the film growth. The oxidation kinetic curves such as those shown in Fig. 8 can be fitted to a logarithmic growth curve as shown below:19
 | (2) |
Here, the term µ(T) is a temperature dependent term and is defined by:
 | (3) |
Rearranging Eqn (2) allows us to write the following:
| L(t) = α ln(t) + β | (4) |
Parameters α and β are defined by  and
and  . After fitting the oxidation kinetic curves such as those in Fig. 8 to Eqn (4), it is possible to get the estimates of the two parameters α and β. Utilizing these two parameters, estimates of the structure term λ and µ (T) can be obtained. The term
. After fitting the oxidation kinetic curves such as those in Fig. 8 to Eqn (4), it is possible to get the estimates of the two parameters α and β. Utilizing these two parameters, estimates of the structure term λ and µ (T) can be obtained. The term  represents the Arrhenius dependence on the temperature as seen in Eqn (3). The fits of
represents the Arrhenius dependence on the temperature as seen in Eqn (3). The fits of  term to the inverse of temperature allow us to deduce the activation energy barrier for the various cases (molecular oxygen with no field, 1, 5 and 10 MV/cm, respectively).
term to the inverse of temperature allow us to deduce the activation energy barrier for the various cases (molecular oxygen with no field, 1, 5 and 10 MV/cm, respectively).
 | (5) |
 | (6) |
 | (7) |
 | (8) |
Using these Arrhenius fits shown in Eqn (5)–(8), it is possible to get an estimate of the term  . We find this to be 0.029 ± 0.01, 0.092 ± 0.01, 0.13 ± 0.01 and 0.20 ± 0.01 eV for natural oxidation with 0, 1, 5 and 10 MV/cm respectively. If the value of the electric field E is known, then it is possible to get the exact estimate of the energy barrier W0. The electric field produced across the oxide film lowers the energy barriers for the outward ‘hopping’ of cations into and through interstices of the oxygen ion arrangement of the developing oxide film and is given by E = Vk/L, where Vk represents the established potential and L represents the thickness of the oxide film.8 Based on the low temperature oxidation studies of zirconium by Jeurgens et al., it is possible to get an estimate of the established kinetic potential (Vk ∼ 2 V).35,36 In case of field assisted simulations, there is an additional lowering due to the externally applied electric field. In the present simulations, the self limiting oxide film thickness corresponding to field-assisted, atomic and natural oxidation at room temperature corresponds to approx. 1.7, 2.2 and 2.6 nm, respectively. Additionally, the average charge q of the zirconium atoms in the oxide film interior was found to be approximately 3.4e for natural oxidation with no field and ∼3.5e for electric field assisted oxidation. The jump distance was approximated from the first peak distance in the pair distribution function for Zr–Zr (∼3.4 Å for natural oxidation with no field and 3.3, 3.2 and 3.2 Å with 1, 5 and 10 MV/cm, respectively). The computed activation energy barriers are summarized in Table 3.
. We find this to be 0.029 ± 0.01, 0.092 ± 0.01, 0.13 ± 0.01 and 0.20 ± 0.01 eV for natural oxidation with 0, 1, 5 and 10 MV/cm respectively. If the value of the electric field E is known, then it is possible to get the exact estimate of the energy barrier W0. The electric field produced across the oxide film lowers the energy barriers for the outward ‘hopping’ of cations into and through interstices of the oxygen ion arrangement of the developing oxide film and is given by E = Vk/L, where Vk represents the established potential and L represents the thickness of the oxide film.8 Based on the low temperature oxidation studies of zirconium by Jeurgens et al., it is possible to get an estimate of the established kinetic potential (Vk ∼ 2 V).35,36 In case of field assisted simulations, there is an additional lowering due to the externally applied electric field. In the present simulations, the self limiting oxide film thickness corresponding to field-assisted, atomic and natural oxidation at room temperature corresponds to approx. 1.7, 2.2 and 2.6 nm, respectively. Additionally, the average charge q of the zirconium atoms in the oxide film interior was found to be approximately 3.4e for natural oxidation with no field and ∼3.5e for electric field assisted oxidation. The jump distance was approximated from the first peak distance in the pair distribution function for Zr–Zr (∼3.4 Å for natural oxidation with no field and 3.3, 3.2 and 3.2 Å with 1, 5 and 10 MV/cm, respectively). The computed activation energy barriers are summarized in Table 3.
| Oxidation | Activation energy (eV) |
|---|---|
| No field | 1.13 |
| 1 MV/cm | 0.71 |
| 5 MV/cm | 0.36 |
| 10 MV/cm | 0.08 |
The decrease in the activation energy barrier for ionic migration is responsible for the increased oxidation kinetics observed in Fig. 2 and enhanced self-limiting thickness shown in Fig. 3. Thus, increasing the electrostatic potential through the externally applied electric field leads to artificial stimulation of the ion diffusion and allows for higher film growth than the saturation limit obtained using thermal oxidation. This results in the formation of a uniform and thicker oxide film with improved oxide stoichiometry and density. The observed differences in the oxygen distribution can also be evaluated using the calculated in-plane and out-of-plane oxygen diffusivities across the developing oxide film. We calculated the atomic diffusivities based on the mean square displacements computed over 1 ps interval for oxidation at 300 K. The in-plane diffusion coefficients dictate the extent of uniformity across the developing oxide film, whereas the out-of-plane diffusion coefficients dictate the extent of oxide growth. Typical calculated in-plane atomic diffusivities in the oxide film are in the range of 7–9 × 10−6 cm2/s for natural oxidation in the oxide interior at 50 ps. We find that both the in-plane and out-of-plane diffusion coefficients are significantly higher in the presence of electric field. For example, the corresponding in-plane atomic diffusivities in case of natural oxidation with electric field of 10 MV/cm are in the range of 1–2 × 10−5 cm2/s. The higher in-plane diffusion ensures that the 2-D oxide growth in a particular atomic layer is completed before the growth front can proceed to the next atomic layer. This results in a more uniform distribution of oxygen atoms at the oxide interior in the presence of the electric field. These results are in good agreement with experimental room temperature oxidation of Zr.36,40
Similarly, the out-of-plane diffusivities of oxygen atoms at the metal-gas interface and zirconium atoms at the oxide-metal interface are higher for field-assisted oxidation than that observed for natural oxidation. Our analysis of Zr and O diffusivities in the shells located at the metal-oxide and oxide-gas interface for exposure time less than 100 ps indicates 80–90% higher diffusivities for molecular oxidation in the presence of electric field (10 MV/cm). For example, in case of natural oxidation, the O and Zr diffusivities at 50 ps were found to be 3.8 × 10−6 and 5.1 × 10−6 cm2/s, respectively. On the other hand, the O and Zr diffusivities at 50 ps for field-assisted oxidation (i.e. 10 MV/cm) were 6.9 × 10−6 and 9.7 × 10−6 cm2/s, respectively. The higher out-of-plane diffusivities in the presence of externally applied electric field result in the enhanced self limiting thicknesses observed in Fig. 2.
IV. Conclusions
In conclusion, we report a molecular dynamics simulation study of Zr oxidation using molecular (O2) oxygen with and without externally applied electric field. These simulations include dynamic charge transfer among atoms and are used to investigate the differences in oxidation kinetics, nanoscale zirconium oxide growth as well as the structure and morphology of the growing zirconium oxide films due to an electric field. The presence of the electric field (∼107 V/cm) is found to increase the oxidation kinetics. The self-limiting oxide film thickness increased from 1 nm for natural oxidation with no field to 2.6 nm for an applied field of 10 MV/cm. Structural analysis indicates enhanced self limiting thicknesses using externally applied electric fields in the 1–10 MV/cm for oxide films obtained after 150 ps of simulation time at 300 K. Ionic migration through the oxide film is increased due to lowering of the activation energy barrier via externally applied electric field and is consistent with the Cabrera–Mott theory of low temperature oxidation. Activation energy decreases from 1.13 eV for natural oxidation with no field to 0.08 eV for an applied electric field of 10 MV/cm. We find that the Zr and oxygen diffusivities in the oxide are about 80–90% higher for electric-field assisted oxidation (∼10 MV/cm). The higher atomic diffusivities result in a more uniform oxide thickness as well as increased oxygen stoichiometry across the oxide film for electric field assisted oxidation. Application of external electric field (∼10 MV/cm) drives the surface chemisorbed oxygen into the oxide interior leading to a dramatic improvement in the stoichiometry and density of the oxide film. The same is reflected in the calculated O/Zr composition ratio, bond lengths and bond angle distribution functions. Oxide stoichiometry (O/Zr) improved from 1.42 for natural oxidation to 1.86 for 10 MV/cm field assisted oxidation. The simulation results of this work are consistent with the experimental results on room temperature Zr oxidation.36,40 The results provide a pathway for athermally controlling oxygen concentration in near-surface regions and could be of significance for various technological applications utilizing complex oxide films.Acknowledgements
Financial support from the Office of Naval Research is gratefully acknowledged.References
- A. Stierle, F. Renner, R. Streitel and et al., Science, 2004, 303, 1652 CrossRef CAS.
- J. P. Holgado, M. Perez-Sanchez, E. Yubero and et al. , Surf. Coat. Technol., 2002, 151–152, 449 CrossRef CAS.
- B. Cox, J. Nucl. Mater., 2005, 336, 331 CrossRef CAS.
- H. Kim, K. C. Saraswat and P. C. McIntyre, J. Mater. Res., 2005, 20, 3125 CrossRef CAS.
- J. H. Shim, C. C. Chao, H. Huang and et al. , Chem. Mater., 2007, 19, 3850 CrossRef CAS.
- S. N. Karlsdottir and J. W. Halloran, J. Am. Ceram. Soc., 2007, 90(10), 3233 CrossRef CAS.
- M. Tsuchiya, S. K. R. S. Sankaranarayanan and S. Ramanathan, Prog. Mater. Sci., 2009, 54(7), 981 CrossRef CAS.
- A. Atkinson, Rev. Mod. Phys., 1985, 57, 437 CrossRef CAS.
- N. Cabrera and N. F. Mott, Rep. Prog. Phys., 1949, 12, 163 CrossRef CAS.
- C. L. Chang, M. H. Engelhard and S. Ramanathan, Appl. Phys. Lett., 2008, 92(26), 3.
- C. L. Chang, S. K. R. S. Sankaranarayanan, Mark Engelhard and et al. , J. Phys. Chem. C, 2009, 113(9), 3502 CrossRef CAS.
- C. T. Campbell and C. H. F. Peden, Science, 2005, 309(5735), 713 CrossRef CAS.
- T. Bak, J. Nowotny and M. K. Nowotny, J. Phys. Chem. B, 2006, 110(43), 21560 CrossRef CAS.
- T. Zimina, E. Oshe, V. Dubkov and et al., J. Electrochem. Soc., 1998, 145(7), 2236 CrossRef CAS.
- S. Ramanathan, D. Muller, G. D. Wilk and et al. , Appl. Phys. Lett., 2001, 79, 3311 CrossRef CAS.
- S. Mrowec and A. Podgórecka, J. Mater. Sci., 1987, 22(12), 4181 CrossRef CAS.
- Y. Iida, K. Shimada and S. Ozaki, Bull. Chem. Soc. Jpn., 1960, 33(10), 1372 CrossRef CAS.
- G. E. Johnson, R. Mitric, E. C. Tyo and et al., J. Am. Chem. Soc., 2008, 130(42), 13912 CrossRef CAS.
- K. R. Lawless, Rep. Prog. Phys., 1974, 37, 231 CrossRef CAS.
- I. Popova, V. Zhukov and J. T. Yates, Appl. Phys. Lett., 1999, 75(20), 3108 CrossRef CAS.
- I. Popova, V. Zhukov and J. T. Yates, Phys. Rev. Lett., 2002, 89(27), 276101 CrossRef CAS.
- S. K. R. S. Sankaranarayanan, E. Kaxiras and S. Ramanathan, Phys. Rev. Lett., 2009, 102, 095504 CrossRef.
- E. T. Byram, T. A. Chubb and H. Friedman, Phys. Rev., 1955, 98, 1594 CrossRef CAS.
- C. L. Chang and S. Ramanathan, J. Electrochem. Soc., 2007, 154, G160 CrossRef CAS.
- A. Fromhold, Theory of Metal Oxidation. (North-Holland, Amsterdam, 1976) Search PubMed.
- T. J. Campbell, G. Aral, S. Ogata and et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205413 CrossRef.
- X. W. Zhou, H. N. G. Wadley, J. S. Filhol and et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 035402 CrossRef; X. W. Zhou, H. N. G. Wadley, R. A. Johnson and et al. , Acta Mater., 2001, 49, 4005 CrossRef CAS.
- X. W. Zhou, H. N. G. Wadley, J.-S. Filhol and et al. , Phys. Rev. B, 2005, 68, 065402.
- S. K. R. S. Sankaranarayanan and S. Ramanathan, J. Phys. Chem. C, 2008, 112(46), 17877 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253 CrossRef.
- T. Campbell, R. K. Kalia, A. Nakano and et al. , Phys. Rev. Lett., 1999, 82, 4866 CrossRef CAS.
- A. Hasnaoui, O. Politano, J. M. Salazar and et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035427 CrossRef.
- S. K. R. S. Sankaranarayanan and Shriram Ramanathan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085420 CrossRef.
- A. Hasnaoui, O. Politano, J. M. Salazar and et al. , Surf. Sci., 2005, 579, 47 CrossRef CAS.
- L. Jeurgens, A. Lyapin and E. Mittemeijer, Acta Mater., 2005, 53, 4871 CrossRef CAS.
- L. Jeurgens, A. Lyapin and E. Mittemeijer, Surf. Interface Anal., 2006, 38, 727 CrossRef CAS.
- A. Lyapin, L. P. H. Jeurgens and E. J. Mittemeijer, Acta Mater., 2005, 53, 2925 CrossRef CAS.
- V. Zhukov, I. Popova and J. T. Yates, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(19), 195409 CrossRef.
- Y. M. Wang, Y. S. Li and K. A. R. Mitchell, Surf. Sci., 1995, 342, 272 CrossRef CAS.
- S. Ramanathan, D. Chi, P. C. McIntyre and et al., J. Electrochem. Soc., 2003, 150, F110 CrossRef CAS.
- J. Koga, F. Yonezawa, K. Nishio and et al. , J. Non-Cryst. Solids, 2004, 345–346, 742 CrossRef; Tetsuya Morishita, Phys. Rev. Lett., 2004, 93(5), 055503 CrossRef; G. Guitierrez, Revista mexicana de física, 2002, 48, 60 Search PubMed; S. P. Adiga, P. Zapol and L. A. Curtiss, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 064204 CrossRef.
- A. Lyapin, L. P. H. Jeurgens, P. C. J. Graat and et al. , J. Appl. Phys., 2004, 96, 7126 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2009 |