Interaction of internally mixed aerosols with light

Abstract

Atmospheric aerosols scatter and absorb solar radiation leading to variable effects on Earth’s radiative balance. Aerosols individually comprising mixtures of different components (“internally mixed”) interact differently with light than mixtures of aerosols, each comprising a different single component (“externally mixed”), even if the relative fractions of the different components are equal. In climate models, the optical properties of internally mixed aerosols are generally calculated by using electromagnetic “mixing rules”, which average the refractive indices of the individual components in different proportions, or by using coated-sphere Mie scattering codes, which solve the full light scattering problem assuming that the components are divided into two distinct layers. Because these calculation approaches are in common use, it is important to validate them experimentally. In this article, we present a broad perspective on the optical properties of internally mixed aerosols based on a series of laboratory experiments and theoretical calculations. The optical properties of homogenously mixed aerosols comprised of non-absorbing and weakly absorbing compounds, and of coated aerosols comprised of strongly absorbing, non-absorbing, and weakly absorbing compounds in different combinations are measured using pulsed and continuous wave cavity ring down aerosol spectrometry (CRD-AS). The success of electromagnetic mixing rules and Mie scattering codes in reproducing the measured aerosol extinction values is discussed.

---

Naama Lang-Yona

Naama Lang-Yona finished her MSc on optical properties of aerosols in the Weizmann Institute of Science. She did her BSc in Environmental Sciences at the Tel-Hai College. Naama has just started a PhD in atmospheric chemistry in the Weizmann Institute of Science and will work on correlating fungi in aerosols with allergies.

Ali Abo-Riziq

Ali Abo Riziq (PhD in Chemistry from University of Santa Barbara California, UCSB, 2005) is a Staff Scientist at the Weizmann Institute of Science. He joined Prof. Yinon Rudich’s group at 2005 for postdoctoral work on developing different cavity ring down aerosol spectrometers. His main research interests are the optical properties of aerosols.

Carynelisa Erlick

Carynelisa Erlick (PhD in Atmospheric Sciences, University of Chicago) is a senior lecturer at the Hebrew University of Jerusalem, Department of Atmospheric Sciences. Her main research interests are radiative transfer in the Earth's atmosphere and climate forcing. Her recent research involves accounting for the effect of mixed composition and nonsphericity of aerosol particles on their radiative properties.

Enrico Segre

Enrico Segre (PhD in Physics from the University of Turin, Italy, 1994), is currently a Staff Scientist at the Weizmann Institute of Science and was an assistant professor at the Polytechnic of Turin between 1995 and 2000. His main scientific interests are in non-linear aspects of fluid dynamics and in microfluidics.

Miri Trainic

Miri Trainic is a PhD student in atmospheric chemistry in the Weizmann Institute of Science. She did her BSc in Chemistry and Environmental Sciences in the Hebrew University of Jerusalem and her MSc in Environmental Diagnosis, at the Imperial College in London. Her current PhD work focuses on the optical properties of organic aerosols.

Yinon Rudich

Yinon Rudich received his BSc from Ben Gurion University (1987) and MSc and PhD degrees (honors) from the Weizmann Institute (1994). Following postdoctoral work at the National Oceanic and Atmospheric Administration in Boulder, he joined the Weizmann Institute of Science where he is currently a Professor in the Department of Environmental Sciences and Energy Research. His research interests include the chemistry and physics of organic aerosols and of mineral dust, optical properties of aerosols, aerosol–climate interactions and characterization of ambient atmospheric aerosols.

---

1. Introduction

Atmospheric aerosols, small solid or liquid particles suspended in the atmosphere, contain organic and inorganic compounds from anthropogenic as well as natural sources. Aerosols can be emitted directly into the atmosphere (primary aerosols) from various sources, such as fossil fuel combustion, biomass burning, soil and road dust, salt from sea spray, and biological materials (e.g., pollen, bacteria, etc.).^1,2 Secondary aerosols form in the atmosphere by condensation of gas phase compounds onto pre-existing particles, homogeneous nucleation of volatile or semi-volatile compounds to form nanometer-scale particles, or by heterogeneous and multi-phase reactions.^1,2 The latter two processes occur on aerosol surfaces, in the bulk of the aerosol, as well as within cloud drops.^1,3–6 The rate of secondary aerosol formation is controlled by temperature, relative humidity (RH), and the concentration of the nucleating and condensing compounds.⁷

In the visible range, aerosols affect atmospheric radiation balance, and hence climate, through three main processes: (1) direct scattering and absorption of incoming solar radiation (the direct effect), (2) by acting as cloud condensation nuclei (CCN), which control cloud reflectivity, extent, and lifetime (the indirect effect), and (3) by heating the atmosphere through absorption of incoming solar radiation (the semi-direct effect).^8–20 While the direct and indirect effects generally lead to a negative radiative forcing of climate or cooling by reducing the amount of solar radiation reaching the Earth’s surface, the semi-direct effect can lead to either cooling or warming, depending on whether the atmospheric absorption dominates (cooling the surface) or whether the corresponding reduction in low cloud cover and liquid water path dominates (warming the surface).²¹

Atmospheric aerosols contain a mixture of organic and inorganic components.²² The chemical constituents that make up atmospheric aerosols dictate their chemical and physical properties (chemical reactivity, interaction with radiation, hygroscopicity, optical properties, etc.). Aerosols that consist mostly of inorganic matter (such as sea salt, sulfate, nitrate)^23,24 and non-absorbing organic compounds (OC)^25–27 tend to be scattering, affecting climate through the direct effect. Aerosols that consist of elemental carbon (EC; soot),^10,28–31 mineral dust,^32,33 and certain moderately absorbing organics (“brown carbon”)^27,34–37 tend to be absorbing, affecting climate through the direct and semi-direct effects.¹⁸

The scattering and absorbing properties of aerosol constituents are characterized by various physical parameters, the most fundamental of which is the complex refractive index (RI = n + ik), where the real part (n) describes the ability of the constituent to reflect or scatter radiation, and the imaginary part (k) describes the ability of the constituent to absorb radiation. Both the real and the imaginary parts of the complex RI are functions of wavelength (λ).³⁸ Knowing the RI of aerosols enables the calculation of other radiative parameters relevant to the climate and is therefore extremely valuable for climate change modeling.^13,39–43 These radiative parameters include the scattering, absorption, and extinction (attenuation) coefficients (describing the e-folding of radiative intensity with distance: α_sca, α_abs, and α_ext = α_sca + α_abs, respectively). Other optical parameters include the optical depth (the extinction coefficient multiplied by the radiation propagation distance; τ_ext), the phase function (describing the angular pattern of scattered intensity for a single aerosol scattering event; P(θ_sca), where θ_sca is the scattering angle), the asymmetry parameter (the extent of forward scattering relative to backward scattering; g), and the single scattering albedo (describing the amount of scattering relative to total extinction; ϖ = α_sca/(α_sca + α_abs)).⁴⁴

Related to α_ext, the extinction efficiency (Q_ext) is defined as σ_ext/πr², where σ_ext is the aerosol extinction cross section (integrating the extinction cross section over the aerosol size distribution gives α_ext).^45,46 One way to obtain the complex RI of an aerosol constituent is by measuring Q_ext as a function of particle size for a homogeneous (spherical) aerosol comprised of the same constituent. The complex RI can then be obtained by fitting the measured Q_ext values to a Mie scattering curve, computed with readily available numerical subroutines that give the scattering solution to Maxwell’s equations as a function of particle size and wavelength, following Gustav Mie’s original derivation (see section 2).^45,47

In addition to the RI values of the chemical constituents that make up atmospheric aerosols, aerosol radiative parameter values are strongly influenced by the physical configuration of these constituents within the aerosol, i.e., by the aerosol microstructure.^45,48 As shown in Fig. 1, aerosols can appear as externally mixed (particles 1 and 2), heterogeneously internally mixed (i.e., coated particles; particles 3, 4, and 5), or homogeneously internally mixed (particles 6 and 7).^49–61

Fig. 1 Complex atmospheric aerosols (the combination of 1 and 2 in the same environment represents externally mixed aerosols, 3–5 represent different types of coated particles, and 6 and 7 represent different types of homogeneously mixed aerosols).

Homogeneous internally mixed aerosols form by processes such as evaporation of droplets containing several species with similar solubility and by simultaneous condensation of semi-volatile species. They can be found in a variety of combinations, including: (1) internal mixtures of several non-absorbing components (e.g., sodium chloride (NaCl) mixed with non-absorbing organics); (2) internal mixtures of non-absorbing components (e.g., ammonium sulfate (AS)) mixed with weakly absorbing components (e.g., humic-like substances (HULIS)); and (3) internal mixtures of non-absorbing components mixed with strongly absorbing components, such as mineral elements, metals, or brown carbon.^3,62–64

Coated particles can form by processes such as condensation of semi-volatile species on pre-existing particles, evaporation of droplets containing both soluble and insoluble components, dehydration of droplets containing two species with substantially different solubilities, and heterogeneous chemical reactions (e.g., oxidation, radical reactions, photochemistry, etc.) on aerosol surfaces, creating a shell with a different character. Like homogeneously internally mixed aerosols, coated particles can be found in a variety of combinations, including: (1) a non-absorbing core (e.g., NaCl) coated with another non-absorbing species (e.g., non-absorbing organics); (2) a non-absorbing core coated with a weakly absorbing species (e.g., HULIS); or (3) an absorbing core (e.g., soot or dust) coated with a non- or weakly absorbing species (e.g., condensed organics).^{49,51–61,65} These different aerosol microstructures are visualized in Fig. 1.

The ratio of the coating to core diameter in coated particles can also be an important factor. As shown in Fig. 2(b), two coated particles with the same external diameter but different core/coating diameter ratios will have different absorption and scattering characteristics. Thus, we conducted each experiment on coated particles twice, once with a constant core diameter and increasing shell thickness (see Fig. 2(b),i), and again with increasing core diameter whilst maintaining a constant shell thickness (see Fig. 2(b),ii).

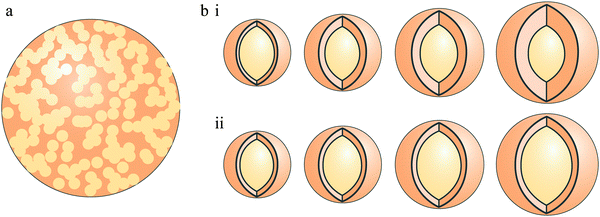Fig. 2 Internally mixed aerosols divided into homogeneously mixed aerosol (a) and heterogeneously mixed aerosols (coated particles) (b), with two types of coated aerosol, constant core diameter with increasing shell thickness (i), and increasing core diameter with constant shell thickness (ii).

It is of great interest to understand how these microstructures affect aerosol optical properties and how well theoretical calculations reproduce these characteristics in order to achieve more reliable climate model simulations. There are a number of approaches currently employed to calculate the radiative properties of internally mixed aerosols in climate models. For homogeneously internally mixed aerosols, effective medium approximations or “mixing rules” are often used to calculate the particles’ effective RI, and then a Mie scattering subroutine (for homogeneous spheres; described above) is applied to calculate the aerosol optical parameters. Mixing rules are derived assuming that pockets (“inclusions”) of an aerosol constituent(s) exist within a surrounding matrix comprised of another constituent(s). Each inclusion is subjected to a local quasi-steady electromagnetic field averaged over the configuration of all of the other inclusions, which contributes to a local polarizability. The local polarizabilities are summed to compute the macroscopic polarization of the entire aerosol, and the macroscopic polarization is related to the effective dielectric constant of the composite aerosol. (See Chýlek et al.^48,66 for more detail.) The combination of any mixing rule and a Mie scattering subroutine for homogeneous spheres implicitly assumes that either the constituents are truly homogeneously mixed or that at least one constituent is randomly distributed throughout a matrix comprised of the other constituents.

Examples of commonly used mixing rules include: (1) molar refraction and absorption, in which the effective molar refraction and effective molar absorption of the aerosol are calculated by linearly averaging the molar refractions and molar absorptions, respectively, of the RI of the aerosol matrix and inclusions, weighted by their molar fractions^38,67–69; (2) the “linear mixing rule”, in which the effective RI of the aerosol is calculated by linearly averaging the real and imaginary parts, respectively, of the aerosol matrix and inclusions, weighted by their volume fractions;⁴⁵ (3) the Maxwell–Garnett rule, according to which second-order effects due to neighboring inclusions are neglected, and the dielectric constant of the aerosol matrix without inclusions determines the local electromagnetic field that acts on the inclusions;^45,70 (4) the Bruggeman rule, according to which the aerosol matrix and inclusions act symmetrically on one another;^45,70 and (5) extended effective medium approximations, according to which terms of higher order than the electric dipole of the inclusions are included.^48,66,71,72

For coated particles, two approaches for calculating the radiative properties are common. For aerosols coated with water, a growth function—a parameterization describing the change in scattering coefficient as a function of relative humidity—is often used.^39,73 Alternatively, a Mie scattering subroutine for coated spheres can be used, which provides a more explicit calculation, whether the coating consists of water or of other aerosol constituents. Like Mie scattering subroutines for homogeneous spheres, Mie scattering subroutines for coated spheres give the scattering solution to Maxwell’s equations as a function of particle size and wavelength, but with extra boundary conditions at the interface between the two layers.^45,74,75 Since such subroutines are more computationally intensive than mixing rules or growth functions, they are often applied off-line in a look-up table fashion,⁷⁶ but they can also be applied on-line.⁶⁷

Only a few experimental studies of the optical properties of complex aerosols have so far been conducted.^{53,66,77–89} Here, we present new measurements of laboratory-generated aerosols and theoretical calculations of their optical properties, along with some of our previous studies of the optical properties of internally mixed and coated aerosols. With respect to homogeneously internally mixed aerosols, we consider three combinations: (1) a mixture of two non-absorbers, glutaric acid (an organic solid; Glu-A) and NaCl (an inorganic salt);⁸⁰ (2) AS (a non-absorbing salt) mixed with Suwannee River fulvic acid (a weakly-absorbing organic compound with optical properties similar to those of HULIS; SRFA);^27,90 and (3) AS mixed with Rhodamine-590 (a strong absorber in the visible range with an absorption peak around 532 nm wavelength; Rh-590).⁸⁰ Glu-A, NaCl, and AS are common components of tropospheric aerosols, while SRFA is a commonly-used proxy for HULIS.^27,90 With respect to coated aerosols, we consider three combinations: (1) Nigrosin (a strong absorber) coated with Glu-A (a non-absorbing organic solid); (2) polystyrene latex spheres (a non-absorbing solid; PSL) coated with Glu-A; and (3) PSL coated with β-carotene (a weakly absorbing organic compound; β-car). In addition, we present some thoughts about the possible implications of our results to atmospheric radiation balance and climate.

2. Methodology

Aerosols were generated by the methods illustrated in Fig. 3, described in detail in our previous publications.^{27,53,80,91,92} In short, an aqueous solution of the compound of interest is nebulized with dry and pure nitrogen, dried in a silica gel diffusion dryer, and charged by a neutralizer. Size selection of the resulting polydisperse aerosol is achieved with a differential mobility analyzer (DMA) (Fig. 3(a,b)), after which the nearly monodisperse aerosol flow is directed into a pulsed or continuous wave (CW) cavity ring down (CRD) system for optical measurements. These systems are described in the next section.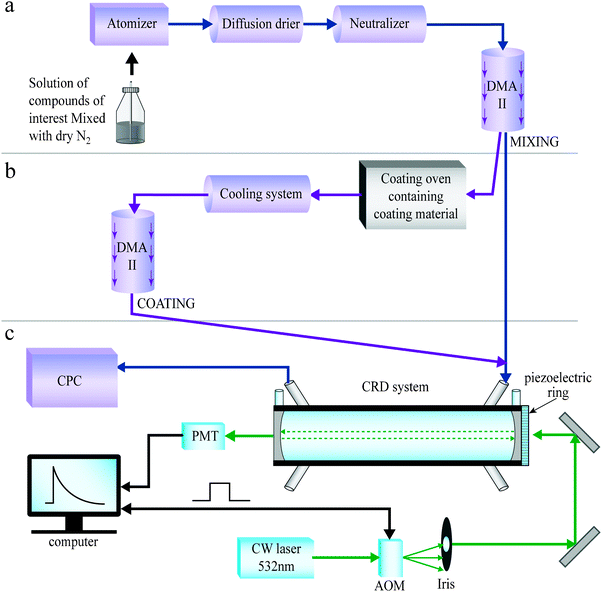

Fig. 3 Illustration of the setup for generating mixed (a) and coated (b) aerosols, coupled to the continuous wave (CW) cavity ring down (CRD) system (c).

Homogenously mixed particles are created by nebulizing aqueous mixtures, as shown in Fig. 3(a). Coated particles are created by using size-selected aerosols as seeds. The seeds are directed through a coating system, described in ref. 53 and illustrated in Fig. 3(b). In short, the coating material is placed in an oven in which the temperature and the flow rate control the coating thickness. After exiting the coating oven and cooling, the coated particles are size-selected in an additional DMA before entering the CRD system. The second size selection dictates the coating thickness that will be used. Aerosol sphericity was checked using atomic force microscopy in several cases.⁵³

CRD spectroscopy is a sensitive method for spectroscopy of gas phase species and for measuring optical properties of aerosols.^80,93–108 A pulsed or continuous laser beam enters a high finesse cavity, performing multiple reflections between two or three plano-concave mirrors.¹⁰⁶ The exponential decay time of the light exiting the cavity is measured, and differences in this time are related to the internal losses. The particles exiting the cavity are directed into a condensation optical counter (CPC) in order to measure the particle number concentration.

In a CRD aerosol spectrometer, scattering and absorption by the aerosol particles in the cavity lead to a reduction in the exponential decay time of the light compared to that in the empty cavity. From the reduction in decay time and the particle number concentration, the extinction efficiency (Q_ext) can be calculated for a specific wavelength and specific size parameter x (ratio between the particle diameter, D, and the laser wavelength, λ; x = πD/λ).^80,100,102

Several pulsed laser CRD systems covering several wavelength ranges were employed in this study.^53,80 Although pulsed systems often have lower sensitivities than CW systems, they can achieve quite reliable measurements. Their biggest advantage is their simplicity, making them easy to handle and operate.⁹¹

In addition to the pulsed laser systems, we use in this study a recently constructed CRD system employing a CW single mode laser operating at 532 nm (see Fig. 3(c)).⁹¹ In the portable system, an acousto-optic modulator (AOM) diffracts the 532 nm single mode laser beam, and the first order beam is directed into the cavity. The mirror at the light entrance side of the cavity is mounted on a piezoelectric ring that moves back and forth. This modifies the cavity’s length and hence its longitudinal modes. Once mode matching between the CW laser and the cavity is achieved, the light intensity in the cavity builds up. This triggers the AOM and the laser beam is deflected, leading to a single exponential decay of the light in the cavity which is detected by a photomultiplier (PMT) placed at one side of the cavity. The modulation frequency of the AOM is triggered by the light intensity in the PMT and is around 200 Hz. This new system improves the stability and sensitivity as compared to pulsed laser systems;^80,102 the sensitivity of our CW-CRD system was 6.64 × 10⁻¹⁰ cm⁻¹,⁹¹ compared to 3.77 × 10⁻⁹ cm⁻¹ in the pulsed CRD.⁸⁰ We present here experimental measurements obtained using both pulsed and CW laser systems.

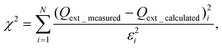
The complex RI of aerosols can be obtained using CRD measurements of the extinction efficiency as a function of particle size for a homogeneous spherical aerosol with the same composition throughout the size distribution. The retrieval algorithm compares the measured extinction efficiency as a function of the size parameter, with the extinction efficiency calculated using a Mie scattering subroutine for homogeneous spheres, while simultaneously varying the real and imaginary parts of the RI of the aerosols. The algorithm finds the complex RI of the aerosol particles by minimizing the “merit function”, χ²/N², where χ² is

N is the number of particle sizes, and ε_i is the standard deviation of the measurements of particle size i.^{27,48,53,80,91,102} The minimization is performed using the simplex search method¹⁰⁹ and can be performed to any desired resolution in RI values.

In addition to applying the retrieval algorithm to CRD measurements of single component spherical aerosols, the algorithm can essentially be applied to any aerosol configuration, with the Mie scattering subroutine for homogeneous spheres being replaced by some other appropriate theoretical calculation. For homogeneously internally mixed aerosols, a mixing rule computation can be inserted before the Mie scattering subroutine calculation, while for coated particles, a Mie scattering subroutine for coated spheres (“core/shell”) can be put in place of that for homogeneous spheres. Again, the complex RI of one or more of the aerosol constituents can be retrieved, or the merit function can be used simply to ascertain which theoretical approach best matches the measurements for a given set of (known) RI.⁸⁰

3. Laboratory measurements of complex aerosols

Homogeneously internally mixed aerosols

The Q_ext of laboratory-generated aerosols comprised of internal mixtures of NaCl and Glu-A with molar ratios 1 : 1 and 1 : 2 was measured in ref. 80 with a pulsed CRD aerosol spectrometer employing a 532 nm Nd : YAG laser. These homogeneously internally mixed aerosols mimic aerosols comprised of inorganic and organic mixtures often detected above urban and polluted areas.²² The aerosol RI retrieval algorithm was then used to test which mixing rule provides the best match to the measurements, given values of the RI of the pure constituents that make up the mixture as retrieved using the same system (RI = 1.546 + i0.003 for pure NaCl and RI = 1.41 + i0.00 for pure Glu-A). The level of agreement between the mixing rules and the experimental data was determined using the merit function (eqn (1)); the smaller the merit function, the better the agreement. The results are shown in Fig. 4. The linear mixing rule provides the best match to the experimental Q_ext values; for a 1 : 1 mixture of Glu-A and NaCl, the merit function value for the linear mixing rule is 0.14 as compared to 0.15–2.65 for the other mixing rules, and for a 1 : 2 mixture of of Glu-A and NaCl, the merit function value for the linear mixing rule is 0.14 as compared to 0.14–2.80 for the other mixing rules, when all particle sizes are included.⁸⁰ We surmise that the high solubility of both compounds in the aqueous solution ensured thorough mixing. This, combined with the fact that the two constituents exhibit very little absorption, allows such good agreement with the simple linear mixing rule.

Fig. 4 Extinction efficiency of mixed particles of NaCl and Glutaric acid (Glu-A) in mass ratios 1 : 1 and 1 : 2, respectively, along with the Mie curves corresponding to the effective refractive indices calculated with the volume-weighted “linear mixing” rule at 532 nm wavelength.

In a new set of mixing experiment, the Q_ext of aerosols comprised of internal mixtures of AS (non-absorbing) and SRFA (weakly absorbing material) with molar ratio 1 : 1 was measured using an optical parametric oscillator (OPO) pulsed laser system at 390 nm wavelength. These homogeneously internally mixed aerosols again mimic aerosols comprised of inorganic and organic mixtures often detected in urban and polluted areas.²² The wavelength 390 nm was chosen for several reasons. First, SRFA absorbs better at shorter wavelengths than at 532 nm, as implicit in the imaginary part of its RI (RI = 1.602 + i0.098 at 390 nm, while RI = 1.634 + i0.004 at 532 nm).²⁷ Second, near ultraviolet wavelengths are often employed in satellite measurements of aerosol absorption.¹¹⁰

The mixed aerosol RI retrieval algorithm was then used to test which mixing rule provides the best match to the measurements, given values of the RI of the pure constituents that make up the mixture, which were previously retrieved using the same system (RI = 1.525 + i0.0008 for pure AS and RI = 1.602 + i0.098 for pure SRFA). The results are shown in Fig. 5. The linear mixing rule provides the best match to the experimental Q_ext values, but all of the mixing rules tested provide reasonable results; for a 1 : 1 mixture of AS and SRFA, the merit function value for the linear mixing rule is 0.11 as compared to 0.11–0.18 for the other mixing rules. We conclude that for homogeneous internal mixtures of non-absorbing and weakly absorbing constituents, Q_ext is not overly sensitive to how the interaction between the electromagnetic fields of the constituents is described.

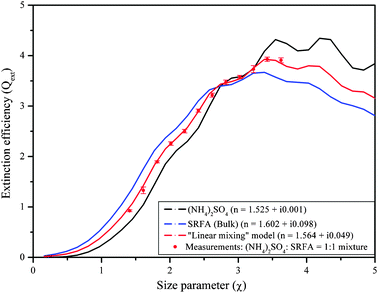Fig. 5 Extinction efficiency of mixed ammonium sulfate (AS) and Suwannee River fulvic acid (SRFA) particles with a 1 : 1 mass ratio, along with the Mie curves corresponding to the effective refractive indices calculated with the volume–weighted “linear mixing” rule at 390 nm wavelength.

However, when one of the constituents in the homogeneous internal mixture is strongly absorbing, the situation changes. In ref. 80 the Q_ext of laboratory-generated aerosols comprised of internal mixtures of AS and Rh-590 was also measured with the Nd : YAG pulsed CRD aerosol spectrometer running at 532 nm wavelength. Due to the low solubility of Rh-590 in water, the aqueous solution of the mixture was diluted with 10% ethanol. The aerosol RI retrieval algorithm was then used to test which mixing rule provides the best match to the measurements. We found that for low volume fractions of Rh-590, the Mie scattering subroutine for coated spheres, rather than one of the mixing rules, provides the best agreement with measurements; for a 1 : 500 mixture of Rh-590 and AS, the merit function value for the Mie scattering subroutine for coated spheres, including particle sizes starting from 350 nm, is 3.29 as compared to 3.90–4.26 for the mixing rules. The lack of success of the mixing rules for low volume fractions of the strong absorber could be attributed to residue of ethanol, which, unlike water, may not have completely evaporated in the diffusion drier. Additionally, AS has a different solubility in water than Rh-590, which might have caused the final molar ratios of the two constituents to differ from their original molar ratios in the solution or might have led to the formation of a more heterogeneous internal mixture akin to a coated particle. Alternatively, the coated sphere model might better represent the interaction between the electromagnetic fields of the constituents in the case of a strong absorber with low volume fraction even if they are truly homogeneously mixed. For higher volume fractions of Rh-590 in the mixture, we found that the extended effective medium approximation provides the best agreement with measurements; for a 1 : 10 mixture of Rh-590 and AS, the merit function value for the extended effective medium approximation, including particle sizes from 350 nm and inclusion size 10 nm, is 2.95 as compared to 5.85–9.57 for the other mixing rules and as compared to 31.72 for the Mie scattering subroutine for coated spheres. The success of the extended effective medium approximation for high volume fractions of the strong absorber is likely connected to the fact that, among all of the mixing rules, the extended effective medium approximation retains the highest order representation of the electromagnetic fields, allowing the highest order description of the interaction between internal scattering and absorption.

In addition to testing the theoretical calculation approaches against extinction measurements, we also performed calculations of the single scattering albedo (see section 1; ϖ) and the direct radiative forcing efficiency (RFE; the difference in radiative flux at the top of the atmosphere with and without aerosols per unit optical depth) for a pollution-type aerosol containing ammonium sulfate, absorbing organic carbon (HULIS), and soot.²⁷ Our calculations suggest that accounting for absorption by HULIS leads to a significant decrease in ϖ (more atmospheric absorption) and to a significant increase in aerosol RFE (heating) as compared to pollution-type aerosols containing only non-absorbing organic aerosol constituents. Therefore, an additional conclusion is that HULIS and similarly absorbing organic constituents are important contributors to the radiative balance in the atmosphere and to the climate in polluted environments.

Heterogeneously mixed (coated) aerosols

In ref. 53, measurements of the Q_ext of laboratory-generated aerosols comprised of Nigrosin coated with Glu-A performed with the Nd : YAG pulsed CRD at 532 nm wavelength were reported. The aerosol retrieval algorithm was then used to test the accuracy of the Mie scattering subroutine for coated spheres, and the results are shown in Fig. 6. As can be seen, the Mie scattering subroutine is successful at predicting the aerosol Q_ext for thin coatings (constant shell thickness of 20 nm; compare the green curve to the green dots). However, it is less successful at predicting the aerosol Q_ext for thicker coatings (increasing shell thickness; compare the blue curve to the blue dots), with the Mie calculation over-predicting the extinction by a greater extent as the shell thickness increases. The same discrepancy occurred when the coating was switched to diethyl-hexyl-sebacate (a non-absorbing organic liquid; DEHS⁵³), which is liquid at room temperature rather than solid like Glu-A. In ref. 53, we suggested that these discrepancies result from either a lack of perfect sphericity in the generated aerosols or from changes in the dielectric constant of the coating near the interface between the core and coating. However, no theoretical representations of such physical effects that we tested completely resolved the discrepancy. Since then, we have conducted further sensitivity tests, systematically reducing the RI of the coating in the theoretical calculations. A reduction in RI corresponding to a mixture of air with Glu-A with mass ratio 1 : 5 (representing, for example, pockets of air in the coating) calculated with the linear mixing rule does bring the calculations more in line with the measured extinction. Although Guenther (1984)¹¹¹ did suggest that small distortions can occur at the interface between the surface of the core and coating when physical vapor deposition is used to generate the coating, and that these distortions can develop into narrow air pockets, we have no evidence that such pockets exist in our coatings. The mechanism by which Glu-A vapors condense onto the core particle in the coating oven needs to be examined more thoroughly.

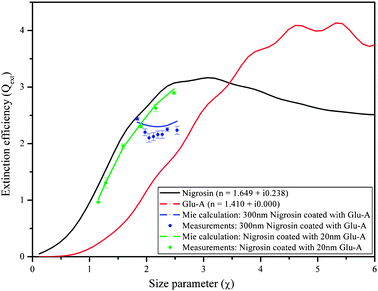Fig. 6 Extinction efficiency of Nigrosin coated with glutaric acid (Glu-A), along with the Mie curves for coated spheres at 532 nm wavelength. Blue curve and symbols: constant core diameter with increasing shell thickness; green curve and symbols: increasing core diameter with constant shell thickness.

To investigate whether coated particles presenting different optical properties exhibit the same discrepancy, we present new measurements of Q_ext of laboratory-generated aerosols comprised of PSL coated with Glu-A recently measured with the new CW-CRD system at 532 nm wavelength. The results are compared with calculations using the same Mie scattering subroutine for coated spheres, as shown in Fig. 7. As can be seen, the Mie scattering subroutine is successful at predicting the aerosol extinction for both thin coatings (constant shell thickness of 40 nm; compare the green curve to the green dots) and thicker coatings (increasing shell thickness; compare the blue curve to the blue dots). Although surface (interface) effects should be more stable in the case of Nigrosin coated by Glu-A (due to hydrogen bonds, compared to mostly van der Waals in the case of PSL coated by Glu-A), we found that PSL coated by Glu-A can be well described by the core plus shell model. A possible explanation for these results might be the existence of a mixed layer in the interface between the Nigrosin core and the Glu-A shell. In this case, a different model needs to be applied, and again, a more thorough investigation on the mechanism by which Glu-A vapors condense onto the core particle in the coating oven is needed.

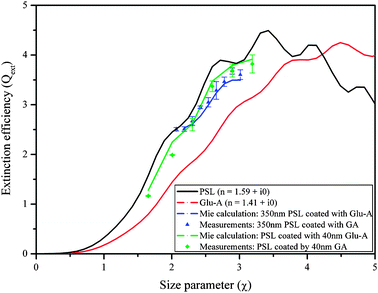Fig. 7 Extinction efficiency of PSL coated with glutaric acid (Glu-A), along with the Mie curves for coated spheres at 532 nm wavelength. Blue curve and symbols: constant core diameter with increasing shell thickness; green curve and symbols: increasing core diameter with constant shell thickness. The red and black lines are Mie fits for measured points using the same system. The green and blue lines are the results of the coated sphere Mie calculation, using the retrieved RIs as input parameters.

In the next experiment, non-absorbing particles with a weakly absorbing coating were examined. β-Carotene was chosen as the coating material because it is more stable at high temperatures than other absorbers such as Nigrosin. The Q_ext of laboratory-generated aerosols comprised of PSL coated with β-car was measured with the new CW-CRD system at 532 nm wavelength, and the aerosol RI retrieval algorithm was used to retrieve the RI of β-car, given the previously retrieved/known RI for PSL (RI = 1.590 + i0.000). The retrieved value for β-car is RI = 1.455 + i0.090, with a merit value of 2.38. To the best of our knowledge, the RI of β-car at 532 nm has not previously been reported in the literature. The real part of the retrieved RI is in good agreement with values for typical organic compounds (∼1.4), while the imaginary part was validated by measuring the absorption of β-car dissolved in dichloromethane (CH₂Cl₂) with a spectrophotometer (CARY 100 Bio UV-Visible spectrophotometer, Varian). The imaginary part of the RI of β-car derived from the spectrophotometer measurements according to the formulation in Jacobson et al.¹¹² is 0.075 ± 0.001, a difference of 0.025 from our retrieved value. This difference, though not very large, may be inherent in the different methods of measurement or could be caused by interactions of dissolved β-car with the solvent. Either way, we take the retrieved value of 0.090 to be reliable.

The results of the measurements for PSL coated with β-car are shown in Fig. 8. As can be seen, there are differences between the measurements and the calculated extinction (calculated using the retrieved RI for β-carotene and the Mie scattering subroutine for coated spheres) that increase with increasing particle size. However, the differences are not systematic; at times, the theoretical calculations over-predict the extinction, and at other times they under-predict the extinction. This is true for the experiment with constant shell thickness of 40 nm (compare the green curve to the green dots and see Table 1; the differences are up to 10%) and for the experiment with increasing shell thickness (compare the blue curve to the blue dots). The differences between the measurements and the calculated extinction in the case of PSL coated with β-car as compared to PSL coated with Glu-A may result from the more rigid molecular structure of β-car, leading to a less organized shell around the core PSL.

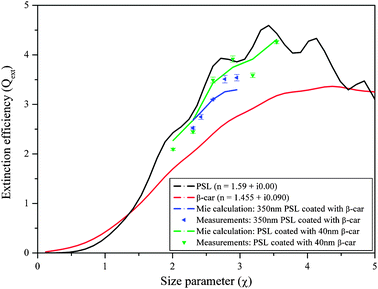Fig. 8 Extinction efficiency of PSL coated with β-carotene (β-car), along with the Mie curves for coated spheres at 532 nm wavelength. Blue curve and symbols: constant core diameter with increasing shell thickness; green curve and symbols: increasing core diameter with constant shell thickness.

Table 1 Percentage error between the measured and calculated Q_ext for PSL coated with glutaric-acid (Glu-A) and with β-carotene (β-car) in both models (constant core diameter with increasing shell thickness and increasing core diameter with constant shell thickness)

Coated diameter/nm	Size parameter (x)	Q ext calculated	Q ext measured	Error/%
PSL–Glu-A: const. core diameter (350 nm)
350	2.067	2.510	2.506	0.143
370	2.185	2.532	2.511	0.821
390	2.303	2.616	2.672	2.170
410	2.421	2.768	2.949	6.510
430	2.539	2.992	3.050	1.916
450	2.657	3.239	3.288	1.531
470	2.775	3.421	3.463	1.223
490	2.894	3.495	3.679	5.253
510	3.012	3.494	3.605	3.197
PSL–Glu-A: const. shell thickness (40 nm)
280	1.653	1.279	1.165	8.860
340	2.008	2.250	1.989	11.593
390	2.303	2.616	2.601	0.573
440	2.598	3.475	3.371	2.971
490	2.894	3.794	3.689	2.767
540	3.189	3.916	3.821	2.426
PSL–β-car: const. core diameter (350 nm)
390	2.303	2.681	2.523	5.875
410	2.421	2.843	2.747	3.359
440	2.598	3.100	3.102	0.048
470	2.775	3.255	3.510	7.837
500	2.953	3.296	3.539	7.376
PSL–β-car: const. shell thickness (40 nm)
340	2.008	2.270	2.094	7.775
390	2.303	2.681	2.445	8.807
440	2.598	3.430	3.492	1.796
490	2.894	3.750	3.917	4.440
540	3.189	3.914	3.587	8.335
600	3.543	4.309	4.258	1.167

---

4. Conclusions

We have summarized and reviewed experiments and theoretical calculations of optical properties of complex aerosols. Specifically, we focused on the impact of aerosol microstructure on the effective refractive index of aerosols composed of internal mixtures of components with different optical properties. In the atmosphere, most aerosols are multi-component, and therefore detailed understanding and modeling of their complex refractive index will reduce the uncertainty related to energy balance and climate change modeling.

By controlling the aerosol microstructure and the mass ratios of the components and knowing the RI of one or more of the separate components that make up the aerosols at the wavelength of interest, through our experiments we were able to validate different theoretical approaches used for evaluating the optical properties of complex aerosols. Our approach also allowed us to retrieve the aerosol’s Q_ext and/or the RI of one or more of the components.

We conclude that the effective RI of homogeneously mixed aerosols comprised of two non-absorbing materials with similar water solubilities can be accurately calculated with the simple mass or concentration based “linear mixing” rule. In the case of a non-absorbing material homogeneously mixed with weakly absorbing compounds, we conclude that all mixing rules provide a reasonable estimate, but the coated sphere Mie calculation does not always perform as well. In the case of a strong absorber “homogeneously” mixed with a non-absorber (with different solubilities in water), the success of the different theoretical approaches varies with the mass fraction of the absorber. For low absorber mass fractions, surprisingly, the coated sphere Mie calculation provides the best estimate, while for high absorber mass fractions, the extended effective medium approximation provides the best estimate. Given the above, we conclude that the microstructure is actually dissimilar for high and low mass fractions of the absorbing compound. In order to generalize this statement for other absorbers, we first need to eliminate the influence of the solubility difference on the results.

Regarding coated particles, we find that the coated sphere Mie subroutine gives an accurate calculation of Q_ext for aerosols comprised of a non-absorber coated by another non-absorber. However, for aerosols comprised of a strong absorber coated by a non-absorber or of a non-absorber coated by a weak absorber, discrepancies of up to 10% between the measurements and theoretical calculations were documented. These discrepancies await further investigation with more advanced instrumentation in order to understand their origin. Several such tools can be considered. Multiwavelength CRD could provide a comprehensive view of the wavelength dependence of the refractive index for the internally mixed particles. Measuring the absorption coefficient with a photo-acoustic spectrophotometer (PAS) coupled to the CRD system could provide direct and independent measurements of the extinction and absorption of aerosols and hence direct measurement of the single scattering albedo of the aerosol and more accurate values of the imaginary part of the complex index of refraction. A new approach, that was recently developed by Thompson et al., is the albedometer.¹¹³ This instrument combines CRD within an integrating sphere nephelometer. The CRD resonator was built using the integrating sphere by mounting the CRD mirrors on opposite sides of the sphere. The light scattered by the aerosols inside the sphere is collected by the inner side of the sphere to a separate PMT from the CRD PMT. The main advantage of this method is the simultaneous determination of the extinction and scattering in a single instrument utilizing two very sensitive methods. In addition, combining the methods in a single instrument would minimize the errors in the measurements due to different sample conditions in different instruments.

Acknowledgements

This work was partially supported by the Israel Science Foundation (grants 1527/07 and 196/08). Y.R. acknowledges financial support by the Helen and Martin Kimmel Award for Innovative Investigation. We thank H. E. Levy for programming support, and A. Moroz and M. Tzemach for helpful suggestions regarding surface/interface effects in coated particles.

References

1. B. J. Finlayson-Pitts and J. Pitts, Jr., Chemistry of the Upper and Lower Atmosphere, Academic Press, CA, 1999.
2. J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics, 2nd edn, John Wiley & Sons Inc, 2006.
3. P. U. Poschl, Angew. Chem., Int. Ed., 2005, 44, 7520.
4. Y. Rudich, N. M. Donahue and T. F. Mentel, Annu. Rev. Phys. Chem., 2007, 58, 321–352.
5. M. C. Jacobson, H. C. Hansson, K. J. Noone and R. Charlson, Rev. Geophys., 2000, 38, 267–294.
6. Y. Rudich, Chem. Rev., 2003, 103, 5097–5124.
7. M. Kulmala, H. Vehkamaki, T. Petaja, M. Dal Maso, A. Lauri, V. M. Kerminen, W. Birmili and P. H. McMurry, J. Aerosol Sci., 2004, 35, 143–176.
8. B. T. Johnson, K. P. Shine and P. M. Forster, Q. J. R. Meteorol. Soc., 2004, 130, 1407–1422.
9. U. Lohmann and J. Feichter, Geophys. Res. Lett., 2001, 28, 159.
10. S. Menon, J. Hansen, L. Nazarenko and Y. Luo, Science, 2002, 297, 2250–2253.
11. U. Lohmann and J. Feichter, Atmos. Chem. Phys., 2005, 5, 715.
12. D. Y. Kim and V. Ramanathan, J. Geophys. Res.-Atmos., 2008, 113.
13. S. Solomon, D. Qin, M. Manning, R. B. Alley, T. Berntsen, N. L. Bindoff, Z. Chen, A. Chidthaisong, J. M. Gregory, G. C. Hegerl, M. Heimann, B. Hewitson, B. J. Hoskins, F. Joos, J. Jouzel, V. Kattsov, U. Lohmann, T. Matsuno, M. Molina, N. Nicholls, J. Overpeck, G. Raga, V. Ramaswamy, J. Ren, M. Rusticucci, R. Somerville, T. F. Stocker, P. Whetton, R. A. Wood and D. Wratt, Technical Summary, in Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, 2007.
14. Y. J. Kaufman, I. Koren, L. A. Remer, D. Rosenfeld and Y. Rudich, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11207–11212.
15. V. Ramanathan, C. Chung, D. Kim, T. Bettge, L. Buja, J. T. Kiehl, W. M. Washington, Q. Fu, D. R. Sikka and M. Wild, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 5326–5333.
16. Y. J. Kaufman and I. Koren, Science, 2006, 313, 655–658.
17. I. Koren, L. A. Remer, Y. J. Kaufman, Y. Rudich and J. V. Martins, Geophys. Res. Lett., 2007, 34.
18. I. Koren, J. V. Martins, L. A. Remer and H. Afargan, Science, 2008, 321, 946–949.
19. D. Rosenfeld, U. Lohmann, G. B. Raga, C. D. O’Dowd, M. Kulmala, S. Fuzzi, A. Reissell and M. O. Andreae, Science, 2008, 321, 1309–1313.
20. H. Moosmuller, R. K. Chakrabarty and W. P. Arnott, J. Quant. Spectrosc. Radiat. Transfer, 2009, 110, 844–878.
21. C. Erlick, V. Ramaswamy and L. M. Russell, J. Geophys. Res., 2006, 111, D06204.
22. Q. Zhang, J. L. Jimenez, M. R. Canagaratna, J. D. Allan, H. Coe, I. Ulbrich, M. R. Alfarra, A. Takami, A. M. Middlebrook, Y. L. Sun, K. Dzepina, E. Dunlea, K. Docherty, P. F. DeCarlo, D. Salcedo, T. Onasch, J. T. Jayne, T. Miyoshi, A. Shimono, S. Hatakeyama, N. Takegawa, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, P. Williams, K. Bower, R. Bahreini, L. Cottrell, R. J. Griffin, J. Rautiainen, J. Y. Sun, Y. M. Zhang and D. R. Worsnop, Geophys. Res. Lett., 2007, 34.
23. K. Chamaillard, S. G. Jennings, C. Kleefeld, D. Ceburnis and Y. J. Yoon, J. Quant. Spectrosc. Radiat. Transfer, 2003, 79–80, 577–597.
24. J. T. Kiehl, T. L. Schneider, P. J. Rasch and M. C. Barth, J. Geophys. Res., 2000, 105, 1441–1457.
25. C. E. Lund Myhre and C. J. Nielsen, Atmos. Chem. Phys. Discuss., 2004, 4, 3013.
26. S. F. Maria, L. M. Russell, M. K. Gilles and S. C. B. Myneni, Science, 2004, 306, 1921–1924.
27. E. Dinar, A. A. Riziq, C. Spindler, C. Erlick, G. Kiss and Y. Rudich, Faraday Discuss., 2008, 137, 279–295.
28. M. O. Andreae, Nature, 2001, 409, 671–672.
29. T. C. Bond, D. G. Streets, K. F. Yarber, S. M. Nelson, J. H. Woo and Z. Klimont, J. Geophys. Res., 2004, 109, D14203.
30. B. F. Henson, J. Geophys. Res., 2007, 112, D24S16.
31. L. Liua and M. I. Mishchenkoa, J. Quant. Spectrosc. Radiat. Transfer, 2007, 106, 262–273.
32. Z. Li, P. Goloub, L. Blarel, B. Damiri, T. Podvin and I. Jankowiak, Appl. Opt., 2007, 46, 1548–1553.
33. I. N. Sokolik and O. B. Toon, Nature, 1996, 381, 681–683.
34. M. O. Andreae and A. Gelencser, Atmos. Chem.Phys. Discuss., 2006, 6, 3419–3463.
35. S. F. S. Decesari, M. C. Facchini, M. Mircea, L. Emblico, F. Cavalli, W. Maenhaut, X. Chi, G. Schkolnik, A. Falkovich, Y. Rudich, M. Claeys, V. Pashynska, G. Vas, I. Kourtchev, R. Vermeylen, A. Hoffer, M. O. Andreae, E. Tagliavini, F. Moretti and P. Artaxo, Atmos. Chem. Phys., 2006, 6, 375.
36. A. Hoffer, A. Gelencser, P. Guyon, G. Kiss, O. Schmid, G. P. Frank, P. Artaxo and M. O. Andreae, Atmos. Chem. Phys., 2006, 6, 3563–3570.
37. H. L. Sun, L. Biedermann and T. C. Bond, Geophys. Res. Lett., 2007, 34.
38. M. Born and E. Wolf, Principles of optics, 7th edn, Cambridge University Press, 1999.
39. T. S. Bates, T. L. Anderson, T. Baynard, T. Bond, O. Boucher, G. Carmichael, A. Clarke, C. Erlick, H. Guo, L. Horowitz, S. Howell, S. Kulkarni, H. Maring, A. McComiskey, A. Middlebrook, K. Noone, C. D. O’Dowd, J. Ogren, J. Penner, P. K. Quinn, A. R. Ravishankara, D. L. Savoie, S. E. Schwartz, Y. Shinozuka, Y. Tang, R. J. Weber and Y. Wu, Atmos. Chem. Phys., 2006, 6, 1657–1732.
40. N. Bellouin, O. Boucher, J. Haywood and M. S. Reddy, Nature, 2005, 438, 1138–1141.
41. W.-T. Chen, R. A. Kahn, D. Nelson, K. Yau and J. H. Seinfeld, J. Geophys. Res., 2008, 113.
42. Y. J. Kaufman, Nature, 2002, 419, 215.
43. Y. J. Kaufman and R. S. Fraser, Science, 1997, 277, 1636–1639.
44. G. W. Petty, A First Course in Atmospheric Radiation, Sundog publishing, Madison, Wisconsin, 2004.
45. C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York, 1983.
46. G.-h. Dai, Z.-b. Ren, Q. Sun and J. Liu, Proc. SPIE–Int. Soc. Opt. Eng., 2006, 602723.
47. G. Mie, Ann. Phys., 1908, 25, 377–445.
48. C. Erlick, J. Atmos. Sci., 2006, 63, 754–763.
49. G. Lesins, P. Chylek and U. Lohmann, J. Geophys. Res., 2002, 107, 4094.
50. C. Marcolli, B. P. Luo, T. Peter and F. G. Wienhold, Atmos. Chem. Phys., 2004, 4, 2593–2599.
51. F. Parungo, in Atmos. Aerosol. Nucleat., 1988, p. 269.
52. F. P. Parungo, C. T. Nagamoto, J. Rosinski and P. L. Haagenson, J. Atmos. Chem., 1986, 4, 199.
53. A. A. Riziq, M. Trainic, C. Erlick, E. Segre and Y. Rudich, Atmos. Chem. Phys., 2008, 8, 1823–1833.
54. A. H. Falkovich, G. Schkolnik, E. Ganor and Y. Rudich, J. Geophys. Res., 2004, 109, D02208.
55. S. A. Guazzotti, J. R. Whiteaker, D. Suess, K. R. Coffee and K. A. Prather, Atmos. Environ., 2001, 35, 3229.
56. Q. Zhang, M. R. Canagaratna, J. T. Jayne, D. R. Worsnop and J. L. Jimenez, J. Geophys. Res.-Atmos., 2005, 110.
57. G. B. Ellison, A. F. Tuck and V. Vaida, J. Geophys. Res., 1999, 104, 11633–11641.
58. V. Vaida, A. F. Tuck and G. B. Ellison, Phys. Chem. Earth Pt. C-Solar-Terr. Planet. Sci., 2000, 25, 195–198.
59. A. Laskin, D. J. Gaspar, W. H. Wang, S. W. Hunt, J. P. Cowin, S. D. Colson and B. J. Finlayson-Pitts, Science, 2003, 301, 340–344.
60. V. H. Grassian, Int. Rev. Phys. Chem., 2001, 20, 467–548.
61. M. Posfai, J. R. Anderson, P. R. Buseck and H. Sievering, J. Geophys. Res., 1999, 104, 21685–21693.
62. K. Karar, A. Gupta, A. Kumar and A. Biswas, Environ. Monit. Assess., 2006, 120, 347.
63. U. Panne, R. E. Neuhauser, M. Theisen, H. Fink and R. Niessner, Spectrochim. Acta, Part B, 2001, 56, 839.
64. M. H. Shah, N. Shaheen and M. Jaffar, J. Chem. Soc. Pak., 2007, 29, 598–604.
65. H. X. Xue, A. F. Khalizov, L. Wang, J. Zheng and R. Y. Zhang, Environ. Sci. Technol., 2009, 43, 2787–2792.
66. P. Chylek, G. Videen, D. J. W. Geldart, J. S. Dobbie and H. C. W. Tso, Effective medium approximations for heterogeneous particles in: Light scattering by nonspherical particles, theory, measurements and application, Academic Press, 2000.
67. M. Z. Jacobson, J. Geophys. Res., 2002, 107.
68. A. W. Stelson, Environ. Sci. Technol., 1990, 24, 1676–1679.
69. I. N. Tang, J. Geophys. Res., 1997, 102.
70. P. Chylek, V. Ramaswamy and R. J. Cheng, J. Atmos. Sci., 1984, 41, 3076–3084.
71. A. Sihvola and R. Sharma, Microwave Opt. Technol. Lett., 1999, 22, 229–231.
72. M. Z. Jacobson, J. Phys. Chem. A, 2006, 110, 6860–6873.
73. M. R. Beaver, R. M. Garland, C. A. Hasenkopf, T. Baynard, A. R. Ravishankara and M. A. Tolbert, Environ. Res. Lett., 2008, 3, 045003.
74. R. E. Danielson, D. R. Moore and H. C. van de Hulst, J. Atmos. Sci., 1969, 26, 1078–1087.
75. T. P. Ackerman and O. B. Toon, Appl. Opt., 1981, 20, 3661–3667.
76. J. E. Penner, C. C. Chuang and K. Grant, Clim. Dyn., 1998, 14, 839.
77. O. Mohler, S. Benz, H. Saathoff, M. Schnaiter, R. Wagner, J. Schneider, S. Walter, V. Ebert and S. Wagner, Environ. Res. Lett., 2008, 3, 025007.
78. O. Mohler, S. Buttner, C. Linke, M. Schnaiter, H. Saathoff, O. Stetzer, R. Wagner, M. Kramer, A. Mangold, V. Ebert and U. Schurath, J. Geophys. Res., 2005, 110, D11210.
79. M. Schnaiter, C. Linke, O. Mohler, K. H. Naumann, H. Saathoff, R. Wagner, U. Schurath and B. Wehner, J. Geophys. Res., 2005, 110, D19204.
80. A. A. Riziq, C. Erlick, E. Dinar and Y. Rudich, Atmos. Chem. Phys., 2007, 7, 1523–1536.
81. K. Adachi and P. R. Buseck, Atmos. Chem. Phys., 2008, 8, 6469–6481.
82. P. J. Sheridan, W. P. Arnott, J. A. Ogren, E. Andrews, D. B. Atkinson, D. S. Covert, H. Moosmuller, A. Petzold, B. Schmid, A. W. Strawa, R. Varma and A. Virkkula, Aerosol Sci. Technol., 2005, 39, 1–16.
83. A. F. Khalizov, H. Xue, L. Wang, J. Zheng and R. Zhang, J. Phys. Chem. A, 2009, 113, 1066–1074.
84. P. Chylek, V. Srivastava, R. G. Pinnick and R. T. Wang, Appl. Opt., 1988, 27, 2396.
85. G. Videen, D. Ngo and P. Chlek, Opt. Lett., 1994, 19, 1675.
86. G. Videen and P. Chlek, Opt. Commun., 1998, 158, 1.
87. M. J. Wolff, G. C. Clayton and S. J. Gibson, Astrophys. J., 1998, 503, 815–830.
88. J. E. Spanier and I. P. Herman, Phys. Rev. B., 2000, 61, 10437.
89. L. Kolokolova and B. S. Gustafsonm, J. Quant. Spectrosc. Radiat. Transfer, 2001, 70, 611.
90. E. R. Graber and Y. Rudich, Atmos. Chem. Phys. Discuss., 2006, 5, 9801.
91. N. Lang-Yona, Y. Rudich, E. Segre, E. Dinar and A. Abo-Riziq, Anal. Chem., 2009, 81, 1762–1769.
92. C. Spindler, A. Abo Riziq and Y. Rudich, Aerosol Sci. Technol., 2007, 41, 1011–1017.
93. A. O. Keefe and D. A. G. Deacon, Rev. Sci. Instrum., 1988, 59, 2544–2555.
94. D. Romanini, A. A. Kachanov, N. Sadeghi and F. Stoeckel, Chem. Phys. Lett., 1997, 264, 316–322.
95. M. D. Wheeler, S. M. Newman and A. J. Orr-Ewing, J. Chem. Phys., 1998, 108, 6594–6605.
96. S. S. Brown, H. Stark, S. J. Ciciora, R. J. McLaughlin and A. R. Ravishankara, Rev. Sci. Instrum., 2002, 73, 3291–3301.
97. M. Mazurenka, A. J. Orr-Ewing, R. Peverallb and and G. A. D. Ritchieb, Annu. Rep. Prog. Chem., Sect. C, 2005, 101, 100–142.
98. M. Pradhan, R. E. Lindley, R. Grilli, I. R. White, D. Martin and A. J. Orr-Ewing, Appl. Phys. B, 2008, 90, 1–9.
99. G. Berden, R. Peeters and G. Meijer, Int. Rev. Phys. Chem., 2000, 19, 565.
100. V. Bulatov, M. Fisher and I. Schechter, Anal. Chim. Acta, 2002, 466, 1–9.
101. H. Moosmuller, R. Varma and W. P. Arnott, Aerosol Sci. Technol., 2005, 39, 30–39.
102. A. Pettersson, E. R. Lovejoy, C. A. Brock, S. S. Brown and A. R. Ravishankara, J. Aerosol Sci., 2004, 35, 995–1011.
103. A. D. Sappey, E. S. Hill, T. Settersten and M. A. Linne, Opt. Lett., 1998, 23, 954–956.
104. J. D. Smith and D. B. Atkinson, Analyst, 2001, 126, 1216–1220.
105. A. W. Strawa, R. Castaneda, T. Owano, D. S. Baer and B. A. Paldus, J. Atmos. Oceanic Technol., 2003, 20, 454–465.
106. T. J. A. Butler, J. L. Miller and A. J. Orr-Ewing, J. Chem. Phys., 2007, 126, 174302.
107. J. J. Scherer, J. B. Paul, A. O’Keefe and R. J. Saykally, Chem. Rev., 1997, 97, 25–52.
108. S. M. Ball and R. L. Jones, Chem. Rev., 2003, 103, 5239–5262.
109. J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, SIAM J. Optim., 1998, 9, 112–147.
110. O. Torres, A. Tanskanen, B. Veihelmann, C. Ahn, R. Braak, P. K. Bhartia, P. Veefkind and P. Levelt, J. Geophys. Res., 2007, 112, D24S47.
111. K. H. Guenther, Appl. Opt., 1984, 23, 3806.
112. M. Z. Jacobson, J. Geophys. Res., 1999, 104, 3527–3542.
113. J. E. Thompson, N. Barta, D. Policarpio and R. DuVall, Opt. Express, 2008, 16, 2191–2205.

---