Nanoparticle stability from the nano to the meso interval
Alvaro
Mayoral
,
Hector
Barron
,
Ruben
Estrada-Salas
,
Alma
Vazquez-Duran
and
Miguel
José-Yacamán
*
Department of Physics and Astronomy, The University of Texas at San Antonio, One UTSA Circle, San Antonio, TX 78249, USA. E-mail: miguel.yacaman@utsa.edu; Fax: (+210) 458-4919; Tel: +210-458-6954
First published on 7th December 2009
Abstract
Nanoparticles are the cornerstone of nanotechnology. Their crystal structure and relation to shape are still open problems despite a lot of advances in the field. The classical theory of nanoparticle stability predicts that for sizes <1.5–2 nm the icosahedral structure should be the most stable, then between around 2–5 nm, the decahedral shape should be the most stable. Beyond that, face-centered-cubic (FCC) structures will be the predominant phase. However, in the experimental side, icosahedral (Ih) and decahedral (Dh) particles can be observed much beyond the 5 nm limit. In fact, it is possible to find Ih and Dh particles even in the mesoscopic range. Conversely, it is possible to find FCC particles with a size <1.5 nm. In this paper we review a number of the mechanisms proposed in the literature that allow the stabilization of nanoparticles. Some of the mechanisms are very interrelated and it becomes difficult to distinguish between them.
Introduction
Crystals have attracted the attention of mankind since prehistoric times. Driven by an interest in ornaments, technology for cutting crystals was developed to the point of making it an art form. However, it was not until much later in the human history that a scientific approach was taken to crystals; it probably occurred for the first time in 1669 when Steno observed quartz crystals and discovered that the angle between different faces was constant and independent of the size.1–3 In 1784 Haüy proposed the law of constant interfacial angles. So it is quite straightforward to assume that from the early days in crystallography, shape was the central issue.2,3 The first studies in this field were based on measuring the angles between faces and the symmetry relations on the crystals. Structure was obtained from the shape of the crystal since many polyhedral forms were observed such as cubes, octahedra, tetrahedra and others, therefore geometry became a major tool in describing crystals,4 a good example of this is the Euler relationship which allowed the calculation of the number of faces (F) on a polyhedron which is connected to the number of corners (C) and edges (E) by:| E = F + C − 2 | (1) |
Making the study of crystals an exact science even before the discovery of the atom, the French Physicist Auguste Bravais5 introduced the concept of lattice which implies that crystals are formed as a result of a periodic array of motifs. Translated into atomic view, motifs are atoms, and facets are now lattice planes, which correspond to the high-density planes of lattice atoms (Bravais Law).
Crystal structure can be explained in terms of imaginary planes where atoms would lie. These planes are the so-called lattice planes, which extend throughout the entire crystal structure intersecting the unit cells at specific points and which are generally described by Miller indices denoted as (h, k, l). The Miller indices, which describe lattice planes, tend to have small values, therefore shapes of crystals will be formed by facets with low-index Miller indices. Facets are also found in natural rocks. Fig. 1 shows some examples of minerals of calcite and sodium chlorate, proving that equilibrium in natural crystals sometimes implies faceting.
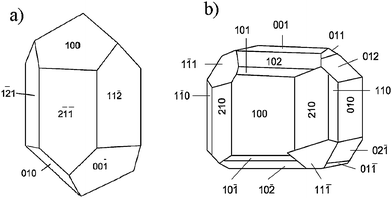 | ||
| Fig. 1 Schematic representation, showing the crystal faces of a) calcite (trigonal) and b) sodium chlorate (regular). | ||
Taking a more mathematical approach, a crystal lattice should have symmetry axis of order n. If a lattice vector T (joining two points) is rotated by an angle the vector −T is also a lattice vector. In general, a rotation will also produce the lattice vectors T′ or T′′ (Fig. 2) whose difference is also a lattice vector.
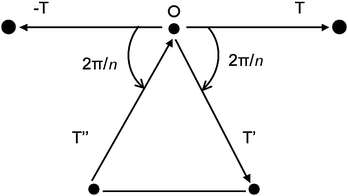 | ||
| Fig. 2 Lattice points in a plane normal to the symmetry axis n passing through O. | ||
From Fig. 2 we have that
| T′ − T′′ = mT |
2cos![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) [(2π/n) = m] [(2π/n) = m] | (2) |
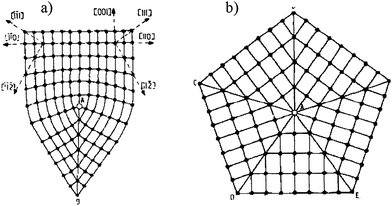
This equation is only valid for m = 1, 2, 3, 4, 6, where the space would be filled by rectangles, triangles, squares and hexagons.6 In other words, we can form a lattice (filling the space) with objects with symmetries other than 5. This leads into a very interesting fact; we cannot fill the space with a pentagon (Fig. 3a). No matter how we pack them we will leave gaps behind.7 If we now consider a regular tetrahedron and we try to produce a decahedron we have no choice other than leaving a gap (Fig. 3b), that somehow has to be closed to form decahedral particles.
![a) Regular pentagons cannot fill planar space. b) For perfect FCC tetrahedral subunits, the angle between adjacent {111} faces, illustrated here in the [110] projection, is 70.53°, which results in a 7.35° solid-angle deficiency. As a result of this deficiency, real nanoparticles must contain defects or be intrinsically strained.](/image/article/2010/NR/b9nr00287a/b9nr00287a-f3.gif) | ||
| Fig. 3 a) Regular pentagons cannot fill planar space. b) For perfect FCC tetrahedral subunits, the angle between adjacent {111} faces, illustrated here in the [110] projection, is 70.53°, which results in a 7.35° solid-angle deficiency. As a result of this deficiency, real nanoparticles must contain defects or be intrinsically strained. | ||
If we go back to the regular platonic solids, (Table 1), we should expect that crystals should have shapes such as cubes, tetrahedra or octahedra but no shapes such as the dodecahedron or the icosahedron which have five-fold symmetry axes. However, against what it is expected, these shapes are commonly observed in materials synthesized in the nano- and in the microscopic size range. Although macroscopic icosahedral shaped crystals are not naturally produced, five-fold nanoparticles have been found in meteorites8 and minerals.9–13 The reader is referred to the review of Hofmeister14 for further insight on this topic.
| Solid | Group |
|---|---|
| Cube | O h |
| Dodecahedron | I h |
| Icosahedron | I h |
| Octahedron | O h |
| Tetrahedron | T d |
Shapes of nanocrystals
As discussed in the previous section, five-fold symmetry is not allowed in bulk crystals, however, when we observe them in the nano- and mesoscopic ranges we can see that decahedral and icosahedral shapes can be produced in the whole size range as shown in Fig. 4, proving that five-fold structures can be produced from a few nm to thousands of nm. | ||
| Fig. 4 Electron microscopy images of an a) icosahedon of ∼80 nm, b) an icosahedron of about 7 nm, c) a decahedron of ∼300 nm, and d) a decahedron of few micrometres. | ||
In the case of the decahedra (as shown in Fig. 4b and c), when they are elongated, even very large nanowires15,16 (Fig. 5) can be produced with a five-fold symmetry axis. The question that comes in mind is, why are these produced?
 | ||
| Fig. 5 a) SEM image of a gold nanowire presenting a five-fold symmetry axis. b) Schematic representation of the nanowire. | ||
The “impossible” formation of particles with five-fold symmetry axes was a topic seriously debated in the sixties and seventies.17–25 One point of view assumed that a star disclination (Fig. 6) was responsible for closing the gap and it corresponded to inhomogeneous strain meanwhile; the other view, described the phenomenon by assuming a distortion that would lead to a rhombohedral lattice21,26 for the icosahedron and a body-centered orthorhombic lattice for the decahedron.17,21,27,28 This point was addressed more recently by Johnson et al.,29 who found that both kinds of mechanisms might be involved in the stabilization of materials presenting five-fold symmetry axes.
 | ||
| Fig. 6 Partial disclinations in FCC crystals. They are edge lines of twin boundaries that pass through the point A. a) The 70°32′ partial disclination. b) The 7°20′ (=360° − 5 × 70°32′) partial disclination (star disclination) that borders five twin boundaries. | ||
The main question that arises in order to understand the formation of these anomalous shaped nanocrystals is to consider if the Dh and Ih shapes are equilibrium shapes or are the result of the growth kinetics.30 An experiment to address this problem is shown in Fig. 7. A decahedral gold particle (Fig. 7a), which was synthesized by using a standard evaporation method, was heated inside an electron microscope by irradiation with the electron beam. The temperature was estimated to be a 500 °C during 3 min. By a simple analysis it can be demonstrated that the temperature produced by the beam can be expressed as T ∼ αr2 if a simple model of heat transfer is assumed. α was determined by calibration experiments at a fixed beam current. In this case the melting point of tin was obtained and then the value of α was taken to measure the temperature increase in the gold nanoparticle. Although this is an approximate method the values obtained are fairly accurate. The resulting structure (Fig. 7b) was still a decahedron but the facets are curved and grooves are developed resembling the Wulff polyhedron, which is expected to be an equilibrium structure.31,32 Similar results have been theoretically and experimentally obtained (Ag and Cu) confirming the growth kinetic effect as the main factor for the formation of such materials.33–37 For the case of C60 the data reported has also attributed the formation of icosahedral shapes to a kinetic origin.38–40
 | ||
| Fig. 7 HRTEM images of a) a synthesized decahedral particle. b) A heated decahedral particle. | ||
In a similar way, an icosahedral crystal was heated at the same temperature and the result was the dome-shaped crystal shown in Fig. 8. Therefore, we should infer that nanoparticles with a five-fold axis of symmetry are not equilibrium structures for sizes larger than 3 or 4 nm.41,42
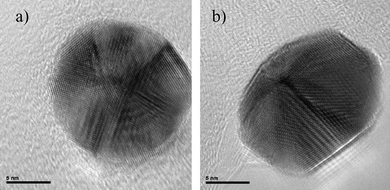 | ||
| Fig. 8 HRTEM images of a) an icosahedral nanoparticle and b) the same particle which has been heated inside a TEM. | ||
The relevant point to understand is how these structures are produced during the growth of the nanoparticle43 and how they are stabilized in order to form large nanoparticles which can reach several micrometres. In this work, we point out four main mechanisms that would stabilize the five-fold nanoparticles and that could lead into several-micrometre-sized decahedra or icosahedra.
Mechanism to stabilize fivefold nanoparticles
• Internal Strain.• Introduction of planar defects (twins, stacking faults).
• The introduction of steps, and kinks on the surface.
• External modification of shape by facet truncation.
• Other Mechanisms
In the following sections the different mechanisms will be discussed in detail.
Internal strain in nanoparticles
Nowadays, with the implementation of aberration-corrected transmission electron microscopy the internal strain produced in these structures44–47 can be studied in very high detail in both TEM and STEM, modes,48–50 opening up a whole new understanding at atomic level.51–56 An example of this work has been reported by Johnson et al.,29 who observed decahedral nanoparticles using Cs-corrected TEM. They found that, at least partially declinations relieve the strain. However, the complete mechanism appears to be more complex involving significant shear strain which suggests that a combination of the proposed models of Yacaman et al.18,19 and Marks20,57 must play a significant role in the stabilization of these materials. In the coming years it is expected that many results from aberration-corrected STEM/TEM will provide more extensive information on the strain mechanism. The main reason is that in STEM images particularly in the high-angle annular dark-field mode (HAADF-STEM) the intensity is ∼Z2 (Z = atomic number) and no dynamical effects contribute to the image. Therefore, variations in atomic distances observed on an image should be very close to the real value and therefore strain can be analyzed more accurately.Another technique, which has become very important in order to incorporate additional information, is weak-beam dark-field (WBDF) electron microscopy. In this method a dark-field image is obtained from a diffraction spot which is far from the Bragg condition. Very closely spaced thickness fringes are produced. By the use of WBDF electron microscopy48,49,58 it is possible to plot strains as shown in Fig. 9. This image was created using the (200) diffraction spot and tilted 2° away from the Bragg condition. An appealing image is produced where thickness lines produced by variations in thickness cross a region of high strain (see arrow). Therefore, it is possible to conclude that the shifting observed on the fringes is attributable to the strain on the nanoparticles. By measuring that shift, the strain can be estimated.
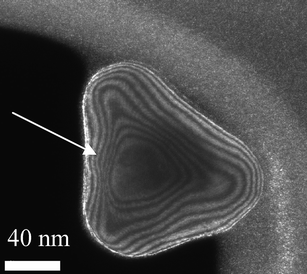 | ||
| Fig. 9 WBDF TEM image of a gold nanoparticle, where contour lines representing the thickness are observed. | ||
Planar defects in five-fold nanoparticles
The fact that particles as decahedra or icosahedra are composed of tetrahedral units linked by faces leads to the formation of defects, such as stacking faults or secondary twin boundaries, which releases stress by accommodating its contribution to the stabilization of the particles, as seen in Fig. 10. As mentioned above the WBDF electron microscopy technique has been proved to be a good method to observe defects on metal nanoparticles as faces linked by defects may appear with different contrasts (Fig. 10b and c).58 These defects are formed as a result of a minimization of the twin boundary energy,59 forming, in some cases, simple twin planes where two adjacent faces are perfect mirror planes, or in other cases, by the formation of more complex twin boundaries also involving additional stacking faults. Fig. 10c and d presents a decahedral gold nanoparticle recorded along the [110] orientation exhibiting five-fold symmetry, where the twin boundaries involve more than a single layer of atoms. | ||
| Fig. 10 a) TEM image of a star-shaped gold nanoparticle. b) WBDF TEM image of a) tilted 9°, where the defects in the crystal are highlighted by the different contrasts observed. c) TEM image of a rounded decahedral gold nanoparticle with very wide stacking faults. d) WBDF TEM image of c). | ||
Defects can also induce transformations of one structure into another. Koga et al.60 have shown that an Ih particle can transform into a Dh particle without diffusion when a cooperative slip dislocation of the (111) planes occurrs.
In order to explain defects on icosahedral nanoparticles, the structure can be considered as two pentagonal bipyramids joined with a common five-fold axis, to which ten additional tetrahedral units are added to complete the Ih structure. These tetrahedra become slightly distorted FCC tetrahedral units when each (111) face in the ten tetrahedra slips into the underlying (111) plane with a Burgers vector 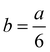 <112>. The collective deformation of the ten tetrahedra leaves a Dh structure, being a difussionless transformation. Another case has been described by Ascencio et al.61 who have reported the truncated icosahedral shape. This is produced by joining two decahedral structures and rotating them by 36° around the axis. This structure is formed by (111)-like facets with a triangular shape and (100)-like trapezoid facets. This structure was also found by Montejano et al.,62 who termed it “decmon” structure, and it is shown in Fig. 11. Rossi and Ferrando63 have also shown how polydecahedral nanoparticles can be produced including the Koga bydecahedral structure.64 So, it is possible to conclude that planar defects on nanoparticles may help to stabilize five-fold and more complex structures.
<112>. The collective deformation of the ten tetrahedra leaves a Dh structure, being a difussionless transformation. Another case has been described by Ascencio et al.61 who have reported the truncated icosahedral shape. This is produced by joining two decahedral structures and rotating them by 36° around the axis. This structure is formed by (111)-like facets with a triangular shape and (100)-like trapezoid facets. This structure was also found by Montejano et al.,62 who termed it “decmon” structure, and it is shown in Fig. 11. Rossi and Ferrando63 have also shown how polydecahedral nanoparticles can be produced including the Koga bydecahedral structure.64 So, it is possible to conclude that planar defects on nanoparticles may help to stabilize five-fold and more complex structures.
 | ||
| Fig. 11 Schematic representation of the ‘decmon’ decahedron. | ||
Steps and kinks
In order to introduce this topic we should discuss the standard model of a surface FK-L as terrace-kink-ledge, which was introduced in the 20s by Kossel65 and has been a cornerstone in understanding the formation of crystals. A schematic of this model is shown in Fig. 12 and it can be described as: a surface may contain flat terraces (A) step (or ledges) (B) and kinks (C).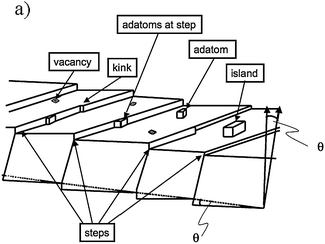 | ||
| Fig. 12 Schematic illustration of a vicinal surface with one-atom-layer high steps, kinks in steps, adatoms on terraces and at steps, vacancies and islands formed by a group of adatoms. | ||
Steps edges formed on crystals nanoparticles can play a crucial role in a variety of processes such as thermal roughening or faceting influencing the kinetics during crystal growth and as consequence the final morphology. These defects not only have a strong influence on the particle growth but also on the reactivity and much of the surface chemistry carried out of nanomaterials are believed to be related to their defects.66–73 The stepped faces formed on the solids commonly present high miller indices. In order to explain such extraordinary high values it is necessary to introduce long-range interactions between the atoms therefore, facets are stabilized when the range of interaction energy is increased to further neighboring pairs until corrugated faces appear (stepped or “vicinal” surfaces).74 High Miller indices facets commonly can be decomposed into lower indices. An example of the (199) vicinal surface will become → 4(100) × (111).75–77 This surface will make an angle of 8.43° with respect to <100>, as shown in Fig. 13.
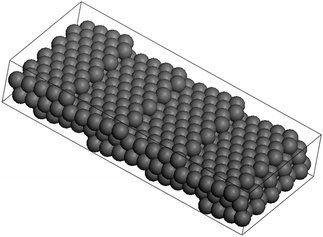 | ||
| Fig. 13 Ball model of the (119) surface of an FCC crystal. The surface consist of 4.5 atom wide terraces, separated by monatomic steps along the <110> direction. | ||
This rough surface can be smoothed by increasing the temperature. Corners and edges can become rounded as facets shrink finally disappearing over the “roughening transition temperature”,78TR, creating a smooth rounded surface when T > TR.
A good example of the stabilization of five-fold twined nanomaterials where high Miller indices are present in the structure has been described for Pt nanorods.79,80 In this material {hk0} high-index facets are formed in the central part which ends in decagonal pyramids exhibiting the five-fold symmetry.
In addition, surfaces will have adatoms, island vacancies and adatoms at a step to complete the structure.
If we want to calculate the surface free energy of a particle or crystal we should assume that for large enough particles (50 Å) steps, ledges, vacancies and kinks will be present. The surface free energy will be function of the temperature and of the density of steps ω. So we can write81
| Es(TP) = E0(T) + E1(T)ω + E3(T)ω3 | (3) |
We can ask now: Do the nanoparticles have steps and kinks? If we consider particles in the size range of >50 Å, the answer is yes. Ferrer et al.84 have demonstrated that in the case of Au/Pd, atomic-level HAADF-STEM images clearly revealed the steps and kinks on the surface. Fig. 14 shows the image and the calculated structure of an Au/Pd nanoparticle. This calculation was made by comparing the measured intensities with image calculations. The only way that a match can be found is by assuming a kinked and stepped surface on the particle.
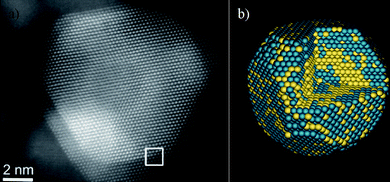 | ||
| Fig. 14 a) Aberration-corrected STEM image of an Au/Pd nanoparticle, the interface is marked by a white square. b) Calculated model for the Au/Pd nanoparticle. | ||
It is now clear that for particles >50 nm the steps become dominant. An example of a star-shaped particle can be seen in Fig. 15, where steps on the surface are clearly visible.
 | ||
| Fig. 15 High-resolution SEM image of a hexagonal-shaped gold nanoparticles presenting steps on the surface. b) High-resolution TEM image of a gold nanoparticle where linear defects are observed. | ||
Truncations, wedges and notches
A very general phenomenon observed in nanoparticles is the fact that truncations, wedges and notches are often observed in nanoparticles. Probably the most well known example is the Marks decahedron,85 which shows extra (111) facets in the form of notches. Recently, a truncation on the icosahedral structure86 has been proposed by Chui et al.87,88 These are only two cases of a more general trend. As particles grow larger there is a clear tendency to develop additional (111) facets. That results in the formation of higher polyhedral structures, shown in Fig. 16. The fact that part of the image is in focus where another portion is out of focus shows a height difference larger than the depth of focus of the TEM. The height was estimated by defocusing experiments in around 5–6 interatomic spacings. Of course, faceting will also be connected with kinks of the kind discussed in the previous section. At first glance it appears that truncations are just the result of growth kinetics. To illustrate this point we consider a square FCC crystal growing on a supersaturated solution. If the velocity of growth in the (100) direction is larger than the velocity along the (110) direction and fills the condition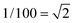 V110 then the crystal will retain a square shape (Fig. 17a). However, if for some reason V110 > V100 then a (110) truncation will be produced (Fig. 17b). Another example has been described by Elechiguerra et al.89 In this case twins in an initially hexagonal particle introduced facets with different growth speed and the particle became a triangular particle. Growth speed might be altered by surface phenomena such as impurity adsoprtion or surface reconstruction. However, it can be shown that truncation can also be the result of thermodynamical equilibrium. It appears that as the nanoparticle size increases, the truncation of facets will be more common. Fig. 17 shows truncated nanoparticles which are commonly observed during nanocrystal synthesis. Many of them are quite stable even after annealing.
V110 then the crystal will retain a square shape (Fig. 17a). However, if for some reason V110 > V100 then a (110) truncation will be produced (Fig. 17b). Another example has been described by Elechiguerra et al.89 In this case twins in an initially hexagonal particle introduced facets with different growth speed and the particle became a triangular particle. Growth speed might be altered by surface phenomena such as impurity adsoprtion or surface reconstruction. However, it can be shown that truncation can also be the result of thermodynamical equilibrium. It appears that as the nanoparticle size increases, the truncation of facets will be more common. Fig. 17 shows truncated nanoparticles which are commonly observed during nanocrystal synthesis. Many of them are quite stable even after annealing.
 | ||
| Fig. 16 High-resolution TEM image of different polyhedral metal nanoparticles. | ||
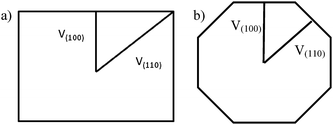 | ||
| Fig. 17 Schematic representation of a crystal growing at different velocities. | ||
Other mechanisms
Other relaxation mechanisms that involve the stabilization of nanoparticles with five-fold symmetry are related to the five-fold axis movement or splitting.46 The most important cases are:1 Displacement of the five-fold axis which reduces the elastic energy (Fig. 18a).
 | ||
| Fig. 18 Different ways of elastic energy relaxation in pentagonal particles. a) Shifting of the pentagonal axis and b) Decomposing the disclination into two others. | ||
2 Splitting of the five-fold axis (Fig. 18b). In this case a disclination can split in two or more partial disclinations having the same frank vector.90
Some other relaxation mechanisms might also be possible, but these will not be considered in the present paper.
Conclusions
In this review we have shown the importance of different aspects of the structure of nanoparticles which lead to the stabilization of five-fold and other shapes not seen on bulk crystals. This is part of the unique properties of such materials at the nanoscale level. It is logical to assume that most of these shapes are kinetically produced and therefore do not correspond to equilibrium shapes. However, five-fold structures remain stable for sizes up to 500 nm, and only by annealing the structure can an equilibrium shape be produced. In addition, vicinal surfaces are present in nanoparticles >50 nm, which would lead to very high Miller indices, that however, breakdown into low-index facets and ledges. The result is that particles will have a structure with kinks, vacancies and adsorbed atoms, which can contribute to improved catalytic properties. It is clear that the development of ultra-high-resolution TEM, STEM and SEM has contributed to advances in the understanding of nanoparticle structure.We have shown in this review that the structure of nanoparticles can be stabilized by several mechanisms such as strain, planar defects, kinks and steps among others. One of several of those mechanisms can operate in any given situation.
Acknowledgements
This work was performed with the support of NSF grant award DMR-0830074 “Alloys at the Nanoscale: The Case of Nanoparticles” and the Welch Foundation grant award AX-1615 “Controlling the Shape and Particles Using Wet Chemistry Methods and its Application to Synthesis of Hollow Bimetallic Nanostructures”. We are also indebted to Conacyt for supporting Alma Vazquez and Ruben Estrada. We are also indebted to Dave Olmos for his technical support and Mildred Herrera-Rosales for her help writing this work.References
- J. W. Gibbs, Trans. Connecticut Acad., 1878, 3, 343 Search PubMed.
- J. W. Gibbs, On the Equilibrium of Heterogeneous Substances, Longmans, Green & Co., New York, 1928 Search PubMed.
- G. Z. Wulff, Z. Kristallogr., 1901, 34, 449 CAS.
- H. P. Bonzel, Phys. Rep., 2003, 385, 1–67 CrossRef CAS.
- Aroyo and I. Mois, International Tables for Crystallography, Springer, Norwell, 2006 Search PubMed.
- A. Putnis, Introduction to Mineral Sciences, Cambridge University Press, Cambridge, 1992 Search PubMed.
- E. Kroner and K. H. Anthony, Annu. Rev. Mater. Sci., 1975, 5, 43 CrossRef.
- T. L. Daulton, D. D. Eisenhour, T. J. Bernatowicz, R. S. Lewis and P. R. Buseck, Geochim. Cosmochim. Acta, 1996, 60, 4853 CrossRef CAS.
- C. Hintze, Handbuch der Mineralogie. I Elemente und Sulfide, Verlag von Veit und Co., Leipzig, 1904 Search PubMed.
- F. Wallerant, Cristallographie, Librairie Polytechnique, Paris, 1909 Search PubMed.
- A. v. Fersmann and V. Goldschmidt, Der Diamant, Carl Winters Universitätsbuchhandlung, Heidelberg, 1911 Search PubMed.
- V. M. Goldschmidt, Atlas der Kristallformen, Carl Winters Universitätsbuchhandlung, Heidelberg, 1918 Search PubMed.
- C. Palache, H. Berman and C. Frondel, The System of Mineralogy of J.D. Dana and E.S. Dana; I. Elements, Sulfides, Sulfosalts, Oxides, John Wiley and Sons, New York, 1944 Search PubMed.
- H. Hofmeister, Encyclopedia of Nanoscience and Nanotechnology, Fivefold twinned nanoparticles, American Scientific Publ., North Lewis Way, 2003 Search PubMed.
- W. Zhang, P. Chen, Q. Gao, Y. Zhang and Y. Tang, Chem. Mater., 2008, 20, 1699 CrossRef CAS.
- B. Wiley, Y. Sun and Y. Xia, Acc. Chem. Res., 2007, 40, 1067 CrossRef CAS.
- B. G. Bagley, Nature, 1965, 208, 674.
- M. J. Yacamán, K. Heinemann, C. Y. Yang and H. Poppa, J. Cryst. Growth, 1979, 47, 187 CrossRef CAS.
- C. Y. Yang, M. J. Yacaman and K. Heinemann, J. Cryst. Growth, 1979, 47, 283 CrossRef CAS.
- L. D. Marks, Surf. Sci., 1985, 150, 302 CrossRef CAS.
- C. Y. Yang, J. Cryst. Growth, 1979, 47, 274–282 CrossRef CAS.
- J. G. Allpress and J. V. Sanders, Surf. Sci., 1967, 7, 1–25 CrossRef.
- S. Ino, J. Phys. Soc. Jpn., 1966, 21, 346–362 CAS.
- L. D. Marks and A. Howie, Nature, 1979, 282, 196–198 CAS.
- R. deWit, J. Phys. C: Solid State Phys., 1972, 5, 529–534 CrossRef CAS.
- A. Mackay, Acta Crystallogr., 1962, 15, 916 CrossRef CAS.
- J. A. R. Clarke and J. D. Bernal, Nature, 1966, 211, 280 CrossRef.
- B. G. Bagley, J. Cryst. Growth, 1970, 6, 323 CrossRef CAS.
- C. L. Johnson, E. Snoeck, M. Ezcurdia, B. Rodríguez-González, I. Pastoriza-Santos, L. M. Liz-Marzán and M. J. Hÿtch, Nat. Mater., 2008, 7, 120 CrossRef CAS.
- D. Schebarchov and S. C. Hendy, Eur. Phys. J. D, 2007, 43, 11–14 CrossRef CAS.
- H. P. Bonzel, Prog. Surf. Sci., 2001, 67, 45–48 CrossRef CAS.
- C. Herring, Phys. Rev., 1951, 82, 87 CrossRef CAS.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155408 CrossRef.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2000, 84, 5544–5547 CrossRef CAS.
- D. Reinhard, B. D. Hall, P. Berthoud, S. Valkealahti and R. Monot, Phys. Rev. Lett., 1997, 79, 1459–1462 CrossRef CAS.
- D. Reinhard, B. D. Hall, D. Ugarte and R. Monot, Phys. Rev. B: Condens. Matter, 1997, 55, 7868–7881 CrossRef CAS.
- B. D. Hall, M. Flüeli, R. Monot and J.-P. Borel, Phys. Rev. B: Condens. Matter, 1991, 43, 3906–3917 CrossRef.
- F. Baletto, J. P. K. Doye and R. Ferrando, Phys. Rev. Lett., 2002, 88, 075503 CrossRef CAS.
- W. Branz, N. Malinowski, H. Schaber and T. P. Martin, Chem. Phys. Lett., 2000, 328, 245–250 CrossRef CAS.
- T. P. Martin, U. Näher, H. Schaber and U. Zimmermann, Phys. Rev. Lett., 1993, 70, 3079–3082 CrossRef CAS.
- C. L. Cleveland, U. Landman, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Phys. Rev. Lett., 1997, 79, 1873–1876 CrossRef CAS.
- C. L. Cleveland, U. Landman, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Z. Phys. D, At., Mol. Clusters, 1997, 40, 503–508 CrossRef CAS.
- C. Lofton and W. Sigmund, Adv. Funct. Mater., 2005, 15, 1197 CrossRef CAS.
- A. E. Romanov, European Journal of Mechanics – A/Solids, 2003, 22, 727–741 Search PubMed.
- V. G. Gryaznov, M. Y. Gutkin, A. E. Romanov and L. I. Trusov, J. Mater. Sci., 1993, 28, 4359 CrossRef CAS.
- V. G. Gryaznov, A. M. Kaprelov, A. E. Romanov and I. A. Polonsky, Phys. Status Solidi B, 1991, 167, 441–450 CrossRef.
- J. P. Hirth and J. Lothe, Theory of Dislocations, McGraw Hill, New York, 1982 Search PubMed.
- M. José-Yacamán and M. Avalos-Borja, Catal. Rev. Sci. Eng., 1992, 34(1), 55.
- M. José-Yacamán, E. Pérez-Tijerina and S. Mejía-Rosales, J. Mater. Chem., 2007, 17, 1035 RSC.
- A. K. Datye and D. J. Smith, Catal. Rev. Sci. Eng., 1992, 34(1), 129 CAS.
- M. Haider, S. Uhlemann and J. Zach, Ultramicroscopy, 2000, 81, 163 CrossRef CAS.
- O. L. Krivanek, N. Delby and A. R. Lupini, Ultramicroscopy, 1999, 78, 1 CrossRef CAS.
- P. E. Batson, N. Dellby and O. L. Krivanek, Nature, 2002, 418, 617 CrossRef.
- D. A. Muller, Nat. Mater., 2009, 8, 263 CrossRef CAS.
- P. A. Midgley and M. Weyland, Ultramicroscopy, 2003, 96, 413 CrossRef CAS.
- V. Intaraprasonk, H. L. Xin and D. A. Muller, Ultramicroscopy, 2008, 108, 1454–1466 CrossRef CAS.
- L. D. Marks and D. J. Smith, J. Cryst. Growth, 1981, 54, 425 CrossRef CAS.
- A. Mayoral, A. Vazquez-Duran, H. Barron and M. Jose-Yacaman, Appl. Phys. A: Mater. Sci. Process., 2009, 97, 11–18 CrossRef CAS.
- T. Hahn and H. Klapper, International Tables for Crystallography, Kluwer, Dordrecht, 2003 Search PubMed.
- K. Koga, T. Ikeshoji and K. Sugawara, Phys. Rev. Lett., 2004, 92, 115507 CrossRef.
- J. A. Ascencio, P. M and M. José-Yacamán, Surf. Sci., 2000, 447, 73–80 CrossRef CAS.
- J. M. Montejano-Carrizales, J. L. Rodriguez-Lopez, C. Gutierrez-Wing, M. Miki-Yoshida and M. José-Yacamán, Encyclopedia of Nanoscience and Nanotechnology, 2004, 2, 237–282 Search PubMed.
- G. Rossi and R. Ferrando, Nanotechnology, 2007, 18, 225706 CrossRef.
- K. Koga, Phys. Rev. Lett., 2006, 96, 115501 CrossRef.
- W. Kossel, Nachr. Ges. Wissensch. Göttingen, 1927, 135 Search PubMed.
- E. D. Williams, Surf. Sci., 1994, 299–300, 502–524 CrossRef CAS.
- H. C. Jeong and E. D. Williams, Surf. Sci. Rep., 1999, 34, 171–294 CrossRef CAS.
- V. E. Henrich and P. A. Cox, The Surface Science of Metal Oxides, Cambridge Univ. Press, Cambridge, 1994 Search PubMed.
- H. J. Freund, Faraday Discuss., 1999, 114, 1–31 RSC.
- S. C. Petitto, E. M. Marsh and M. A. Langell, J. Phys. Chem. B, 2006, 110, 1309–1318 CrossRef CAS.
- B. D. Yu and M. Scheffler, Phys. Rev. B: Condens. Matter, 1997, 55, 13916–13924 CrossRef CAS.
- G. Kern and J.H. A, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2161–2169 CrossRef CAS.
- T. Jiang, D. J. Mowbray, S. Dobrin, H. Falsig, B. Hvolbæk, T. Bligaard and J. K. Nørskov, J. Phys. Chem. C, 2009, 113, 10548–10553 CrossRef CAS.
- R. C. Nelson, T. L. Einstein, S. V. Khare and P. J. Rous, Surf. Sci., 1993, 295, 462 CrossRef CAS.
- H. Ibach, Physics of Surfaces and Interfaces, Springer, Leipzig, 2006 Search PubMed.
- E. Lang, K. Muller, K. Heinz, M. A. VanHove, R. J. Koestner and G. A. Somorjai, Surf. Sci., 1983, 127, 347 CrossRef.
- D. L. Abernathy, S. G. J. Mochrie, D. M. Zehner, G. Grübel and D. Gibb, Phys. Rev. B: Condens. Matter, 1992, 45, 9272 CrossRef CAS.
- J. Lapujoulade, Surf. Sci. Rep., 1994, 20, 195 CrossRef.
- N. Tian, Z. Y. Zhou and S. G. Sun, J. Phys. Chem. C, 2008, 112, 19801–19817 CAS.
- Z. Y. Zhou, N. Tian, Z. Z. Huang, D. J. Chen and S. G. Sun, Faraday Discuss., 2009, 140, 81–92 RSC.
- A. S. Barnard and L. A. Curtiss, ChemPhysChem, 2006, 7, 1544 CrossRef CAS.
- G. Rao, D. B. Zhang and P. Wynblatt, Acta Metall. Mater., 1993, 3331 CrossRef CAS.
- W. Zhang, J. Cryst. Growth, 2006, 297, 169 CrossRef CAS.
- D. Ferrer, D. A. Blom, L. F. Allard, S. Mejía, E. Pérez-Tijerina and M. José-Yacamán, J. Mater. Chem., 2008, 18, 2442 RSC.
- L. D. Marks, Philos. Mag. A, 1984, 49, 81 CrossRef CAS.
- A. S. Barnard, G. Opletal, I. K. Snook and S. P. Russo, J. Phys. Chem. C, 2008, 112, 14848–14852 CrossRef CAS.
- Y. H. Chui, R. J. Rees, I. K. Snook, B. O'Malley and S. P. Russo, J. Chem. Phys., 2006, 125, 114703 CrossRef.
- Y. H. Chui, G. Grochola, I. K. Snook and S. P. Russo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 033404 CrossRef.
- J. L. Elechiguerra, J. Reyes-Gasga and M. Jose-Yacaman, J. Mater. Chem., 2006, 16, 3906–3919 RSC.
- A. E. Romanov and V. I. Vladimirov, Phys. Status Solidi A, 1983, 78, 11 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |
