Co-Doped ZnO nanoparticles: Minireview

Abstract

Diluted magnetic semiconductors with a Curie temperature exceeding 300 K are promising candidates for spintronic devices and spin-based electronic technologies. We review recent achievements in the field of one of them: Co-doped ZnO at the nanoparticulate scale.

---

Igor Djerdj

Igor Djerdj studied physics at the University of Zagreb, Croatia where he also received his Ph.D. degree in 2003. He completed his first postdoctoral study at the Max Planck Institute of Colloids and Interfaces in Potsdam, Germany. Afterwards he moved to the Swiss Federal Institute of Technology (ETHZ), Switzerland where he did his second postdoc. Since 2009 he has been a Scientific Associate at the Ruđer Bošković Institute, Croatia. His research interests include the structural characterization of a variety of materials with targeted applications, theoretical modelling of the electronic structure, liquid-phase synthesis of novel materials particularly inorganic–organic hybrids, diluted magnetic semiconductors, magnetic nanoparticles, and gas-sensing materials.

Zvonko Jagličić

Zvonko Jagličić obtained his Ph.D. in solid state physics in 1996 at the University of Ljubljana. He has a research position at the Institute of Mathematics, Physics and Mechanics and is an assistant professor at the Faculty of Civil and Geodetic Engineering in Ljubljana, Slovenia. His research interests include magnetic, electronic and structural properties of complex metallic alloys, nanoparticles and multiferroics.

Denis Arčon

Denis Arčon received his Ph.D. degree in physics at the University of Ljubljana, Slovenia, in 1998. He then took a postdoctoral position at the University of Sussex, UK. In 2000 he became a group leader at the Institute “Jožef Stefan” and an assistant professor at the Faculty of mathematics and physics of the University of Ljubljana where he is now a lecturer. His broad research interests include magnetic systems, superconductivity and inorganic nanostructures and he applies nuclear magnetic resonance, electron paramagnetic resonance and muon spin relaxation techniques to study these systems. In particular, he is focused on semiconducting nanostructures as well as on fulleride and pnictide superconductors.

Markus Niederberger

Markus Niederberger studied chemistry at the Swiss Federal Institute of Technology (ETH) Zürich, where he also received his Ph.D. degree in 2000. After a postdoctoral stay at the University of California, Santa Barbara, in 2002 he became group leader at the Max Planck Institute of Colloids and Interfaces at Potsdam. Since 2007 he has been Assistant Professor in the Department of Materials at ETH Zürich. His research interests include the liquid-phase synthesis of inorganic functional materials, investigation of formation and crystallization mechanisms, particle assembly and organic–inorganic hybrids. Targeted applications are in the field of lithium ion batteries, chemoresitive gas sensors, photocatalysis, and transparent conducting oxides.

---

Introduction

A simple search in Web of Science with just the single key word “ZnO” results in 34 058 hits (January 2010) within the various research areas including physics, chemistry, nanoscience, nanotechnology and interdisciplinary materials science. Such a large quantity of published research papers having ZnO as the study object reflects its importance as a multifunctional versatile II–VI semiconducting material with a direct wide bandgap (3.37 eV at RT), large excitonic binding energy (60 meV), and excellent optoelectronic and piezoelectric properties.¹ A new chapter concerning the ZnO-related research area has been opened upon doping it with transition metals like Fe, Co, Mn, Ni, Cr, or V, leading to materials with completely different behaviour towards magnetic and optical excitation. This new research direction is frequently entitled as diluted magnetic semiconductors (DMS) including, apart from ZnO, other semiconducting hosts. The intense interest is mainly driven by the search for new device applications in spin-based technologies. Having simultaneously semiconducting and magnetic properties, one can take the advantage of both the electron charge and the electron spin for information recording. On the way to the practical use of both charge and spin of electrons, two criteria must be fulfilled. Firstly, a relatively high concentration of magnetic elements should be introduced in the semiconducting matrix, and secondly a ferromagnetic ground state with a Curie temperatures (T_C) greatly exceeding room temperature should be obtained.^2,3 Both requirements are highly demanding in terms of synthesis implying that many reports are disclosed about attempts in achieving RT ferromagnetism.^4–33 As typical semiconducting hosts, metal oxides like ZnO, TiO₂, SnO₂, or In₂O₃ are usually considered. Unlike the diluted magnetic semiconductors based on III–V or II–VI group of elements showing ferromagnetism only at very low temperatures, these oxide-based DMSs exhibit ferromagnetism at higher temperatures and even above RT. They are also optically transparent making them suitable for magneto–optoelectronic applications, particularly for electrodes in solar cells. Among all these metal oxides, ZnO is relatively well understood from an experimental point of view, requiring an extensive systematic experimentation and data analysis. Well-defined doping and defect chemistry, the potential for transparent high-temperature applications, and the ability to lase or emit spontaneously at ultraviolet wavelengths make ZnO attractive for many device applications.³ Concerning applications in spintronics, n-type ZnO shows a relatively long room-temperature spin-coherence time.³⁴ Moreover, the possibility to generate both p- and n-type ZnO of low resistivity turns bipolar spintronics based on ZnO to a realistic option, and reports of both hole^18,35,36 and electron-mediated^37–39 ferromagnetism in ZnO DMSs are very controversial. Among the various oxide-based DMSs, ZnO doped with a small amount of cobalt has been the centre of interest. There are many studies reporting the preparation of Co-doped ZnO compounds using a wide variety of physical and chemical routes. The largest class of such compounds is prepared in the form of thin films, which is understandable from the applicative point of view. However, regardless of the form and in spite of the large number of papers published, the situation is far from being well understood and there is no unique agreement about the origin of the magnetic behaviour observed in most cases. Descending to nanoscale dimensions, additional effects related to the high surface-to-volume ratio appear, making the whole story about Co-doped ZnO DMS more complex, but also more interesting.

Here we briefly review recent achievements in the field of Co-doped ZnO from the magnetic ground state point of view during attempting RT ferromagnetism. We restrict ourselves to the subclass of nanoparticulate materials, highlighting the complex role of nanoscale dimension in determining the final magnetic properties. We focus on both numerous theoretical models for the elucidation of an intrinsic origin of the ferromagnetism, as well as on various experimental synthetic approaches in obtaining Co-doped ZnO nanoparticles. In this context, we will also settle our contribution to the field. Due to the large number of publications, it is not possible to provide an exhaustive overview of this topic. Instead, we have chosen just a representative number of instructive literature examples to elucidate some of the major aspects of Co-doped ZnO. In addition, we will present theoretical physical models, which describe and explain conditions in obtaining RT ferromagnetism.

Physical models

Various physical models exist for the general description of ferromagnetism in diluted magnetic semiconductors. Chronologically, the first proposed model of ferromagnetism driven by the exchange interactions between carriers and localized spins was the Zener model (s–d interaction).^40–42 It was originally developed for transition metals attempting to explain the origin of experimentally observed ferromagnetism. Zener postulated three simple principles which appear to govern the interaction between the incomplete d-shells of adjacent atoms. The first principle, which is valid for at least the fifth column (V, Nb, Ta) but also beyond, is that the spin correlation between the electrons in the incomplete d shell of a single atom is essentially the same independent of whether the atom is part of a solid or isolated in the gaseous state. The lowest energy state in the isolated atom is given by the electron configuration in which the incomplete d shell has the highest net electron spin (Hund's 1st rule), i.e., in which all unpaired electrons have spins pointing in the same direction. Accordingly, the incomplete d shell of an atom in a metal has also the highest net electron spin consistent with the number of electrons therein.⁴⁰

The second principle says that the exchange integral between d shells of adjacent atoms has always the same sign as in the H₂ molecule. The direct interaction between d shells of adjacent atoms leads to an antiferromagnetic configuration of the d shell spins.

Finally, the third principle means that the spin of an incomplete d shell is strongly coupled to the spin of the conduction electrons. This coupling tends to align the spins of the incomplete d shells in a ferromagnetic manner. As a consequence, three types of spin coupling govern the magnetic properties of the transition metals. The relative magnitudes of these three types of coupling in a particular metal determine the type of its magnetic behavior. Ferromagnetism will be observed in all systems for which the neighboring incomplete d shells are sufficiently far apart so that the indirect ferromagnetic coupling through the conduction electrons dominates over the direct antiferromagnetic coupling. Among the pure transition metals this condition is most likely to occur in the last elements of the first transition group.⁴⁰

Later on, in the theory of magnetic metals, the Zener model was abandoned, as neither the itinerant character of the magnetic electrons nor the quantum Friedel oscillations of the electron spin polarization around the localized spins were taken into account. Both features show to be critical parameters in the theory of magnetic metals. However, in the case of semiconductors, the effect of the Friedel oscillations averages to zero, because the mean distance between the carriers is greater than that between the spins. In such a case, the Zener model becomes equivalent to the second description of ferromagnetism developed by Ruderman, Kittel, Kasuya, and Yosida (RKKY model), which was shown to be responsible for the carrier-induced ferromagnetism in IV–VI compounds (Pb, Sn, Mn)Te. RKKY interaction, as originally proposed by Ruderman and Kittel, refers to a coupling mechanism of nuclear magnetic moments in explaining unusually broad nuclear spin resonance lines that had been observed in natural metallic silver.⁴³ The theory describes an indirect exchange coupling, where the nuclear spin of one atom interacts with a conduction electron via the hyperfine interaction. This conduction electron then interacts with another nuclear spin, thus creating correlation energy between the two nuclear spins. Alternatively, a scenario has been proposed based on the localization of inner d or f shell electron spins that couple to conduction spins in a metal via the exchange interaction. One prediction of the RKKY theory in a system consisting of thin magnetic layers separated by non-magnetic spacer material is ferromagnetic/antiferromagnetic oscillations as a function of the distance between the layers.

Let us focus now on the main subject of this Minireview, namely Co-doped ZnO nanoparticles. For the simplification of the problem, we will temporarily put the nanocrystalline nature of the Co-doped ZnO aside, and simplify the investigated system in such a way that it consists of randomly distributed magnetic impurities (Co atoms) within a ZnO matrix. Incorporation of the Co ions into the ZnO host either involves the replacement of ZnO atoms/ions on regular Zn sites, or positioning of Co on non-regular (i.e., interstitial) sites. But the magnetic properties of the final system depend on many more parameters including the concentration and distribution of the cobalt, type and concentration of defects, n-type doping, p-type doping, etc. Although they did not investigate exactly Co-doped ZnO, Dietl et al.⁴² have predicted possible realization of RT ferromagnetism in DMS based on ZnO and GaN as host materials. They used the Zener description of hole-mediated exchange interactions and theoretically predicted a Curie temperature above room temperature in p-type ZnO with 5% Mn atoms as dopants and a carrier concentration of 3.5 × 10²⁰ holes cm⁻³. But such an assumed p-type doping is in conflict with the n-type doping in native ZnO. Nevertheless, they claimed that even higher values of T_C are possible for materials with higher concentrations of holes and magnetic ions or consisting of lighter elements.

Using Monte Carlo simulations, Jalbout et al.⁴⁴ studied the RKKY indirect exchange interaction of doped magnetic Co ions in ZnO films. They showed that the RKKY interaction in Co-doped ZnO is long ranged and its magnitude is inversely proportional to the distance R from a central Co²⁺ ion. The sign oscillates with a frequency that depends on the concentration of the carrier. The long-distance sum of the RKKY indirect exchange energies is positive, indicating that these materials are ferromagnetic.

Sato and Katayama-Yoshida⁴⁵ have argued the possible stabilization of ferromagnetism by electron doping in Co-doped ZnO. Analyzing the density of states, they suggest that the ferromagnetism originates from the competition between the ferromagnetic double exchange interaction and the antiferromagnetic super exchange interaction. Based on ab initio calculations within the local density approximation using the Korringa–Kohn–Rostoker method combined with coherent potential approximation,⁴⁶ they found that the ferromagnetic state was stabilized by electron doping in the case of Fe-, Co- and Ni-doped ZnO.⁴⁷ As an illustrative example of their ab initio calculation, we show a comparison between ferromagnetic and spin-glass state of Co-doped ZnO, where the concentration of magnetic Co ions is in the range from 5 to 25% (step 5%). The system was examined under the conditions of electron (n-type ZnO) or hole doping (p-type ZnO) with the same concentration values as Co.

To create electron carriers, they introduced one more component of Ga at the Zn site, while the hole carriers were created by introducing N at the O site. Illustratively, the electron-doped Co-doped ZnO can be described as (Zn_1−x−yCo_xGa_y)O, while its hole-doped counterpart can be regarded as (Zn_1−xCo_x)(O_1−yN_y). Based on these configurations, the total energies were calculated for the spin-glass state and for ferromagnetic ordering, and their difference is plotted in Fig. 1 as a function of magnetic Co ion and carrier concentration. The key message which can be extracted from Fig. 1 is that the ferromagnetism in Co-doped ZnO might be attainable with electron doping. It is also deducible that higher concentration of magnetic Co ions as well as higher concentration of electron dopants lead to higher stabilization of ferromagnetism as a ground state. At this point it might be appropriate to mention several considerations of magnetic ground states for Co-doped ZnO from first principles. Lee and Chang considered different geometries of Co ion accommodations on Zn regular sites in a ZnO supercell.⁶ They investigated the magnetic interactions between the Co ions, particularly the interaction range and dependence on the crystal directions. The interesting finding is that the ferromagnetic state is more stable than the antiferromagnetic one when Co ions are continuously aligned along the c-axis, whereas the opposite is true for an alignment along the a₁ direction. The difference in the stability of magnetic states between these two alignments of Co atoms originates from the hexagonal symmetry of the wurtzite structure affecting thus the magnitude of the superexchange interaction. Another interesting result is related to the Co–Co distances and the range of magnetic interactions. By inspecting different supercell sizes (variation of Co–Co distances), they found that couplings between two Co ions are negligible for distances larger than 4.6 Å, suggesting that magnetic interactions are of rather short range. Finally, including electron doping the stability of the ferromagnetic state is drastically enhanced. Considering the electron doping effect related to the alignment of magnetic ions in the wurtzite cell, they found that in the case of continuously aligned Co ions the ferromagnetic state is greatly stabilized when electrons are doped above 0.5 electrons per Co atom. For Co pairs formed along the a₁-axis, the stabilization of the ferromagnetic state is significantly increased after doping with 1 electron per Co atom, while the stability of the antiferromagnetic state is almost unaffected for Co pairs along the c-axis direction.⁶ The most likely mechanism for stabilizing the ferromagnetic state is double exchange interactions induced by carriers as originally proposed by Zener. A similar finding was reported by Hu et al. who employed LDA + U calculation for the band structure of Co_0.25Zn_0.75O. They obtained a semiconducting band structure and predicted an antiferromagnetic order between nearest-neighbor magnetic ions via the middle O ion for a configuration free from intrinsic defects such as O vacancies and Zn interstitial.⁴⁸ Writing about first-principle considerations about Co-substituted ZnO, one should mention the contribution of Sluiter et al.⁴⁹ who developed a simple and general picture based on hybridization, superexchange, and double exchange that captures trends for the transition metal series in the short- and long ranged magnetic interactions in DMS. Long-range interactions necessary for ferromagnetism in DMSs can be mediated by defect induced states. According to their prediction both hole doping and electron doping promote ferromagnetism in Co-doped ZnO, which is in contrast with previously issued DFT predictions where only electron doping enhances ferromagnetism in Co-doped ZnO. Co has the best potential as a Zn substitutional dopant in ZnO for producing DMS when combined with a hole dopant such as Li_Zn or an electron dopant such as Cu_Zn or interstitial Zn.⁴⁹

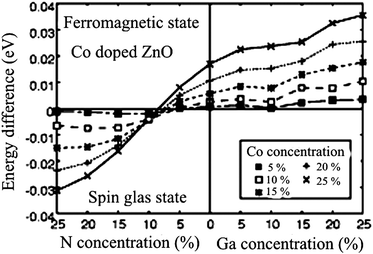Fig. 1 Stability of the ferromagnetic state in Co-doped ZnO as a function of carrier concentration. The vertical axis is the energy difference between the ferromagnetic and the spin-glass state. A positive energy difference indicates that the ferromagnetic state is more stable than the spin-glass state. The horizontal axis represents the concentration of additional dopants N and Ga which are used for creating charge carriers. Reproduced from ref. 47 with permission of the Japan Society of Applied Physics.

So far we reviewed several theoretical models and considerations describing the stability of the FM ground state in Co-doped ZnO. A recipe for obtaining ferromagnetism with T_C exceeding RT is to increase the number of itinerant d electrons, which is sufficient for the ferromagnetic coupling to prevail against the AFM superexchange interaction. The second requirement that enables ferromagnetic ordering is a large amount of Co ions incorporated in the ZnO matrix to reduce the Co–Co distances and thus to meet the short-range characteristics of FM interactions.

We finally come to the point where we take into account the nanoparticulate nature of Co-doped ZnO. The surface-to-volume ratio in nanoparticles is high in comparison to the corresponding bulk material, and therefore the surface effects are more pronounced with decreasing particle size. For the magnetic properties, the influence of uncompensated surface spins on the saturation magnetization plays a crucial role. Sanchez et al. investigated the local magnetic order at the polar (0001) oriented surface of ZnO.⁵⁰ Using first principles calculations, they showed that the surface enhances the spin polarization induced by Co atoms, and even in the absence of magnetic ions, it promotes the formation of p-derived extended magnetic states, which are missing in the bulk counterpart. In this way, the surface may show uncompensated spins ferromagnetically ordered, even for an antiferromagnetic alignment of Co impurities.

Finally, we proceed to the model suggested by Coey et al.,⁵¹i.e. spin-split impurity-band exchange or more often called shallow donor model. Double exchange mechanism, which has been proposed to explain ferromagnetism in Zn_1−xCo_xO, from the transition metals results in deep impurity band states.⁵² In contrast to that, the Coey model deals with shallow donor impurity bands. Without going too deep in Coey's assumptions, development and arguing, we will just mention the main features and consequences of the idea behind it. They discussed the ferromagnetic exchange coupling and magnetic moments in dilute n-type oxides in terms of tendencies of these materials to form shallow donors. Starting with the assumption that in magnetic cation substituted oxides, e.g., ZnO (Zn_1−xM_x), there are additionally donor defects (O□_δ, where δ denotes the defect concentrations). An electron associated with a particular defect will be confined in a hydrogenic orbital of radius r_H. For ZnO the value of r_H amounts to 0.76 nm. The binding energy of the electron donor in a 1s orbital (depth of the electron traps) is of the order of a few tenths of electron volts. As the donor concentration increases, the 1s orbitals overlap to form an impurity band. Firstly, the electrons remain localized due to the influence of correlations and potential fluctuations in a narrow band, until reaching the critical donor concentration at which the impurity band states become delocalized causing metallic conduction. The interaction between the magnetic cations and the hydrogenic electrons in the impurity band results in the formation of magnetic polarons, coupling the 3d moments of the ions within their orbits (magnetic polaron impurity-band model). The magnetic cations present an extra random potential, extending the localized region when their concentration increases. When the radius of the hydrogenic orbital is sufficiently large, an overlap between the hydrogenic electron and the cations within its orbit leads to ferromagnetic exchange coupling between them (s–d exchange).⁵³ In that paper,⁵¹ Coey et al. also estimated the Curie temperature and proposed conditions for obtaining ferromagnetism with high T_C (higher than room temperature). As a result of their calculation assuming that the modeled system is analogous to a Néel two-sublattice magnet (dopant cations and donor electrons), in the case of Co-doped ZnO (10% Co doping, 1% donor defects) T_C = 18 K. Of course, such a value is certainly too low particularly for any practical purposes and in contradiction with many experimental reports about Co-doped ZnO. Therefore, they suggested that the only way to boost T_C significantly is to increase the donor electron density in the vicinity of magnetic impurities. Matching the experimentally observed Curie temperatures would require 15% of the donor charge density to be redistributed over the impurity sites. In order to transfer around 1–2% of an electron from the donor states to each magnetic cation, empty 3d states have to hybridize with the donor states at the Fermi level. In conclusion to this model, the recipe for obtaining high Curie temperature requires hybridization and charge transfer from a shallow donor-derived impurity band to unoccupied 3d states at the Fermi level. It implies that the Coey model as well as Dietl's interpretation of the Zener model for hole-mediated ferromagnetism depend critically on three general factors: (a) concentration of the dopant x, (b) concentration of the carriers δ, and (c) strength of the interaction between them parameterized by 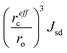. The cation radius scaling parameter 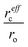accounts for enhanced hybridization of the magnetic dopant with the donor defects; J_sd represents the s–d exchange parameter. The sources of shallow donor in ZnO are defects which provide n-type conduction like oxygen vacancies and/or Zn interstitials.

At the end of this part of the review, we have to stress that we discussed different physical models that try to fit the observed ferromagnetism in DMS, particularly focusing on TM-doped ZnO, whereas TM is mainly Co. In particular, we mentioned the Zener model, the RKKY model, Dietl's application of the Zener model, the approach of Sato and Katayama-Yoshida, different first-principles calculations and finally the Coey model giving a prescription for achieving RT ferromagnetism in DMS. The main common feature of those contributions is the importance of an exchange interaction between the charge carriers introduced in the ZnO host through specific point defects and magnetic cations. In the following section of this Minireview, we will focus on the reported experimental achievements in the preparation of Co-doped ZnO at the nanoparticulate scale, reviewing the obtained final materials, the magnetic ground states. Additionally we try to put the obtained ferromagnetism in context with the described physical models.

Experimental findings

In the following part of the manuscript we mention important experimental achievements in the synthesis of Co-doped ZnO nanoparticles, including the determination of the magnetic ground state. For a better presentation to the readership, the main experimental findings are summarized in Table 1. Due to the limited available space, in the first column we just give the method of synthesis without including details about precursors, solvents, surfactants, reaction temperature, reaction duration, etc. In the second column, the obtained morphology is given, according to the information presented in the original manuscripts. The third column contains the information about the magnetic behavior of the system (RTFM: room-temperature ferromagnetism, FM: ferromagnetism). In the fourth column, additional important findings (if any), i.e., the interpretation of the obtained RTFM, are enclosed, or, if the system shows the deficiency of ferromagnetism, possible explanations offered by the authors are provided as well. Analyzing the experimental data, the first impression is that the majority of the authors were successful in obtaining room-temperature ferromagnetic Co-doped ZnO in nanoparticulate form. However, a closer look at these results raises several questions. The first issue is related to the increase of the ferromagnetism upon annealing at a higher temperature (823 K) for a short time (3 min).²⁹ An explanation offered for this phenomenon is related to the better crystallinity responsible for a higher saturation magnetization. During annealing, a relaxation process of the Co cations occurs, resulting in an improved homogeneous distribution of the dopants in the host materials, reaching an optimum coordination for magnetic interactions.²⁹ Such explanation can be put in the context of the mean field approximation based on RKKY interactions, where spin–spin coupling is assumed to be a long range interaction. One should also recall the DFT results of Lee and Chang who claimed that magnetic interactions are negligible when the Co–Co distance is larger than 4.6 Å.⁶ As a support of the strong dependence of ferromagnetism on the degree of structural order, ferromagnetism of Co-doped ZnO nanoparticles prepared by vaporization–condensation method revealed the strong dependence on the pressure in the solar reactor.¹⁹ Higher-pressure produces Co-enriched areas within the ZnO host, where the Co–Co distances are shorter, promoting thus antiferromagnetic coupling. The second effect of annealing is more profound on the high-temperature ferromagnetism in Co-doped ZnO and it is related to the type of the annealing atmosphere. It is well established that ZnO is native n-type material with the dopants generated from either O vacancies or Zn interstitials.⁵⁴ In the bound magnetic polaron (shallow donor impurity band) model, we met with the crucial role of shallow (electron) donors in the ferromagnetic coupling of Co cations. Kittilsveld et al. pointed out that the strong electronic coupling between magnetic cations and charge carriers at the Fermi level for the case of Co-doped ZnO can be described with the resonance equation: Co²⁺ + e⁻_donor ↔ Co⁺.³ The forward direction describes the formal transfer of the shallow donor's electron from Zn_i (zinc interstitial) to Co²⁺ to form Co⁺, while the reverse reaction describes a formal donor-type ionization process of the one electron reduced magnetic dopant. At equilibrium, this equation describes the dopant-donor hybridization crucial for achieving high T_C ferromagnetism in DMS, in accordance with the Coey model. Under a certain annealing atmosphere, some point defects will be generated, increasing the concentration of electron donors, while under some other types of atmosphere, point defect annihilation occurs, implying a decrease of magnetization and weakening of the FM state. It was experimentally observed that high-vacuum annealing results in the formation of a high number of oxygen vacancies in Co-doped ZnO nanowires promoting thus FM, while annealing in oxygen largely fills those vacancies up again with O, suppressing FM.⁵⁵ Another experimental finding elucidates the reversible ferromagnetic switching obtained by thermal treatment under N₂/O₂ atmosphere. Again, it was found that treatments under O₂ can switch off the FM, while treatment under N₂ can switch on ferromagnetism. Additional structural investigations of the materials before and after the annealing step were performed, evidencing the absence of any structural alteration upon heating. Therefore, the only conclusion is that the change in the concentration of point defects causes the change in the ferromagnetism.¹⁷ In the context of the influence of thermal treatments on the magnetic state of the final material, it would be interesting to consider any changes of the magnetic properties upon hydrogenation. Sol–gel prepared Co-doped ZnO was subjected to hydrogenation by exposing the sample to a plasma of Ar/H₂ mixed gas at room-temperature. Concerning the magnetic properties it was observed that hydrogenation causes an enhancement of the remnant and saturated magnetization.¹³ The possible interpretation of the observed phenomenon is related to the spin ordering at the molecular level interaction of the Co–H–Co complex. Such interpretation is rather unusual, since the authors don't consider the possible formation of point defects upon hydrogenation responsible for carrier-mediated magnetic exchange, but rather H incorporation as a stabilization factor in room-temperature ferromagnetism. Another interesting question is related to the influence of the nanoscale on the ferromagnetic features in Co:ZnO nanoparticles. There is experimental evidence about the saturation magnetization dependency on the crystallite size, i.e., it was found that M_s values decrease with increasing crystallite size and this is attributed to the trapping of free charge carriers in the grain boundaries leading to the variation of charge carriers occupying states. Such variation in turn influences the magnetic ordering in the samples, thereby decreasing the values of saturation magnetization.⁵⁶ In addition, the effect of system anisotropy (nanorods, nanowires) also enhances the magnetization values, and consequently stabilizes RTFM. This is due to the quantum confinement effect which induces the magnetization in ZnO nanowires. There is a recent report about an enhancement of hole-mediated magnetization due to the size effect.⁵⁷ Based on first principle calculations, Peng et al. showed that the size effect (anisotropic morphology with small diameter) could reduce the critical hole concentration for stabilizing the magnetization. Moreover, the critical holes concentration in the case of acceptor doping needed to induce ferromagnetism is less than 1/8 of that needed in bulk materials. This implies that in such low-dimensional anisotropic structures Zn vacancies play an important role and more Co dopants are bound inside magnetic polarons, thus increasing the probability for FM coupling between two magnetic ions within the same orbital.⁸

Table 1 Overview of the reported experimental results considering the examination of the magnetic ground state of Co-doped ZnO nanoparticles

Preparation method	Obtained morphology	Magnetic state	Important remark
Polymerizable precursor method	Agglomerated irregular nanoparticles (20–100 nm)	RTFM	Specific magnetization varies with particle size and lattice parameter c.^58
Hydrothermal method	Spherical nanoparticles (50–100 nm) + nanorods (D = 100–200 nm, L = 200–500 nm)	RTFM	Interfacial defects of particle interfaces acts as large volume magnetic polarons which couple the spins.^59
Hydrothermal method	Nanorods (D = 200 nm, L = 1–6 μm)	Weak RTFM	Ref. 60
Modified microemulsion route	Single-crystalline nanorods (D = 80–100 nm, L = 1.5–2 μm)	RTFM (TC > 380 K)	Ref. 10
Surfactant-assisted hydrothermal technique	Nanorods (D = 200–500 nm, L = several μm)	Weak RTFM + paramagnetic contribution	The origin of the ferromagnetism is probably due to the presence of mixed cation valence via d–d double-exchange mechanism.^1
Thermal hydrolysis	10 nm nanoparticles	RTFM	Oxygen vacancies as a donor impurity within the Coey model.^61
Sol–gel	Nanocomposite	Paramagnetic behavior	The paramagnetism is interpreted as a result of the low effective doping and the lack of oxygen vacancies.^62
Sol–gel	20 nm spherical nanocrystals	RTFM	RTFM induced by hydrogenation.^13
Sol–gel	Not reported	RTFM	Annealing of the material at higher temperatures yields larger ferromagnetism.^29
Sol–gel	140 nm nanoparticles	Paramagnetic behavior and low-temperature (150 K) FM	The magnetic observations are explained by mean-field Zener model.^16
Modified sol–gel	Nanorods (D = 100–200 nm, L = 200–1000 nm)	RTFM	Ref. 7
Solvothermal synthesis	Faceted core-shell 50 nm nanocrystals	RTFM	Ferromagnetic core + paramagnetic shell; RTFM is interpreted in the frame of bound magnetic polaron model based on the presence of doubly occupied oxygen vacancies or zinc interstitial.^21
Solvothermal synthesis	Nanoparticles, nanorods, nanowires	RTFM or AFM	The obtained morphology as well as magnetic coupling strongly depends on the solvent used.^63,64
Solvothermal synthesis under 12 T magnetic field	Single-crystalline nanorods (L = 50–200 nm)	0 T-paramagnetic behavior 12 T- RTFM	External magnetic field influences the growth and the final magnetic behavior.^12
Autocombustion method	Nanoparticles (15 or 40 nm)	Paramagnetic or RTFM	RTFM attributed to the presence of metallic Co impurities.^27
Autocombustion method	40 nm nanoparticles	FM imbedded in paramagnetic matrix^25or paramagnetic behavior^22	Ref. 22,25
Vaporization–condensation method	Tetrapod-like morphology	Ferromagnetic (p = 10 Torr), paramagnetic (p = 70–100 Torr)	Magnetic properties can be tuned by the proper control of the preparation conditions. The defective microstructure favors the formation of Co enriched areas inside ZnO matrix, therefore decreasing Co–Co distances and promoting AF interactions.^19
Hydrothermal + electrochemical process	Hexagonal ring-like superstructure composed of nanorods (100–400 nm in thickness)	RTFM	The experimental evidence of oxygen vacancies which stabilize the FM state.^11
Alkaline-activated hydrolysis and condensation	20 nm spherical nanoparticles	Paramagnetic behavior	Spinodal decomposition cannot be solely responsible for the appearance of FM.^26
Thermal decomposition	Nanowires (D = 45 nm, L = 2–6 μm)	RTFM	The FM ordering is induced by the Zn vacancy-derived impurity band and enhanced by the 1D size effect.^8
Thermal decomposition	6 nm nanocrystals	RTFM	Ref. 33
Thermal decomposition	Nanowires (D = 35 nm, L = 2–6 μm)	Weak FM behavior	Ref. 65
Acrylamide polymerization method	40 nm nanoparticles	RTFM + paramagnetic component	The annealing under N2/O2 atmosphere can switch on/off ferromagnetism in Co-doped ZnO.^17

---

Co-Doped ZnO nanorods by benzyl alcohol reaction pathway

In the preceding two sections we gave a brief overview of both theoretical and experimental achievements in the field of one representative system of diluted magnetic semiconductors: Co-doped ZnO nanoparticles. In the following part we will shortly report on our own contribution to the field of DMS presenting the magnetic properties of Co-doped ZnO nanorods.

ZnO nanorods were synthesized using a simple and straightforward non-aqueous sol–gel method, based on benzyl alcohol as a solvent. Details about the synthesis and structural characterization were published elsewhere.³²

TEM images of 3% Co:ZnO nanorods displayed in Fig. 2(a) and 2(b) point to a nanorod-like morphology with the sizes measured along and perpendicular to their axes. The average length is 129 nm and average diameter 44 nm for 3% Co:ZnO, while 5% Co:ZnO exhibiting rather irregular shape with the appearance of polyhedral crystallites measures around 170 nm in length. The HRTEM image (Fig. 2(c)) shows a good crystallinity with clear resolution of lattice fringes.

Fig. 2 (a) TEM image of 3% Co:ZnO nanorods; (b) higher magnification; (c) HRTEM image of 3% Co:ZnO nanorod.

In Fig. 3(a) the temperature dependence of the magnetic susceptibility χ(T) measured after a zero-field cooling (ZFC) and field cooling (FC) procedures are shown. Over most of the studied temperature interval, it shows only weak temperature dependence. The susceptibility χ(T) is systematically larger under FC conditions when compared to the values obtained after the ZFC procedure. The enhanced difference between ZFC and FC susceptibilities below ≈140 K may reflect the blocking temperature T_B of the assembly of superparamagnetic particles. A relatively “flat” ZFC curve without a pronounced maximum indicates a broad distribution. To prove the magnetic ground state, we measured an isothermal magnetization at 2 K and at room temperature. In Fig. 3(b) the magnetization curves M(H) are displayed for undoped ZnO nanorods and both Co-doped samples. The Co-doped samples show “S”-shaped curves typical for a ferromagnet with magnetizations that saturate almost completely at 50 kOe at M_sat = 3.5 emu g⁻¹ and 6.3 emu g⁻¹ for 3% and 5% doped samples, both values at T = 2 K. If all Co²⁺ (S = 3/2 in the high-spin configuration) moments were ferromagnetically ordered, the expected saturation magnetizations would be 6.2 emu g⁻¹ and 10.3 emu g⁻¹. The lower experimental values point to the fact that the final doping levels in Co-doped ZnO are below the nominal values of 3% and 5%.

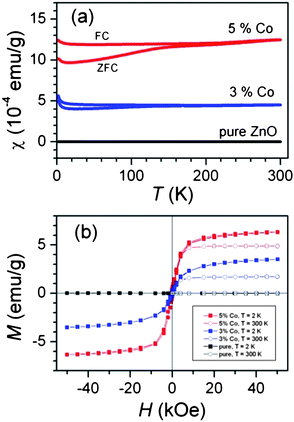Fig. 3 (a) The temperature dependence of the susceptibility and; (b) hysteresis loops measured at T = 2 K and 300 K. For comparison the small signal of undoped (pure) ZnO is shown, too. Reproduced from ref. 32 with permission of the Royal Society of Chemistry.

The room temperature saturation magnetizations are lower than the corresponding values at 2 K. The result suggests that the samples, in addition to the ferromagnetic contribution with temperature independent magnetization as described above, also exhibit a paramagnetic part with Curie-like susceptibility dependence (notice the Curie upturns at low temperatures in Fig. 3(a)). The coercive field is also detected and is around 0.3 kOe for both dopant levels at 2 K. The M(H) curves were fitted with the Langevin function, where the average magnetic moment per particle was obtained μ ≈ 12 μ_B and 18 μ_B for 3% and 5% doped samples. If the Co²⁺ ions are distributed homogeneously, then the average particle size would be around 26 nm. We notice here that our particle size estimation coincides very well with the reported value, and thus allows a good comparison.¹⁹

The EPR signal was measured at several temperatures up to 635 K, which is well above room temperature. A very broad signal with an irregular line shape is observed. The obtained spectra reproduce neither the paramagnetic resonances,⁶⁶ nor the resonance measured in ferromagnetic Co-doped ZnO.⁶⁷ It is very probable that the broad EPR signal is a ferromagnetic resonance. The open question is related to the physical model which is best suited to our observed RTFM in Co-doped ZnO prepared by the benzyl alcohol route. Within the frame of the bound magnetic polaron model and the Kittilstved study of the electronic structural origin of polarity dependent RTFM, we may suggest that the coupling between Co cations and shallow donor electrons at the Fermi level is responsible for the observed RTFM. However, the origin of point defects is still unclear and would require a further study. For sure, we can state that the oxygen vacancies are precluded in our system based on EPR results, making zinc interstitials possible candidates for a shallow donor source.

Conclusions

The foregoing overview underlines the importance of the magnetic properties research in the field of doped nanostructures. Although in our review we just focused on the single semiconducting system ZnO, and only one type of dopant Co, a diversity of existing physical models and experimental findings prove the complexity of such doped nanostructured systems. Of course, a broad list of potential applications of DMSs represent a high motivation for researchers to develop these and related materials. We mentioned several relevant theoretical (physical) models which try to fill the gap in the understanding of high-T_C ferromagnetism of Co-doped ZnO and more general in magnetic semiconductors. We also reviewed experimental findings highlighting the factors and features which characterize the appearance of RTFM in Co doped ZnO restricting to the nanoparticulate system. Finally, we added our contribution to the field, i.e., we have shown that our magnetization and EPR measurements strongly support a ferromagnetic behavior of the doped samples prepared by the benzyl alcohol route with T_C exceeding room temperature.

Acknowledgements

This work has been supported by the Croatian Ministry of Science, Education and Sport, grant No. 098-0982886-2894, and by the National Foundation of Science and High Education and Technological Development of the Republic of Croatia.

References

1. X. Wang, R. K. Zheng, Z. Liu, H. P. Ho, J. B. Xu and S. P. Ringer, Nanotechnology, 2008, 19, 455702.
2. H. Ohno, Science, 1998, 281, 951–956.
3. K. R. Kittilstved, W. K. Liu and D. R. Gamelin, Nat. Mater., 2006, 5, 291–297.
4. L. B. Duan, G. H. Rao, Y. C. Wang, J. Yu and T. Wang, J. Appl. Phys., 2008, 104, 013909.
5. J. B. Cui, Q. Zeng and U. J. Gibson, J. Appl. Phys., 2006, 99, 08M113.
6. E. C. Lee and K. J. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 085205.
7. S. Maensiri, P. Laokul, J. Klinkaewnarong and C. Thomas, Appl. Phys. A: Mater. Sci. Process., 2009, 94, 601–606.
8. T. Yao, W. Yan, Z. Sun, Z. Pan, Y. N. Xie, Y. Jiang, J. Ye, F. Hu and S. Q. Wei, J. Phys. Chem. C, 2009, 113, 14114–14118.
9. C. Song, K. W. Geng, F. Zeng, X. B. Wang, Y. X. Shen, F. Pan, Y. N. Xie, T. Liu, H. T. Zhou and Z. Fan, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 024405.
10. P. Che, W. B. Liu, L. Guo, L. He and C. P. Chen, J. Magn. Magn. Mater., 2008, 320, 2563–2566.
11. Y. J. Li, C. Y. Wang, M. Y. Lu, K. M. Li and L. J. Chen, Cryst. Growth Des., 2008, 8, 2598–2602.
12. D. W. Chu, Y. P. Zeng and D. L. Jiang, J. Phys. Chem. C, 2007, 111, 5893–5897.
13. S. H. Lee, Y. C. Cho, S. J. Kim, C. R. Cho, S. Y. Jeong, S. J. Kim, J. P. Kim, Y. N. Choi and J. M. Sur, Appl. Phys. Lett., 2009, 94, 212507.
14. J. L. MacManus-Driscoll, N. Khare, Y. L. Liu and M. E. Vickers, Adv. Mater., 2007, 19, 2925–2929.
15. W. B. Jian, I. J. Chen, T. C. Liao, Y. C. Ou, C. H. Nien, Z. Y. Wu, F. R. Chen, J. J. Kai and J. J. Lin, J. Nanosci. Nanotechnol., 2008, 8, 202–211.
16. J. H. Yang, L. Y. Zhao, X. Ding, L. L. Yang, Y. J. Zhang, Y. X. Wang and H. L. Liu, Mater. Sci. Eng., B, 2009, 162, 143–146.
17. D. Rubi, J. Fontcuberta, A. Calleja, L. Aragones, X. G. Capdevila and M. Segarra, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155322.
18. K. R. Kittilstved, N. S. Norberg and D. R. Gamelin, Phys. Rev. Lett., 2005, 94, 147209.
19. B. Martínez, F. Sandiumenge, L. Balcells, J. Arbiol, F. Sibieude and C. Monty, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165202.
20. K. R. Kittilstved, J. L. Zhao, W. K. Liu, J. D. Bryan, D. A. Schwartz and D. R. Gamelin, Appl. Phys. Lett., 2006, 89, 062510.
21. X. F. Wang, J. B. Xu, N. Ke, J. G. Yu, J. Wang, Q. Li, H. C. Ong and R. Zhang, Appl. Phys. Lett., 2006, 88, 223108.
22. L. B. Duan, W. G. Chu, J. Yu, Y. C. Wang, L. N. Zhang, G. Y. Liu, J. K. Liang and G. H. Rao, J. Magn. Magn. Mater., 2008, 320, 1573–1581.
23. K. R. Kittilstved and D. R. Gamelin, J. Appl. Phys., 2006, 99, 08M112.
24. H. Ohno, J. Magn. Magn. Mater., 2004, 272–276, 1–6.
25. L. B. Duan, G. H. Rao, J. Yu and Y. C. Wang, Solid State Commun., 2008, 145, 525–528.
26. M. A. White, O.S.T. and D. R. Gamelin, Chem. Mater., 2008, 20, 7107–7116.
27. S. Deka, R. Pasricha and P. A. Joy, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 033201.
28. T. Tamura and H. Ozaki, J. Phys.: Condens. Matter, 2009, 21, 026009.
29. X. Y. Zhou, S. H. Ge, D. S. Yao, Y. L. Zuo and Y. H. Xiao, Phys. B, 2008, 403, 3336–3339.
30. I. J. Chen, Y. C. Ou, Z. Y. Wu, F. R. Chen, J. J. Kai, J. J. Lin and W. B. Jian, J. Phys. Chem. C, 2008, 112, 9168–9171.
31. Y. Belghazi, G. Schmerber, S. Colis, J. L. Rehspringer and A. Dinia, Appl. Phys. Lett., 2006, 89, 122504.
32. I. Djerdj, G. Garnweitner, D. Arcon, M. Pregelj, Z. Jaglicic and M. Niederberger, J. Mater. Chem., 2008, 18, 5208–5217.
33. S. D. Kshirsagar, D. Inamdar, I. K. Gopalakrishnan, S. K. Kulshreshtha and S. Mahamunia, Solid State Commun., 2007, 143, 457–460.
34. S. Ghosh, V. Sih, W. H. Lau, D. D. Awschalom, S. Y. Bae, S. Wang, S. Vaidya and G. Chapline, Appl. Phys. Lett., 2005, 86, 232507.
35. S. W. Lim, M. C. Jeong, M. H. Ham and J. M. Myoung, Jpn. J. Appl. Phys., 2004, 43, L280–L283.
36. N. S. Norberg, K. R. Kittilstved, J. E. Amonette, R. K. Kukkadapu, D. A. Schwartz and D. R. Gamelin, J. Am. Chem. Soc., 2004, 126, 9387–9398.
37. H. Saeki, H. Tabata and T. Kawai, Solid State Commun., 2001, 120, 439–443.
38. D. A. Schwartz and D. R. Gamelin, Adv. Mater., 2004, 16, 2115–2119.
39. M. Venkatesan, C. B. Fitzgerald, J. G. Lunney and J. M. D. Coey, Phys. Rev. Lett., 2004, 93, 177206.
40. C. Zener, Phys. Rev., 1951, 81, 440–444.
41. C. Zener, Phys. Rev., 1951, 83, 299–301.
42. T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Science, 2000, 287, 1019–1022.
43. M. A. Ruderman and C. Kittel, Phys. Rev., 1954, 96, 99–102.
44. A. F. Jalbout, H. Chen and S. L. Whittenburg, Appl. Phys. Lett., 2002, 81, 2217–2219.
45. K. Sato and H. Katayama-Yoshida, Jpn. J. Appl. Phys., 2000, 39, L555–L558.
46. H. Akai, Phys. Rev. Lett., 1998, 81, 3002–3005.
47. K. Sato and H. Katayama-Yoshida, Jpn. J. Appl. Phys., 2001, 40, L334–L336.
48. S. J. Hu, S. S. Yan, M. W. Zhao and L. M. Mei, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245205.
49. M. H. F. Sluiter, Y. Kawazoe, P. Sharma, A. Inoue, A. R. Raju, C. Rout and U. V. Waghmare, Phys. Rev. Lett., 2005, 94, 187204.
50. N. Sanchez, S. Gallego and M. C. Munoz, Phys. Rev. Lett., 2008, 101, 067206.
51. J. M. Coey, M. Venkatesan and C. B. Fitzgerald, Nat. Mater., 2005, 4, 173–179.
52. M. H. F. Sluiter, Y. Kawazoe, P. Sharma, A. Inoue, A. R. Raju, C. Rout and U. V. Waghmare, Phys. Rev. Lett., 2005, 94, 187204.
53. A. C. Durst, R. N. Bhatt and P. A. Wolff, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235205.
54. D. C. Look, J. W. Hemsky and J. R. Sizelove, Phys. Rev. Lett., 1999, 82, 2552–2555.
55. Z. Y. Wu, F. R. Chen, J. J. Kai, W. B. Jian and J. J. Lin, Nanotechnology, 2006, 17, 5511–5518.
56. Y. K. Lakshmi, K. Srinivas, B. Sreedhar, M. M. Raja, M. Vithal and P. V. Reddy, Mater. Chem. Phys., 2009, 113, 749–755.
57. H. W. Peng, H. J. Xiang, S. H. Wei, S. S. Li, J. B. Xia and J. B. Li, Phys. Rev. Lett., 2009, 102, 017201.
58. S. Maensiri, J. Sreesongmuang, C. Thomas and J. Klinkaewnarong, J. Magn. Magn. Mater., 2006, 301, 422–432.
59. S. Maensiri, P. Laokul and S. Phokha, J. Magn. Magn. Mater., 2006, 305, 381–387.
60. C. Y. Lin, W. H. Wang, C. S. Lee, K. W. Sun and Y. W. Suen, Appl. Phys. Lett., 2009, 94, 151909.
61. Y. F. Liao, T. W. Huang, M. Z. Lin, K. L. Yu, H. S. Hsu, T. H. Lee, C. H. Lee and J. C. A. Huang, J. Magn. Magn. Mater., 2007, 310, E818–E820.
62. T. F. Shi, S. Y. Zhu, Z. H. Sun, S. Q. Wei and W. H. Liu, Appl. Phys. Lett., 2007, 90, 102108.
63. G. Clavel, M. G. Willinger, D. Zitoun and N. Pinna, Adv. Funct. Mater., 2007, 17, 3159–3169.
64. G. Clavel, N. Pinna and D. Zitoun, Phys. Status Solidi A, 2007, 204, 118–124.
65. B. D. Yuhas, S. Fakra, M. A. Marcus and P. D. Yang, Nano Lett., 2007, 7, 905–909.
66. A. O. Ankiewicz, M. C. Carmo, N. A. Sobolev, W. Gehlhoff, E. M. Kaidashev, A. Rahm, M. Lorenz and M. Grundmann, J. Appl. Phys., 2007, 101, 024324.
67. P. Sati, R. Hayn, R. Kuzian, S. Regnier, S. Schafer, A. Stepanov, C. Morhain, C. Deparis, M. Laugt, M. Goiran and Z. Golacki, Phys. Rev. Lett., 2006, 96, 017203.

---