Morphological and phase stability of zinc blende, amorphous and mixed core–shell ZnS nanoparticles†
A. S.
Barnard
a,
C. A.
Feigl
ab and
S. P.
Russo
*b
aCSIRO Materials Science and Engineering, Private Bag 33, Clayton South, VIC 3169, Australia. Fax: +61 3 9545 2059; Tel: +61 3 9545 7840
bApplied Physics, School of Applied Sciences, RMIT University, GPO Box 2476, Melbourne, Victoria 3001, Australia. E-mail: salvy.russo@rmit.edu.au
First published on 2nd September 2010
Abstract
Zinc sulfide (ZnS) nanoparticles are of interest for their luminescent and catalytic properties which are being considered for the next generation of optical, electronic and photovoltaic devices. However, ZnS nanoparticles undergo reversible and irreversible phase transformations under ambient conditions, so a detailed understanding of the nanomorphology is critical in ensuring these desirable properties can be controlled and maintained. Anticipating the structure and transformations in ZnS nanoparticles experimentally is difficult, since selectivity among competing phases, shapes and sizes is intrinsically linked. Presented here are the results of first principle computer simulations and advanced theoretical modelling used to investigate the relationship between size and shape in determining the crystallinity of ZnS nanoparticles. We find that the equilibrium morphology is characterised by {220} facets, irrespective of the size of the particle, but that the presence of different high energy facets introduced kinetically may significantly influence the zinc blende to amorphous ZnS transformation size, as well as the agglomeration behaviour. In addition to this, we model the relationship between transformation size, morphology and the ratio of crystalline core to amorphous shell and show that at small sizes, a core–shell crystalline/amorphous structure is thermodynamically favourable.
Introduction
Metal sulfides are an important class of materials which are currently being exploited in a variety of important applications. Among them, zinc sulfide (ZnS), a class II–VI direct band gap semiconductor, exhibits a range of desirable physical and chemical properties, which have been extensively studied and applied in various fields.1–3In general, ZnS nanostructures can be synthesized in a variety of morphologies including zero-dimensional nanoparticles, one-dimensional nanowires, nanorods, nanoribbons and nanobelts, as well as 2-D nanosheets4 and more complicated tetrapods and nanoflowers, depending on the growth precursors, temperature and the presence of catalysts.1,4 In particular, ZnS nanoparticles are the focus of many promising applications including field effect transistors for sensitive detection of biological species,5 ultraviolet-light sensors with high spectral sensitivity and high photosensitivity,6 temperature sensors,7 hydrogen sensors,8 field emitters,9 and heterojunction solar cells with high photovoltaic efficiency.10 Nanoparticles of ZnS are often doped with impurities such as manganese or copper to improve their luminescent properties, and are often used to ‘cap’ or form a shell around a core nanoparticle consisting of a similar II–VI semiconductor, such as CdS or CdSe.11,12 A large variety of synthesis techniques are available for producing ZnS nanoparticles, as described in ref. 3.
However, the preferred solid phase of this material is sensitive to changes in the thermal and chemical environment, even under ambient conditions.13 ZnS nanoparticles are inherently unstable and have the potential to undergo uncontrolled reversible and irreversible post-fabrication, solid–solid phase transformations, which can alter or completely eliminate desirable material properties. This throws into question the long term reliability of devices based on the phase dependent properties of this material. If robust ZnS-based nanotechnologies are to become a reality, a detailed knowledge of preferred shapes, phase stabilities and transformations is critical. For these reasons the structure and phase transformations of ZnS nanoparticles have received considerable attention.13–21 A detailed review of this phenomenon is provided in ref. 3.
In addition to this, the size, shape and solid phase (or crystallinity) of a nanoparticle are important factors associated with the potential for toxicity.22–25 The reactive surfaces of nanocatalysts can produce free radicals that can be damaging to humans and the environment.22,23,26 The most catalytically active particles can also be the most toxic, but this can change as the shape evolves in response to changes in the local environment. It is unlikely that we will be able to engineer nanoparticles that deliver superior performance while also being entirely safe, so once again it is critical that we are able to exercise control over the morphology.
The first step in controlling or preventing these transformations involves constructing a detailed understanding of the nanomorphology (size, shape and phase) of ZnS nanoparticles, and how they interact and change in response to their surroundings.25 This can be difficult to achieve experimentally, since the thermodynamic behaviour of nanomaterials differs from materials on larger scales (bulk materials). This is due to significant contributions from the free energy associated with geometric features containing under-coordinated atoms27,28 (such as surfaces, edges and corners) which represent little more than a minor energetic perturbation in the bulk.29 For example, experimental work has shown that the structure of small ZnS nanoparticles may differ significantly from the bulk, and while they can adopt a highly distorted structure, they are not completely disordered, and often contain a mixture or crystalline and amorphous atomic arrangements.13 Since stepwise observations are not possible experimentally, and analysis of all possible sizes, shapes and configurations is unfeasible, understanding the stability of these nanoparticles remains a challenge.
For this reason, theoretical and computational approaches are ideal, since they facilitate the rapid assessment of a large number of physical parameters simultaneously. However, one of the greatest challenges in modelling systems such as these is the accurate inclusion of realistic amorphous materials. In the case of ZnS nanoparticles, experimental studies have revealed that nanoparticles often adopt a core–shell structure, and the ratio of amorphous shell to crystalline core may vary depending on the size of the particle.13 Investigating the role of core–shell crystalline/amorphous structures is important when attempting to identify the phase relationships in this system, so we turn to multi-scale theoretical treatments to avoid the ambiguity associated with purely computational models that may or may not overcome the energy barriers surrounding the thermodynamically preferred form.
Presented here are results of first principle computer simulations and advanced theoretical modelling used to investigate the relationship between size and shape in determining the crystallinity of ZnS nanoparticles. We find that the lowest energy shape of zinc blende nanoparticles is a rhombic dodecahedron, enclosed entirely by stoichiometric (non-polar) {220} facets. However, we also find that the introduction of higher energy (polar) facets, possibly via kinetic processes, has an important effect on the size-dependent transformation between ZB, amorphous and core–shell crystalline/amorphous nanoparticles, as well as the agglomeration behaviour of dry samples.
Theoretical and computational methods
At standard temperature and pressure (STP) ZnS is stable in the zinc-blende (ZB or B3) phase, otherwise known as sphalerite. The ZB phase possesses a dual basis, face-centred cubic structure with an internal parameter of (¼, ¼, ¼). Both zinc and sulfur atoms are tetrahedrally coordinated and the ZnS dimers are stacked in an ABCABC arrangement. In the present study we have calculated the specific surface energies for the {200}, {111}, {220} and {311} surfaces as they are often observed experimentally in samples of ZB ZnS nanoparticles.30–34The properties of these surfaces have been calculated using Density Functional Theory (DFT) within the Generalized-Gradient Approximation (GGA) with the Perdew and Wang (PW91)35 exchange-correlation functional, implemented via the Vienna ab initio Simulation Package (VASP).36,37 We have used the Linear Tetrahedron Method (LTM) and Projected Augmented Wave (PAW) potentials38,39 for both the initial structural relaxations and reconstructions, and the final static (single point) calculations required for accurate free energies and surface stress tensors. The electronic relaxation technique used here is an efficient matrix diagonalization routine based on a sequential band-by-band residual minimization method of single-electron energies,40,41 with direct inversion in the iterative subspace, whereas the ionic relaxation involves minimization of the Hellmann–Feynman forces, to an energy convergence of 10−4 eV. These methods and criteria have been rigorously tested, and found to provide the optimal balance between accuracy and computational efficiency, and bulk properties in agreement with experiment.42
Amorphous ZnS was produced by expanding and heating (using NVT molecular dynamics) a 3 × 3 × 3 supercell of crystalline ZB structured ZnS, containing 216 atoms. The volume of the supercell was initially expanded to ∼20% above its equilibrium value, then thermally annealed in various stages up to 1500 K, and finally quenched down to 300 K. NVE molecular dynamics was then conducted until the system reached thermal equilibrium. Once thermal equilibrium was obtained the volume of the supercell was uniformly contracted in stages, allowing for full atom relaxation at each stage, to determine the equilibrium volume. A radial distribution function of the system at equilibrium mass density was then calculated and showed a very diffuse second order peak and no definitive structure at long range indicating the system had amorphised.
From the amorphous bulk a vacuum space of approximately 30 Å was created to form an amorphous slab. This slab was then relaxed by successive molecular dynamics/geometry optimisation runs to fully relax the surface layers. Throughout the amorphisation procedure the initial molecular dynamics calculations were conducted using the Lattice program GULP43 and the force field potential described in ref. 44. Subsequent molecular dynamics and all geometry optimisations were conducted using DFT. For the geometry optimisations we used the same methodology as for crystalline ZnS calculations except that the k-point sampling was reduced to 2 × 2 × 2 or 2 × 2 × 1 for the bulk and surface runs respectively. Testing at higher k-point sampling resolution showed the total energy was the same as for 2 × 2 × 2 to within a few meV (the energy resolution of the VASP code).
Surface structure and energetics
The surface formation energy γi (for a surface in orientation i), can be defined in terms of µZnS,bulk, the chemical potential of bulk ZnS (in the ZB structure) as follows: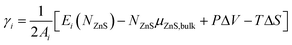 | (1) |
In each case a stoichiometric two dimensional slab was generated comprising of 20 atomic layers, surrounded by 20 Å of vacuum space perpendicular to the crystallographic plane of interest (i), and the entire structure was fully reconstructed and relaxed prior to the calculation of the energy and stress. The terminal layer of the {220} surface contains both Zn and S atoms (see Fig. 1(a)). However, in the case of the {111}, {200} and {311} surfaces (see Fig. 1(b)–(d), respectively), one surface is terminated by a layer of Zn atoms, and the other by a layer of S atoms. It is possible to unambiguously define the specific surface energies of these unique surfaces in terms of the chemical potentials of the constituents (µZn and µS), however, when investigating the shape of regular (symmetric) nanocrystals the total surface energy difference does not depend on µZn or µS, and the sum of the surface energies of polar surfaces is always a constant. This is a consequence of the fact that both surfaces must be present on the nanocrystal to preserve the stoichiometry of the entire nanoparticle. Therefore, in the present study, we have used an “average value” of surface energy for the {111}, {200} and {311} surfaces. A comparison of our results of the surface formation energies γi, i = 200, 111, 220 and 311, is provided in Table 1, along with some previously reported polar surfaces (that are not directly comparable).
| Method | {220} | {111} | {200} | {311} | AM | INT |
|---|---|---|---|---|---|---|
| a Ref. 44. b Ref. 45. c Ref. 46. d This study. e Zn-Terminated. f S-Terminated. g Averaged over Zn- and S-terminated. | ||||||
| Lattice statics simulation, IAPa | 0.53 | 1.01,e 0.87f | 1.12,e 1.30f | |||
| DFT, GGA (PW91)a | 0.46 | |||||
| MDb | 0.65 | 1.82,e 1.12f | 1.25,e 1.31f | |||
| MDc | 0.39 | 1.84 | 2.56 | |||
| DFT, GGA (PW91)d | 0.43 | 1.36g | 2.03g | 1.73 | 0.28 | 0.06 |
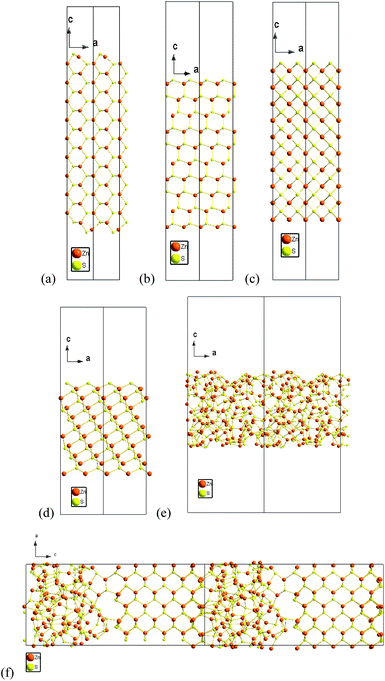 | ||
| Fig. 1 Schematic representations of the stoichiometric 2-dimensional zinc blende periodic slabs following relaxation using DFT. Each slab is oriented perpendicular to (a) the 〈220〉 direction, (b) the 〈111〉 direction, (c) the 〈200〉 direction, and (d) the 〈311〉 direction, and separated by a 2 nm vacuum layer. Also shown is (e) the 2-dimensional amorphous slab, and (f) the combined ZB/amorphous structure used to calculate the interfacial energy and stress. | ||
In the case of the amorphous ZnS surface, a series of calculations were undertaken to sample a range of amorphous structures, in order to find the lowest energy average. The surface energy was calculated using eqn (1), but with the chemical potential for a bulk amorphous structure in the second term (as well as a amorphous surface slab in the first term). The interfacial energy was calculated by simply subtracting NZnS,ZBµZnS,ZB + NZnS,AMµZnS,AM from the combination structure, where µZnS,ZB and µZnS,AM are the chemical potentials of the ZB and amorphous bulk materials, and NZnS,ZB and NZnS,AM are the number of ZnS formula units in the combination structure occupying zinc blende and amorphous configurations, respectively.
The isotropic surface stresses σi were computed from the trace of the surface stress tensor, which is output directly by the VASP code. No previous results could be located for comparison with the calculated values of σ200 = 0.19 J m−2, σ111 = −0.49 J m−2, σ220 = 0.41 J m−2, σ311 = 0.37 J m−2 and σamorphous= −0.03 J m−2.
Thermodynamics and nanomorphology
Modelling of the three dimensional polyhedra has been achieved using a shape-dependent thermodynamic model based on a geometric summation of the Gibbs free energy.28,47 A truncated version of the model has been used here, that is applicable specifically to isolated, defect-free structures in the range ∼3 to 100 nm, as described in ref. 28. In this version the total free energy G is described in terms of the specific surface free energies γi, for facets i, weighted by the factors fi (such that ∑ifi = 1):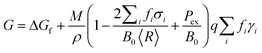 | (2) |
This methodology has been previously used to successfully model the shape of CdS48 and FeS2,49–52 but is important to point out that these quantities were calculated at zero temperature. This means that G is effectively a free energy of formation that is equivalent to the enthalpy for formation, but it also has implications for the applicability of the model results to real experiments. Our model results are more consistent with low-temperature quasi-equilibrium conditions, and consequently have limited applicability to cases where ZnS nanostructures are grown at high temperature.
Discussion of results
Using the values of γi provided in Table 1, and σi as listed above, we modelled the energy of a collection of shapes enclosed by different combinations of these low index surfaces, as shown in Fig. 2. In this collection, four morphologies are enclosed entirely by one type of surface, presenting as the Catalan rhombic dodecahedron (Fig. 2(a)), the Platonic octahedron (Fig. 2(b)), the Catalan deltoidal icositetrahedron (Fig. 2(c)), and the Platonic regular hexahedron (Fig. 2(d), also know as the cube). These shapes are enclosed by {220}, {111}, {311} and {200} facets, respectively.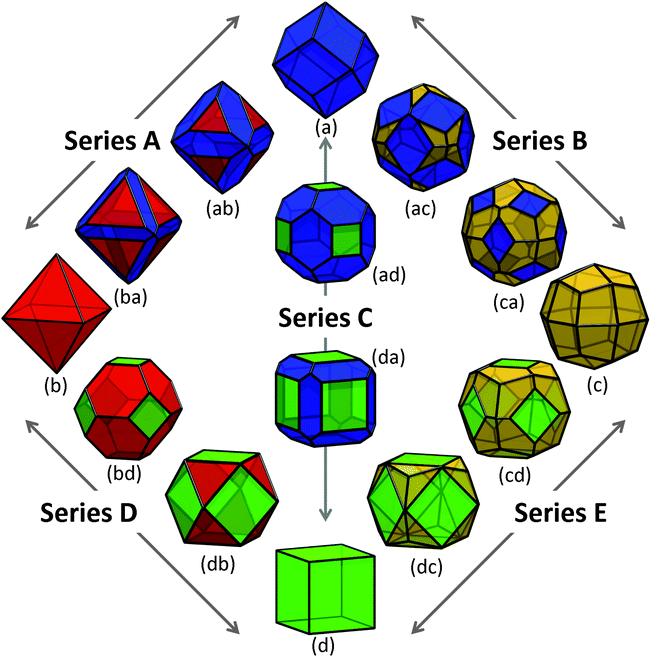 | ||
| Fig. 2 Shapes of zinc blende ZnS nanoparticles explored in this study, with truncation series terminated by (a) the Catalan rhombic dodecahedron, (b) the Platonic regular octahedron, (c) the Catalan deltoidal icositetrahedron, and (d) the Platonic regular hexahedron (or cube). The stationary points in each series are chosen such that the fraction of surface area attributed to the minority and/or majority facets conform to the ratio defined by the Platonic truncated octahedron (bd) and Archimedian cuboctahedron (db). The {220} facets are shown in blue, {111} facets are shown in red, {311} facets are shown in yellow, and {200} facets are shown in green. | ||
The free energies for the more complicated shapes (those enclosed by more than one type of surface) have also been calculated, and are presented in Fig. 3, with respect to bulk ZnS. Here we see that, although a small truncation has the effect of lowering the surface-to-volume ratio, the degree of surface energy anisotropy is significant, and a departure from the ideal polyhedra is still thermodynamically unfavourable unless only lower energy facets are introduced. For example, irrespective of the direction of truncation the rhombic dodecahedron remains the lowest energy shape, since (although Fig. 2(ab), (ac) and (ad) have lower surface-to-volume ratios) all other facets are significantly higher in energy than the {220}. However, if we were to begin at the bottom of Fig. 2, with the regular hexahedron 2(d), then the modifications of the shape that introduce additional {111}, {220} and {311} facets (shown in Fig. 2(db), (da) and (dc), respectively) both lower the surface-to-volume ratio and the total surface energy. As a rule of thumb, truncation of the hexahedron is always favourable, and truncation of the other high energy shapes depends sensitively on the relative energy of the different facets and the degree of truncation. This is not to say that higher energy shapes (such as those in Fig. 2, or other combinations not included in this study) cannot form, merely that these shapes are thermodynamically unfavourable with respect to a morphological transformation to a rhombic dodecahedron. The transformation may or may not be spontaneous depending upon the kinetic barriers present, and the driving force applied.
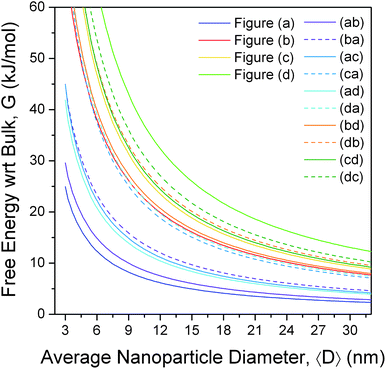 | ||
| Fig. 3 Relative free energy of formation of zinc blende structured zinc sulfide nanoparticles, as a function of size and shape, showing the rhombic dodecahedron (a) is the thermodynamically preferred shape, and the regular hexahedron the least preferred. The shapes are defined in Fig. 2, and the results are calculated with respect to bulk ZB ZnS. | ||
These results will have implications for the way ZB ZnS nanoparticles interact with their surroundings (and each other). The {220} facets are non-polar and will interact via weak van der Waals forces (see Fig. 1(a)). The {111}, {331} and {200} facets are polar (see Fig. 1(b)–(d)), and if introduced kinetically, will allow the nanoparticles to interact via stronger electrostatic attraction and repulsion. The former gives rise to loosely bound aggregates or isolated particles given suitable perturbation, whereas the latter are stronger interactions that are often associated with self-assembly or the formation of robust ordered superstructures.53 This will influence the agglomeration behaviour, and hence the bioavailability of dry samples.
These results are in good agreement with those reported previously,44,54,55 based on lattice statics simulations and DFT,44 where large ZnS ZB particles were found to prefer rhombic dodecahedral morphologies. At smaller sizes, Spano et al.55 estimated the global energy minimum of small, individual ZnS structures ranging in size from 10 to 47 atoms. Using simulated annealing method and a classical inter-atomic potential (supported by DFT), these explicit calculations produced ‘bubble’ clusters (appearing as hollow structures consisting of 4, 6 and 8 atom rings), where all the atoms in the structure are three-fold coordinated, as opposed to the tetrahedral four-fold coordination encountered in “larger” structures (which are still much smaller than those observed experimentally). Similar studies of n = 50 to 80 produced onion-like structures, where one bubble cluster was enclosed inside another with tetrahedral bonding between the two.54,55
This is similar to the formation of core–shell bucky-diamond structures which is well known in carbon,56,57 and is attributed to delamination of the (111) facets. Again, a change in shape will promote or suppress this instability. At still larger sizes it has been suggested (from MD simulations) that the BCT phase gains stability n > 80.58 This is also likely to be highly dependent on the shape of the particles, as observed in other tetrahedrally coordinated semiconductors.59,60
Size-dependent crystallinity
In addition to morphological instability introduced by the presence of high energy facets, or kinetically grown shapes, ZnS may also undergo solid–solid phase transformation under ambient conditions. Zhang et al. observed reversible structural transformations in ZnS nanoparticles at room temperature,13 induced by aggregation–disaggregation and absorption–desorption of methanol and water. It was therefore suggested that water decreases the surface free energy, and promotes crystallinity throughout the nanoparticles. These studies were complemented by classical MD simulations of the interaction between methanol and water and the surface S and Zn ions, which showed that the surfaces of nanoparticles in methanol undergo reconstruction that penetrates several atomic layers, leading to a crystalline core surrounded by a disordered shell. However, insufficient structures were sampled in this study to definitively attribute the emergence of the core–shell structure as a byproduct of surface chemical reactions, and it cannot be ruled out that crystalline/amorphous core–shell structures are simply more energetically favourable at small sizes.Depending upon the number of atomic layers participating in the amorphous shell a core–shell particle will consist of differing volumetric ratios of ZB and amorphous materials, as well as a free amorphous surface and a ZB/amorphous interface (Table 1, INT), all of which scale with size. If the change in the surface and interfacial free energy provides the driving force for a change in degree of crystallinity, then it follows that the various size-dependent free energies and energy differences (which is dominated by the surface energy term at small sizes) will also play an important role, irrespective of the chemical environment.
To investigate this issue, we have used the same theoretical and computational method described above to calculate the properties of amorphous ZnS (see Fig. 1(e)), and a ZB/amorphous interface (see Fig. 1(f)), and used them to calculate the free energy of core–shell nanoparticles with different ZB/amorphous volumetric ratios (see Fig. 4(a)–(e)), along with a complete amorphous ZnS spherical nanoparticle (Fig. 4(f)), to compare with low energy ZB structures over 2 nm in size. The core–shell particles were modelled by subtracting the volume of the crystalline core from the centre of the amorphous sphere, and adding a ZB core enclosed by the {220} interfaces characterised by the interfacial energy as defined above (and in Table 1). Each region has retained the characteristic bulk modulus, bulk density and bulk formation energy.
 | ||
| Fig. 4 The ZB crystalline/amorphous core–shell structures modelled in this study, with (a) 82.0% ZB and 18.0% amorphous ZnS by volume, (b) 57.6% ZB and 42.4% amorphous ZnS by volume, (c) 38.6% ZB and 61.4% amorphous ZnS by volume, (d) 24.3% ZB and 75.7% amorphous ZnS by volume, (e) 14.1% ZB and 85.9% amorphous ZnS by volume, and (f) the 100% amorphous ZnS by volume. | ||
The appropriate choice of the bulk free energy of formation, ΔGf, for both the ZB and amorphous materials, is an important aspect of this analysis. In general, the free energy is the energy difference from reaction that may include a variety of reactants and products. The final value depends upon the temperature and the species participating in the chemical reaction, since some reactions are more favourable than others. For example, experimental values for the bulk ZB enthalpy of formation are −206.53 kJ mol−1 as measured by Deore and Navrotsky,61 between −21.87 and −105.45 kJ mol−1 by Daskalakis and Helz,62 and between −18.84 and −30.26 kJ mol−1 by Hayashi et al.63 For amorphous ZnS an experimental value for the bulk free energy of formation can vary between −33.52 and −62.87 kJ mol−1, as shown by Gubeli and Marie.64 In order to accurately compare the free energy difference between ZB and amorphous ZnS it is necessary to ensure that the same reaction is considered, but this is problematic since a single reaction rarely produces two different ZnS products. None of these values originate from identical reactions. Therefore, we have calculated these value by subtracting the energy per ion of Zn in the hexagonal phase and S in the S8 dimer from the average Zn–S bond energy determined from our ZB and amorphous supercells, so that they are both calculated using the same computational method (as described above) and reaction, (ZnS)8 = (Zn)8 + S8. This gave a value of −166.28 kJ mol−1 for bulk ZB ZnS and −116.47 kJ mol−1 for bulk amorphous ZnS, with a free energy difference of 49.78 kJ mol−1. Based on the values mentioned and referenced above, the experimental difference (for a “like-reaction”) is approximately 44.53 kJ mol−1. It is possible that the discrepancy is due to configurational entropy. While the configurational entropy of amorphous materials may be non-negligible, there is no feasible way of including the exact configurational entropy computationally. Experimental results are always a statistical average, so one may decide to repeat simulations of model structures and average over different computational images. However, one may only recover the exact solution when an infinite number of images have been included. In our case, we have used a single converged image because the uncertainties introduced by this approximation are less than the uncertainty inherent in the nanomorphology model (estimated by sampling different images during the geometric optimization, as described above).
Using the surface free energies, isotropic surface stresses and bulk properties outlined above, the total free energy for the low energy ZB shapes (which now include the bulk free energy of formation) has been compared to spherical amorphous nanoparticles and crystalline/amorphous core–shell structures using eqn (2). These results are provided as a function of molar surface area in Fig. 5, and predict that a size-dependent phase transformation may be expected in the range 3.9 nm to 14.2 nm, depending upon the degree of morphological dispersion and core–shell ratio. For example, the second lowest energy shape (Fig. 2(ab)) exhibits a crossing with the thinnest shell structure (Fig. 4(a)) at 8.4 nm, and we find that at smaller sizes thicker shells are more favourable than a purely ZB structure with this morphology. This suggests that, at small sizes, the surfaces of higher energy shapes will more readily amorphize, even though they are still dominated by low energy {220} facets. These results are in agreement with experimental observations of ZnS nanoparticles reported in the literature13 and clearly show how nanoparticle shape and core-structure are intrinsically linked. Over 14.2 nm the core–shell structure is not stable, irrespective of the core–shell ratio or crystal habit, in agreement with macroscopic observations.1
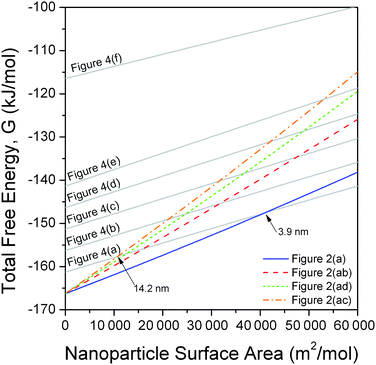 | ||
| Fig. 5 Relative free energy of formation of low energy shapes of zinc blende structured zinc sulfide nanoparticles (as defined in Fig. 2), as a function of surface area, compared to the free energy of formation of a core–shell crystalline/amorphous ZnS nanoparticle (as defined in Fig. 4) and an amorphous ZnS sphere. The crossovers indicate a size dependent phase transformation given a suitable kinetic perturbation. | ||
The higher energy shapes (not shown in Fig. 5) are not expected to be stable at any size, since although a transformation from amorphous to crystalline is expected between ∼15 nm and 60 nm in size, there are a much larger number of mechanistic pathways to facilitate changes in both shape and phase. In general, the height of any kinetic barrier will depend intimately on the mechanistic pathway adopted by atoms during any phase transition, and while a crystalline-to-amorphous transition may only require small local motion, a crystalline-to-crystalline transition could necessitate a large change in shape and hence present a much larger kinetic barrier. In this case any driving force sufficient to overcome the crystalline-to-crystalline morphological transformation barrier will be sufficient to invoke a simultaneous transformation to an amorphous nanoparticle along the way. Therefore, in general, size-dependent transformations between zinc blende and crystalline/amorphous core–shell nanoparticles may only be controlled (or avoided) if sensitive control over the shapes can be achieved. These results also demonstrate that these phase transformations are highly exothermic. This is the first time this technique has been used to model amorphous nanoparticles, and to identify the size-dependent changes in crystallinity.
Although these results are enlightening a number of questions remain, including the dependence on stoichiometry and surface chemistry, and the relative stability of the wurtzite form of ZnS. We expect both factors will impact the transformation size to some degree. Fujiwara, Hosokawa, Kanemoto, Murakoshi, Wada, Yanagida and others investigated some of these issues,14,15,65,66 as well as the interaction of surfaces with organic solvents.67,68 In particular, Hosokawa et al.67 found that zinc atoms on the surface facets were solvated by the oxygen atoms in dimethylformamide (DMF, a common organic solvent used in ZnS nanoparticle production) and that the choice of zinc salt (the source of zinc) affected the coordination of the surface atoms thus affecting the efficiency of the DMF as a solvent, leading to varying degrees of surface stoichiometry. This suggests that, in addition to size control, moderating the supersaturation of S and/or the adsorption of oxygen containing groups (such as water) may provide an avenue for engineering the morphology of ZnS nanoparticles, or a way of anticipating their relative stability under different environmental conditions. This is a topic for future work, as is a parameterisation of the model for wurtzite structured ZnS, as it has been shown to be an important constituent of the ZnS phase relationship at small sizes.46
Conclusions
Nanomorphology prediction remains one of the most coveted but complex aims of nanotechnology today, one that will facilitate the design of nanomaterials in a way that is not currently available. However, these results highlight how creating designer morphologies involves more than just controlling the shape, we must also pay attention to consequential structural instabilities, such as changes in crystallinity. Although some desirable sizes and shapes may deliver superior properties, they may not be sufficiently stable to ensure this benefit is maintained long term.In this paper we have shown using first principles computer simulations and analytical modelling that the shape of zinc blende ZnS nanoparticles and the core–shell structure and mixing ratio of crystalline/amorphous particles has an important impact on the thermodynamic stability of this nanomaterial. Future work in this area will be directed toward understanding how this stability is affected by changes in the supersaturation of sulfur, the presence of water, and the existence of alternative transformation pathways afforded by the wurtzite phase.
Acknowledgements
C.A.F. acknowledges support from the Australian Research Council APA and the CSIRO PhD Scholarship Program. A.S.B acknowledges support from the Australian Research Council under DP0986752. Computational resources for this project have been supplied by NCI under the MAS application scheme (project k76).Notes and references
- X. Fang, Y. Bando, U. K. Gautam, T. Zhai, H. Zeng, X. Xu, M. Liao and D. Golberg, Crit. Rev. Solid State Mat. Sci., 2009, 34, 190–223 Search PubMed.
- E. Monroy, F. Omnes and F. Calle, Semicond. Sci. Technol., 2003, 18, 33 CrossRef.
- C. Feigl, S. P. Russo and A. S. Barnard, J. Mater. Chem., 2010, 20, 4971 RSC.
- X. S. Fang, C. H. Ye, L. D. Zhang, Y. H. Wang and Y. C. Wu, Adv. Funct. Mater., 2005, 15, 63–68 CrossRef CAS.
- J. H. He, Y. Y. Zhang, J. Liu, D. Moore, G. Bao and Z. L. Wang, J. Phys. Chem. C, 2007, 111, 12152–12156 CrossRef.
- X. Fang, Y. Bando, M. Liao, U. K. Gautam, C. Zhi, B. Dierre, B. Liu, T. Zhai, T. Sekiguchi, Y. Koide and D. Golberg, Adv. Mater., 2009, 21, 2034–2039 CrossRef CAS.
- P. Löw, B. Le Pioufle, B. Kim and C. Bergaud, Sens. Actuators, B, 2008, 130, 175–180 CrossRef.
- Z. G. Chen, J. Zou, G. Liu, H. F. Lu, F. Li, G. Q. Lu and H. M. Cheng, Nanotechnology, 2008, 19, 055710 CrossRef.
- X. S. Fang, Y. Bando, G. Z. Shen, C. H. Ye, U. K. Gautam, P. M. F. J. Costa, C. Y. Zhi, C. C. Tang and D. Golberg, Adv. Mater., 2007, 19, 2593–2596 CrossRef CAS.
- B. Walker, A. B. Tamayo, X.-D. Dang, P. Zalar, J. H. Seo, A. Garcia, M. Tantiwiwat and T.-Q. Nguyen, Adv. Funct. Mater., 2009, 19, 3063–3069 CrossRef CAS.
- B. O. Dabbousi, J. Rodriguez-Viejo, F. V. Mikulec, J. R. Heine, H. Mattoussi, R. Ober, K. F. Jensen and M. G. Bawendi, J. Phys. Chem. B, 1997, 101, 9463–9475 CrossRef CAS.
- X. G. Peng, M. C. Schlamp, A. V. Kadavanich and A. P. Alivisatos, J. Am. Chem. Soc., 1997, 119, 7019–7029 CrossRef CAS.
- H. Z. Zhang, B. Gilbert, F. Huang and J. F. Banfield, Nature, 2003, 424, 1025–1029 CrossRef CAS.
- K. Murakoshi, H. Hosokawa, N. Tanaka, M. Saito, Y. Wada, T. Sakata, H. Mori and S. Yanagida, Chem. Commun., 1998, 21–322 RSC.
- K. Murakoshi, H. Hosokawa and S. Yanagida, Jpn. J. Appl. Phys., 1999, 38, 522–527 CrossRef CAS.
- Y. W. Pan, J. Yu, Z. Hu, H. D. Li, Q. L. Cui and G. T. Zou, J. Mater. Sci. Technol., 2007, 23, 193–195 CAS.
- S. Li, J. S. Lian and Q. Jiang, Chem. Phys. Lett., 2008, 455, 202–206 CrossRef CAS.
- C. Z. Yang, Y. G. Liu, H. Y. Sun, D. F. Guo, X. H. Li, W. Li, B. T. Liu and X. Y. Zhang, Nanotechnology, 2008, 19, 095704 CrossRef.
- F. Huang, B. Gilbert, H. H. Zhang and J. F. Banfield, Phys. Rev. Lett., 2004, 92, 4.
- B. Gilbert, H. Z. Zhang, F. Huang, J. F. Banfield, Y. Ren, D. Haskel, J. C. Lang, G. Srajer, A. Jurgensen and G. A. Waychunas, J. Chem. Phys., 2004, 120, 11785–11795 CrossRef CAS.
- B. Gilbert, F. Huang, Z. Lin, C. Goodell, H. Z. Zhang and J. F. Banfield, Nano Lett., 2006, 6, 605–610 CrossRef CAS.
- G. Oberdorster, E. Oberdorster and J. Oberdorster, Environ. Health Perspect., 2005, 113, 823–839 CrossRef CAS.
- M. F. Hochella, S. K. Lower, P. A. Maurice, R. L. Penn, N. Sahai, D. L. Sparks and B. S. Twining, Science, 2008, 319, 1631–1635 CrossRef.
- A. S. Barnard, Nat. Mater., 2006, 5, 245 CrossRef CAS.
- A. S. Barnard, Nanoscale, 2009, 1, 89 RSC.
- A. S. Barnard, Nat. Nanotechnol., 2009, 4, 332 CrossRef CAS.
- G. Wulff, Z. Kristallogr., 1901, 34, 449–530 CAS.
- A. S. Barnard, J. Phys. Chem. B, 2006, 110, 24498–24504 CrossRef CAS.
- E. S. Machlin, An Introduction to Aspects of Thermodynamics and Kinetics Relevant to Materials Science, Elsevier, 3rd edn, 2007 Search PubMed.
- H. Tong, Y.-J. Zhu, L.-X. Yang, L. Li, L. Zhang, J. Chang, L.-Q. An and S.-W. Wang, J. Phys. Chem. C, 2007, 111, 3893–3900 CrossRef CAS.
- L. P. Wang and G. Y. Hong, Mater. Res. Bull., 2000, 35, 695–701 CrossRef CAS.
- J. Xu and W. Ji, J. Mater. Sci. Lett., 1999, 18, 115–117 CrossRef CAS.
- X. Ye, W. Zhuang, Y. Fang, Y. Hu, K. Zhao and X. Huang, Mater. Chem. Phys., 2008, 112, 730–733 CrossRef CAS.
- N. Saravanan, G. B. Teh, S. Y. P. Yap and K. M. Cheong, J. Mater. Sci.: Mater. Electron., 2008, 19, 1206–1208 CrossRef CAS.
- J. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, RC558 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- D. M. Wood and A. Zunger, J. Phys. A: Math. Gen., 1985, 18, 1343 CrossRef CAS.
- See ESI†.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291 CrossRef CAS.
- S. Hamad, S. Cristol and C. R. A. Catlow, J. Phys. Chem. B, 2002, 106, 11002–11008 CrossRef CAS.
- K. Wright, G. W. Watson, S. C. Parker and D. J. Vaughan, Am. Mineral., 1998, 83, 141 CAS.
- H. Z. Zhang, F. Huang, B. Gilbert and J. F. Banfield, J. Phys. Chem. B, 2003, 107, 13051–13060 CrossRef CAS.
- A. S. Barnard and P. Zapol, J. Chem. Phys., 2004, 121, 4276 CrossRef CAS.
- A. S. Barnard and H. Xu, J. Phys. Chem. C, 2007, 111, 18112 CrossRef CAS.
- A. S. Barnard and S. P. Russo, J. Phys. Chem. C, 2007, 111, 11742 CrossRef CAS.
- A. S. Barnard and S. P. Russo, Nanotechnology, 2009, 20, 115702 CrossRef.
- A. S. Barnard and S. P. Russo, J. Phys. Chem. C, 2009, 113, 5376 CrossRef CAS.
- A. S. Barnard and S. P. Russo, J. Mater. Chem., 2009, 19, 3389 RSC.
- A. S. Barnard, J. Mater. Chem., 2008, 18, 4038 RSC.
- S. Hamad, C. Richard, C. R. A. Catlow, E. Spano, J. M. Matxain and J. M. Ugalde, J. Phys. Chem. B, 2005, 109, 2703–2709 CrossRef CAS.
- E. Spano, S. Hamad and C. R. A. Catlow, Chem. Commun., 2004, 864–865 RSC.
- F. Banhart, Rep. Prog. Phys., 1999, 62, 1181–1221 CrossRef CAS.
- A. S. Barnard and M. Sternberg, J. Mater. Chem., 2007, 17, 4811 RSC.
- S. Hamad and C. R. A. Catlow, J. Cryst. Growth, 2006, 294, 2 CrossRef CAS.
- B. J. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 174105 CrossRef.
- Y. Wu, G. Chen, H. Ye, Y. Zhu and S.-H. Wei, Appl. Phys. Lett., 2009, 94, 253101 CrossRef.
- S. Deore and A. Navrotsky, Am. Mineral., 2006, 91, 400–403 CrossRef CAS.
- K. D. Daskalakis and G. R. Helz, Geochim. Cosmochim. Acta, 1993, 57, 4923 CrossRef CAS.
- K. Hayashi, A. Sugaki and A. Kitakaze, Geochim. Cosmochim. Acta, 1990, 54, 715 CrossRef CAS.
- A. O. Gubeli and J. Ste. Marie, Can. J. Chem., 1967, 45, 2101 CrossRef.
- M. Kanemoto, H. Hosokawa, Y. Wada, K. Murakoshi, S. Yanagida, T. Sakata, H. Mori, M. Ishikawa and H. Kobayashi, J. Chem. Soc., Faraday Trans., 1996, 92, 2401 RSC.
- H. Fujiwara, H. Hosokawa, K. Murakoshi, Y. Wada and S. Yanagida, Langmuir, 1998, 14, 5154 CrossRef CAS.
- H. Hosokawa, K. Murakoshi, Y. Wada, S. Yanagida and M. Satoh, Langmuir, 1996, 12, 3598 CrossRef CAS.
- H. Fujiwara, K. Murakoshi, Y. Wada and S. Yanagida, Langmuir, 1998, 14, 4070 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Testing of DFT, DFT parameters and convergence criteria used in this study, and bulk zinc blende ZnS properties. See DOI: 10.1039/c0nr00417k |
| This journal is © The Royal Society of Chemistry 2010 |
