Use of spin traps to measure the addition and fragmentation rate coefficients of small molecule RAFT-adduct radicals†
Elena
Chernikova
*a,
Vladimir
Golubev
a,
Anatoly
Filippov
a,
Ching Yeh
Lin
b and
Michelle L.
Coote
*b
aLenin Hills, 1, bld. 3, Polymer Department, Faculty of Chemistry, Lomonosov Moscow State University, Moscow, 119991, Russia. E-mail: chernikova_elena@mail.ru; Fax: +7 495 9390174; Tel: +7 495 9395409
bARC Centre of Excellence for Free-radical Chemistry and Biotechnology, Research School of Chemistry, Australian National University, Canberra, ACT 0200, Australia. E-mail: mcoote@rsc.anu.edu.au; Fax: +61 2 6125 0750
First published on 6th September 2010
Abstract
Spin traps have been used to obtain the first direct experimental determination of the addition (5 × 106 L mol−1 s−1), fragmentation (8 × 10−3 s−1) and self-termination (6.5 × 102 L mol−1 s−1) rate coefficients in RAFT polymerization using the interaction of a tert-butyl radical with tert-butyl dithiobenzoate at ambient temperature as a model reaction.
Since the invention of the addition fragmentation chain-transfer (RAFT) polymerization process,1 there has been an ongoing debate about the origin of retardation and inhibition effects in polymerizations mediated by cumyl dithiobenzoate and related dithiobenzoate agents.2,3 On the one hand, a kinetic model that assumes that intermediate radical cross- and self-termination reactions (IRT) occur with diffusion-controlled rate coefficients, similar to those for the bimolecular termination of conventional propagating polymer radicals (i.e. <kt> < ca. 107–108 L mol−1 s−1), can be fitted successfully to experimentally determined overall reaction rates and ESR-derived radical concentrations.4 However, this so-called IRT model predicts that significant concentrations of the IRT products should be produced even under standard RAFT conditions and these are not observable in significant quantities in the resulting polymer except under forcing conditions.5 Furthermore, the fragmentation rate coefficient (kfr = 104 s−1) and equilibrium constants (K = kad/kfr = 55 mol L−1, where kad is the rate coefficient for addition) that are obtained under the IRT model are incompatible with those predicted from quantum chemistry,6 with radical storage experiments,7 and with the kinetics of thioketone mediated polymerization.8 Many of these problems can be addressed if one instead assumes that IRT is not kinetically significant under normal polymerization conditions (i.e., <kt> < ca. 104 L mol−1 s−1). In this case, model fitting to experimental kinetic data indicates that the intermediate radicals are much more stable (K = 1.06 × 107 L mol−1) and there is no significant IRT product formation.6c,9 However, this so-called slow fragmentation model also predicts intermediate radical concentrations that are completely incompatible with the available ESR data, measured for polymerizing systems. Resolving these inconsistencies and finding the correct kinetic model for RAFT polymerization would improve our understanding of the process and assist in process optimization and control.
Various proposals have been made to reconcile these conflicting observations. Buback et al.10 have suggested that the absence of IRT products could be explained if the IRT product reacts with another propagating radical to form a terminated chain and re-form the intermediate radical; however, direct evidence for the existence of this reaction has yet to be provided. Moreover, such a revised IRT model still predicts fragmentation rates and equilibrium constants that are incompatible with the results from quantum chemistry, with radical storage experiments and thioketone-mediated polymerization. In a further alternative, Konkolewicz et al.11 recently suggested that all incompatible observations might be reconciled by allowing for a strongly chain length dependent version of the IRT model with concomitant slow fragmentation; however, the physical basis for such strong chain length effects has been questioned in the literature.3 This is not to say that either of these proposals are incorrect, rather more evidence is required, preferably based on direct experimental measurements of model compounds.3
To date, experimental measurements of the individual rate coefficients have taken place within the context of a polymerizing system and have necessarily involved the fitting of some type of assumed kinetic model to the experimental data. As illustrated above, these kinetic assumptions can have a large influence on the resulting estimated parameters. In that regard, the use of quantum chemistry is particularly attractive as, unlike experiments, such calculations depend only on the laws of quantum mechanics and the numerical approximations that are introduced to solve the resulting equations. However, since the accuracy of such calculations can vary considerably with the level of theory chosen, external experimental benchmarking is important. Experimentally, one can reduce the dependence on model-based assumptions by carrying out experiments in situations where the kinetic effects of these assumptions are minimal, or by studying the reactions in isolation, usually on much simpler model compounds. A promising example of the former approach is a laser flash photolysis technique recently introduced by Buback et al. and used to measure the fragmentation rate and equilibrium constants for S–S′-bis(methyl-2-propionate)-trithiocarbonate mediated polymerization of butyl acrylate in toluene at −30 °C.12 It is worth noting that results generated in this study, which were shown to be insensitive to the assumed rate of IRT termination, are in very good agreement with the quantum-chemical calculations.13 However, this experimental technique has not as yet been applied to the more controversial dithiobenzoate mediated polymerizations as the dithiobenzoate chromophore absorbs in the UV region and undergoes photo-induced decomposition. To study these systems an alternative approach is required.
To this end, in the present work we use a spin trapping technique based on electron spin resonance (ESR) spectrometry to study the kinetics and mechanism of the elementary steps of RAFT polymerization. Spin traps are strong inhibitors of radical reactions; hence they are useful when the need arises to examine processes involving unstable radicals in a wide range of temperatures. Once added to the reaction mixture, the spin trap starts to capture active radicals forming relatively inactive radical species, i.e. spin adducts, which have characteristic ESR-spectra. It is important to note in this context that spin traps do not react with stable or relatively stable radicals.14 These spin adducts are stable enough to be observed by ESR-spectroscopy; by integration of each of these signals, one can measure the concentrations of each species and thereby study the kinetics of the process. At the same time, the spin traps themselves act as a constant “radical vacuum cleaner”, mopping up the released radicals and preventing side reactions, such as termination processes or re-addition of radicals to the RAFT agent. This implies that the reaction scheme can be greatly simplified. Using the model compounds employed herein – rather than a full polymerizing system – the rate and equilibrium constants can thus be measured more directly, with significantly reduced dependence on model-based assumptions than the previous ESR studies.4,12
A key challenge to applying this approach to dithioester RAFT agents is the need to avoid the problem of photo-induced decomposition. To this end, in contrast to experiments described before,12 all of the experiments were carried out at room temperature using a spin trap, 2-methyl-2-nitrosopropane (MNP) that functions simultaneously as a visible-light photoinitiator.
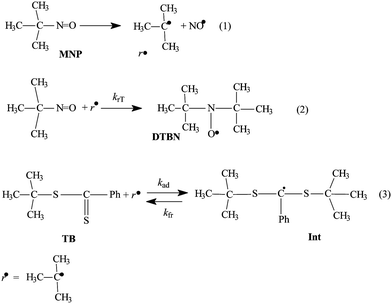
When irradiated by visible light, MNP decomposes and forms an active tert-butyl radical (Scheme 1, reaction 1); in solvents like benzene the tert-butyl radical rapidly interacts with another MNP species and forms the stable nitroxide radical di-tert-butylnitroxide (DTBN), which has its own specific ESR-spectrum (reaction 2). When a RAFT agent such as tert-butyl dithiobenzoate (TB) is added to the system, the tert-butyl radical can interact with it (reaction 3). It is important to note that the presence of RAFT agent does not influence the MNP decomposition under visible light; the use of visible light (instead of UV) also avoids the problems of RAFT agent absorbance and – importantly – its decomposition.
The observed ESR-spectrum for the system TB–MNP–benzene at 20 °C is given in Fig. 1, and is evidently a result of the superposition of the signals attributed to the spin adduct DTBN (triplet with AN = 15.1 G) and multiplet (g = 2.0041 G, AδH = 0.42 G, AoH = 3.65 G, AmH = 1.34 G, ApH = 3.99 G) corresponding to the intermediate radical (Int) formed in reaction 3. We have observed analogous spectra before upon irradiation of MNP in benzene solution and upon heating TB with AIBN, benzene and styrene;15 examples are provided in Fig. S1 and S2 of the ESI.† As both of the signals are very intense, we can use them to evaluate the concentrations of the respective radicals: for DTBN the end component of the spectrum was used for integration; for Int the third component was used.14b
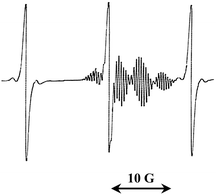 | ||
| Fig. 1 An ESR-spectrum observed upon irradiation by visible light (through red light filter RL-15 with λ > 650 nm) of the TB–MNP–benzene system at 20 °C. | ||
During irradiation, the DTBN and the Int concentrations both increase as a result of the trapping of tert-butyl radicals by MNP and TB, respectively. After the irradiation is switched off the DTBN concentration increases, while the Int concentration slowly decreases (Fig. 2). This is because the intermediate radical has a finite lifetime and it decomposes releasing tert-butyl radicals (reverse of reaction 3), which are subsequently trapped by MNP forming DTBN (reaction 2).
![Kinetic curves of accumulation and consumption of intermediate radical Int (1) and DTBN (2) in the system TB–MNP–benzene after switch-off of MNP photolysis: [TB] × 102 = 1 (a) and 9 (b) and [MNP] = 10−2 mol L−1 at 20 °C. Curves for other concentrations and full experimental details are provided in the ESI.](/image/article/2010/PY/c0py00245c/c0py00245c-f2.gif) | ||
| Fig. 2 Kinetic curves of accumulation and consumption of intermediate radical Int (1) and DTBN (2) in the system TB–MNP–benzene after switch-off of MNP photolysis: [TB] × 102 = 1 (a) and 9 (b) and [MNP] = 10−2 mol L−1 at 20 °C. Curves for other concentrations and full experimental details are provided in the ESI†. | ||
If the irradiation time is noticeably less than the intermediate lifetime (e.g., in the present work the irradiation time is 5 s whilst the intermediate decays over several hundred seconds), we can separately consider the processes of intermediate accumulation and consumption; for DTBN all side reactions (Scheme 2) may be also excluded due to short period of irradiation. Thus, the ratio of the DTBN to Int formed during irradiation provides a measure of the relative rates of tert-butyl radical addition to MNP versus to TB: that is, [DTBN]0/[Int]0 = krT[MNP]0/kad[TB]0. In this equation, [DTBN]0 and [Int]0 are obtained by the extrapolation of the kinetic curves up to zero time, [MNP]0 and [TB]0 are preset, and krT = 3.3 × 106 L mol−1 s−1,16 and hence kad can be obtained. Over the range of TB concentrations 10−2 – 10−1 mol L−1 and at [MNP] = 10−2 mol L−1 the average value of rate coefficient of tert-butyl radical addition to TB was found to be equal to (5 ± 1)×106 L mol−1 s−1; a collation of kad values obtained under various TB concentrations is provided in Table S1 of the ESI.† These results are in good qualitative agreement with both experimental4 and theoretical6d values reported in the literature for the addition of oligomeric and polymeric radicals to various RAFT agents.
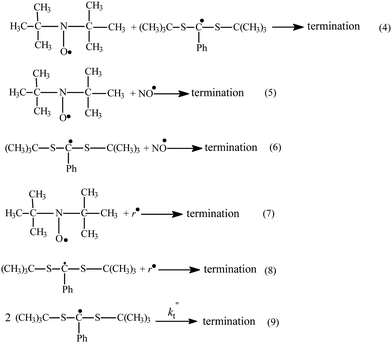 | ||
| Scheme 2 The reactions taking place after switch-off irradiation of the MNP–TB–benzene system at 20 °C. | ||
Provided the only pathway affecting the concentration of the Int after switch-off is the fragmentation reaction (i.e. reverse of reaction 3), its rate coefficient kfr can be measured directly from the slope of the kinetic curves of intermediate consumption after switch-off, when plotted in semi-logarithmic form (Fig. 3): kfr = (5 ± 1)×10−3 s−1. However, for this to be a valid direct measure of this rate coefficient, it is important to consider the likelihood and effect of any additional side reactions that might affect the Int concentration during switch off. These possible reactions include re-addition of the tert-butyl radical to the RAFT (reaction 3), and various possible termination reactions (see Scheme 2, reactions 4, 6, 8 and 9).
![Semi-logarithmic plot of the kinetic curves 1 presented in Fig. 2a and 2b, [TB] × 102 = 1 mol L−1 (1) and 9 mol L−1 (2).](/image/article/2010/PY/c0py00245c/c0py00245c-f3.gif) | ||
| Fig. 3 Semi-logarithmic plot of the kinetic curves 1 presented in Fig. 2a and 2b, [TB] × 102 = 1 mol L−1 (1) and 9 mol L−1 (2). | ||
The addition reaction (3) would contribute to an increase in the intermediate concentration and cause the decay to occur over a longer time period, leading us to underestimate the decay rate. However, the experimental design of our current study largely excludes the re-addition of tert-butyl radicals to TB, as the released radicals are immediately trapped by the high spin trap concentration. This is one of the key differences between the current case and the earlier laser flash photolysis experiments of RAFT polymerization; in the latter experiment there is no spin trap present and thus the released radical can undergo re-addition, along with other reactions such as propagation, termination, transfer, etc. However, for the sake of rigor, we can take the addition reaction into account explicitly using the correction factor p = Rad/(RrT + Rad) = kad[TB]/(krT[MNP] + kad[TB]), where RrT and Rad are the rates of tert-butyl radical addition to MNP and TB, correspondingly. For [TB] = [MNP] = 10−2 mol L−1 the p value is 0.6; i.e. the real kfr is slightly higher: kfr = kfrexp/p = (8 ± 2)×10−3 s−1.
The various termination reactions are more difficult to rule out completely but it is important to note that if any of these do occur, they would contribute to a decrease in the intermediate concentration and cause the decay to occur over a shorter time period than in their absence. In other words, in this experimental set-up, if Int termination processes are important, our fragmentation rate coefficient provides an upperbound to the true value. In fact the linear dependence of Fig. 3 indicates that at the chosen conditions all side reactions (4, 6, 8, 9) involving intermediate radical can be largely excluded, and are unlikely to be affecting the results. However, there is evidence that termination processes are occurring to a small extent, and this is now examined in detail.
After switching off the irradiation, the intermediate radical very slowly vanishes over a 10–15 min period depending on the MNP and TB concentrations; simultaneously the DTBN concentration increases (Fig. 2). This latter effect is due to the production of tert-butyl radicals during intermediate fragmentation. Thus, MNP should quantitatively register the intermediate fragmentation events. In this case the number of additional DTBN adducts formed should be equal to the number of intermediate radicals consumed; indeed, this is observed when equal amounts of MNP and TB are present (Fig. 2a). However, as the ratio of TB to MNP increases, one observes that there is a greater loss of intermediate radicals than the corresponding increase in DTBN concentration (Fig. 2b). This could either be as a result of the additional consumption of Int by termination reactions such as 6, 8 or 9 in Scheme 2, or the consumption of the DTBN itself via by termination reactions 5 and 7. The remaining process in Scheme 2, termination reaction 4, consumes both Int and DTBN and does not affect their concentration ratio.
The reactions of DTBN and Int with NO radicals (reactions 5 and 6) can be ruled out as they require NO to be produced in significant quantities through the decomposition of MNP; this will only occur over a long duration of irradiation and at high MNP concentrations. The reaction of DTBN with tert-butyl radicals (reaction 7) is well known, and when it plays a visible role the DTBN kinetic curve reaches its saturation limit. However, we have designed our experimental conditions so that this reaction can also be neglected due to the low concentration of tert-butyl radicals compared with MNP and TB. This was confirmed by showing in an independent experiment that the DTBN concentration increased linearly with growth of irradiation time, and hence reaction 7 was not consuming DTBN. This leaves the termination of the Int via coupling either with tert-butyl radical (reaction 8) or with itself (reaction 9). Whilst both reactions are plausible from a chemical perspective, under the present reaction conditions reaction 8 can also be excluded. Even if its rate coefficient is assumed to be of a similar magnitude to the rate coefficient of tert-butyl radical reaction with DTBN, TB and MNP (106–107 L mol−1 s−1); as the intermediate concentration is 3–4 orders of magnitude lower than that of MNP and TB, reaction 4 cannot compete with reactions of tert-butyl radical with TB and MNP under these conditions.
Thus, the only plausible pathway for the consumption of intermediate radicals in these experiments is their self-termination (reaction 9). Since this reaction becomes more likely as the Int concentration increases, we examine the system with highest concentration of TB (Fig. 2b). It is obvious that the termination rate kt′′ can be calculated as the difference between the rate of intermediate radical consumption and the rate of DTBN accumulation. This leads to eqn (10):
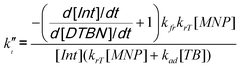 | (10) |
From the measured concentrations (Fig. 2b) and the measured rate coefficients, this is equal to (6.5 ± 3.0) × 102 L mol−1 s−1.
Finally, having measured the addition and fragmentation rate coefficients, and verified that other reactions are not substantially affecting the results, we can obtain the first directly measured experimental equilibrium constant K = kad/kfr for reaction (3) as (6 ± 4)×108 L mol−1. This can then be compared with quantum-chemical calculations on the same system under the same conditions (i.e. at 20 °C in benzene solution). To this end, we used the same methodology as in our recent study of S–S′-bis(methyl-2-propionate)-trithiocarbonate mediated polymerization of methyl acrylate;13 full computational details are provided in the ESI.† The equilibrium constant we obtain for the present system is 4.5 ×108 L mol−1, which is in excellent agreement with the experimental results. This result therefore further reinforces the accuracy and applicability of our quantum-chemical methodology for model RAFT reactions.
Conclusions
In conclusion, we have used an ESR-based spin trapping technique to provide the first direct experimental measurements for the rate coefficients of the addition and fragmentation reactions of tert-butyl dithiobenzoate. The results indicate that the fragmentation processes of dithiobenzoate derived intermediate RAFT radicals can be relatively slow, in agreement with the original predictions of the so-called slow fragmentation model.6,9 The equilibrium constant of (6 ± 4) × 108 L mol−1 at 20 °C in benzene is in excellent agreement with the corresponding quantum-chemical calculations for the same reaction 4.5 × 108 L mol−1, mutually verifying the accuracy of the experimental and theoretical results. Our results also confirm that intermediate self-termination can occur, albeit at a relatively low reaction rate (kt′′= (6.5 ± 3.0) × 102 L mol−1 s−1), at least for the low molecular weight model compound studied.Acknowledgements
MLC gratefully acknowledges financial support from the Australian Research Council under their Centres of Excellence program and generous allocations of supercomputing time on the National Facility of the National Computational Infrastructure. EC gratefully acknowledges financial support from the Russian Foundation for Basic Research (project No 08-03-00269).References
- G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2005, 58, 379 CrossRef CAS.
- For a review see: C. Barner-Kowollik, M. Buback, B. Charleux, M. L. Coote, M. Drache, T. Fukuda, A. Goto, B. Klumperman, A. B. Lowe, J. B. McLeary, G. Moad, M. J. Monteiro, R. D. Sanderson, M. P. Tonge and P. Vana, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 5809 Search PubMed.
- For an updated account, see: B. Klumperman, E. T. A. van Dungen, J. P. A. Heuts and M. J. Monteiro, Macromol. Rapid Commun., 2010 DOI:10.1002/marc.200900907.
- See for example: Y. Kwak, A. Goto, Y. Tsuji, Y. Murata, K. Komatsu and T. Fukuda, Macromolecules, 2002, 35, 3026 Search PubMed.
- See for example: (a) S. L. Brown, D. Konkolewicz, A. Gray-Weale, W. B. Motherwell and S. Perrier, Aust. J. Chem., 2009, 62, 1533 CrossRef CAS; (b) A. Feldermann, A. Ah. Toy, T. P. Davis, M. H. Stenzel and C. Barner-Kowollik, Polymer, 2005, 46, 8448 CrossRef CAS; (c) A. Ah. Toy, P. Vana, T. P. Davis and C. Barner-Kowollik, Macromolecules, 2004, 37, 744 CrossRef.
- (a) M. L. Coote and L. Radom, J. Am. Chem. Soc., 2003, 125, 1490 CrossRef CAS; (b) M. L. Coote, Macromolecules, 2004, 37, 5023 CrossRef CAS; (c) A. Feldermann, M. L. Coote, M. H. Stenzel, T. P. Davis and C. Barner-Kowollik, J. Am. Chem. Soc., 2004, 126, 15915 CrossRef CAS; (d) M. L. Coote, J. Phys. Chem. A, 2005, 109, 1230 CrossRef CAS; (e) M. L. Coote, E. H. Krenske and E. I. Izgorodina, Macromol. Rapid Commun., 2006, 27, 473 CrossRef CAS; (f) C. Barner-Kowollik, M. L. Coote, T. P. Davis, L. Radom and P. Vana, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 2828–2832 CrossRef CAS.
- C. Barner-Kowollik, P. Vana, J. F. Quinn and T. P. Davis, J. Polym. Sci., Part A: Polym. Chem., 2002, 40, 1058 CrossRef CAS.
- (a) A. Ah. Toy, H. Chaffey-Millar, T. P. Davis, M. H. Stenzel, E. I. Izgorodina, M. L. Coote and C. Barner-Kowollik, Chem. Commun., 2006, 835 RSC; (b) F. Günzler, T. Junkers and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 1864; (c) T. Junkers, M. H. Stenzel, T. P. Davis and C. Barner-Kowollik, Macromol. Rapid Commun., 2007, 28, 746 CrossRef CAS.
- C. Barner-Kowollik, J. F. Quinn, J. R. Morsley and T. P. Davis, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 1353 CrossRef CAS.
- M. Buback, O. Janssen, R. Oswald, S. Schmatz and P. Vana, Macromol. Symp., 2007, 248, 158 CrossRef CAS.
- D. Konkolewicz, B. S. Hawkett, A. Gray-Weale and S. B. Perrier, Macromolecules, 2008, 41, 6400 CrossRef CAS.
- M. Buback, P. Hesse, T. Junkers and P. Vana, Macromol. Rapid Commun., 2006, 27, 182 CrossRef CAS.
- C. Y. Lin and M. L. Coote, Aust. J. Chem., 2009, 62, 1479 CrossRef CAS.
- (a) J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance, Elementary Theory and Practical Applications, 2nd edn, 2007Wiley-Interscience, Hoboken, New Jersey Search PubMed; (b) V. E. Zubarev, Spin Trapping Technique, MSU, Moscow, 1984 Search PubMed.
- (a) E. Chernikova, A. Morozov, E. Leonova, E. Garina, V. Golubev, C. Bui and B. Charleux, Macromolecules, 2004, 37, 6329 CrossRef CAS; (b) V. B. Golubev, E. V. Chernikova, E. A. Leonova and A. V. Morozov, Polymer Sci., Ser. A, 2005, 47, 678 Search PubMed.
- T. Doba, T. Ichikawa and H. Yoshida, Bull. Chem. Soc. Jpn., 1977, 50, 3158 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional kinetic and computational data, and full descriptions of the experimental and theoretical procedures. See DOI: 10.1039/c0py00245c |
| This journal is © The Royal Society of Chemistry 2010 |