The norbornene mystery revealed†‡
Stephan N.
Steinmann
a,
Pierre
Vogel
a,
Yirong
Mo
b and
Clémence
Corminboeuf
*a
aInstitute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne EPFL SB ISIC, Lausanne, Switzerland. E-mail: clemence.corminboeuf@epfl.ch; Fax: (+)41 (0)21 693 97 00
bDepartment of Chemistry, Western Michigan University, Kalamazoo, USA
First published on 24th June 2010
Abstract
The long-standing mystery surrounding the peculiar electronic structure of norbornene and its derivatives is revealed by the direct comparisons of their properties with those of reference analogues with localized double bonds (i.e. Lewis structures). Our block-localized wavefunction analysis coupled with the computations of NMR parameters evidently supports the manifestation of a density redistribution toward an incipient retro-Diels–Alder reaction.
The electronic distribution of norbornene (1b, Fig. 1) derivatives results in exceptional characteristics, which have both puzzled and intrigued theoreticians and experimentalists for decades.1–17 In addition to the non-planarity of the double bond resulting in an unusually high exo-reactivity (the Huisgen's X-factor),4–6,9 other anomalies of the electronic structures are revealed by the nuclear magnetic resonance spectra18–20 as exemplified by the downfield chemical shift of the bridging methylene6,20 and extra large 1J(C–C) couplings.15 Several explanations, e.g.ref. 14 and herein, for these ‘norbornene effects’ have been postulated in the literature, generally based on hyperconjugative interactions and/or torsional strain. However, none of these have proven unequivocally satisfactory, lacking consistent phenomenological explanations and evidence. The investigation of geometries, electron densities and NMR properties of bicyclic skeletons free of π-electron delocalization therefore appears as an ideal strategy to determine the impact of hyperconjugation. We herein propose a combined methodology that not only identifies the origin of the norbornene peculiarity fully, but more generally allows for straightforwardly interpreting the origin of exceptional molecular properties and features.
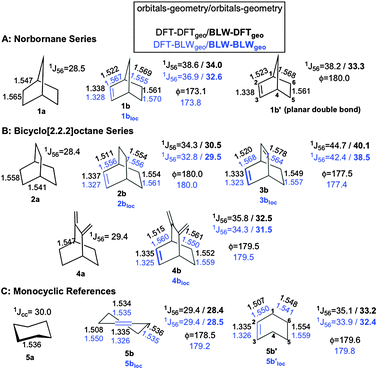 | ||
| Fig. 1 B3LYP/6-311+G** bond distances (in Å) are given for 1b–5b and for their references 1a–5a. Bond distances referring to the BLW-optimized geometries are indicated by ‘loc’ (i.e., 1blocloc–5blocloc) in blue. The PBE/IGLO-III 1J(CC) (in Hertz) are computed for both the standard and ‘loc’ geometries. Values in bold indicate that BLW-orbitals are used to compute the J-coupling constants. ϕ defines the planarity of the double bonds. For convenience, the skeleton numbering refers to norbornene. | ||
The deactivation of π-electron delocalization is formally achieved by constructing a resonance (i.e. Lewis) structure that can be expressed by a block-localized wavefunction (BLW).21–23 The latter distributes electrons in separate subgroups and confines two π-electrons to only two related carbon atoms. The interaction between the occupied/virtual π MOs and the virtual/occupied MOs of other subgroups is quenched, hence so is the delocalization of the π-electrons. Our recently introduced BLW-IGLO approach24 combines the block-localized wavefunction (BLW)21–23 with the IGLO methodology25 and enables the direct assessment of π-electron delocalization effects on the chemical shift of (hyper)conjugated systems. We herein broaden the methodological scope by enabling the use of the BLW formalism in conjunction with the computation of both NMR chemical shifts and J-coupling constants. More specific details on the use of the BLW-orbitals to compute NMR parameters and on the method accuracy are given in the ESI.‡
The above methodology is now used to directly assess the effects of electron delocalization on geometrical parameters, electron density, chemical shifts and J-coupling constants of a series of bicyclic systems illustrated in Fig. 1. The ultimate goal is to fully characterize the elusive nature of the electronic distribution within these molecules responsible for their peculiar properties.
Note that the localization effects are successively analyzed in terms of geometry and density criteria. In other words, one first compares the geometrical parameters optimized with density functional theory (DFT) and BLW prior to computing the molecular properties using either the unconstrained DFT (canonical) or constrained (BLW) density for both the DFT and the BLW-optimized geometries.
Labeling in Fig. 1 distinguishes standard DFT structures from localized geometries (BLW-optimized) denoted ‘loc’. Several relevant features characterize the geometrical parameters of the bicyclic systems after the localization of the π-bond. The deviation from planarity for the double bond in 1blocloc–3blocloc is unaffected by the localization of the π-electrons. This persistence tends to disprove the hyperconjugative model in favor of torsional repulsion but more discussion relative to the double bond geometry will be provided shortly. 1blocloc–3blocloc also possess shorter double and significantly longer single C–C bonds as compared to the canonical structures. Upon localization, the double bond undergoes a consistent 0.01 Å shortening, whereas the allylic bond elongates by up to 0.05 Å within the molecular series. These distortions are, however, not unique to the bicyclic systems as they take place in all classical hyperconjugated molecules (e.g.propene (0.04 Å) and monocycles 5b and 5b′). In contrast, the elongation/shortening of the C5–C6/C4–C5 bonds does not occur in the half chair conformation of cyclohexene (5b). These tendencies are, at first glance, compatible with the geometrical manifestation of a partial retro-Diels–Alder (rDA) reaction (Fig. 2), first advocated by Vogel et al.15 The constrained BLW geometries represent ideal references, with double and single C–C bond distances manifesting no distortion toward a rDA reaction coordinate. This provides an enhanced picture in comparison to the conclusions drawn from X-ray crystal structures.16,17
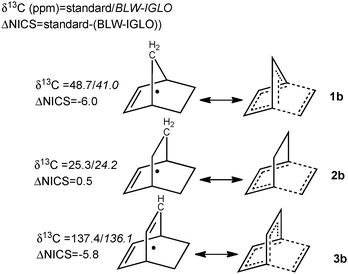 | ||
| Fig. 2 Illustration of the manifestation of partial retro-Diels–Alder reaction for 1b–3b. δ(13C) and Nucleus-Independent Chemical Shifts (NICS) at the locations denoted with black dots are computed at the IGLO-PW91/IGLO-III level for the standard and the BLW-orbitals (in italic). More details are given in the ESI.‡ | ||
Vogel's original proposal15 was intended to account for the most intriguing yet unresolved phenomenon: a 10 Hz increase of the 1J(C5C6) coupling constant of the saturated trinorbornane-like system, upon introduction of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond at the position 2,3 (1a and 1b in Fig. 1), while no such variation is observed in monocyclic systems like 5b. The much larger coupling differences observed for the higher homologues bicyclo[2.2.2]octadiene (3b) (16 Hz increase compared to 2a) contrasting with the smaller effects (6 Hz increase) detected in bicyclo[2.2.2]octene (2b) also are unproven. Unexpectedly, the computation of the J-couplings at the distorted geometries of 1blocloc–3blocloc lowers 1J(C5C6) by about 2.0 Hz only. Thus, the geometrical parameters are unable to fully validate the rDA model and explain the observed NMR effects.
C double bond at the position 2,3 (1a and 1b in Fig. 1), while no such variation is observed in monocyclic systems like 5b. The much larger coupling differences observed for the higher homologues bicyclo[2.2.2]octadiene (3b) (16 Hz increase compared to 2a) contrasting with the smaller effects (6 Hz increase) detected in bicyclo[2.2.2]octene (2b) also are unproven. Unexpectedly, the computation of the J-couplings at the distorted geometries of 1blocloc–3blocloc lowers 1J(C5C6) by about 2.0 Hz only. Thus, the geometrical parameters are unable to fully validate the rDA model and explain the observed NMR effects.
A more sensitive question is: how does the density (rather than the geometry) rearrange upon localization of the double bond? While such a question is impossible to address solely on the basis of experimental data, unambiguous answers are provided for the first time in Fig. 3. Fig. 3 shows the electron density difference (EDD) maps between the standard and BLW-constrained states of three illustrative systems. The real electronic distributions of 1b–3b clearly manifest contributions from the partial retro-Diels–Alder resonance forms, showing higher density (positive difference = green) in the supposed diene and ene regions. In contrast, the BLW density (BLW-1b–3b) that is constrained to the cycloadduct-type form (left in Fig. 2) exhibits a higher density in the regions of the two formed C–C single bonds (red = negative difference). These contrasting features are a direct indication of partial retro-Diels–Alder character of the unsaturated bicyclic system. This electronic evidence is further supported by the computed 1J(C5C6) values, which change noticeably upon localization of the density. Blocking the double bond in bicyclo[2.2.2]octene lowers the coupling value by 3.8 Hz from 34.3 to 30.5 Hz (BLW-2b in Fig. 1). If using the localized geometry (BLW-2blocloc), the coupling constant comes even closer to the reference value of the saturated analogue (2a) having a pure single C5(sp3)–C6(sp3)-bond (29.5 vs. 28.4 Hz). The 6 Hz difference between 1J(C5C6) of 2b and 2a is evidently the signature of a density redistribution upon an incipient retro-Diels–Alder reaction. The bond distance deformation contributes to the effect but only by a small fraction.
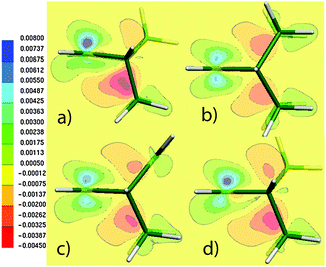 | ||
| Fig. 3 Projection plots of the difference between the PBE/IGLO-III density and the density computed at the same level but using the BLW-orbitals for (a) 1b, (b) 2b, (c) 3b and (d) 1b′. Maps are in the C3C4C5 plane. | ||
Along this line, one can predict that favoring the rDA reaction even more would result in larger density redistribution. The origin of the much larger coupling difference observed between bicyclo[2.2.2]octadiene (3b, 16 Hz), norbornene (1b, 10 Hz), and their saturated analogues bicyclo[2.2.2]octane (2a) and norbornane (1a) can be clarified on this basis. The rDA reaction of 3b tends towards a highly stabilized transition state with 8 delocalized electrons shared between three cyclic arrays of 6 electrons. Two arrays (by symmetry) are characteristic of the pericyclic transition state, which are coupled with a restituted benzene-like structure (Fig. 2). The large 1J(C5C6) enhancement in 3b is thus a manifestation of a more delocalized density as compared to 2b that is confirmed by the NICS-based index26,27 (−5.8 vs. 0.5, see ESI for details‡). Blocking one of the π-bonds in 3b and optimizing the geometry (BLW-3blocloc) disables one of the cyclic arrays and lowers the coupling by 6.2 Hz to 38.5 Hz. The residual delocalization of the remaining array can be attenuated in BLW-4blocloc (31.5 Hz) that mimics the simultaneous blocking of the two π-bonds (technically unfeasible).28 To a lesser extent, a similar pattern of 8 delocalized electrons characterizes norbornene (1b). The cyclopentadiene-type electronic structure in 1b exhibits some borderline aromatic character24,29 due to the hyperconjugative interaction with the methylene group illustrated by the downfield δ(13C) of the bridging carbon (48.7 ppm) as compared to norbornane (δ(13C) = 37.2 ppm). Going from 1b to BLW-1blocloc shifts the δ13C upfield to 41.0 ppm and decreases 1J(C5C6) by 6.2 Hz. Note that imposing a planar double bond in norbornene (1b′) does not produce coupling constants any different than 1b. On the other hand, the planarization of the double bond is shown to symmetrize the density among the exo/endo faces (Fig. 3d). This computational experiment distinguishes (i) the consequence of the non-planarity of the double-bond: a short-range rearrangement of the density affecting the exo-reactivity and (ii) the extent of rDA character: a long-range manifestation detectable in the NMR parameters. Additional examples presented in Fig. 4 corroborate an electronic manifestation of a rDA reaction. The effects in the norbornene skeleton can be tuned by the introduction of a greater/lesser π-donating group24,29 as demonstrated by the larger and smaller values in respectively 6, 7 and 8 or by the introduction of an attenuator like the benzene ring in 9.15 Although less dramatic, the BLW-effects on other coupling constants (e.g.1J(C1C6) and 1J(C1C2) in the supporting information‡) are also in line with the conclusions given herein.
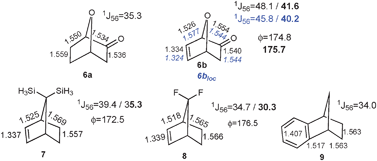 | ||
| Fig. 4 B3LYP/6-311+G** bond distances for 6–9 (in Å). BLW-optimized geometrical parameters are given in blue for 6blocloc. The 1J(CC) (in Hertz) are computed at the PBE/IGLO-III level. Values in bold indicate the use of BLW-orbitals in the J-coupling computation. ϕ defines the planarity of the double bonds. For convenience, the skeleton numbering is the same as in Fig. 1. | ||
In summary, the present computational scheme solves the long-standing mystery surrounding the electronic structure of norbornene and its derivatives. The comparisons of the electronic and magnetic properties of a series of bicyclic molecules with those of their reference analogues with localized double bonds unequivocally support the retro-Diels–Alder picture. Our results also demonstrate that these peculiar electronic effects correlate with the increase of delocalization in the rDA transition state. To some extent, the bond distance distortions also alter the long-range redistribution of the density. In contrast, the degree of pyramidalization of the double bond has no effect on the properties. The BLW analysis coupled with the computations of NMR parameters is highly encouraged to solve problems and place the hypothesis on firmer ground.
We thank the Sandoz family foundation, the Swiss NSF Grant 200021_121577/1, and EPFL for financial support.
Notes and references
- K. Alder, G. Stein and H. Finzenhagen, Justus Liebigs Ann. Chem., 1931, 485, 211–222 CrossRef CAS.
- P. v. R. Schleyer, J. Am. Chem. Soc., 1958, 80, 1700–1704 CrossRef CAS.
- P. v. R. Schleyer, J. Am. Chem. Soc., 1967, 89, 699–701 CrossRef CAS.
- P. v. R. Schleyer, J. Am. Chem. Soc., 1967, 89, 701–703 CrossRef CAS.
- R. C. Fahey, in Topics in Stereochemistry, ed. E. L. E. Norman and L. Allinger, John Wiley & Sons, New York, 1968, pp. 237–342 Search PubMed.
- J. D. Roberts, J. B. Grutzner, M. Jautelat, J. B. Dence and R. A. Smith, J. Am. Chem. Soc., 1970, 92, 7107–7120 CrossRef.
- R. Huisgen, P. H. J. Ooms, M. Mingin and N. L. Allinger, J. Am. Chem. Soc., 1980, 102, 3951–3953 CrossRef CAS.
- A. A. Pinkerton, D. Schwarzenbach, J. H. A. Stibbard, P. A. Carrupt and P. Vogel, J. Am. Chem. Soc., 1981, 103, 2095–2096 CrossRef CAS.
- R. Huisgen, Pure Appl. Chem., 1981, 53, 171–187 CAS.
- K. N. Houk, N. G. Rondan, F. K. Brown, W. L. Jorgensen, J. D. Madura and D. C. Spellmeyer, J. Am. Chem. Soc., 1983, 105, 5980–5988 CrossRef CAS.
- F. K. Brown and K. N. Houk, J. Am. Chem. Soc., 1985, 107, 1971–1978 CrossRef CAS.
- O. Ermer, P. Bell and S. A. Mason, Angew. Chem., Int. Ed. Engl., 1989, 28, 1239–1241 CrossRef.
- A. Rastelli, M. Cocchi, E. Schiatti, R. Gandolfi and M. Burdisso, J. Chem. Soc., Faraday Trans., 1990, 86, 783–787 RSC.
- M. C. Holthausen and W. Koch, J. Phys. Chem., 1993, 97, 10021–10027 CrossRef CAS.
- G. R. Jones, S. Caldarelli and P. Vogel, Helv. Chim. Acta, 1997, 80, 59–64 CrossRef CAS.
- B. R. Pool and J. M. White, Org. Lett., 2000, 2, 3505–3507 CrossRef CAS.
- D. Birney, T. K. Lim, J. H. P. Koh, B. R. Pool and J. M. White, J. Am. Chem. Soc., 2002, 124, 5091–5099 CrossRef CAS.
- R. R. Fraser, Can. J. Chem., 1962, 40, 78 CrossRef CAS.
- P. Laszlo and P. v. R. Schleyer, J. Am. Chem. Soc., 1964, 86, 1171–1179 CrossRef CAS.
- M. Hesse, H. Meier and B. Zeeh, Spektroskopische Methoden in der organischen Chemie, Georg Thieme Verlag, New York, 2002 Search PubMed.
- Y. Mo and S. D. Peyerimhoff, J. Chem. Phys., 1998, 109, 1687–1697 CrossRef CAS.
- Y. Mo, J. Gao and S. D. Peyerimhoff, J. Chem. Phys., 2000, 112, 5530–5538 CrossRef CAS.
- Y. Mo, J. Chem. Phys., 2003, 119, 1300–1306 CrossRef CAS.
- S. N. Steinmann, D. F. Jana, J. I.-C. Wu, P. v. R. Schleyer, Y. Mo and C. Corminboeuf, Angew. Chem., Int. Ed., 2009, 48, 9828–9833 CrossRef CAS.
- W. Kutzelnigg, Isr. J. Chem., 1980, 19, 193 CAS.
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. J. Jiao and N. J. R. V. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS.
- Z. F. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS.
- The current version of the BLW module only allows the simultaneous blocking of orthogonal or parallel bonds only.
- L. Nyulaszi and P. v. R. Schleyer, J. Am. Chem. Soc., 1999, 121, 6872–6875 CrossRef CAS.
Footnotes |
| † This article is part of the ‘Emerging Investigators’ themed issue for ChemComm and is dedicated to Paul von Ragué Schleyer on the occasion of his 80th birthday. |
| ‡ Electronic supplementary information (ESI) available: Methods section, Cartesian coordinates and coupling constants of molecules discussed. See DOI: 10.1039/c0cc00601g |
| This journal is © The Royal Society of Chemistry 2011 |
