On multiferroicity of TTF-CA molecular crystal

Abstract

Magnetic properties of the TTF-CA molecular crystal below the neutral to ionic transition temperature are studied using the embedded cluster approach in combination with density functional theory. The calculated values of the Heisenberg exchange integral between the neighboring TTF and CA molecules stacked along the crystallographic axis a suggest that the ionic phase of the TTF-CA can be described as an alternating antiferromagnetic spin-1/2 Heisenberg chain with the exchange integral J = 1124 cm⁻¹ and the alternation parameter δ = 0.46. Although the combination of ferroelectricity of the ionic phase with the antiferromagnetic ordering renders TTF-CA multiferroic (as predicted theoretically in G. Giovannetti et al., Phys. Rev. Lett., 2009, 103, 266401), the large value of the alternation parameter should result in a nonmagnetic ground state of this phase. The dependence of the magnetic coupling parameters on the crystal structure is studied and the implications for experimental observation of magnetic properties of TTF-CA are discussed.

---

1. Introduction

Mixed stack organic charge-transfer complexes¹ have been the subject of intense investigation over the last decades.^2–13 Among other compounds of this type the tetrathiafulvalene (TTF)-p-chloranil (CA) molecular crystal attracts considerable attention for its ability to undergo a neutral to ionic (NI) phase transition under the influence of external stimuli, such as cooling under the atmospheric pressure,³ elevated external pressure,^2,7,8 and photoirradiation.^10,14 At ambient temperature and pressure, TTF-CA is in the neutral phase in which the TTF and CA molecules are stacked alternately at an equal distance along the stacking axis. Below the NI transition temperature (ca. 84 K),³ there occurs a partial electron transfer between the TTF and CA molecules and the symmetry along the stacking axis is broken due to the formation of weakly bound TTF-CA dimers.⁹ As a result of broken symmetry and electron transfer the ionic phase acquires ferroelectric properties.

Recently, a coexistence of the ferroelectricity and antiferromagnetism in TTF-CA was predicted based on the periodic electronic structure calculations.¹² Indeed, the electron transfer should result in the occurrence of unpaired electrons on the TTF⁺ and CA⁻ molecular ions which may be sufficiently strongly coupled in order to lead to a long range magnetic order. Hence, this theoretical prediction renders the TTF-CA crystal a plausible candidacy in the search for organic multiferroics. However, despite that TTF-CA was at the focus of intense experimental investigation for several decades, there were no reports on its antiferromagnetism. To the contrary, the experimental observation of a nonmagnetic ground state was reported for the ionic phase of a related compound, TTF-BA (BA = bromanil).¹⁵ It is therefore desirable to investigate the magnetic properties of the TTF-CA crystal in more detail.

It is the primary purpose of the present work to investigate the magnetic coupling between the adjacent TTF⁺ and CA⁻ molecular ions in the low-temperature phase of the TTF-CA crystal. Specifically, the focus will be on the alternation of the magnetic coupling parameters along the stacking axis. Indeed, whereas an ideal uniform spin-1/2 Heisenberg chain features a gapless excitation spectrum,^16,17 a finite excitation gap opens up in the spectrum of an alternating Heisenberg chain and, if sufficiently wide, it should lead to a nonmagnetic ground state.^17,18 The dependence of the magnetic coupling parameters on the crystal structure and on the magnitude of the alternation along the stacking axis will be studied and the implications for experimental observation of magnetic properties of TTF-CA will be discussed.

2. Details of calculations

The crystal structure of the ionic phase of the TTF-CA molecular crystal at T = 40 K was taken from Le Cointe et al.⁹ The symmetry of the unit cell is monoclinic with the space group P1n1 and each unit cell contains two formula units which are stacked alternately along the stacking direction a. The dimensions of the unit cell are a = 7.19 Å, b = 7.54 Å, c = 14.44 Å, and β = 98.6° (see Fig. 1).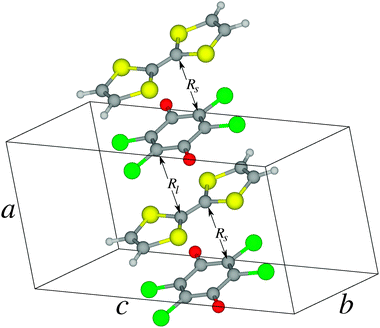

Fig. 1 Crystal structure of the TTF-CA crystal at 40 K.

The focus of this work is on the study of magnetic coupling parameters between the nearest neighbor structural units of the TTF-CA crystal. Therefore, following Illas,¹⁹ the embedded cluster approach²⁰ is adopted. The selected cluster models (see section 3) are embedded into the Madelung field of the crystal represented by the electric field of an array of point charges located at the crystallographic atomic positions. Thus, each TTF-CA cluster is embedded into an array of 263 248 point charges. The magnitudes of the charges are obtained iteratively from a series of calculations in which the environmental charges were assigned the same values as the Mulliken atomic charges of the embedded cluster. The convergence of iterations was reached when the absolute difference between the charges obtained in the successive iterations was less than 10⁻⁴ē.

Calculations of the closed-shell and antiferromagnetically coupled species were carried out using the spin-restricted ensemble-referenced Kohn–Sham (REKS) method²¹ in combination with the BH&HLYP density functional.^22,23 In the REKS method, the strong non-dynamic electron correlation occurring in molecular systems with the antiferromagnetically coupled spin-1/2 centers is modeled by the fractional occupation numbers of the frontier Kohn–Sham orbitals.²⁴ The REKS method provides an accurate account of the static electron correlation effects as was documented in our previous works.^24–28 Molecular models with the high-spin open electronic shells (triplet spin states) were calculated using the spin-restricted open-shell Kohn–Sham (ROKS) method.^29–32 The values of the Heisenberg exchange integrals (see eqn (1)) are evaluated¹⁹ as the energy difference between the antiferromagnetically coupled low-spin state and the high-spin open shell electronic state of the species considered in section 3. Previous application of this approach to the calculation of magnetic coupling parameters in transition metal complexes and organic molecules^24–28 demonstrated its high reliability.

The 6-31G* basis set^33,34 is employed on carbon and hydrogen atoms and the 6-31+G* basis set³⁵ on oxygen atoms. The LANL2DZ effective core potential³⁶ combined with the LANL2DZdp basis set^36,37 is employed on sulfur and chlorine atoms.

3. Results and discussion

In the ionic (T = 40 K) phase of the TTF-CA crystal, the molecules are arranged in mixed stacks with alternating TTF and CA molecules.⁹ Distances between the neighboring molecules along the stacking axis a vary as shown in Fig. 1 such that pairs of molecules with shorter (R_s) and longer (R_l) separations are formed. Formation of the dimers results in breaking the symmetry of the high-temperature phase. Due to a (partial) electron transfer from the donor (TTF) to the acceptor (CA) molecules this leads to a non-zero electric polarization of the crystal.⁹ Obviously, transfer of an electron in the TTF-CA pairs should result in the occurrence of an open-shell electronic configuration where the unpaired electrons of the TTF⁺ and CA⁻ molecular ions can be ferromagnetically or antiferromagnetically coupled.¹⁵ Among other factors, the strength of this coupling depends on the overlap between the electronic wave functions of the neighboring ions.¹⁹ Due to the alternating intermolecular distances, the magnitude of the coupling in short and long TTF-CA pairs should alternate along the stacking axis.

To describe the ionic phase, two molecular models are considered in the present work. Clusters representing the short and the long TTF–CA pairs embedded into the Madelung field of the rest of the crystal are calculated separately. Note that, in a cluster of a bigger size, the non-equivalent TTF or CA molecules would be present. This should result in a deviation of the symmetry of the cluster from the crystal symmetry. Therefore clusters of the minimal size are selected in this work. In the calculations on these clusters, three types of electronic states are considered: a closed-shell (CS) state represented by a single Kohn–Sham determinant, an antiferromagnetically (AF) coupled state represented by an ensemble solution of the REKS method with the fractional occupation numbers of the frontier KS orbitals and a ferromagnetically (FM) coupled (triplet) state with two unpaired electrons in the frontier orbitals of the TTF⁺ and CA⁻ ions. In order to investigate the effect of external pressure on the relative stability of these states, the calculations have been carried out for the experimentally measured crystal structure⁹ as well as for a number of additional crystal structures obtained by varying the lattice parameter along the stacking axis a.

The total energies of the TTF-CA dimers in the CS, AF and FM states are reported in Table 1. The energies of the short and long dimers are reported along with the average energy per dimer. Because each unit cell of the TTF-CA crystal contains two different pairs of TTF and CA molecules (see Fig. 1), the latter energy is used as a measure of the relative stability of different states of the ionic phase of TTF-CA. It is expected that, for each TTF-CA cluster, the major part of the interaction with the neighboring molecules is introduced via the Madelung field of the crystal thus reducing the possible non-additivity effects. Fig. 2 shows the average energy per dimer in the CS, AF and FM states as a function of a.

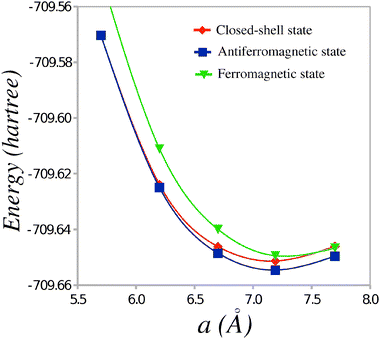Fig. 2 Average energy per dimer as a function of the unit cell parameter a.

Table 1 Total energies (hartrees) of TTF-CA dimers in the closed-shell (CS) state, the antiferromagnetically (AF) coupled state, and the ferromagnetically (FM) coupled state calculated at varying unit cell parameters a. The total energies of the short (R_s) and long (R_L) dimers are reported along with the average energy per dimer

Unit cell	Dimer	E ^CStot	E ^AFtot	E ^FMtot	E ^CSavrg	E ^AFavrg	E ^FMavrg
a This is the experimentally obtained lattice parameter at T = 40 K.^9
a = 5.70 Å	R s = 2.572 Å	−709.542105	−709.536445	−709.506527	−709.570438	−709.570374	−709.548785
	R l = 2.869 Å	−709.598771	−709.604303	−709.591044
a = 6.20 Å	R s = 2.781 Å	−709.606948	−709.600429	−709.580816	−709.623907	−709.624959	−709.611074
	R l = 3.103Å	−709.640867	−709.649488	−709.641332
a = 6.70 Å	R s = 2.991 Å	−709.635731	−709.629200	−709.616896	−709.646186	−709.648531	−709.639976
	R l = 3.338 Å	−709.656641	−709.667861	−709.663057
a = 7.19 Å^a	R s = 3.197 Å	−709.644427	−709.637947	−709.630464	−709.651338	−709.654586	−709.649463
	R l = 3.569 Å	−709.656641	−709.667861	−709.668462
a = 7.70 Å	R s = 3.412 Å	−709.641242	−709.634490	−709.630230	−709.646063	−709.649599	−709.646714
	R l = 3.810 Å	−709.650884	−709.664707	−709.663198

---

Table 1 shows that at the experimental value of the lattice parameter a,⁹ the AF state is the most stable one and the energy difference with respect to the CS state is 0.088 eV per TTF-CA pair. This energy gain is to be compared to the energy difference of 0.080 eV obtained in the broken-symmetry spin-unrestricted DFT calculations by Giovannetti et al.¹² The AF state remains the most stable one at the values of a varying around the experimental value of 7.19 Å. Only at an unrealistically short a = 5.7 Å, the CS state becomes slightly more stable with the energy gain of 0.002 eV. Thus, the AF state should remain the ground state of the ionic phase of TTF-CA crystal at an elevated pressure. A more precise knowledge on the stability of the AF state could be obtained if the crystal structures (including the fractional atomic coordinates) of TTF-CA at high pressure were known.

In the ionic phase, a (partial) electron transfer occurs from the TTF to the CA molecule. The magnitude of the transfer can be evaluated from the absolute values of the Mulliken charges per molecule calculated in the CS, AF and FM states. Fig. 3 shows the dependence of the average absolute charge on the donor or acceptor molecule in the TTF-CA dimers as a function of the unit cell parameter a. At the experimental crystal structure, the magnitude of the electron transfer in the AF and FM states (ca. 0.9 ē) is noticeably greater than in the CS state (ca. 0.5 ē). The former value is in a better agreement with the experimental estimate⁶ of 0.7 ± 0.1 ē for the TTF-CA charge transfer in the ionic phase. Although the magnitude of the electron transfer in the AF state is greater than in the CS state, the electric polarization in the AF state should be smaller. This is due to the alternating dipole moments of the short and long TTF-CA dimers in the ionic phase. Indeed, because the dipole moments of the adjacent dimers point in the opposite directions, there is a substantial compensation of polarization between the dimers. In the AF state, the dipole moments of the short and the long dimers are directed almost entirely along the a crystal axis and possess the values of 15.83 Debye and −18.05 Debye, respectively. In the CS state, the dipole moments of these dimers are 8.10 Debye and −12.10 Debye. Thus, the average dipole moment per TTF-CA dimer in the AF state (−1.11 Debye) is nearly twice as small as in the CS state (−2.00 Debye). A similar two-fold difference between the net polarization in the AF state and in the CS state was found by Giovannetti et al.¹² in the periodic electronic structure calculations.

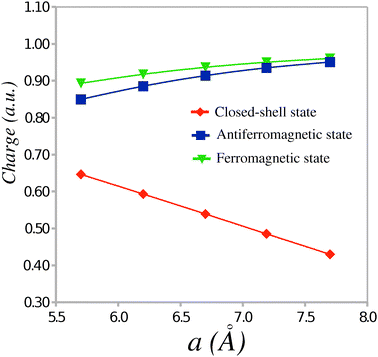Fig. 3 Average absolute charge (ē) per molecule as a function of the unit cell parameter a.

The calculated electronic structure of the ionic phase of TTF-CA crystal suggests the simultaneous presence of the long range electric order (ferroelectricity) as well as the magnetic order. However, the thermodynamic and the magnetic response properties of the AF state are determined by the magnetic excitation spectrum.^16,18 Indeed, the TTF-CA crystal can be viewed as a one-dimensional spin-1/2 AF Heisenberg chain. If the Heisenberg exchange integrals J between the neighboring sites were the same for all nearest neighbor pairs, the excitation spectrum would be gapless.¹⁶ In the case of TTF-CA crystal, the J values in the short and in the long dimers are different which results in an alternating AF Heisenberg chain described by the Hamiltonian 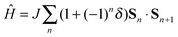(1).

For a non-zero value of the alternation parameter δ, the spin-Peierls (SP) behavior with a non-zero magnetic excitation gap should be observed.^18,38 The magnitude of the excitation gap Δ is proportional to δ^2/3 for small δ and becomes nearly linear for large values of δ.^18,38 Among other consequences, opening the gap may result in the occurrence of anomalies in the specific heat near the temperature of the SP transition.¹⁸

The values of the Heisenberg exchange integral J and the alternation parameter δ (see eqn (1)) were calculated from the energy differences between the AF and FM states of the clusters representing TTF-CA crystal. The calculated J and δ values are plotted in Fig. 4 against the unit cell parameter a. At the experimental crystal structure of the ionic phase (40 K) the Heisenberg exchange integral reaches a value of −1124 cm⁻¹ with the alternation δ = 0.46. According to a recent work of Jiang et al.¹⁸ these values should lead to an excitation gap Δ of the order of 0.5|J| at zero temperature, that is Δ ≈ 560–570 cm⁻¹. As a result of thermal excitations, this gap should close at a critical temperature T_sp that, for δ ≈ 0.5, should lie around T_sp ≈ 0.2|J|/k_B (Boltzmann constant k_B = 0.695030 cm⁻¹ K⁻¹),¹⁸ that is T_sp ≈ 320 K. Because the ionic phase is stable only below ca. 84 K,³ the evaluated SP transition temperature is obviously too high and the ground state should appear nonmagnetic.

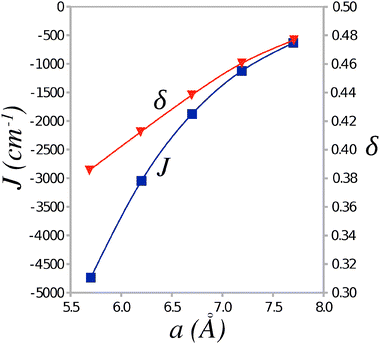Fig. 4 Average value of the Heisenberg exchange integral J and the alternation parameter δ as a function of the unit cell parameter a.

The SP transition temperature can be lowered for smaller value of the Heisenberg exchange integral J and/or smaller values of the alternation parameter δ. Thus stretching the unit cell dimension along the stacking axis a by ca. 0.5 Å results in a lower value of J = −633 cm⁻¹ (see Fig. 4). However, even with this value of J, the transition temperature remains too high, T_sp ≈ 180 K. Apparently, it is the alternation parameter δ (which attains a value δ ≈ 0.5) that prevents lowering of the critical temperature T_sp.

Note that the calculations reported so far are carried out at the geometries obtained from the crystal structure of the ionic phase of TTF-CA measured at 40 K,⁹ well below the NI transition temperature of ca. 84 K.³ In this phase, there is a pronounced alternation of distances between the TTF and CA molecules along the stacking axis (see Table 1). It is noteworthy that the transition between the neutral and ionic phases of TTF-CA occurs gradually, over a range of temperatures,³ and the neutral and ionic phases coexist within this range of temperatures.⁴ Because, in the neutral phase, the TTF and CA molecules are equally spaced,⁹ it may be assumed that, near the temperature of the NI transition, alternation of the TTF-CA distances in the ionic phase is smaller than at T = 40 K.

To investigate the dependence of the parameters of the Heisenberg Hamiltonian (1) on the alternation of TTF–CA distances along the stacking axis a a number of cluster models were generated from the experimental crystal structure by displacing the TTF molecule by Δx/a = 0.01, 0.02, and 0.025 towards the midpoint of the CA⋯CA interval. Calculations of the AF and FM states of these clusters were carried out with the use of the Madelung field obtained for the experimental crystal structure. The calculated values of J and δ are plotted in Fig. 5 against the displacement Δx/a. It is seen that J remains largely constant over this range of displacements, however δ decreases strongly as the geometry along the stacking axis becomes less dimerized at greater values of Δx/a. At a sufficiently symmetric structure (Δx/a ≈ 0.020–0.025), δ drops below 0.1 where the formation of a gapless magnetic excitation spectrum (similar to a uniform AF Heisenberg chain) can be expected.^17,18 One can therefore conjecture that, near the NI transition temperature, a very narrow or vanishing gap Δ is expected that may lead to a possibility of magnetization and to sudden jumps in the specific heat of the TTF-CA crystal.¹⁸

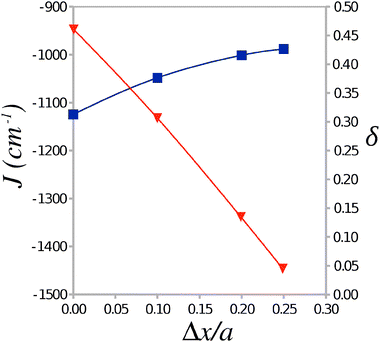Fig. 5 Average value of the Heisenberg exchange integral J and the alternation parameter δ as a function of the displacement Δx/a of the TTF molecule from its position in the 40 K crystal structure.

4. Conclusions

In the present work, magnetic properties of the TTF-CA molecular crystal below the NI transition temperature were studied using the embedded cluster approach²⁰ in combination with a density functional theory method capable of describing the strong non-dynamic electron correlations in molecular systems.^21,24–28 In the low-temperature ionic phase (T = 40 K), the TTF and CA molecules are stacked along the a crystal axis with the distances alternating along the stacking direction.⁹ This leads to the alternating values of the Heisenberg exchange integrals between the unpaired spins on the neighboring TTF⁺ and CA⁻ molecular ions with the average value J = −1124 cm⁻¹ and the alternation parameter δ = 0.46 (see eqn (1)). These values imply that the low-temperature ionic phase of TTF-CA can be described as an alternating antiferromagnetically ordered Heisenberg chain with a finite excitation gap Δ ≈ 560–570 cm⁻¹. Hence, the reported calculations confirm the coexistence of the magnetic and electric long-range order in TTF-CA reported earlier by Giovannetti et al.¹² on the basis of periodic density functional calculations.

Although TTF-CA can formally be qualified as a multiferroic substance, the large excitation gap Δ does not allow to change easily its magnetization in the low-temperature ionic phase.^17,18 However, the magnitude of the gap can be reduced by reducing the value of the Heisenberg exchange integral J and/or by reducing the alternation δ along the stacking axis.^17,18 Thus, stretching the unit cell by 0.5 Å along the a axis results in J = −633 cm⁻¹ and Δ ≈ 310–320 cm⁻¹. A much greater reduction of the gap Δ can be achieved by reducing the alternation parameter δ. A distortion of the low-temperature dimerized crystal structure towards a more symmetric structure with a less pronounced alternation of the TTF–CA distances along the stacking axis results in a considerable reduction of the gap Δ which may eventually collapse for displacements of the order Δx/a ≈ 0.020–0.025 from the experimentally measured molecular positions. At such a distorted structure that may be achieved during the NI transition,⁴ the excitation spectrum of the AF Heisenberg chain should become gapless^17,18 and a non-negligible magnetization may be observed.¹⁷ Besides that, the opening and collapse of the excitation gap Δ should result in a spike in the specific heat as a function of the temperature as was predicted by Jiang et al.¹⁸ Indeed, multiple specific heat anomalies in TTF-CA were experimentally observed near the NI transition temperature by Torrance et al.⁵

The reported theoretical calculations also suggest that a judicious chemical modification may enhance the multiferroic properties of TTF-CA and related compounds. Indeed, increasing the unit cell dimension along the stacking axis and reducing the dimerization in the low-temperature ionic phase may result in experimentally detectable antiferromagnetism of the TTF-CA molecular crystal.

References

1. J. J. Mayerle, J. B. Torrance and J. I. Crowley, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 2988–2995.
2. J. B. Torrance, J. E. Vazquez, J. J. Mayerle and V. Y. Lee, Phys. Rev. Lett., 1981, 46, 253–257.
3. J. B. Torrance, A. Girland, J. J. Mayerle, J. I. Crowley, V. Y. Lee, P. Batail and S. J. LaPlaca, Phys. Rev. Lett., 1981, 47, 1747–1750.
4. J. Hubbard and J. B. Torrance, Phys. Rev. Lett., 1981, 47, 1750–1754.
5. C. Ayache and J. B. Torrance, Solid State Commun., 1983, 47, 789–793.
6. C. S. Jacobsen and J. B. Torrance, J. Chem. Phys., 1983, 78, 112–115.
7. Y. Tokura, H. Okamoto, T. Koda, T. Mitani and G. Saito, Solid State Commun., 1986, 57, 607–610.
8. H. Okamoto, T. Koda, Y. Tokura, T. Mitani and G. Saito, Phys. Rev. B: Condens. Matter, 1989, 39, 10693–10701.
9. M. Le Cointe, M. H. Lemée-Cailleau, H. Cailleau, B. Toudic, L. Toupet, G. Heger, F. Moussa, P. Schweiss, K. H. Kraft and N. Karl, Phys. Rev. B: Condens. Matter, 1995, 51, 3374–3386.
10. S. Koshihara, Y. Takahashi, H. Sakai, Y. Tokura and T. Luty, J. Phys. Chem. B, 1999, 103, 2592–2600.
11. V. Oison, C. Katan, P. Rabiller, M. Souhassou and C. Koenig, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035120.
12. G. Giovannetti, S. Kumar, A. Stroppa, J. van den Brink and S. Picozzi, Phys. Rev. Lett., 2009, 103, 266401.
13. S. Ishibashi and K. Terakura, Phys. B, 2010, 405, S338–S340.
14. K. Tanimura and S. Koshihara, Phase Transitions, 2001, 74, 21–34.
15. A. Girlando, C. Pecile and J. B. Torrance, Solid State Commun., 1985, 54, 753–759.
16. J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640–A658.
17. J. W. Duffy and K. P. Barr, Phys. Rev., 1968, 165, 647–654.
18. Q. Jiang, X. Y. Chen and X. F. Jiang, Phys. Lett. A, 2001, 287, 397–402.
19. I. P. R. Moreira and F. Illas, Phys. Chem. Chem. Phys., 2006, 8, 1645–1659.
20. A. Shukla, M. Dolg, H. Stoll and P. Fulde, Chem. Phys. Lett., 1996, 262, 213–218.
21. M. Filatov and S. Shaik, Chem. Phys. Lett., 1999, 304, 429–437.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
23. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
24. I. P. R. Moreira, R. Costa, M. Filatov and F. Illas, J. Chem. Theory Comput., 2007, 3, 764–774.
25. M. Filatov and S. Shaik, J. Phys. Chem. A, 1999, 103, 8885–8889.
26. D. Cremer, M. Filatov, V. Polo, E. Kraka and S. Shaik, Int. J. Mol. Sci., 2002, 3, 604–638.
27. F. Illas, I. P. R. Moreira, J. M. Bofill and M. Filatov, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 132414.
28. F. Illas, I. P. R. Moreira, J. M. Bofill and M. Filatov, Theor. Chem. Acc., 2006, 116, 587–597.
29. C. W. Murray, N. C. Handy and R. D. Amos, J. Chem. Phys., 1993, 98, 7145–7151.
30. T. V. Russo, R. L. Martin and P. J. Hay, J. Chem. Phys., 1994, 101, 7729–7737.
31. M. Filatov and S. Shaik, Chem. Phys. Lett., 1998, 288, 689–697.
32. I. Okazaki, F. Sato, T. Yoshihiro, T. Ueno and H. Kashiwagi, THEOCHEM, 1998, 451, 109–119.
33. W. J. Hehre, R. Ditchfiel and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
34. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
35. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
36. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
37. C. E. Check, T. O. Faust, J. M. Bailey, B. J. Wright, T. M. Gilbert and L. S. Sunderlin, J. Phys. Chem. A, 2001, 105, 8111–8116.
38. M. C. Cross and D. S. Fisher, Phys. Rev. B: Condens. Matter, 1979, 19, 402–419.

---