Two-stage phase separation in ternary colloid–polymer mixtures

Abstract

Whilst binary colloid–polymer mixtures have been studied in detail over the past few decades, here the first results are presented on a ternary mixture involving two particle sizes. Novel and unusual phase separation kinetics are found, with a liquid phase separating from an aggregate phase.

---

Most studies of depletion interactions in colloidal dispersions, induced by the addition of non-adsorbing polymer, and the resulting phase behaviour of the dispersions, have been concerned with systems of one particle type and size, and also one polymer type and molecular weight. There have been some studies in which binary mixtures of polymers of two different molecular weights have been used,¹ or polymers with a broad molecular weight distribution.² Also dispersions where the particles carried terminally-grafted polymer chains of one type, to which a non-adsorbing polymer of a second type was added, have been investigated.³ However, as far as we are aware, there have been no previous studies of systems containing binary mixtures of particles.

In the work described here, colloidal phase transitions in dispersions of mixtures of monodispersed large (200 nm diameter) and small (30 nm diameter) silica particles in dimethylformamide (DMF), induced by the addition of polystyrene (PS, M_n = 115 000, M_w/M_n = 1.04), up to 50 mg ml⁻¹, have been studied. All the dispersions studied also contained 40 mM lithium chloride (LiCl). This was added in order to reduce the electrical double layer repulsion between the particles, but without leading to instability of the silica in DMF dispersions prior to addition of the polystyrene. This study follows on from a recent publication by us⁴ in which the phase behaviour of the corresponding systems with a single particle type was studied.

The results of the phase equilibration experiments for the binary silica particle systems are summarised in Fig. 1. This takes the form of a phase map, in which the reduced polymer concentration, C_p/C*, is plotted as a function of the vol% ratio of large to small silica particles. C_p is the actual (w/v) concentration used and C* is the polymer overlap concentration, given by,

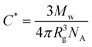where M_w is the weight average molar mass of the polymer chains, N_A is the Avagadro constant and R_g is the radius of gyration of the polymer chains in solution. We have taken a value of R_g = 9.6 nm, which corresponds to DMF being a Θsolvent for polystyrene.⁴ The corresponding value for C* is 54 mg ml⁻¹.

Fig. 1 Phase diagrams for dispersions of binary silica particles in mixtures of polystyrene and DMF, at an overall particle volume fraction of 12%. The three samples discussed in detail are circled.

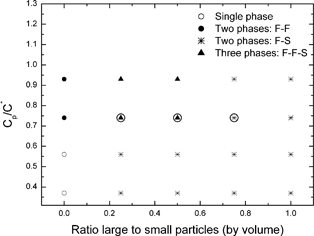
In certain composition ranges for the binary particle systems, three co-existing phases form at equilibrium. The existence of three co-existing phases at equilibrium, even in mixtures of single-size particles and polymers, has been predicted⁵ and observed.^6,7 The present work is, as far as we are aware, the first study of this kind with binary particle mixtures. Fig. 2 shows photographs of the coexisting equilibrium phases for the three samples which are circled in Fig. 1. From just this visual observation, it would seem that the black-coloured, bottom phases are all solid-like and contain particle aggregates; the grey middle phases are fluid-like, and also contain particles; the clear, fluid-like top phases seem to contain very few particles. A more detailed analysis of the actual particle and polymer compositions will be presented later.

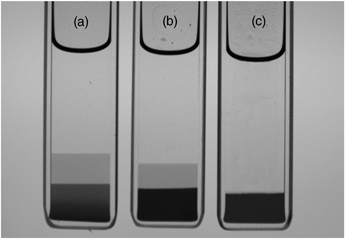Fig. 2 Photographs corresponding to the three equilibrium samples circled in Fig. 1. (a) Three phases at C_p/C* = 0.74 and 1 : 3 large : small particles (by volume); (b) three phases at C_p/C* = 0.74 and 1 : 1 large : small particles; (c) two phases at C_p/C* = 0.74 and 3 : 1 large : small particles. Samples have an internal width of 10 mm and a thickness of 2 mm.

Prior to that it is of interest to comment on how the phases evolve with time. To that end one system was examined in detail; this is the left-most ringed sample in Fig. 1 and the left-most sample in Fig. 2 (i.e. the one containing a volume concentration ratio of 1 : 3 large to small particles, at C_p/C* = 0.74). Within a few minutes this sample split into two co-existing phases: a lower, metastable, solid colloidal phase, consisting of mixed particle aggregates, and a clear upper, fluid phase. Then, in due course, the lower solid, mixed particle phase itself separated into the two states shown in Fig. 2: the (middle) fluid phase and the (bottom) solid aggregate phase. This evolution of the three-phase equilibrium state is illustrated schematically in the table of contents picture.

It is known that, in general, phase transformations do not always proceed initially to the most stable phase (e.g. in molecular crystallisation from the melt or from solution). In 1897 Ostwald postulated his famous “rule of stages”, stating that the phase with the lower, closest free energy should form at first, rather than the one with lowest free energy as such.⁸ Stranski and Totomanow provided an alternative explanation for Ostwald's observation of the formation of intermediate phases. Rather than discussing the various free energy minima, they proposed that the relative heights of the corresponding nucleation free energy barriers were the important consideration, claiming that it is the phase with the lowest nucleation free energy barrier that forms first.⁹ A more recent account of this phenomenon has been provided by Mutaftschiev.¹⁰ Computer simulations, involving one of the current authors, allowed the different nucleation free energy barriers to be calculated, for sufficiently concentrated dispersions of soft spheres which initially form bcc nuclei, whereas fcc is the thermodynamically stable crystal form.¹¹ Very recently experimental evidence for this in colloidal crystallisation was reported.¹² The formation of potentially long-lived metastable polymorphs is of significant commercial interest in the pharmaceutical industry where often one specific crystalline form is patented or approved.

Most commonly the rule of stages is used to describe formation of crystalline phases. Ostwald himself mentioned the possibility of a metastable liquid phase forming as a precursor to a stable crystalline phase. The results we present here represent the first example we are aware of where a fluid phase appears to separate from a (non-crystalline), metastable solid phase.

To obtain further insight into the early stages of the phase separation process, and to test whether our observations could be classified as a true extension of Ostwald's rule of stages, samples were also studied using differential interference contrast (DIC) microscopy. As we showed previously⁴ this technique can clearly distinguish between the formation of fluid-like phases (which appear as droplets initially) and solid-like, aggregate phases.

Fig. 3 shows some typical DIC images of evolving phase structures after 2 min. It is presented in the form of a table, with particle concentration ratio varied along the rows, and C_p/C* up the columns. Column 1 and column 5 show what happens for the pure small particles and the pure large particles, respectively, as we have described before in ref. 4. Columns 2, 3 and 4 correspond to the three (volume) ratios of particle mixtures, as indicated. Let us consider, in particular, the five samples at a C_p/C* value of 0.74 (second row). For the middle three samples in this row, there is a direct correspondence with the three-ringed samples in Fig. 1 and the three photographs in Fig. 2. The image in column 1, (row 2) clearly shows droplets of a liquid phase dispersed in a second, continuous liquid phase. As we showed previously,⁴ these droplets consist mostly of small particles which have separated from the continuous phase containing most of the added polymer. The sample in column 2 (row 2) also contains liquid droplets, but these droplets also contain aggregates of the larger particles, as well as the small particles. In column 3 (row 2), there are similar features, but, because they contain a higher fraction of larger particle aggregates, these “droplets” are distorted in shape, and may already be undergoing some coalescence. In column 4 (row 2), which has the highest ratio of large to small particles, we can only see solid aggregates. Indeed the image here looks very similar to that in column 5 (row 2), which contains only large particles. It is significant that the two samples which eventually form three coexisting phases (Fig. 2) are those in columns 2 and 3 (namely, the left-hand and middle ringed samples in Fig. 1, i.e. at 1 : 3 and 1 : 1 large to small particle volume ratios). We would imagine that the initial, metastable, solid-like phase which appears at the bottom of the sample tube in both these cases after a few minutes, consist of “droplets” which have settled and coalesced, to form a state in which continuous networks of aggregates of large particles exist in a continuous medium of smaller particles. This metastable state then slowly changes on standing. The aggregates of larger particles consolidate at the bottom of the tube, leaving the smaller particles in a liquid-like state as the middle phase. The top phase, which separates initially, is a fluid phase containing mostly polymer. A movie, showing the macroscopic phase evolution for the samples in columns 2, 3 and 4 is provided in the ESI.†

Fig. 3 Typical DIC images of evolving phase structures, two minutes after mixing. The overall particle volume fraction is 12%. The width of each image is 260 μm.

In order to determine the actual compositions of each of the co-existing phases, samples were withdrawn from each of the separated phases, after 10 min and after 24 h (i.e. at equilibrium), and analysed in two ways. Firstly, UV-visible spectral analysis was used to determine the concentrations of PS and large particles (the small particles were found not to contribute significantly to the silica particle peak chosen). Secondly, the withdrawn samples were dried to constant weight. By subtracting the calculated contributions to the solid mass from the PS and large particles, the small particle concentration could also be determined for each phase. The results are shown in Table 1 for the sample at C_p/C* = 0.74 and having a large : small silica ratio of 1 : 3. It can be seen that after 10 min the upper (clear) phase contains only PS and a small percentage of the small silica particles; the lower solid-like phase, already after 10 min, on the other hand, contains most of the small particles and all of the large particles, together with a small amount of PS at a lower concentration than in the upper phase. It is from this lower solid-like phase that the second (middle) fluid phase separates in time. After separating off the lower phase, formed after 10 min, and re-homogenising it, then, within a further 10 min droplets of the future middle phase are already formed, surrounded by a continuous phase containing aggregates (Fig. 4). This supports our contention that, on standing, the (middle) liquid phase separates from the consolidating (bottom) solid aggregate phase. This middle phase, at equilibrium, contains mostly small particles, but with a small percentage of large particles, and a small amount of PS. Somewhat surprisingly, the bottom phase, which remained solid-like, contained large amounts of both large and small particles. Intuitively, one might have expected perhaps that the small particles would mostly have been expelled into the middle phase. What this suggests is that the aggregates in this bottom phase consist of contacts between small and large particles, as well as between large and large particles. It should be remembered, in this context, that the depletion interaction increases with particle size, so that the strength of binary contacts decreases in the order: large–large > large–small > small–small.

Fig. 4 DIC image of lower portion of sample at C_p/C* = 0.74 and 1 : 3 large : small particles (by vol), two minutes after re-homogenizing.

Table 1 Analysis of phase compositions for the sample at C_p/C* = 0.74 and having a large : small silica ratio of 1 : 3

Composition	After 10 min			After 24 h
	C ps/mg ml^−1	C small/mg ml^−1	C large/mg ml^−1	C ps/mg ml^−1	C small/mg ml^−1	C large/mg ml^−1
Top phase	58	24	0	55	19	0
Middle phase	—	—	—	23	510	38
					(Φ = 0.26)	(Φ = 0.02)
Bottom phase	14	550	169	3.2	697	379
		(Φ = 0.28)	(Φ = 0.08)		(Φ = 0.35)	(Φ = 0.19)
Overall concentration	40	228	67	40	228	67
		(Φ = 0.11)	(Φ = 0.03)		(Φ = 0.11)	(Φ = 0.03)

---

It should be noted that the figures quoted in Table 1 are only accurate to within about 10% as it was observed that some of the silica particles had stuck to the walls of the glass cells. This is not surprising as the depletion interaction is stronger between a flat surface and a sphere than between two spheres. Indeed one of us has noticed this wall effect previously.¹³

Qualitative confirmation of the data listed in Table 1, for the relative ratios of large to small particles in the (equilibrium) middle and bottom phases for the sample at C_p/C* = 0.74 and having a large : small silica ratio of 1 : 3, is given in TEM image in the ESI.† This shows electron micrographs of the two dried samples. Although one must, of course, be aware of artefacts produced as a result of drying and sampling, it can be seen that the concentration of small silica particles is similar in both the middle and bottom phases, but that the concentration of large particles is greater in the bottom phase than in the middle one.

Conclusions

Mixtures of charged silica particles and a non-adsorbing polymer (polystyrene) in dimethylformamide (DMF) have been studied. DMF is a near-theta solvent for the polymer. Lithium chloride was added to reduce the electrical double layer repulsion between the particles. At certain compositions, three co-existing equilibrium phases evolved. The (clear) top phase and the (slightly turbid) middle phase were both fluid-like, whilst the bottom (opaque) phase was solid-like, containing particle aggregates. What was most unexpected and novel, however, was the manner in which the phases evolved. After a few minutes only two phases had appeared: an upper, fluid-like clear phase and an opaque, solid-like, bottom phase. It was from this lower solid-like phase that the fluid-like middle phase gradually separated. It is thought that this is the first reported example of a fluid phase separating from a metastable solid phase. This seems to be an extension of Ostwald's step rule. We are currently extending these studies to cover a larger range of system parameters, in order to build up a more complete picture of the phase evolution behaviour of binary mixtures of silica particles undergoing depletion flocculation in DMF with added polystyrene. Previously we reported that the behaviour of the binary colloid–polymer mixtures is in good agreement with recent theoretical predictions for charged particles by Gögelein and Tuinier.^4,14 An extension of the theory to encompass ternary mixtures is therefore desirable.

Acknowledgements

We should like to thank AkzoNobel and EPSRC for the provision of a Dorothy Hodgkin research studentship for JZ, and Simon Davies and Simon Emmett of AkzoNobel for helpful discussions. We thank Paul Bartlett for access to the video camera setup.

References

1. P. Jenkins and B. Vincent, Langmuir, 1996, 12, 3107–3113.
2. J. J. Lietor-Santos, C. Kim, M. L. Lynch, A. Fernandez-Nieves and D. A. Weitz, Langmuir, 2010, 26, 3174–3178.
3. A. Milling, B. Vincent, S. Emmett and A. Jones, Colloids Surf., 1991, 57, 185–195.
4. J. Zhou, J. S. van Duijneveldt and B. Vincent, Langmuir, 2010, 26, 9397–9402.
5. H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, Europhys. Lett., 1992, 20, 559–564.
6. S. M. Ilett, A. Orrock, W. C. K. Poon and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1344–1352.
7. M. A. Faers and P. F. Luckham, Langmuir, 1997, 13, 2922–2931.
8. W. Ostwald, Z. Phys. Chem. (Leipzig), 1897, 22, 289–330.
9. I. N. Stranski and D. Z. Totomanow, Phys. Chem., 1933, 163, 399–408.
10. B. Mutaftschiev, Nucleation theory, in Handbook of Crystal Growth, ed. D. T. J. Hurle, Elsevier, Amsterdam, 1993, vol. 1a, ch. 4, pp. 187–247.
11. J. S. van Duijneveldt and D. Frenkel, J. Chem. Phys., 1992, 96, 4655–4688.
12. S. H. Xu, H. W. Zhou, Z. W. Sun and J. C. Xie, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2010, 82, 010401.
13. S. Rawson, K. Ryan and B. Vincent, Colloids Surf., 1988, 34, 89–93.
14. C. Gögelein and R. Tuinier, Eur. Phys. J. E, 2008, 27, 171–184.

---

Footnote

† Electronic supplementary information (ESI) available: Video showing the time evolution of the three samples presented in Fig. 2, experimental details, and TEM images. See DOI: 10.1039/c0cp01523g

---