High-resolution solid-state 13C μMAS NMR with long coherence life times†
Suresh K.
Vasa
,
Hans
Janssen
,
Ernst R. H.
Van Eck
and
Arno P. M.
Kentgens
*
Institute for Molecules and Materials, Radboud University Nijmegen, Heyendaalseweg 135, 6525 ED Nijmegen, The Netherlands. E-mail: S.Vasa@nmr.ru.nl; Fax: +31 24 3652112; Tel: +31 24 3652678
First published on 12th November 2010
Abstract
Longer coherence life times (i.e. smaller homogeneous linewidths) can be achieved for carbon resonances which are strongly coupled to protons with high rf field heteronuclear decoupling in micro magic angle spinning NMR. Better proton decoupling enhances the sensitivity and resolution of two-dimensional through-bond correlation experiments for mass-limited samples with uniform carbon labeling.
Solid-state NMR spectroscopy has become an important tool in solid-state chemistry and materials science for determining structural information. The primary limitations for the application of solid-state NMR to mass-limited samples are sensitivity and resolution. The sensitivity is routinely improved by cross-polarization experiments along with Magic Angle Spinning (MAS). The microcoil probe heads developed in our group alleviate the sensitivity and resolution problem for studying nano-liter volume solid samples.1,2 Added advantages of the microcoil probe heads are the availability of very high rf field strengths at very low power for both protons and X-nuclei. A further bonus is its ability to study single micro crystals.3,4 This can be exploited to get resolution beyond the capabilities of current solid-state NMR probeheads.
The determining factor for obtaining high-resolution spectra of rare spins such as 13C in protonated materials is proton decoupling. There exists a variety of heteronuclear decoupling sequences in the literature, enhancing the resolution of rare spin spectra under MAS.5–9 It has been shown for 13CH2 of glycine, which is strongly coupled to protons that even when the limiting line width has been reached, decoupling sequences continue to lengthen the transverse dephasing times that determine the sensitivity of many multidimensional or multipulse experiments.10 Here we explore the limits of these transverse dephasing times for carbons strongly coupled to protons by increasing the decoupling field strength in a number of popular heteronuclear decoupling sequences. We observe that dephasing times can be prolonged to hundreds of milliseconds far beyond the current state of the art and demonstrate that this significantly improves the sensitivity and resolution of solid-state 2D experiments.
Fig. 1a shows the microMAS sample holder filled with 2-13C–15N Glycine powder and a total volume of 70 nL. It has been observed that the line width improves and the intensity of the proton decoupled 13C resonance line increases when using phase modulated decoupling sequences like two-pulse phase-modulation (TPPM)5 or small phase incremental alteration (SPINAL-64)9 compared to simple continuous wave (CW) decoupling for a given rf field strength. It is also observed that, above a certain rf field strength (120 kHz in the present case) the linewidth and intensity do not change significantly for TPPM and SPINAL (see Fig. S1 in ESI†). As reported earlier,6 there are both homogeneous and inhomogeneous contributions to this residual linewidth (Δ* = 1/πT2*). Various contributions to the linewidth can be classified as follows: (i) broadening arising from incomplete averaging of hetero nuclear dipolar couplings by magic angle spinning and decoupling by rf: (ii) broadening due to transverse relaxation induced by possible fluctuations in the dipolar network, analogous to liquid-state NMR, due to “incoherent motions”: and (iii) broadening due to distributions of chemical shifts arising from structural disorder, B0 inhomogeneity and anisotropic bulk magnetic susceptibility (ABMS)11 effects.
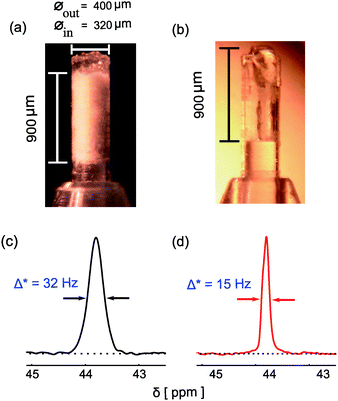 | ||
| Fig. 1 The micro sample holder filled with (a) 2-13C–15N Glycine powder (b) 2-13C–15N Glycine single crystal and dimension of the sample in the sample holder are specified. Proton decoupled 13C CPMAS spectrum of (c) glycine powder (d) glycine single crystal using SPINAL decoupling sequence at a rf field strength of 394 kHz and a spinning speed of 10 kHz. All the experiments were done using a homebuilt 2.5 mm piggy-back microMAS probe3 using a VNMRS console at 9.4 T field. | ||
To investigate the importance of latter terms, we compared the 1H decoupled 13C linewidth of the 13CH2 in glycine for a powder and a spinning single crystal, giving a line width of 32 Hz and 15 Hz respectively (Fig. 1). The latter value being limited by susceptibility broadening induced by the probe (for more details see ESI†). For materials with a non-zero ABMS, MAS is not effective in averaging the field variations due to crystal boundaries and voids in a powder and thus line broadening arises. Furthermore the structure of the material might be better defined in a micro crystal as compared to a powder, especially with very small grain sizes. These factors may well explain the line-narrowing by a factor of 2 when a single crystal is used instead of a powder, underscoring the attractiveness of single crystal microMAS to get highly resolved spectra.
Using a simple spin-echo sequence (Fig. 2a), inhomogeneous contributions to the residual linewidth can be refocused. The contribution due to incoherent motions is expected to be small in rigid solids, leaving the residual heteronuclear dipolar couplings to dominate dephasing of 13C magnetization. We investigated the coherence lifetimes (T2′ = 1/Δ2′ where Δ2′ is the homogeneous linewidth) of 13CH2 in glycine under rf decoupling using the CW, TPPM and SPINAL sequences (Fig. 2b). All the decoupling parameters were optimized using the echo signal intensity at 2τecho = 40 ms. Coherence lifetimes obtained at different rf decoupling field strengths with various sequences are shown in Table 1. It can be observed that the coherence lifetimes increase with rf field strength for all the sequences. For both TPPM and SPINAL, there is no significant improvement in the T2′ values after a certain rf decoupling field strength is reached whereas CW keeps improving with increasing rf-field strength. SPINAL performs much better than TPPM and CW at high rf field conditions.
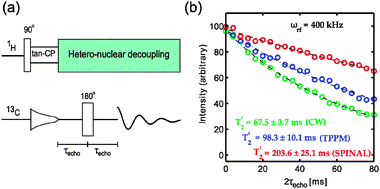 | ||
| Fig. 2 (a) The spin-echo sequence used for measuring coherence lifetimes. (b) Experimentally measured decay curves for 13CH2 of glycine (‘circles’) and fitted with exponentially decay function (‘dashed lines’) for various sequences at a decoupling field strength of 400 kHz and a spinning speed of 10 kHz. | ||
| Power (in watt) | ν rf (in kHz) | CW (T2 in ms) | TPPM (T2 in ms) | SPINAL (T2 in ms) |
|---|---|---|---|---|
| 0.1 | 80 | 5 ± 1 | 34 ± 5 | 27 ± 4 |
| 0.3 | 120 | 12 ± 2 | 74 ± 12 | 105 ± 11 |
| 1.2 | 247 | 40 ± 4 | 105 ± 10 | 191 ± 18 |
| 3.1 | 394 | 68 ± 4 | 98 ± 10 | 204 ± 25 |
At 400 kHz, we observed a coherence lifetime of 200 ms using SPINAL which is 4 times longer than previously reported10,12 (Fig. 2b). In other words, we could get a refocused homogeneous linewidth of 1.6 Hz (0.02 ppm @400 MHz). Similar coherence life times were observed in both powder and single crystal. Varying the spinning speed between 5 and 18 kHz hardly affects the observed T2′. A significant improvement from 200 ms to 250 ms was observed by restricting the sample to 250 μm (total sample volume = 20 nL) at the center of the coil (800 μm), showing the importance of rf inhomogeneity compensated decoupling sequences. Unfortunately experiments on the usage of decoupling sequences such as eDROOPY and adiabatic sequences are restricted by the spectrometer limitations for handling the faster phase modulations at high rf field strengths.
The long coherence lifetimes can be exploited in the sequences such as refocused INADEQUATE10 experiments under proton decoupling. Fig. 3a shows the aliphatic region of the 2D refocused INADEQUATE spectrum of [U–13C, 15N] L-isoleucine, showing the 13C–13C through-bond correlations for a sample volume of 70 nL and the total experimental time was 37 h. The spectrum clearly shows two resonances for each CγH3, CδH3 and CγH2 (resulting from two crystallographically in-equivalent molecules in the unit cell) and their corresponding through-bond correlations. The two CγH2 resonances are not resolved at lower decoupling rf field strengths.13Fig. 3b shows the enhancement in the sensitivity of different F2 slices of 2D spectra by increasing the decoupling field strength from 80 kHz to 400 kHz. A sensitivity gain around 3 was observed for CH2 and an overall gain of 2 was obtained for 2D at higher field strength.
![(a) Two dimensional refocused INADEQUATE 13C spectrum of [U–13C, 15N] l-isoleucine (sample volume = 70 nL) acquired at a spinning speed of 12.5 kHz and the SPINAL decoupling field strength of 400 kHz @ 3 W (more details in ESI). The skyline projection along single quantum dimension is shown on the top. (b) A comparison of different slices along single quantum dimension of 2D INADEQUATE spectra acquired using SPINAL decoupling at different rf field strengths of 80 kHz, 120 kHz and 400 kHz. The absolute intensities (in arbitrary units) of the some of the peaks are shown on the top.](/image/article/2011/CP/c0cp01929a/c0cp01929a-f3.gif) | ||
| Fig. 3 (a) Two dimensional refocused INADEQUATE 13C spectrum of [U–13C, 15N] L-isoleucine (sample volume = 70 nL) acquired at a spinning speed of 12.5 kHz and the SPINAL decoupling field strength of 400 kHz @ 3 W (more details in ESI†). The skyline projection along single quantum dimension is shown on the top. (b) A comparison of different slices along single quantum dimension of 2D INADEQUATE spectra acquired using SPINAL decoupling at different rf field strengths of 80 kHz, 120 kHz and 400 kHz. The absolute intensities (in arbitrary units) of the some of the peaks are shown on the top. | ||
To conclude, we showed that the high rf field strengths attainable at very low power using microMAS make it possible to significantly prolong transverse dephasing times in rigid solids. For powders, the resolution of the 13C spectrum in the direct dimension is limited by ABMS, whereas for crystals we get better resolution. MicroMAS is an ideal tool for studying micro crystals (e.g. micro crystalline proteins) with high resolution similar to liquid spectra. The longer dephasing times achieved with high rf decoupling will increase the sensitivity of many 2D experiments like INADEQUATE, J-related experiments,14,15 many bond correlations, RFDR and REDOR type experiments for accurate long distance measurements.16 For disordered materials, huge sensitivity enhancements can be obtained using these kinds of 2D experiments.
Acknowledgements
We thank A. Brinkmann for useful discussions. This research is supported by The Netherlands organization for scientific research (NWO) TOP grant.References
- H. Janssen, A. Brinkmann, E. R. H. van Eck, P. J. M. van Bentum and A. P. M. Kentgens, J. Am. Chem. Soc., 2006, 128, 8722–8723 CrossRef CAS.
- A. P. M. Kentgens, J. Bart, P. J. M. van Bentum, A. Brinkmann, E. R. H. Van Eck, J. G. E. Gardeniers, J. W. G. Janssen, P. Knijn, S. Vasa and M. H. W. Verkuijlen, J. Chem. Phys., 2008, 128, 052202 CrossRef CAS.
- A. Brinkmann, S. K. Vasa, H. Janssen and A. P. M. Kentgens, Chem. Phys. Lett., 2010, 485, 275–280 CrossRef CAS.
- S. K. Vasa, E. R. H. van Eck, J. W. G. Janssen and A. P. M. Kentgens, Phys. Chem. Chem. Phys., 2010, 12, 4813–4820 RSC.
- A. E. Bennett, C. M. Rienstra, M. Auger, K. V. Lakshmi and R. G. Griffin, J. Chem. Phys., 1995, 103, 6951–6958 CrossRef.
- G. De Paepe, P. Hodgkinson and L. Emsley, Chem. Phys. Lett., 2003, 376, 259–267 CrossRef CAS.
- A. Detken, E. H. Hardy, M. Ernst and B. H. Meier, Chem. Phys. Lett., 2002, 356, 298–304 CrossRef CAS.
- M. Eden and M. H. Levitt, J. Chem. Phys., 1999, 111, 1511–1519 CrossRef CAS.
- B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101 CrossRef CAS.
- G. De Paepe, N. Giraud, A. Lesage, P. Hodgkinson, A. Bockmann and L. Emsley, J. Am. Chem. Soc., 2003, 125, 13938–13939 CrossRef CAS.
- D. L. Vanderhart, W. L. Earl and A. N. Garroway, J. Magn. Reson., 1981, 44, 361–401 CAS.
- S. Antonijevic and G. Bodenhausen, Angew. Chem., Int. Ed., 2005, 44, 2935–2938 CrossRef CAS.
- A. Lesage, C. Auger, S. Caldarelli and L. Emsley, J. Am. Chem. Soc., 1997, 119, 7867–7868 CrossRef.
- W. Bermel, I. C. Felli, R. Kummerle and R. Pierattelli, Concepts Magn. Reson., 2008, 32A, 183–200 Search PubMed.
- S. Laage, A. Lesage, L. Emsley, I. Bertini, I. C. Felli, R. Pierattelli and G. Pintacuda, J. Am. Chem. Soc., 2009, 131, 10816 CrossRef CAS.
- G. Pileio, S. Mamone, G. Mollica, I. M. Montesinos, A. Gansmuller, M. Carravetta, S. P. Brown and M. H. Levitt, Chem. Phys. Lett., 2008, 456, 116–121 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: More details of the optimized parameters for decoupling sequences and 2D INADEQUATE. See DOI: 10.1039/c0cp01929a |
| This journal is © the Owner Societies 2011 |
