DOI:
10.1039/C0EE00312C
(Review Article)
Energy Environ. Sci., 2011,
4, 73-82
Solar-driven gasification of carbonaceous feedstock—a review
Received
28th July 2010
, Accepted 28th September 2010
First published on 26th October 2010
Abstract
Given the future importance of solid carbonaceous feedstocks such as coal, coke, biomass, bitumen, and carbon-containing wastes for the power and chemical industries, gasification technologies for their thermochemical conversion into fluid fuels are developing rapidly. Solar-driven gasification, in which concentrated solar radiation is supplied as the energy source of high-temperature process heat to the endothermic reactions, offers an attractive alternative to conventional autothermal processes. It has the potential to produce high-quality synthesis gas with higher output per unit of feedstock and lower specific CO2 emissions, as the calorific value of the feedstock is upgraded through the solar energy input by an amount equal to the enthalpy change of the reaction. The elimination of an air separation unit further facilitates economic competitiveness. Ultimately, solar-driven gasification is an efficient means of storing intermittent solar energy in a transportable and dispatchable chemical form. This review article develops some of the underlying science, examines the thermodynamics and kinetics of the pertinent reactions, and describes the latest advances in solar thermochemical reactor technology.
Broader context
Solar-driven gasification makes use of concentrated solar energy to thermochemically convert solid carbonaceous feedstock into high-quality synthesis gas—mainly a mixture of H2 and CO that can be further processed to liquid fuels—with higher output per unit of feedstock and lower specific CO2 emissions than conventional authothermal gasification. Intermittent solar energy is thus efficiently stored in a transportable and dispatchable chemical form and can free industrial nations from oil imports by utilizing domestic resources. Particular progress has been made in the area of solar-thermal reactor engineering. Solar reactor prototypes based on packed-bed and entrained-flow concepts have been demonstrated at high temperatures (>1400 K) in solar furnaces and their fundamental heat/mass transfer modeling indicates promising performance and high solar-to-fuel energy conversion efficiency at larger scales. The first generation of industrial solar gasification pilot plants using solar tower concentrating systems is coming into operation. They create a link between today's fossil-fuel-based technology and tomorrow's solar chemical technology and offer a viable transition path to solar fuels production.
|
Introduction
Thermochemical gasification transforms solid carbonaceous feedstocks into widely applicable, clean and energy rich synthesis gas (syngas)—mainly H2 and CO—and has the potential to free industrial nations from liquid fuel imports by utilizing domestic solid resources. Uses currently focus on application to IGCC power systems, conversion to liquid fuels, and hydrogen production.1–3 Solar-driven gasification is well positioned to produce synthesis gas of high quality by using concentrated solar radiation as the energy source of process heat. Conventional autothermal gasification requires a portion of the injected feedstock mass to be combusted internally with pure O2 to supply high-temperature process heat for the endothermic reactions. For example, 12 MJ kg−1 are required to steam-gasify a typical bituminous coal of LHV 34 MJ kg−1.4 Thus, at least 35% of the injected coal mass must be burned uniquely to power the reaction, which inherently decreases coal utilization and contaminates the product gases with combustion products. In contrast, solar-driven steam-gasification is free of combustion byproducts and yields higher syngas output per unit of feedstock. Based on the stoichiometric gasification of pure carbon, the product syngas may have up to 33% lower CO2 intensity because its calorific value is solar-upgraded over that of the original carbon feedstock by an amount equal to the enthalpy change of the endothermic reaction, while retaining the same amount of carbon. A 2nd-law (exergy) analysis indicated that combined Brayton–Rankine power cycles running on solar-made syngas can double the specific electric output per unit mass of coal and consequently achieve specific CO2 intensities of 0.49–0.56 kg CO2/kW he—approximately half that of conventional coal-fired power plants.4,5 If biomass is used as a feedstock, the syngas produced may be considered CO2-neutral. Ultimately, solar-driven gasification is a means of storing intermittent solar energy in a transportable and dispatchable chemical form.6
Although coal is the main feedstock candidate, carbonaceous wastes have also been investigated in the laboratory and in modern waste-to-energy (WTE) systems running autothermal gasifiers.7–9 These studies showed that not only were the typical volume reduction benefits and ash neutralization of incinerators achieved but dioxin emissions were halved and efficiencies of WTE systems were improved by up to 50%.8 For a variety of waste fuels, 75–85% of the introduced feedstock's energy content was captured in the syngas.7 However, the combustion products needed to be separated from the off gas, cleaned, and released to the environment. Solar-driven gasification could be well applied to dealing with waste disposal and neutralization as well as fuel recovery.
In contrast to conventional autothermal gasifiers, solar reactors are subject to thermal transients due to intermittent solar irradiation. Structural ceramic materials used for applications in excess of 1300 K, such as siliconized/sintered SiC and SiC-coated graphite, have demonstrated stable performance during thermal cycling and thermal shocks in laboratory tests.10 Transient solar power input may also produce short term peaks in syngas production, requiring sizing off-gas handling equipment for surplus capacity. This phenomenon may be particularly strong in feedstocks with high volatile contents upon the introduction of fresh charges, as is the case with waste carbonaceous materials. Solar reactor concepts have the potential to be hybridized to allow nighttime operation, especially in allothermal processes that use hot secondary mediums,11,12 but at the expense of introducing complexity in reactor designs and logistics. Furthermore, the full deployment of solar gasification may be complicated by the fact that water resources are inherently poor in arid regions with vast solar resources (>2000 kWh m−1 per year).
Thermodynamics
The steam-gasification of carbonaceous feedstocks involves principally two chemical processes: pyrolysis and char gasification, both of which are critical in the handling of carbonaceous fuels over a wide temperature range. The overall net reaction for stoichiometric water delivery can be represented by:1,4| | 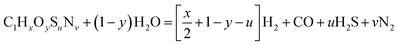 | (1) |
where x, y, u and v are the elemental molar ratios of H/C, O/C, S/C and N/C in the feedstock. Mineral matter, intrinsic water content, and other impurities contained in the feedstock are omitted from consideration in eqn (1). Their presence may have an effect on the kinetics and final product composition, but their exclusion does not affect the main conclusions of this analysis. Pyrolysis, occurring typically in the temperature range 450–900 K, involves the thermal decomposition of bonds within the carbonaceous chain and release of hydrogen rich gaseous (CH4, C2H6, etc.) and condensable (tars) compounds, while the fixed carbon portion of the feedstock forms char—effectively pure solid carbon. The net pyrolysis reaction can be represented by:| | 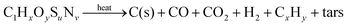 | (2) |
Pyrolysis has been extensively studied empirically for various coal ranks ranging from anthracite (∼10 wt% volatile matter) to peat (>65 wt% volatile matter), as well as for scrap tires, plastics, biomass, and refuse derived fuels.13–17 Solar-driven pyrolysis was investigated in early studies on biomass and coal.18–21 Subsequent to pyrolysis, char serves as the reactant for the highly endothermic carbon-steam gasification reaction,
| | | C(s) + H2O = CO + H2, ΔH°298K = 131 kJ mol−1 | (3) |
Favorable conditions for this reaction are temperatures above 1100 K, where the reaction kinetics is fast and equilibrium is entirely on the side of the products.
Eqn (3) summarizes the overall reaction, but a number of intermediate competing reactions need to be considered:
| | | C(s) + CO2 = 2CO, ΔH°298K = 172 kJ mol−1 | (4) |
| | | C(s) + 2H2 = CH4, ΔH°298K = −75 kJ mol−1 | (5) |
| | | CH4 + H2O = CO + 3H2, ΔH°298K = 206 kJ mol−1 | (6) |
| | | CO + H2O = CO2 + H2, ΔH°298K = −42 kJ mol−1 | (7) |
The Boudouard reaction, eqn (4), becomes important for CO2-based gasification at above 1000 K, while CH4 cracking, eqn (5), and CH4 reforming, eqn (6), proceed catalytically at above 900 K. Of particular interest is the water–gas shift reaction (WGSR), eqn (7), which allows tuning the syngas composition destined for catalytic reforming to liquid fuels (e.g. Fischer–Tropsch synthesis). The WGSR equilibrium is shifted to the reactants at high temperatures and is therefore conducted with added catalysts at low temperatures. All these reactions depend strongly on temperature, pressure, and residence times in a solar reactor, and their combination yields the final product gas composition. As an example, the equilibrium composition of reacting beech charcoal (C1H0.47O0.055S0.022N0.004) with stoichiometric water per eqn (1) is shown in Fig. 1 at 1 bar.22 Species with mole fractions lower than 10−3 (e.g., H2S, HCN) are omitted. At temperatures below about 800 K, the formation of CH4 and CO2 is thermodynamically favored but unlikely to proceed due to kinetic limitations. The reaction goes to completion at above 1200 K producing a syngas mixture of 53% H2 and 47% CO. For higher, industrially preferred pressures, the equilibrium is shifted towards the reactants according to Le Châtelier's principle, as shown in Fig. 2 for beech charcoal gasification as a function of pressure at 1000 K (Fig. 2a) and as a function of temperature at 10 bar (Fig. 2b).
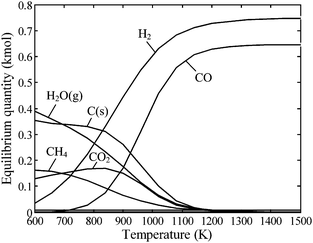 |
| | Fig. 1 Equilibrium composition as a function of temperature of the stoichiometric system of eqn (1) for beech charcoal C1H0.47O0.055S0.022N0.004 at 1 bar. Species with mole fractions less than 10−3 have been omitted. | |
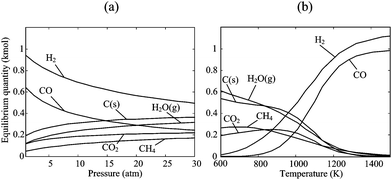 |
| | Fig. 2 Equilibrium composition of the stoichiometric system of eqn (1) for beech charcoal C1H0.47O0.055S0.022N0.004: (a) as a function of pressure at 1000 K, and (b) as a function of temperature at 10 bar. Species with mole fractions less than 10−3 have been omitted. | |
The specific enthalpy change of eqn (1), ΔHR, can be calculated by assigning a reference enthalpy to [C(s) + (x/2)H2 + (y/2)O2 + uS + (v/2)N2] at 298 K and further adjusting for the offset between the reported heating value of the carbonaceous feedstock and the enthalpy change of the combustion reaction at 298 K:4,22
| | 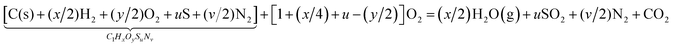 | (8) |
Fig. 3 shows ΔHR of eqn (1) as a function of temperature for the steam-gasification of beech charcoal and three waste feedstocks: industrial sludge (a mixture of inks, dyes, solvents, and paints), sewage sludge, and tire powder. The reactants are assumed to be fed in at 298 K and products—having an equilibrium composition—recovered at the reaction temperature T. The variation of ΔHR at low temperatures (∼600 K) is determined by the various compositions of the feedstocks and their resulting equilibrium compositions. The strong rise in ΔHR between 700 and 1100 K is mainly driven by the changing composition of the product gas as the H2 and CO mole fractions increase. Because the product gas composition no longer changes beyond 1200 K, the further increase in ΔHR is driven by the latent heat of H2 and CO. Operational optimization of solar reactors hinges on determining an optimal temperature where thermal losses, reaction rates, and reaction enthalpies combine to produce the highest energy conversion efficiency. Though kinetic rates improve above 1200 K, re-radiation losses increase markedly while product composition remains unaffected.
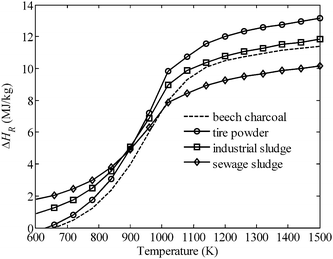 |
| | Fig. 3 Specific enthalpy change ΔHR of eqn (1) for various carbonaceous feedstocks, with reactants fed in at 298 K and products—having an equilibrium composition—recovered at the reaction temperature T. | |
Kinetics
The proposed gasification kinetic model is based on the oxygen-exchange mechanism describing reversible O-transfer surface reactions followed by a unidirectional gasification step, and on reversible steam sorption as OH/H groups with irreversible surface chemistry.23,24 A set of kinetic rate expressions of the Langmuir–Hinshelwood type are formulated to describe the formation and consumption of each gas species,| | 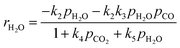 | (9) |
| | 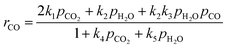 | (11) |
| | 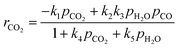 | (12) |
| | 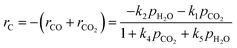 | (13) |
ri is the reaction rate of species i (i = H2, H2O, CO, CO2 and C) for heterogeneous surface reactions, defined as:| | 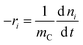 | (14) |
where mC is the mass of carbon. The temperature dependence of rate constants is determined by the Arrhenius law:| | 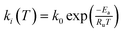 | (15) |
Apparent activation energies and frequency factors were experimentally obtained by thermogravimetric measurements for petroleum coke (petcoke).23 In order to account for mass transfer limitations inside the solid particle for varying particle diameter D, an experimentally determined particle effectiveness factor was introduced:25
| | | ξ(D) = 0.571e−1.29×104D + 0.429e−9.56×102D | (16) |
ξ converges to 1 for
D approaching 0 and diffusion becoming instantaneous. For a poly-disperse medium,
ξ is evaluated at the equivalent mono-disperse diameter
Dξ,
| | 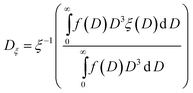 | (17) |
where
ξ−1 denotes the inverse function of
eqn (16). A simplified empirical approach for the combined
pyrolysis and
gasification of carbonaceous feedstocks containing important volatile contents (
e.g. carbonaceous wastes) has been formulated based on the sum of 1
st-order reactions of
N pseudo-components:
26| | 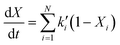 | (18) |
where
Xi =
xi(
T,
t)/
xt=∞,i and
xi(
T,
t) denotes the mass fraction of pseudo-component
i having reacted until temperature
T and time
t, and
xt=∞,i is the total mass fraction of pseudo-component
i.
ki′ is assumed to obey the Arrhenius law (
eqn (15)). This modeling scheme has been applied for the steam
gasification of sewage sludge, industrial sludge (a dewatered mixture of inks,
dyes and paints), fluff (mixture of papers, plastics and textiles), and scrap tire powder
26 as well as for the
pyrolysis of petcoke.
23
Low volatile, high fixed carbon content feedstocks are best suited for solar gasification as they lead to the largest solar-upgrade of their calorific value (see eqn (21)) and best utilize the high temperatures achieved. The ability to avoid tar formation is a major advantage since temperatures exceeding 1500 K can be achieved with concentrated solar energy. Physical factors such as ash content and particle size play an equally important role in the correct matching of reactor types to feedstocks,27 as shown in the next section. Catalyzed gasification reactions proceed at lower temperatures, however, they are generally avoided in commercial applications due to the complexity of separating and recovering the catalyst from the ash.28,29
Solar reactor technology
Solar reactors for high-temperature thermochemical applications usually make use of cavity-type configurations to capture effectively the incident concentrated solar radiation entering through the aperture.6 Because of multiple internal reflections, the fraction of the incoming energy absorbed by the cavity greatly exceeds the surface absorptance of the inner walls. The solar energy absorption efficiency, ηabsorption, is defined as the net rate at which energy is being absorbed divided by the concentrated solar power through the aperture. For a perfectly insulated cavity-receiver (neglected convection/conduction heat losses), it is given by:30| | 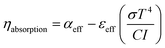 | (19) |
where αeff and εeff are the effective absorptance and emittance of the solar cavity-receiver, respectively, σ is the Stefan–Boltzmann constant, T is the nominal reactor temperature, I direct normal solar irradiation, and C is mean solar flux concentration ratio over the aperture.† As the ratio of the cavity's characteristic length to the aperture diameter increases, the cavity-receiver approaches a blackbody absorber: αeff = εeff = 1. Smaller apertures also reduce re-radiation losses; however, they intercept less sunlight requiring higher concentrations to arrive at a desired power. Consequently, the optimum aperture size becomes a compromise between maximizing radiation capture and minimizing radiation losses.30 To some extent, the aperture size may be reduced with the help of non-imaging secondary concentrators, e.g. compound parabolic concentrators (CPCs31), incorporated at the receiver's aperture.
The net absorbed concentrated solar energy drives the endothermic gasification reaction. The measure of how well the solar energy input is converted into the chemical energy of the syngas produced is the solar-to-fuel energy conversion efficiency, defined as:
| | 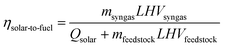 | (20) |
where
Qsolar is the total solar energy delivered through the receiver's aperture over the duration of the experimental run,
mfeedstock and
msyngas are the gasified feedstock and evolved syngas mass, respectively, integrated over the duration of the experimental run, and
LHV is the low heating value of the feedstock,
e.g. about 35
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
700 kJ kg
−1 for
anthracite. The energetic upgrade factor is defined as the ratio of the heating value of the syngas produced to that of the feedstock processed:
| | 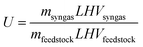 | (21) |
For the stoichiometric system C +
H2O, the equilibrium composition at 1300 K consists of an equimolar mixture of H
2 and CO, for which
U = 1.33.
Solar gasification reactors may be classified as:6 (1) directly irradiated reactors, where the solid carbonaceous reactants are directly exposed to the concentrated solar irradiation; and (2) indirectly irradiated reactors, where heat is transferred to the reaction site through an opaque wall. While directly irradiated reactors provide efficient heat transfer directly to the reaction site, they require a transparent window for the access of concentrated solar radiation, which becomes a critical and troublesome component under high-pressures, severe gas environments, and particularly at large scales. High operating pressures require shaped windows, e.g. conical32 and hemispherical.33 The alternative downstream compression of solar syngas for Fischer–Tropsch and Haber–Bosch processes and for gas turbine applications represents an up to 4 times higher energy expenditure.1 On the other hand, the implementation of spectrally selective windows, such as fused quartz, with high transmissivity in the solar spectrum around 0.5 µm where the solar irradiation peaks, and high reflectivity in the infrared range around 1.93 µm where the Plank's spectral emissive power for a 1500 K blackbody peaks, can diminish significantly re-radiation losses and, consequently, augment ηabsorption. Indirectly irradiated reactors eliminate the need for a window at the expense of having less efficient heat transfer—by conduction—through the walls of an opaque absorber. Thus, the disadvantages are linked to the limitations imposed by the materials of the absorber, with regard to maximum operating temperature, inertness to the chemical reaction, thermal conductivity, radiative absorptance, and resistance to thermal shocks.
Early studies on solar gasification used packed-bed reactors which mimicked the operation of the gravity fed Lurgi reactor in which the feedstock charge moves in a counter-flow to the reacting gas; progressively drying, pyrolyzing, gasifying, and finally slagging ashes for removal.18,19 Packed beds were further applied for kinetics studies as functions of particle size, temperature, and moisture content.34,35 Packed bed reactors are generally simple, robust, can accommodate a wide range of feedstock sizes and forms, and do not require excess steam flows, making them correspondingly cheap. Their main drawback is associated with the rate of heat/mass transfer through the porous packed bed which limits the reaction rate and throughput.36 Additionally, ash buildup decreases the surface absorptivity of the irradiated packed bed and may lead to slagging and sintering, particularly for high ash content feedstocks. In contrast, fluidized-bed reactors achieve efficient mass and heat transfer at the expense of requiring feedstock preparation with small particles—typically less than 5 mm—and narrow particle size distributions.37–41 Additionally, excess (over-stoichiometric) steam or inert gas is often necessary to achieve fluidization, which translates into an energy penalty while displacing possible syngas production with a given allowable bed pressure drop.11 Recently, innovative reactor designs based on packed beds and entrained flows have been proposed and experimentally demonstrated for the combined pyrolysis and gasification of petcoke, biomass charcoal, coal, and carbonaceous waste feedstocks. Three examples are described.
Indirectly irradiated packed-bed reactor
The solar reactor configuration is shown schematically in Fig. 4.10 It is specifically designed for beam-down incident solar radiation as obtained through a Cassegrain optical configuration that makes use of a hyperbolic reflector at the top of a solar tower to redirect sunlight collected by a heliostat field to a receiver located at ground level.42 It consists of two cavities in series. The upper cavity functions as the solar absorber and contains a windowed aperture to let in concentrated solar radiation. The lower cavity functions as the reaction chamber and contains the packed bed on top of the steam injector. An emitter plate separates the two cavities. Its main purpose is to eliminate contact between the quartz window and the reactants/products, preventing deposition of particles or condensable gases and ensuring a clean window during operation. The window increases reflection losses of incident solar radiation, but due to its spectrally selective nature decreases IR radiation losses compared to a windowless cavity.43 A CPC is incorporated at the reactor's aperture to further augment the incident solar flux before passing it through the quartz window into the upper cavity. Thus, the emitter plate is directly irradiated and acts as solar absorber and radiant emitter to the lower cavity. The upper cavity also serves as a thermal shock absorber; a desirable property given the intermittent nature of concentrated solar radiation. The reactor is operated in batch mode, with the packed bed shrinking as gasification progresses. An 8 kW reactor prototype was fabricated with an upper cavity containing a 6.5 cm diameter aperture and a 14.3 cm diameter, 16 cm height lower cylindrical cavity. The 6 mm thick emitter plate was made of SiC-coated graphite fibers so as to achieve high thermal conductivity while resisting the reducing atmosphere. This reactor concept was designed along the guidelines for “two-cavity” type solar reactors44 previously applied to the carbothermal reduction of ZnO45 and the detoxification of solid wastes.46
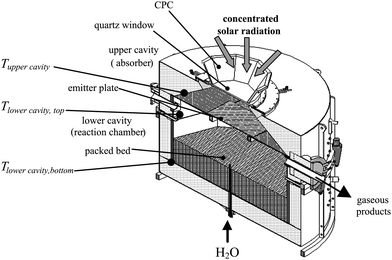 |
| | Fig. 4 Scheme of the indirectly irradiated packed-bed solar reactor configuration, featuring two cavities separated by an emitter plate, with the upper one serving as the radiative absorber and the lower one containing the reacting packed bed that shrinks as the reaction progresses. | |
The reactor concept of Fig. 4 was applied to the gasification of charcoal, bituminous coal, and carbonaceous wastes such as scrap tire chips and powders, sewage and industrial sludge and fluff.10 These carbonaceous wastes were characterized by volatile contents up to 80 wt%, ash contents up to 40 wt% and high heterogeneity. Experimentation was carried out at PSI's High Flux Solar Simulator47 with solar concentrations up to 2650 suns. Fig. 5 shows the temperatures of the upper cavity, emitter plate, and bottom of the lower cavity, the radiative power input through the reactor's aperture as measured optically by a calibrated CCD camera, and the evolved gases as measured by gas chromatography for a representative solar experimental run gasifying scrap tire powder. The temperatures at the top of the reactor responded rapidly to the increase in radiation while poor thermal conductivity of the packed bed strongly impeded the temperature rise at the bottom of the bed. Within phase 1, pyrolysis took place in the packed bed as indicated by the strong evolution of CH4 until roughly 50 minutes when the entire bed exceeded 1000 K. In phase 2, uniquely gasification took place at temperatures up to 1525 K with the evolution of syngas with a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio of about 1.33 and a CO2
CO ratio of about 1.33 and a CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio of about 0.2. Near the end of the run, in phase 3, the temperatures slowly rose while syngas production fell steadily due to the depletion of feedstock and a decrease in the endothermic heat sink. Variations in steam flow produced the expected rise in both H2 and CO2. The upgrade factor, the solar-to-fuel energy conversion efficiency, and other performance indicators of the solar reactor and the process are shown in Table 1.
CO ratio of about 0.2. Near the end of the run, in phase 3, the temperatures slowly rose while syngas production fell steadily due to the depletion of feedstock and a decrease in the endothermic heat sink. Variations in steam flow produced the expected rise in both H2 and CO2. The upgrade factor, the solar-to-fuel energy conversion efficiency, and other performance indicators of the solar reactor and the process are shown in Table 1.
Table 1 Performance indicators of the solar reactor for the steam-gasification of carbonaceous feedstocks in an indirectly irradiated packed-bed reactor (Fig. 4)
| Feedstock |
Industrial sludge |
Sewage sludge |
Scrap tire powder |
Fluff |
S. African coal |
Beech charcoal |
|
U (—) |
1.07 |
1.16 |
0.83 |
0.69 |
1.25 |
1.30 |
|
η
solar-to-fuel (%) |
28 |
18 |
17 |
16 |
23 |
29 |
| Packed-bed mass reduction/kg |
0.423 |
0.488 |
0.263 |
0.629 |
0.378 |
0.291 |
| Average bed shrink rate/cm h−1 |
4.1 |
2.6 |
2.2 |
4.1 |
1.5 |
2.8 |
| Packed-bed top surface temperature/K |
1490 |
1423 |
1470 |
1423 |
1470 |
1490 |
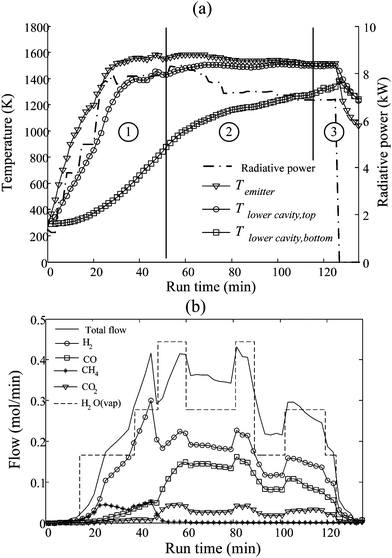 |
| | Fig. 5 Experimentally measured (a) temperatures in the solar reactor, and radiative power input through the reactor's aperture and (b) molar flow rates of evolved gases and steam supplied for the solar-driven gasification of scrap tire powder using an indirectly irradiated packed-bed reactor (Fig. 4). | |
Directly irradiated vortex-flow reactor
The solar reactor configuration is shown schematically in Fig. 6.48–51 It consists of a cylindrical cavity-receiver for efficiently capturing concentrated solar radiation entering through a windowed aperture. The aperture is equipped with a diverging frustum for mounting the window where the radiation intensity is about 10 times lower and dust deposition is unlikely to occur. The fused quartz window is 3 mm thick and mounted in a water-cooled copper ring which also serves as a shield for spilled radiation. The frustum is oil-cooled and kept in the range 393–453 K to protect it from radiation spillage and prevent steam condensation. The window is actively cooled and kept clear from particles by means of an aerodynamic protection curtain created by combined tangential and radial flow nozzles. A slurry of carbonaceous particles and water is injected through an inlet port on the cavity top at a controlled rate. Inside the cavity, the slurry forms a vortex flow that progresses towards the rear along a helical path. With this arrangement, the particles are directly exposed to the high-flux solar irradiation, providing efficient heat transfer directly to the reaction site. Energy absorbed by the reactants is used to evaporate and superheat the water, raise the reactants' temperature to above 1300 K, and drive the gasification reaction. This reactor concept has been applied successfully for combined solar ZnO-reduction and CH4-reforming52 and for the solar thermal cracking of CH4 with simultaneous production of H2 and carbon black.53 A 5 kW prototype was fabricated with a 210 mm length, 120 mm inside diameter cylindrical cavity-receiver made of Inconel-601, lined with Al2O3, and insulated with Al2O3/ZrO2 ceramic foam.48
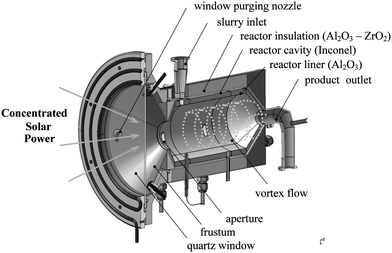 |
| | Fig. 6 Scheme of the directly irradiated vortex-flow solar reactor configuration, featuring a helical flow of carbonaceous particles and steam confined to a cavity-receiver and directly exposed to concentrated solar radiation. | |
Experimental runs were carried out at PSI's solar furnace.54 Three feedstocks were examined: dry powder petcoke, a water–petcoke slurry, and liquefied vacuum residue. For a nominal reactor temperature of 1500 K, a water–petcoke molar ratio of 4.8, and a residence time of 2.4 s, the degree of petcoke conversion was 87%. Typical syngas composition produced was 62% H2, 25% CO, 12% CO2, and 1% CH4. The reactor performance indicators were U = 1.2 and ηsolar-to-fuel = 26%. Heat losses were principally due to attenuation by the window and re-radiation through the aperture (∼16% of solar power input), and conduction through the reactor walls (∼67% of solar power input). Temperatures and gas compositions for a representative solar run are shown in Fig. 7. In this run, the reactor was first heated to above 1600 K under an Ar flow. Thereafter, reactants were continuously introduced during an interval of 14 minutes at a mass flow rate of 2.9 g min−1 of slurry with (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C)slurry = 2. Additionally, 4 g min−1 of H2O were injected to protect the window, corresponding to (H2O
C)slurry = 2. Additionally, 4 g min−1 of H2O were injected to protect the window, corresponding to (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C)T = 5.83. Main product gases were H2, CO, and CO2. Relatively small amounts of CH4 were derived from the pyrolysis of petcoke occurring immediately after exposure to the high-flux irradiation as a result of slurry heating rates exceeding 500 K s−1. Average values under approximate steady-state conditions, in the interval indicated by vertical dashed bars of Fig. 7, were: Treactor = 1601 K, ṅH2 = 0.05 mol min−1, ṅCO = 0.02 mol min−1, ṅCO2 = 0.01 mol min−1, and ṅCH4 = 0.001 mol min−1. H2S concentration reached up to 0.05%; its removal may be accomplished downstream, for example by gas scrubbing. Particle deposition or residual ash was not observed inside the reactor cavity. Thermogravimetric studies revealed a residuum of only 1.1 wt% after completion of the gasification reaction.23
C)T = 5.83. Main product gases were H2, CO, and CO2. Relatively small amounts of CH4 were derived from the pyrolysis of petcoke occurring immediately after exposure to the high-flux irradiation as a result of slurry heating rates exceeding 500 K s−1. Average values under approximate steady-state conditions, in the interval indicated by vertical dashed bars of Fig. 7, were: Treactor = 1601 K, ṅH2 = 0.05 mol min−1, ṅCO = 0.02 mol min−1, ṅCO2 = 0.01 mol min−1, and ṅCH4 = 0.001 mol min−1. H2S concentration reached up to 0.05%; its removal may be accomplished downstream, for example by gas scrubbing. Particle deposition or residual ash was not observed inside the reactor cavity. Thermogravimetric studies revealed a residuum of only 1.1 wt% after completion of the gasification reaction.23
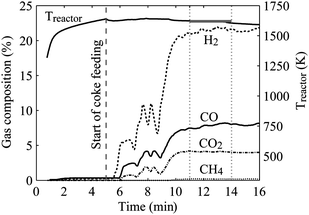 |
| | Fig. 7 Reactor temperature and product gas composition during a representative solar experimental run with petcoke–water slurry using a directly irradiated vortex-flow solar reactor (Fig. 6). Solar power input = 3.7 kW, mass flow rate of petcoke = 0.79 g min−1, molar slurry stoichiometry H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = 2. C = 2. | |
Indirectly irradiated entrained-flow reactor
The solar reactor configuration is shown schematically in Fig. 8. It consists of a cylindrical cavity-receiver with a windowless aperture containing an array of tubular absorbers, through which a continuous two-phase flow of water vapor laden with carbonaceous particles reacts to form syngas. A CPC is incorporated at the aperture to further augment the incident solar flux intensity, obtain a more uniform radiative distribution inside the cavity, and minimize re-radiation losses through a smaller aperture. Two small-scale solar reactor prototypes were fabricated:55,56 (1) a 5 cm diameter cylindrical cavity-receiver, made of 10 wt% YO2-stabilized ZrO2 lined with Al2O3 insulation, containing a single 2.5 cm diameter SiC concentric tubular absorber; and (2) a 18 cm diameter cylindrical cavity-receiver with specular reflective inner surfaces containing five 2.54 cm diameter tubular absorbers made of Al2O3 or Ni alloy. In both reactors, a trough CPC was incorporated at the rectangular windowless aperture. For the single-tube solar reactor,55 7.2 µm particles of beech charcoal were used as biomass feedstock. Fig. 9 shows the concentrated radiative power input, absorber temperature, and product gas composition during a representative experimental run with steam and charcoal feeding rates of 0.79 and 0.36 g min−1, respectively. The radiative power input varied in the range 0.8–1.6 kW, resulting in absorber temperatures ranging from 1100 to 1500 K. A maximum carbon conversion of 26% was achieved at 1425 K with a residence time of 0.08 s. Main product gases were H2, CO and CO2 with H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratios of 3 and CO2
CO ratios of 3 and CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratios of 1 due to the overstoichiometric water supply. Relatively small amount of CH4 was detected, most likely produced from pyrolysis reactions. For the given charcoal, steam, and Ar flow rates, a reaction zone length of 1.43 m would be required to reach complete carbon conversion after a 0.62 s residence time at an absorber temperature of 1600 K. For the multiple-tube solar reactor,56 150–300 µm particles of cellulose, lignin, and grass were used as biomass feedstock. Overall devolatilization of 98% and chemical conversion up to 58% were obtained at above 1400 K. Condensable tars were found at below 1273 K, but their formation decreased with temperature and was eliminated at above 1573 K.
CO ratios of 1 due to the overstoichiometric water supply. Relatively small amount of CH4 was detected, most likely produced from pyrolysis reactions. For the given charcoal, steam, and Ar flow rates, a reaction zone length of 1.43 m would be required to reach complete carbon conversion after a 0.62 s residence time at an absorber temperature of 1600 K. For the multiple-tube solar reactor,56 150–300 µm particles of cellulose, lignin, and grass were used as biomass feedstock. Overall devolatilization of 98% and chemical conversion up to 58% were obtained at above 1400 K. Condensable tars were found at below 1273 K, but their formation decreased with temperature and was eliminated at above 1573 K.
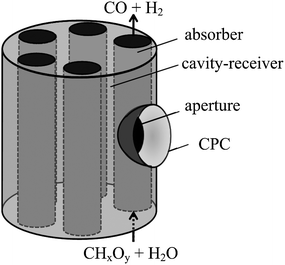 |
| | Fig. 8 Scheme of the indirectly irradiated entrained-flow solar reactor configuration, featuring a cylindrical cavity-receiver containing an array of tubular absorbers through which a continuous flow of water vapor laden with carbonaceous particles reacts to form syngas. | |
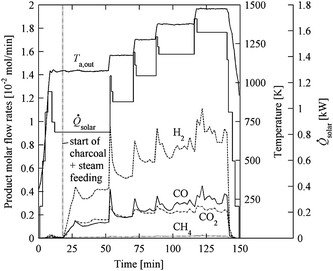 |
| | Fig. 9 Radiative power input, ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) solar, outer absorber temperature, Ta,out, and product gas composition during a representative experimental run using a indirectly irradiated entrained-flow solar reactor (Fig. 8) with a single tubular absorber. Steam and charcoal feeding rates: 0.79 and 0.36 g min−1, respectively. solar, outer absorber temperature, Ta,out, and product gas composition during a representative experimental run using a indirectly irradiated entrained-flow solar reactor (Fig. 8) with a single tubular absorber. Steam and charcoal feeding rates: 0.79 and 0.36 g min−1, respectively. | |
Of the three solar reactor concepts, the one based on the packed bed is the most flexible in handling and processing heterogeneous feedstocks with varying compositions and particle sizes (typically 0.1–10 mm). Because of long residence times, it can also tolerate lower reactivity feedstocks.27 However, its energy conversion efficiency is constrained by the rate of heat and mass transfer.10,22 In contrast, the solar reactors based on the entrained flow exhibit more efficient transport properties, but at the expense of being sensitive to particle sizes57 (typically <10 µm). Because of the short residence times, they are most suited to high reactivity feedstocks. The directly irradiated concept bypasses the limitations imposed by conductive heat transfer through ceramic walls and, consequently, promises high energy conversion efficiencies; however, it introduces a critical quartz window. The indirect-irradiated concept is a more technically feasible approach, but with an associated energy penalty.
Recently, pilot-scale solar gasification plants have been commissioned in solar towers. Holcim (Switzerland), in collaboration with PSI and ETH Zurich, has built a 260 kW solar gasifier based on the indirectly irradiated packed-bed solar reactor concept (Fig. 4), which is designed for the gasification of carbonaceous waste feedstocks. The 300 kW pilot version of the direct-irradiation vortex-flow reactor (Fig. 6) has been installed by the ETH Zürich, PDVSA (Venezuela), and CIEMAT (Spain) for the gasification of petcoke.57 Sundrop Fuels (USA), in collaboration with the University of Colorado, has constructed a 1 MW solar tower pilot plant with a solar biomass gasifier based on the indirectly irradiated entrained-flow reactor concept (Fig. 8).58 Ultimately, successful market entry of solar gasification technology will depend on the dominant market price of solid feedstocks and fossil fuels, as well as credits for pollution abatement and CO2 mitigation.
Solar reactor modeling
The modeling of solar gasification reactors, where the chemical species and their physical properties vary with time as the reaction progresses, involves solving the unsteady mass and energy conservation equations for a two-phase reacting media coupling radiative, conductive, and convective heat transfer with the reaction kinetics. Fig. 10 depicts the modeling schematics of the three solar reactor concepts, namely: (a) indirectly irradiated packed-bed (Fig. 4); (b) directly irradiated vortex-flow (Fig. 6), and (c) indirectly irradiated entrained flow (Fig. 8). The principal modes of heat transfer are indicated.
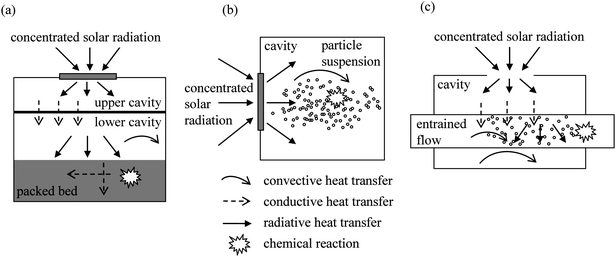 |
| | Fig. 10 Modeling schematics for the three solar reactor concepts: (a) indirectly irradiated packed-bed; (b) directly irradiated vortex-flow, and (c) indirectly irradiated entrained flow. | |
The indirectly irradiated packed-bed solar reactor, Fig. 10a, was modeled by considering radiative exchange in an enclosure and quasi-1D transient heat transfer in the reacting packed bed and cavity walls.22 Validation was accomplished in terms of bed temperatures, reacted mass, and bed shrink rates by comparing numerically calculated values with experimental results obtained from tests of the steam-gasification of beech charcoal in an 8 kW prototype solar reactor. Above 1300 K, radiative transfer was the predominant mode of heat transport within the bed, producing a seven-fold increase in the effective thermal conductivity. Conditions were typical of an ablation regime, characterized by the heat transfer to the depth of the bed being the reaction rate-controlling mechanism. The directly irradiated vortex-flow solar reactor, Fig. 10b, was modeled by means of a two-phase heat and mass transfer formulation for poly-disperse suspensions of reacting particles, and solved by advanced Monte Carlo (MC) and Finite Volume (FV) techniques with smoothing and underrelaxation.51,59 Validation was accomplished by comparing the numerically calculated temperatures, product compositions, and chemical conversions with the experimentally measured values obtained from testing a 5 kW solar reactor prototype in a high-flux solar furnace. Heating rates of 105 K s−1 were obtained as a result of the efficient radiative heat transfer. Transient radiative heat transfer was examined for a non-isothermal, non-gray, absorbing, emitting, and Mie-scattering suspension of coal particles undergoing shrinking by endothermic gasification.60,61 A numerical model that incorporates parallel filtered collision-based MC, FV, and explicit Euler time integration schemes was formulated for solving the unsteady energy equation that couples the radiative heat flux with the chemical kinetics. It was found that radiation in the visible and near IR spectrum incident on a cloud of coal particles greater than 2.5 µm is more likely to be forward-scattered than absorbed, but the opposite is true as the particles shrink below 1.3 µm. The medium becomes optically thinner as the particles shrink and this effect is more pronounced for smaller initial coal particles because these offer higher volume fractions to particle diameter ratios and, consequently, attain higher temperatures, reaction rates, and shrinking rates. A heat transfer numerical model was developed and experimentally validated for the steam-gasification of coal using a fluidized bed contained in a quartz tubular reactor that was directly exposed to concentrated thermal radiation.62 At above 1450 K, the gas composition consisted of a nearly equimolar mixture of H2 and CO, with less than 5% of CO2. Heat was transferred to the particles predominantly by thermal radiation and to the gas by particle–gas convection, since radiation absorption by particles was three orders of magnitude higher than that by the gas phase. The indirectly irradiated entrained-flow solar reactor, Fig. 10c, was modeled using MC and radiosity methods to determine the radiation distribution within the cavity,63,64 which in turn was coupled to 2D conductive heat transfer through the reactor tube which drove convective and radiative heat transfer to the entrained reactive flow of shrinking particles.64
The 3D digital geometrical representation of a packed bed containing porous carbonaceous materials was obtained by computer tomography and used in direct pore-level numerical simulations to characterize its morphology (porosity, specific surface, particle size distribution, and representative elementary volume) and determine its effective radiative transfer properties (extinction coefficient, scattering phase function, and scattering albedo) as a function of the reaction extent.65 These effective transport properties can be then incorporated in continuum models of the reacting packed bed.
Summary and conclusion
The thermodynamic analysis indicates the potential of converting carbonaceous feedstocks via thermochemical steam-gasification into syngas with an upgraded calorific value over that of the feedstock by up to 33%. Three prototype solar reactors based on the indirectly irradiated packed-bed, directly irradiated vortex-flow, and indirectly irradiated entrained-flow concepts were experimentally demonstrated, yielding high carbon conversions and reasonable solar-to-fuel energy conversion efficiencies. The quality of the syngas produced was high, especially in terms of the low CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO molar ratios, as no syngas contamination by combustion byproducts occurred. Even during gasification of waste materials and biomass feedstocks with high volatile contents, the temperatures achieved in the reactors were capable of breaking down the intermediate tars and pyrolysis products. Heat transfer models indicate that scaling-up to MW power levels should improve energy conversion efficiencies due to favorable volume-to-surface ratios of the cavity-receiver and optimal matching of heat transfer rates to reaction rates. The solar-driven process promises to achieve economic competitiveness vis-à-vis conventional autothermal gasification, mainly due to lower feedstock consumption and the elimination of the energy-intensive oxygen separation unit. Further R&D of the solar reactor technology is warranted and the first generation of industrial pilot plants at the solar power level of 0.5 MW is demonstrated.
CO molar ratios, as no syngas contamination by combustion byproducts occurred. Even during gasification of waste materials and biomass feedstocks with high volatile contents, the temperatures achieved in the reactors were capable of breaking down the intermediate tars and pyrolysis products. Heat transfer models indicate that scaling-up to MW power levels should improve energy conversion efficiencies due to favorable volume-to-surface ratios of the cavity-receiver and optimal matching of heat transfer rates to reaction rates. The solar-driven process promises to achieve economic competitiveness vis-à-vis conventional autothermal gasification, mainly due to lower feedstock consumption and the elimination of the energy-intensive oxygen separation unit. Further R&D of the solar reactor technology is warranted and the first generation of industrial pilot plants at the solar power level of 0.5 MW is demonstrated.
Nomenclature
|
C
| solar flux concentration ratio |
|
D
| diameter |
|
E
a
| apparent activation energy |
|
I
| direct normal solar irradiation |
|
k
| rate constant |
|
k
o
| frequency factor |
|
LHV
| lower heating value |
|
m
| mass |
|
n
| number of moles |
|
p
| pressure |
|
Q
| thermal energy |
|
r
| reaction rate, radius |
|
R
u
| universal gas constant |
|
T
| temperature |
|
t
| time |
|
U
| upgrade factor |
|
X
| conversion |
|
x
| mass fraction |
|
α
eff
| effective absorptance |
|
ε
eff
| effective emittance |
| ΔH | enthalpy change |
|
η
| efficiency |
|
ξ
| particle effectiveness |
|
σ
| Stefan–Boltzmann constant |
References
-
C. Higman and M. van der Burgt, Gasification, Gulf Professional Publishing, 2008 Search PubMed.
- I. Wender, Fuel Process. Technol., 1996, 48, 189–297 CrossRef CAS.
- M. Höök and K. Aleklett, Int. J. Energy Res., 2010, 34, 848–864 CAS.
- P. von Zedtwitz and A. Steinfeld, Energy, 2003, 28, 441–456 CrossRef CAS.
- P. von Zedtwitz, J. Petrasch, D. Trommer and A. Steinfeld, Sol. Energy, 2006, 80, 1333–1337 CrossRef CAS.
-
A. Steinfeld and R. Palumbo, in Encyclopedia of Physical Science and Technology, ed. R. A. Meyers, Academic Press, 2001, vol. 15, pp. 237–256 Search PubMed.
- P. D. Filippis, C. Borgianni, M. Paolucci and R. Pochetti, Waste Manage., 2004, 24, 633–639 CrossRef.
- M. Morris and L. Waldheim, Waste Manage., 1998, 18, 557–564 CrossRef CAS.
- T. Malkow, Waste Manage., 2004, 24, 53–79 CrossRef CAS.
- N. Piatkowski, C. Wieckert and A. Steinfeld, Fuel Process. Technol., 2009, 90, 360–366 CrossRef CAS.
-
K. H. Van Heek, in Carbon and Coal Gasification, ed. J. L. Figuieiredo, NATO ASI Series, 1986, pp. 383–411 Search PubMed.
- S. Koppatz, C. Pfeiler, R. Rauch, H. Hofbauer, T. Marquard-Moellenstedt and M. Specht, Fuel Process. Technol., 2009, 90, 914–921 CrossRef CAS.
- P. R. Solomon, M. A. Serio and E. R. Suuberg, Prog. Energy Combust. Sci., 1992, 18, 133–220 CrossRef CAS.
- V. Cozzani, L. Petarca and L. Tognotti, Fuel, 1995, 74, 903–912 CrossRef CAS.
- P. T. Williams, S. Besler and D. T. Taylor, Fuel, 1990, 69, 1474–1482 CrossRef CAS.
- F. Mermoud, S. Salvador, L. Van de Steene and F. Golfier, Fuel, 2006, 85, 1473–1482 CrossRef CAS.
- T. S. Pather and W. A. Al-Malry, J. Anal. Appl. Pyrolysis, 1996, 37, 83–94 CrossRef CAS.
- D. W. Gregg, W. R. Aiman, H. H. Otsuki and C. B. Thorsness, Sol. Energy, 1980, 24, 313–321 CrossRef CAS.
- D. W. Gregg, R. W. Taylor, J. H. Campbell, J. R. Taylor and A. Cotton, Sol. Energy, 1980, 25, 353–364 CrossRef CAS.
- J. Lédé, Sol. Energy, 1998, 65, 3–13.
- W. Beattie, R. Berjoan and J. P. Coutures, Sol. Energy, 1983, 31, 137–143 CrossRef CAS.
- N. Piatkowski and A. Steinfeld, Energy Fuels, 2008, 22, 2043–2052 CrossRef CAS.
- D. Trommer and A. Steinfeld, Energy Fuels, 2006, 20, 1250–1258 CrossRef CAS.
- D. Trommer, F. Noembrini, M. Fasciana, D. Rodriguez, A. Morales, M. Romero and A. Steinfeld, Int. J. Hydrogen Energy, 2005, 30, 605–618 CrossRef CAS.
- A. Z'Graggen and A. Steinfeld, Int. J. Heat Mass Transfer, 2009, 52, 385–395 CrossRef CAS.
- N. Piatkowski and A. Steinfeld, Fuel, 2010, 89, 1133–1140 CrossRef CAS.
- A.-G. Collot, Int. J. Coal Geol., 2006, 65, 191–212 CAS.
- H. Jüntgen, Fuel, 1983, 62, 234–238 CrossRef.
-
P. L. Walker, in Fundamentals of Thermochemical Biomass Conversion, ed. R. P. Overend, T. A. Milne and L. K. Mudge, Elsevier Applied Science, 1985, pp. 485–509 Search PubMed.
- A. Steinfeld and M. Schubnell, Sol. Energy, 1993, 50, 19–25 CrossRef CAS.
-
W. T. Welford and R. Winston, High Collection Nonimaging Optics, Academic Press, San Diego, 1989 Search PubMed.
- A. Kribus, P. Doron, R. Rubin, R. Reuven, E. Taragan, S. Duchan and J. Karni, J. Sol. Energy Eng., 2001, 123, 10–17 CrossRef CAS.
- S. Möller, D. Kaucic and C. Sattler, J. Sol. Energy Eng., 2006, 128, 16–23 CrossRef CAS.
- M. Flechsenhar and C. Sasse, Energy, 1995, 20, 803–810 CrossRef CAS.
- R. W. Taylor, R. Berjoan and J. P. Coutures, Sol. Energy, 1983, 30, 513–525 CrossRef CAS.
- T. Osinga, G. Olalde and A. Steinfeld, Ind. Eng. Chem. Res., 2004, 43, 7981–7988 CrossRef CAS.
- G. Ingle, M. Levy and J. Gordon, Sol. Energy Mater., 1991, 24, 478–489 CrossRef.
- J. P. Murray and E. A. Fletcher, Energy, 1994, 19, 1083–1098 CrossRef CAS.
- R. Müller, P. Von Zedtwitz, A. Wokaun and A. Steinfeld, Chem. Eng. Sci., 2003, 58, 5111–5119 CrossRef CAS.
- T. Kodama, T. Kondoh, T. Tamagawa, A. Funatoh, K.-I. Shimizu and Y. Kitayama, Energy Fuels, 2003, 16, 1264–1270.
- P. von Zedtwitz and A. Steinfeld, Ind. Eng. Chem. Res., 2008, 44, 3852–3861.
- A. Yogev, A. Kribus, M. Epstein and A. Kogan, Int. J. Hydrogen Energy, 1997, 23, 239–245.
- A. Z'Graggen and A. Steinfeld, J. Sol. Energy Eng., 2004, 126, 819–822 CrossRef CAS.
- C. Wieckert, A. Meier and A. Steinfeld, J. Sol. Energy Eng., 2003, 125, 121–123.
- C. Wieckert, U. Frommherz, S. Kräupl, E. Guillot, G. Olalde and M. Epstein, J. Sol. Energy Eng., 2007, 129, 190–196 CrossRef CAS.
- B. Schaffner, A. Meier, D. Wuillemin, W. Hoffelner and A. Steinfeld, Environ. Sci. Technol., 2003, 37, 165–170 CrossRef CAS.
- J. Petrasch, P. Coray, A. Meier, M. Brack, P. Haeberling, D. Wuillemin and A. Steinfeld, J. Sol. Energy Eng., 2007, 129, 405–411 CrossRef CAS.
- A. Z'Graggen, P. Haueter, D. Trommer, M. Romero, J. C. de Jesus and A. Steinfeld, Int. J. Hydrogen Energy, 2006, 31, 797–811 CrossRef CAS.
- A. Z'Graggen, P. Haueter, G. Maag, A. Vidal, M. Romero and A. Steinfeld, Int. J. Hydrogen Energy, 2007, 32, 992–996 CrossRef CAS.
- A. Z'Graggen, P. Haueter, G. Maag, M. Romero and A. Steinfeld, Int. J. Hydrogen Energy, 2008, 33, 679–684 CrossRef CAS.
- A. Z'Graggen and A. Steinfeld, Chem. Eng. Process., 2008, 47, 655–662 CrossRef CAS.
- A. Steinfeld, M. Brack, A. Meier, A. Weidenkaff and D. Wuillemin, Energy, 1998, 23, 803–814 CrossRef CAS.
- G. Maag, G. Zanganeh and A. Steinfeld, Int. J. Hydrogen Energy, 2009, 34, 7676–7685 CrossRef CAS.
- P. Haueter, T. Seitz and A. Steinfeld, J. Sol. Energy Eng., 1999, 121, 77–80 CrossRef CAS.
- T. Melchior, C. Perkins, P. Lichty, A. W. Weimer and A. Steinfeld, Chem. Eng. Process., 2009, 48, 1279–1287 CrossRef CAS.
- P. Lichty, C. Perkins, B. Woodruff, C. Bingham and A. Weimer, J. Sol. Energy Eng., 2010, 132, 011012 CrossRef.
- A. Z'Graggen and A. Steinfeld, Int. J. Hydrogen Energy, 2008, 33, 5484–5492 CrossRef CAS.
- R. F. Service, Science, 2009, 326, 1474 CrossRef.
- A. Z'Graggen and A. Steinfeld, Int. J. Heat Mass Transfer, 2009, 52, 385–395 CrossRef CAS.
- W. Lipinski and A. Steinfeld, Heat Mass Transfer, 2005, 41, 1021–1032 Search PubMed.
- W. Lipiński, A. Z'Graggen and A. Steinfeld, Numer. Heat Transfer, Part B, 2005, 47, 443–457 Search PubMed.
- P. von Zedtwitz, W. Lipiński and A. Steinfeld, Chem. Eng. Sci., 2007, 62, 599–607 CrossRef CAS.
- T. Melchior, C. Perkins, A. W. Weimer and A. Steinfeld, Int. J. Therm. Sci., 2008, 47, 1496–1503 CrossRef CAS.
- T. Melchior and A. Steinfeld, J. Sol. Energy Eng., 2008, 130, 021013 CrossRef.
- S. Haussener, W. Lipinski, P. Wyss and A. Steinfeld, J. Heat Transfer, 2010, 132, 061201 CrossRef.
Footnote |
| † The solar flux concentration ratio is defined as the incident solar radiative power flux normalized by 1 kW m−2. It is often reported in units of “suns”. |
|
| This journal is © The Royal Society of Chemistry 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 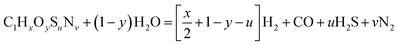
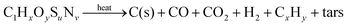


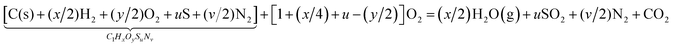

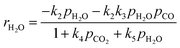
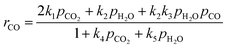
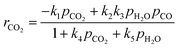
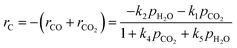
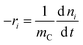
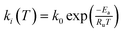
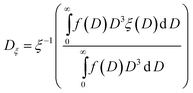
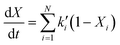
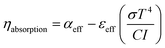

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 kJ kg−1 for anthracite. The energetic upgrade factor is defined as the ratio of the heating value of the syngas produced to that of the feedstock processed:
700 kJ kg−1 for anthracite. The energetic upgrade factor is defined as the ratio of the heating value of the syngas produced to that of the feedstock processed: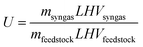

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio of about 1.33 and a CO2
CO ratio of about 1.33 and a CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio of about 0.2. Near the end of the run, in phase 3, the temperatures slowly rose while syngas production fell steadily due to the depletion of feedstock and a decrease in the endothermic heat sink. Variations in steam flow produced the expected rise in both H2 and CO2. The upgrade factor, the solar-to-fuel energy conversion efficiency, and other performance indicators of the solar reactor and the process are shown in Table 1.
CO ratio of about 0.2. Near the end of the run, in phase 3, the temperatures slowly rose while syngas production fell steadily due to the depletion of feedstock and a decrease in the endothermic heat sink. Variations in steam flow produced the expected rise in both H2 and CO2. The upgrade factor, the solar-to-fuel energy conversion efficiency, and other performance indicators of the solar reactor and the process are shown in Table 1.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C)slurry = 2. Additionally, 4 g min−1 of H2O were injected to protect the window, corresponding to (H2O
C)slurry = 2. Additionally, 4 g min−1 of H2O were injected to protect the window, corresponding to (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C)T = 5.83. Main product gases were H2, CO, and CO2. Relatively small amounts of CH4 were derived from the pyrolysis of petcoke occurring immediately after exposure to the high-flux irradiation as a result of slurry heating rates exceeding 500 K s−1. Average values under approximate steady-state conditions, in the interval indicated by vertical dashed bars of Fig. 7, were: Treactor = 1601 K, ṅH2 = 0.05 mol min−1, ṅCO = 0.02 mol min−1, ṅCO2 = 0.01 mol min−1, and ṅCH4 = 0.001 mol min−1. H2S concentration reached up to 0.05%; its removal may be accomplished downstream, for example by gas scrubbing. Particle deposition or residual ash was not observed inside the reactor cavity. Thermogravimetric studies revealed a residuum of only 1.1 wt% after completion of the gasification reaction.23
C)T = 5.83. Main product gases were H2, CO, and CO2. Relatively small amounts of CH4 were derived from the pyrolysis of petcoke occurring immediately after exposure to the high-flux irradiation as a result of slurry heating rates exceeding 500 K s−1. Average values under approximate steady-state conditions, in the interval indicated by vertical dashed bars of Fig. 7, were: Treactor = 1601 K, ṅH2 = 0.05 mol min−1, ṅCO = 0.02 mol min−1, ṅCO2 = 0.01 mol min−1, and ṅCH4 = 0.001 mol min−1. H2S concentration reached up to 0.05%; its removal may be accomplished downstream, for example by gas scrubbing. Particle deposition or residual ash was not observed inside the reactor cavity. Thermogravimetric studies revealed a residuum of only 1.1 wt% after completion of the gasification reaction.23
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = 2.
C = 2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratios of 3 and CO2
CO ratios of 3 and CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratios of 1 due to the overstoichiometric water supply. Relatively small amount of CH4 was detected, most likely produced from pyrolysis reactions. For the given charcoal, steam, and Ar flow rates, a reaction zone length of 1.43 m would be required to reach complete carbon conversion after a 0.62 s residence time at an absorber temperature of 1600 K. For the multiple-tube solar reactor,56 150–300 µm particles of cellulose, lignin, and grass were used as biomass feedstock. Overall devolatilization of 98% and chemical conversion up to 58% were obtained at above 1400 K. Condensable tars were found at below 1273 K, but their formation decreased with temperature and was eliminated at above 1573 K.
CO ratios of 1 due to the overstoichiometric water supply. Relatively small amount of CH4 was detected, most likely produced from pyrolysis reactions. For the given charcoal, steam, and Ar flow rates, a reaction zone length of 1.43 m would be required to reach complete carbon conversion after a 0.62 s residence time at an absorber temperature of 1600 K. For the multiple-tube solar reactor,56 150–300 µm particles of cellulose, lignin, and grass were used as biomass feedstock. Overall devolatilization of 98% and chemical conversion up to 58% were obtained at above 1400 K. Condensable tars were found at below 1273 K, but their formation decreased with temperature and was eliminated at above 1573 K.


![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) solar, outer absorber temperature, Ta,out, and product gas composition during a representative experimental run using a indirectly irradiated entrained-flow solar reactor (Fig. 8) with a single tubular absorber. Steam and charcoal feeding rates: 0.79 and 0.36 g min−1, respectively.
solar, outer absorber temperature, Ta,out, and product gas composition during a representative experimental run using a indirectly irradiated entrained-flow solar reactor (Fig. 8) with a single tubular absorber. Steam and charcoal feeding rates: 0.79 and 0.36 g min−1, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO molar ratios, as no syngas contamination by combustion byproducts occurred. Even during gasification of waste materials and biomass feedstocks with high volatile contents, the temperatures achieved in the reactors were capable of breaking down the intermediate tars and pyrolysis products. Heat transfer models indicate that scaling-up to MW power levels should improve energy conversion efficiencies due to favorable volume-to-surface ratios of the cavity-receiver and optimal matching of heat transfer rates to reaction rates. The solar-driven process promises to achieve economic competitiveness vis-à-vis conventional autothermal gasification, mainly due to lower feedstock consumption and the elimination of the energy-intensive oxygen separation unit. Further R&D of the solar reactor technology is warranted and the first generation of industrial pilot plants at the solar power level of 0.5 MW is demonstrated.
CO molar ratios, as no syngas contamination by combustion byproducts occurred. Even during gasification of waste materials and biomass feedstocks with high volatile contents, the temperatures achieved in the reactors were capable of breaking down the intermediate tars and pyrolysis products. Heat transfer models indicate that scaling-up to MW power levels should improve energy conversion efficiencies due to favorable volume-to-surface ratios of the cavity-receiver and optimal matching of heat transfer rates to reaction rates. The solar-driven process promises to achieve economic competitiveness vis-à-vis conventional autothermal gasification, mainly due to lower feedstock consumption and the elimination of the energy-intensive oxygen separation unit. Further R&D of the solar reactor technology is warranted and the first generation of industrial pilot plants at the solar power level of 0.5 MW is demonstrated.
