Transition metal induced magnetism in smaller fullerenes (Cn for n ≤ 36)
Isha
Garg
a,
Hitesh
Sharma
*b,
Neha
Kapila
a,
Keya
Dharamvir
a and
V. K.
Jindal
a
aDepartment of Physics, Center of Advanced Studies in Physics, Panjab University, Chandigarh, India 160014
bPhysics Division, D.E.P, Punjab Technical University, Jalandhar, 144601, India. E-mail: dr.hitesh.phys@gmail.com; Fax: 01822-662502
First published on 27th October 2010
Abstract
The magnetic properties of 3d transition metals (TM) encapsulated inside smaller fullerenes ranging from C20 to C36 have been investigated using spin polarized density functional theory. The TM impurities stabilize asymmetrically at an off-center position for n ≥ 28. The total magnetic moment (MM) of TM@Cn complexes are largely contributed by TMs and a small amount of MM of 0.12–0.50 μB is induced on the cage carbon atoms. The 3d TM atoms interact with C atoms of C20 and C28 cage ferromagnetically (FM) except for Ni@C28 which shows antiferromagnetic (AFM) interaction. The magnetic interactions change from FM to AFM in C32 cage for Ti, V, Cr and Mn. The MM gets quenched in Ni@Cn for n ≥ 32. The total MM of Mn@Cn does not show any change although the nature of magnetic interactions changes from FM to AFM at n = 32. Ti and V are the only TMs which show positive cohesive energy in all fullerenes considered. The smallest fullerene which can encapsulate all 3d TM are Cn for n ≥ 32, consistent with available experimental and theoretical results.
I. Introduction
Recent experimental results on magnetism in carbon based materials have renewed interest in carbon systems as possible new magnetic materials due to their technological advantages over conventional magnetic materials,1 though the origin of the magnetic ordering in the latter systems is still far from clear. The quest for carbon based ferromagnetism has occupied theoreticians for many years and its origin has been proposed to be due to the dislocations, vacancies and impurity atoms.2 To date, the focus has been to understand the magnetic properties of metallofullerenes larger than C603–5 due to their stability and larger volume available for encapsulation. Among the smaller fullerenes only C20 and C36 have been isolated so far. Lopez et al.6 have studied magnetic properties of carbon clusters, clusters inside fullerenes and graphitic nanoribbons. The entrapped atoms bring with them an array of useful physical properties with possible applications in electronic devices,7 organic solar cells,8 spin-based quantum computing9,10 and medicine,11 specifically contrast agents for magnetic resonance imaging (MRI) as well as for radiopharmaceutical candidates.12The recent works on the successful synthesis of some endohedral derivations of smaller fullerenes have acquired special significance. The smaller fullerenes violate the isolated pentagon rule and the fused pentagon structures in this class of fullerenes have a strong effect on their stability and electronic properties. Surprisingly, small endohedral metallofullerenes remains to be explored and their magnetic properties have not been investigated in spite of the successful production of many small fullerenes.13–16 There is a considerable range of carbon clusters, Cn for 20 < n ≤ 30, in which the crossover to fullerene structures have been reported. In the crossover region there are other structures which are energetically competitive such as planar or near-planar sheets and bowls, and monocyclic rings.17U@C28 films were synthesized in a cationic form by laser vaporization of a UO2/graphite mixture.17 Besides U@C28, the signals of U@C36, U@C44 and U@C58 were also observed in the mass spectrum with lower intensities. Thus, the internal uranium atom has apparently stabilized the fullerene cage and made U@C28 the end point of laser shrinking. The presence of Zr, Hf, Ti and Sc inside C28 cage has also been confirmed in the mass spectrum obtained from laser vaporization of graphite/metal-oxide composite discs.18 Subsequently, none of the experimental groups have been able to isolate the observed metallofullerenes. Following these experiments, many theoretical groups have performed a systematic investigation of a series of M@C28 (M = Mg, Al, Ca, Sc, Ti, Ge, Zr and Sn)19 and found that only Sc@C28 and Zr@C28 are thermodynamically stable in consequence of their large binding energies. Sun et al.20 studied the encapsulation of thirteen atoms from group IA to group VA (i.e. H, Li, Na, K, Be, Mg, Ca, B, Al, C, Si, N, P) and nine cations from group IA to group IIIA (i.e.H+, Li+, Na+, K+, Be2+, Mg2+, Ca2+, B3+ and Al3+) inside C32 cage. Recently, Chen et al.21 investigated the stabilities and molecular structures of noble gas atoms (i.e.He, Ne, Ar, and Kr) inside the C32 cage. Subsequently, inspired by the finding of U@C36, Kang22 gave a detailed calculation of the possible encapsulation of alkali metals (i.e.Li, Na, K) inside C36. However, so far there has been no study reported on the trapping of transition metals (TM) inside small fullerene cage structures.
In this paper, we present a systematic investigation of the electronic and magnetic properties of TM@Cn, n = 20, 28, 32, 36 where TM = Ti, V, Cr, Mn, Fe, Co, Ni and Cu using spin polarized density functional theory. Our results show that the magnetic properties of TM@Cn, apart from depending on 3d configuration and charge transfer from the TM atom to carbon cage, also depend on the specific geometric structure of the cage as well as location of the TM atom. The results highlight the possibility of designing magnetic devices if high spin configurations of 3d TMs can be preserved as the ground state or different spin manipulation.
II. Computational details
We have used the spin polarized density functional theory to study the magnetic properties of the TM@Cn complexes as implemented in the Spanish Initiative for Electronic Simulation with Thousands of Atoms (SIESTA) computational code.23 The electron exchange interactions were considered using generalized gradient approximation (GGA) that implements Perdew, Zunger and Ernzerhof (PBE) exchange–correlation.24 The core electrons are replaced by non-local, norm-conserving pseudo potentials factorized in the Kleinman-Bylander form,25 whereas valence electrons are described using linear combination of numerical pseudo atomic orbitals of the Sankey-Niklewski type26 but generalized for multiple-ζ and polarization functions. In this work, we have used a split valence double-ζ polarized (DZP) basis set. We considered 3d24s2, 3d34s2, 3d54s1, 3d54s2, 3d64s2, 3d74s2, 3d84s2 and 3d104s1 electronic configurations for Ti, V, Cr, Mn, Fe, Co, Ni and Cu, respectively. The structures are obtained by minimization of the total energy using Hellmann-Feynman forces, including Pulay like corrections. Structural optimizations were performed using conjugate gradient algorithm until the residual forces in the optimization are smaller than 0.001 eV/Å. We have studied C60 based heterofullerenes27,28 and endohedral complexes29 with similar methodology and parameters as described above. This validates the applicability and accuracy of our calculations to investigate smaller carbon fullerene-based systems.The test calculations were performed on TM dimers and the calculated magnetic moments (MM) and bond lengths of all the clusters are tabulated in Table 1. Our results are in qualitative agreement with the existing experimental and theoretical results for Mn, Fe, Co, Ni and Cu.30–32 The accuracy of the DFT results for 3d TM are reported to be highly dependent upon the functional employed with pure methods such as BLYP and BP86 performing better than hybrid functionals. No functional gives results directly comparable for all 3d TM species.33 A choice of other functionals, such as BLYP or BP86, is likely to improve accuracy for some dimer results in qualitative terms but may not change the overall behavior of TM@Cn complexes.
III. Results and discussion
A. Structures and stabilities of TM@Cn complexes
The C20 cage with Ih symmetry (Fig. 1) is considered the starting cage configuration to investigate the effect of 3d TMs. The average diameter and bond length of C20 is found to be 4.14 Å and 1.47 Å which are in agreement with Malolepsza et al.34 The binding energy is 8.32 eV per atom for Ih symmetry which possesses a MM of 2 μB in agreement with ref. 35. However, there is a considerable disagreement among theoreticians regarding symmetry and magnetic state of C20. This may be due to the importance of accurate treatment of electron correlation36 in smaller fullerenes. Galli et al.37 used LDA and GGA to predict the C20 cage with D3d symmetry as the most stable Jahn–Teller distorted cage structure. Wang et al.38 using hybrid DFT predicted the C2h symmetry as the most stable structure. This may be explained on the basis that C20 with Ih symmetry may undergo Jahn–Teller distortions and its symmetry is reduced to lower groups. Lu et al.39 using tight binding model found that C20 undergoes a magnetic to nonmagnetic transition and nonmagnetic to magnetic transition for Ih and D3d symmetries, respectively.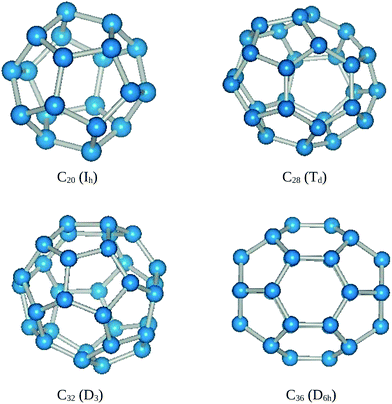 | ||
| Fig. 1 Optimized geometries of pure fullerenes along with their symmetries. | ||
The TMs prefer to stabilize at a central position in C20 and with their encapsulation, the variation in the C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of all the fullerene cages are tabulated in Table 2. The average C–C bond length in C20 is 1.47 Å and it increases to 1.48–1.54 Å in TM encapsulated complexes. The diameter of TM@C20 complexes increases from 4.21 to 4.27 Å from Ti to Cu. The binding energy per atom shows a maximum value of 8.2 eV for Ti@C20 which decreases with increasing atomic number of 3d TMs to 7.66 eV in Cu@C20. Further, the interaction between the fullerene cage and TMs along with the stabilities of TM@Cn complexes is described by evaluating their cohesive energies. We define the cohesive energy of TM@Cn complexes as follows:
C bond lengths of all the fullerene cages are tabulated in Table 2. The average C–C bond length in C20 is 1.47 Å and it increases to 1.48–1.54 Å in TM encapsulated complexes. The diameter of TM@C20 complexes increases from 4.21 to 4.27 Å from Ti to Cu. The binding energy per atom shows a maximum value of 8.2 eV for Ti@C20 which decreases with increasing atomic number of 3d TMs to 7.66 eV in Cu@C20. Further, the interaction between the fullerene cage and TMs along with the stabilities of TM@Cn complexes is described by evaluating their cohesive energies. We define the cohesive energy of TM@Cn complexes as follows:
| ΔE = ETotal(TM@Cn) − E(Cn) − E(TM) | (1) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths (in Å) for all fullerene cages
C bond lengths (in Å) for all fullerene cages
| TM | C20 | C28 | C32 | C36 | |||
|---|---|---|---|---|---|---|---|
| C–C | C–C | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–C | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–C | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
|
| Ti | 1.48–1.51 | 1.46–1.51 | 1.43 | 1.48–1.49 | 1.43 | 1.46–1.49 | 1.44 |
| V | 1.51–1.53 | 1.49–1.52 | 1.42–1.44 | 1.46–1.50 | 1.42–1.43 | 1.44–1.49 | 1.44 |
| Cr | 1.47–1.51 | 1.50–1.54 | 1.44 | 1.46–1.49 | 1.42 | 1.47–1.49 | 1.46 |
| Mn | 1.51–1.54 | 1.49–1.54 | 1.44 | 1.46–1.50 | 1.45 | 1.46–1.49 | 1.44–1.46 |
| Fe | 1.52–1.54 | 1.47–1.53 | 1.43 | 1.46–1.49 | 1.42–1.44 | 1.46–1.49 | 1.44–1.46 |
| Co | 1.51–1.53 | 1.46–1.53 | 1.44 | 1.47–1.48 | 1.42–1.45 | 1.45–1.49 | 1.44–1.45 |
| Ni | 1.51–1.54 | 1.47–1.53 | 1.43–1.44 | 1.46–1.51 | 1.42–1.44 | 1.46–1.50 | 1.45 |
| Cu | 1.50–1.54 | 1.47–1.52 | 1.44 | 1.46–1.50 | 1.42.1.44 | 1.46–1.50 | 1.43–1.45 |
| TM | TM@C20 | TM@C28 | TM@C32 | TM@C36 |
|---|---|---|---|---|
| Ti | 3.80 | 2.88 | 2.69 | 3.05 |
| V | 1.93 | 2.18 | 2.11 | 2.12 |
| Cr | −3.23 | −0.60 | −0.05 | 0.52 |
| Mn | −6.31 | 0.41 | 0.37 | 0.85 |
| Fe | −3.47 | 1.35 | 0.73 | 0.99 |
| Co | −4.19 | 0.27 | −0.54 | −0.26 |
| Ni | −4.75 | 0.54 | 0.25 | 0.55 |
| Cu | −7.52 | −0.59 | −0.08 | 0.21 |
From Table 3, it is clear that only Ti and V possess positive values for the C20 cage thereby suggesting the stabilities of these are likely to form complexes with C20.
C28
fullerene with Td symmetry and zero MM is found to be the most stable geometry compared to the other isomers considered. The TMs have a tendency to occupy off-center positions inside C28 and larger fullerenes as shown in Fig. 2. The average diameter of C28 comes out to be 4.88 Å with a binding energy per atom of 8.67 eV. The average C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of C28 are 1.45–1.47 Å and 1.42 Å whereas TM@C28 complexes show an increase to 1.49–1.54 Å and 1.44 Å, respectively. The average diameter shows a maximum value of 4.98 Å in Cr@C28. The structural behavior of Sc@C28 and Ti@C28, i.e. the distance of Sc and Ti from the nearest carbon cage atom, is 1.69 Å and 1.75 Å, respectively, in agreement with ref. 18. The binding energy per atom is higher for Sc@C28, Ti@C28 and V @C28, predicting their larger stability over their counterparts. ΔE for all TMs, except Cr and Cu, shows small positive values inside C28.
C bond lengths of C28 are 1.45–1.47 Å and 1.42 Å whereas TM@C28 complexes show an increase to 1.49–1.54 Å and 1.44 Å, respectively. The average diameter shows a maximum value of 4.98 Å in Cr@C28. The structural behavior of Sc@C28 and Ti@C28, i.e. the distance of Sc and Ti from the nearest carbon cage atom, is 1.69 Å and 1.75 Å, respectively, in agreement with ref. 18. The binding energy per atom is higher for Sc@C28, Ti@C28 and V @C28, predicting their larger stability over their counterparts. ΔE for all TMs, except Cr and Cu, shows small positive values inside C28.
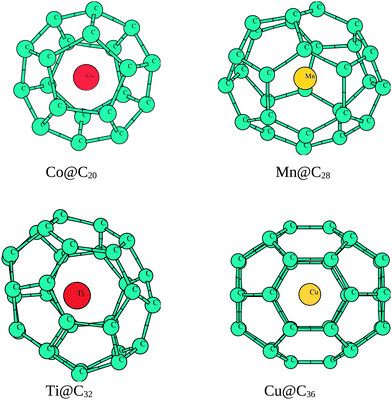 | ||
| Fig. 2 Optimized geometries of fullerenes doped with transition metals. | ||
C32 with D3h symmetry forms a stable cage with zero MM. C32 has an average diameter of 5.08 Å and the binding energy per atom is 8.83 eV with average C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of 1.47–1.49 Å. As a result of TM substitution inside C32 cage, the average diameter shows a slight increase with a maximum value of 5.16 Å for Co@C32. The average C–C and C
C bond lengths of 1.47–1.49 Å. As a result of TM substitution inside C32 cage, the average diameter shows a slight increase with a maximum value of 5.16 Å for Co@C32. The average C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of TM@C32 complexes lie in the range 1.46–1.51 Å (see Table 2). The binding energies show a similar pattern as that shown by C20 and C28, i.e. higher values of 8.65 eV and 8.63 eV for Ti and V respectively and decreasing value for other TMs. The cohesive energies tabulated in Table 3 shows very small negative cohesive energies for Cr, Co, and Cu which suggests their lower stability and that it may not be feasible to encapsulate them inside C32. All the other TMs show positive cohesive energies leading to the fact that they all form stable complexes with C32.
C bond lengths of TM@C32 complexes lie in the range 1.46–1.51 Å (see Table 2). The binding energies show a similar pattern as that shown by C20 and C28, i.e. higher values of 8.65 eV and 8.63 eV for Ti and V respectively and decreasing value for other TMs. The cohesive energies tabulated in Table 3 shows very small negative cohesive energies for Cr, Co, and Cu which suggests their lower stability and that it may not be feasible to encapsulate them inside C32. All the other TMs show positive cohesive energies leading to the fact that they all form stable complexes with C32.
C36 with D6h symmetry is found to be the most stable geometry with an average diameter of 5.30 Å and 8.89 eV binding energy per atom. The average C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths lies in the range 1.45–1.50 Å and 1.43–1.45 Å, respectively. The TM substitution does not change the diameter to a large extent, rather it remains nearly constant between 5.30–5.33 Å and the average bond lengths are the same for C–C, but C
C bond lengths lies in the range 1.45–1.50 Å and 1.43–1.45 Å, respectively. The TM substitution does not change the diameter to a large extent, rather it remains nearly constant between 5.30–5.33 Å and the average bond lengths are the same for C–C, but C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C changes to 1.44–1.46 Å. The binding energy shows the same trend as shown by other smaller fullerenes. The cohesive energies tabulated in Table 3 shows a positive value for all TMs except for Co which shows a negative value of −0.26 eV. Further, we can conclude that C36 is the smallest fullerene to encapsulate Cr and Cu.
C changes to 1.44–1.46 Å. The binding energy shows the same trend as shown by other smaller fullerenes. The cohesive energies tabulated in Table 3 shows a positive value for all TMs except for Co which shows a negative value of −0.26 eV. Further, we can conclude that C36 is the smallest fullerene to encapsulate Cr and Cu.
In order to examine the stability of 3d TMs at the surface position in small fullerenes, we performed structure optimization of the Cn−1TM for n = 32 and 36. The total energy calculations suggest TM@Cn is more stable than Cn−1TM complexes. The stability of Cn−1TM complexes increases with an increase in atomic number of TM, consistent with the pattern observed in TMC59 systems40 but different from the stability of TM@Cn complexes.
Furthermore, from the structural analysis of TM@Cn, we find that all the TMs prefer to place themselves at a central position for n = 20 and nearly off-center positions for n ≥ 28 within the cage by distorting the cage symmetry. The distortion in fullerene cages due to TM encapsulation is maximum for n = 20 and minimum for n = 36. The binding energy of TM@Cn decreases with increasing atomic number from Ti to Cu in all the fullerenes considered, although the rate of decrease falls with increasing diameter. The average bond lengths and diameters also show an increase due to TM encapsulation. The positive or negative ΔE values indicate the feasibility of formation of these endohedral complexes. Ti and V are the only two TMs which show positive values for all the fullerene cages which suggest a strong possibility for their formation experimentally. Only Cr and Cu show negative values for C28 and all the other TMs form stable complexes with C28. Similarly, in C32, Cr and Cu show small negative values which suggest that these complexes can be formed but with somewhat less stability. However, Co shows a comparatively higher negative value which indicates its unstable nature inside C32 cage. Further, in C36, except Co, the cohesive energies show positive values which suggest the stability of all TMs inside this cage.
B. Electronic and magnetic properties of TM@Cn
The electronic properties of TM@Cn complexes are investigated in terms of the HOMO (highest occupied molecular orbital)–LUMO (lowest unoccupied molecular orbital) gap as well as the electronic density of states (EDOS).The HOMO–LUMO gap for both spin up (↑) and spin down (↓) states as a function of 3d TMs with increasing atomic number is plotted in Fig. 3. The spin ↑ gap shows a sharp decrease from V to Cr and vice versa in the spin ↓ gap, with an oscillatory pattern thereafter in C20. For the TM@C28 complexes, the spin ↑ gap shows a sharp increase from Cr to Mn and is nearly constant thereafter, whereas the spin ↓ gap decreases sharply from Mn to Fe and shows an oscillatory pattern after that but decreases to 0.36 eV for Cu. For C32, the spin ↑ gap decreases from 1.41 eV in pure C32 to 0.68 eV in Fe@C32 and shows sharp increase from Fe to Co and then decrease for Cu. The spin ↓ gap shows a similar pattern as the spin ↑ gap but it increases sharply from Mn to Fe and then decreases for Co, with a further increase for Cu. In C36, the spin ↑ gap decreases from 0.83 eV for pure C36 to 0.41 eV for V@C36, then increases to 0.76 eV (Cr) and then gradual decreases to 0.73 eV (Cu). The spin ↓ gap shows a similar behavior as the spin ↑ gap with the only exception being Co which has a very small gap of 0.12 eV.
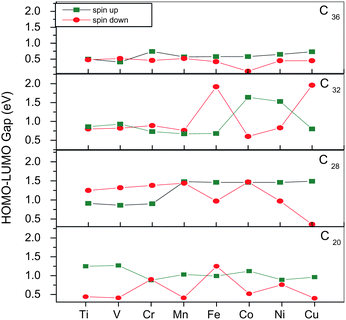 | ||
| Fig. 3 HOMO–LUMO gaps for spin up and spin down states for all TM@C20, C28, C32 and C36. | ||
The EDOS of TM@Cn complexes are plotted in Fig. 4(a) which shows a polarized EDOS for C20 at the Fermi level (Ef) even without encapsulating TMs. On encapsulation with Ti and V, the EDOS is modified significantly near Ef with the spin ↓ EDOS greater than the spin ↑ EDOS. The EDOS of C20 shows occupied states within the range −4.0 to −2.0 eV in contrast to Ti and V which shows unoccupied states. In the Cr@C20 complex, spin ↑ and spin ↓ EDOS are almost equal with 0.85 eV for the HOMO–LUMO gap.
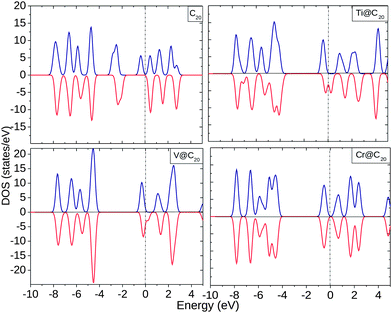 | ||
| Fig. 4 Electronic density of states (EDOS) for C20, Ti@C20, V@C20, and Cr@C20. The dotted line shows the position of the Fermi level (Ef). | ||
The Mulliken charge analysis shows an interesting pattern for the charge redistribution in TM@C20 complexes. Ti, V, and Cr donates ∼0.36–0.55 electrons to the C20 cage structure, Mn and Fe gain 0.12 electrons from nearby C atoms, whereas Co, Ni and Cu show no charge transfer. Apart from the external charge transfer in all the complexes, the internal transfer of electrons takes place from 4s to 3d and 4p orbitals significantly.
The EDOS for TM@C28 complexes are plotted in Fig. 5. EDOS for C28 is equal for both spin ↑ and spin ↓ electrons. However, with the encapsulation of TMs the EDOS show significant change at and below the Ef. Ti shows finite spin ↑ states at Ef and modified spin ↑ and ↓ EDOS up to −4.0 eV below Ef. V shows a similar behavior as Ti with the only difference being the finite spin ↑ EDOS near Ef. For Mn, there is an equal HOMO–LUMO gap for spin ↑ and spin ↓ electrons with unoccupied states at Ef. For Fe and Ni, the EDOS show a similar behavior at and near Ef with an equal HOMO–LUMO gap.
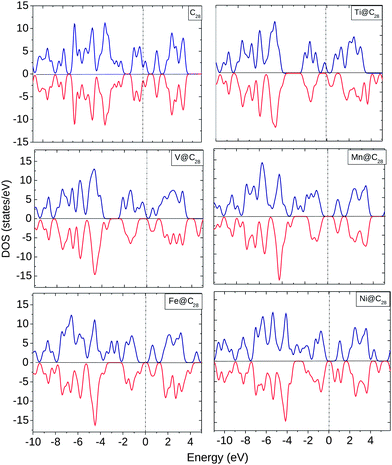 | ||
| Fig. 5 EDOS for C28, Ti@C28, V@C28, Mn@C28, Fe@C28, and Ni@C28. The dotted line shows the position of Ef. | ||
To further elucidate the origin of FM, the projected density of states (PDOS) for both Ti and Ni inside C28 cage are plotted in Fig. 6, as the former behaves as the acceptor and the latter behaves as the donor with respect to neighboring carbon atoms. Fig. 6(a) represents PDOS for Ti, which shows that the electronic states in the vicinity of Ef come mainly from up 3d states with empty down 3d states. In Ni, spin ↓ DOS are finite and gives significant contribution at and near Ef, whereas up 3d states show finite contribution within the region −3.0 to −1 eV. For both Ti and Ni, 4s and 4p states do not show any contribution near Ef, whereas all 3d up and 3d down components lie in its vicinity.
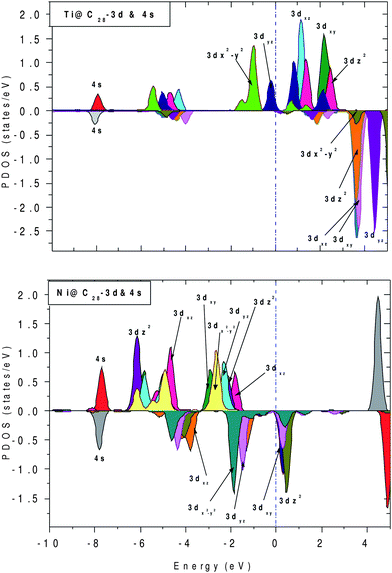 | ||
| Fig. 6 Projected density of states (PDOS) for Ti@C28 and Ni@C28 with their 4s and 3d contributions. The dotted line shows the position of Ef. | ||
For TM@C28 complexes, Ti gains ∼0.30 electrons from C28 cage and Ni loses ∼0.72 electrons to surrounding C atoms. The 4s orbital of Ni has lost 0.2 electrons to the 3d orbital, 0.7 electrons to the 4p orbital and 0.7 electrons to the C28 cage, with 0.32 electrons remaining in the 4s orbital. Therefore, there is an internal conversion as well as donation of electron that takes place from 4s.
For the C32 cage, the spin ↑ and spin ↓ EDOS are equal with unoccupied states at Ef. Ti shows an increased spin ↑ EDOS whereas V shows more contribution from spin ↓ EDOS, as shown in Fig. 7. At Ef, Mn and Fe show similar behavior and below Ef, up to −4.0 eV, there is a significant change in EDOS. For Ni, the complex shows half-metallic behavior with finite spin ↓ EDOS and very small spin ↑ EDOS near Ef. Inside the C32 cage, all the 3d TMs behave as donors by donating ∼0.11–0.86 electrons to the surrounding cage C atoms. Like all the other cages considered, the 4s orbital loses charge to the cage as well as undergoing internal conversion of electrons with 3d and 4p orbitals.
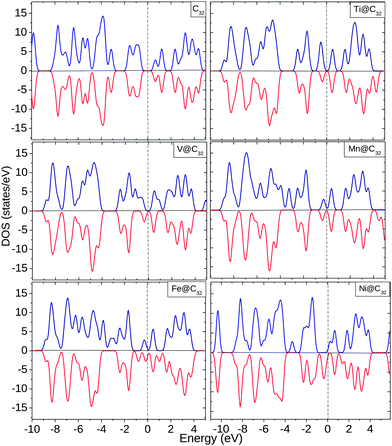 | ||
| Fig. 7 EDOS for C32, Ti@C32, V@C32, Mn@C32, Fe@C32 and Ni@C32. The dotted line shows the position of Ef. | ||
EDOS for TM@C36 complexes show a similar behavior as shown by TM@C32 complexes with a small change in the EDOS at the Ef which is depicted in the HOMO–LUMO gap (Fig. 3). The difference in the spin ↑ and spin ↓ EDOS for TM@Cn complexes is because of the presence of strong electronic polarization arising due to transfer of charges. The Mulliken charge analysis predicts that V, Cr and Cu inside the C36 cage act as donors by losing ∼0.4–0.76 electrons to the surrounding C atoms.
To study the evolution of magnetic properties of Cnfullerenes, we calculated the total MMs of TM@Cn complexes and the local magnetic moments (LMM) of TMs (see Fig. 8). The local MM at the 3d TM site along with the individual contributions of 3d, 4p and 4s orbitals are tabulated in Table 4. Due to the Jahn–Teller distortion and strong hybridization C20 with Ih symmetry has an intrinsic MM of 2 μB which is consistent with ref. 33 and in TM@C20 complexes, the MM varies from 2 μB for Ti@C20 to 5 μB in Cu@C20, whereas for Cr@C20, the MM gets quenched (Fig. 8). In TM@C20 complexes, the LMM is not fully localized at the TM site but also a significant amount is induced at the nearest neighboring C atoms. The magnetic interaction between TM impurities at the endo position and the surface C atoms is ferromagnetic (FM) in nature. 20–60% of the total MM is contributed by TM which is due to unpaired 3d electrons.
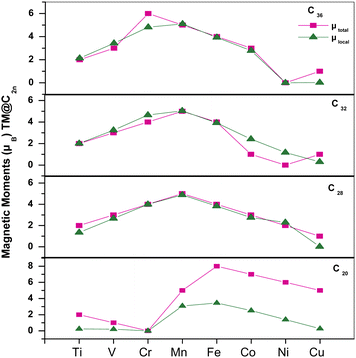 | ||
| Fig. 8 Total magnetic moments and local MMs at the TM site with respect to the 3d TMs for all fullerenes, i.e.C20, C28, C32 and C36. | ||
| TM | C20 | C28 | C32 | C36 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ TM | μ 3d | μ 4p | μ 4s | μ TM | μ 3d | μ 4p | μ 4s | μ TM | μ 3d | μ 4p | μ 4s | μ TM | μ 3d | μ 4p | μ 4s | |
| Ti | 0.24 | 0.18 | 0.04 | 0.02 | 1.36 | 1.33 | 0.01 | 0.01 | 2.00 | 1.99 | 0.05 | 0.03 | 2.13 | 2.03 | 0.06 | 0.04 |
| V | 0.20 | 0.17 | 0.02 | 0.01 | 2.66 | 2.60 | 0.03 | 0.01 | 3.24 | 3.08 | 0.09 | 0.06 | 3.43 | 3.38 | 0.10 | 0.08 |
| Cr | 0.00 | 0.00 | 0.00 | 0.00 | 3.99 | 3.88 | 0.04 | 0.05 | 4.65 | 4.43 | 0.12 | 0.09 | 4.82 | 4.60 | 0.12 | 0.09 |
| Mn | 3.08 | 3.08 | 0.06 | 0.02 | 4.87 | 4.64 | 0.09 | 0.10 | 5.04 | 4.80 | 0.12 | 0.11 | 5.10 | 4.86 | 0.12 | 0.12 |
| Fe | 3.45 | 3.33 | 0.14 | 0.04 | 3.82 | 3.71 | 0.05 | 0.06 | 3.92 | 3.76 | 0.07 | 0.08 | 3.93 | 3.80 | 0.07 | 0.06 |
| Co | 2.51 | 2.47 | 0.12 | 0.04 | 2.73 | 2.65 | 0.03 | 0.05 | 2.42 | 2.34 | 0.04 | 0.04 | 2.77 | 2.69 | 0.05 | 0.04 |
| Ni | 1.39 | 1.54 | 0.11 | 0.04 | 2.29 | 1.61 | 0.02 | 0.08 | 1.17 | 1.11 | 0.02 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 |
| Cu | 0.27 | 0.45 | 0.12 | 0.04 | 0.20 | 0.01 | 0.00 | 0.00 | 0.03 | 0.03 | 0.02 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 |
The C28 cage structure possesses zero MM, however, when encapsulated with TMs, it acquires finite MM. In TM@C28 complexes, MM is mainly localized at the TM site (see Fig. 8) with a small amount of MM induced on surrounding C atoms. The total MM ranges from 2 μB in Ti@C28 to 1 μB in Cu@C28. However, the total MM of Cr@C28 increases to 4 μB from 0 μB in C28 cage. In Cu@C28, 0.2 μB of a total MM of 1 μB is localized at the Cu atom. The magnetic interaction of Ti, V, Mn, Fe, Co and Cu with the surrounding C atoms is of FM nature except for Ni which shows antiferromagnetic (AFM) interactions.
The C32 and C36fullerene structures are non-magnetic in their ground state. However, when encapsulated with TMs, the resultant complex becomes magnetic. Similar to the trend observed in the smaller fullerenes, C32 and C36 also have MM localized mainly at the TM sites, as shown in Table 4, except for Co, Ni and Cu (see Fig. 8). Interestingly, Ni@C32 and Ni@C36 show zero MM. The LMM at the Ni site in Ni@C32 is 1.17 μB with a major contribution from 3d orbital electrons, whereas in Ni@C36 complex, LMM is zero. The surrounding C atoms interact AFM with Ti, V, Cr, Mn, Co and Ni. The Cu@C32 complex shows a MM of 1 μB but with nearly no contribution from TM and all the MM is contributed by the cage C atoms.
Inside C36, the TMs show a mixed behavior as Ti, V, and Mn show AFM interactions, whereas Cr, Fe, Co and Cu show FM interactions with the cage C atoms. In TM@C36 complexes, the majority contribution to MM is localized at the TM site with a maximum contribution from 3d orbitals, apart from Cr and Cu (see Table 4).
At this point, we would like to present the magnetic behavior of complexes when 3d TM is substituted on the surface of the fullerenes for assessment, although total energy calculations have suggested larger stability of the endohedral complexes. The total magnetic moment and local magnetic moment of Cn−1TM for n = 32 and 36 are presented in the Table 5.
| TM | C32 | C36 | ||
|---|---|---|---|---|
| μ T | μ TM | μ T | μ TM | |
| Sc | 1.0 | 0.00 | 1.0 | 0.01 |
| Ti | 0.0 | 0.00 | 0.0 | 0.01 |
| V | 1.0 | 2.90 | 1.0 | 2.93 |
| Cr | 2.0 | 4.03 | 2.0 | 4.01 |
| Mn | 3.0 | 4.64 | 3.0 | 4.87 |
| Fe | 4.0 | 4.18 | 2.0 | 4.08 |
| Co | 1.0 | 1.11 | 1.0 | 1.13 |
| Ni | 0.0 | 0.00 | 2.0 | 2.26 |
| Cu | 1.0 | 0.00 | 1.0 | 0.01 |
From Table 5, the 3d TMs towards the left of Mn in the periodic table shows distinct magnetic behavior when substituted on the surface with a different value of total MM as compared to endohedral metallofullerene complexes. Towards the right of Mn in the 3d series, the MM of the surface doped fullerene complexes shows a similar pattern to TM@Cn complexes.
The MMs of TM@Cn complexes are dependent on nature of TM and the size of encapsulating fullerenes. The atomic MMs of 3d TMs are altered to a large extent inside the fullerene cage. For Cr, the MM increases from 0.0 μB in C20 to 5.99 μB in C36. Interestingly for Mn, the MM is constant in all fullerenes from C20 to C36. For Fe, the MM decreases from 8 μB in C20 to 3.99 μB in C36. For Co, the MM decreases from 7.0 μB in C20 to 1.0 μB in C32 and then increases to 3.0 μB in C36. There is a small induced MM on the nearest C atoms in all fullerenes which aligns FM for n < 32 and AFM for n ≥ 32, with some exceptional cases.
IV. Conclusions
We have investigated a possibility of inducing magnetism in small carbon fullerenes by encapsulating magnetic 3d TM impurities using spin polarized DFT. The average diameters of the fullerene cages show a small increase on TM encapsulation. The cohesive energy describes reliably the element’s ability to be trapped inside fullerene but do not tell us much about the energetics of the formation process. The cohesive energy of TM@Cn complexes suggest that Ti and V are stable inside all cage structures, therefore indicating a strong possibility of their production. The C28 cage is the smallest fullerene which can encapsulate all 3d TMs except Cr and Cu which can only be encapsulated inside the C36 cage. Cu is found to be least stable for encapsulation. The stability of substitutional metallofullerenes is found to improve with higher atomic number TMs, which is contrary to the pattern observed in similar sized endohedral fullerenes. The MM is induced in all fullerene cages with the introduction of TM impurity at the endohedral site. There is a significant MM of the order 0.12–0.50 μB induced on the carbon cage atoms. All the 3d TMs in C20 and C28 cages interact with C atoms ferromagnetically except Ni@C28 which interacts antiferromagnetically. Ti, V, Cr, and Mn show AFM interactions with C atoms of C36 cage. Therefore, it may be concluded that there is a transition of magnetic interactions from FM to AFM for n = 32. The MM is quenched for Ni beyond C32. It does not show any change for Mn@Cn, although a FM to AFM change does take place at n = 32. Thus, the magnetic behavior of TM@Cn complexes is dependent on the size of the fullerene cages, configuration of 3d metals and the type of magnetic interactions between TMs and surrounding C atoms. The fullerene molecule acquires spin and charge and becomes magnetic due to the spin and charge transfer from transition metal dopants. Therefore, the choice of TM and host fullerenes provides a novel possibility to control the magnetic behavior of carbon systems. Further, given suitable experimental conditions, these small metallofullerenes should therefore be producible in abundance, facilitating the production of fullerene-based magnetic materials.Acknowledgements
Authors are thankful to SIESTA group for providing their computational code. Isha Garg is thankful to University Grant Commission for providing financial support.References
- Carbon Based Magnetism, ed. T. L. Makarova and F. Palacio, Elsevier, Amsterdam, 2006 Search PubMed.
- D. S. Bethune, R. D. Johnson, J. R. Salem, M. S. de Vries and C. S. Yannoni, Nature, 1993, 366, 123 CrossRef CAS.
- R. Valencia, A. Rodriguez-Fortea and J. M. Poblet, Chem. Commun., 2007, 4161 RSC.
- J. Lu, R. Sabirianov, W. N. Mei, Yi Gao, C.-G. Duan and X. Zeng, J. Phys. Chem. B, 2006, 110, 23637 CrossRef CAS.
- H. Shinohara, Rep. Prog. Phys., 2000, 63, 843 CrossRef CAS.
- F. Lopez-Urias, E. Cruz-Silva, E. Munoz-Sandoval, M. Torrones and H. Terrones, J. Mater. Chem., 2008, 18, 1535 RSC.
- R. H. Xie, G. W. Bryant, G. Sun, T. Kar, Z. Chen, V. H. Smith Jr, Y. Araki, N. Tagmatarchis, H. Shinohra and O. Ito, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 201403 CrossRef.
- R. B. Ross, C. M. Cardona, D. M. Guldi, S. G. Sankaranarayanan, M. O. Reese, N. Kopidakis, J. Peet, B. Walker, G. C. Bazan, E. V. Keuren, B. C. Holloway and M. Drees, Nat. Mater., 2009, 8, 208 CrossRef CAS.
- N. Weiden, B. Goedde, H. KaB and K.-P. Dinse, Phys. Rev. Lett., 2000, 85, 1544 CrossRef CAS.
- H. Kietzmann, R. Rochow, G. Gantefor, W. Eberhardt, K. Vietze, G. Seifert and P. W. Fowler, Phys. Rev. Lett., 1998, 81, 5378 CrossRef CAS.
- P. Mroz, A. Pawlak, M. Satti, H. Lee, T. Wharton, H. Gali, T. Sarna and M. R. Hamblin, Free Radical Biol. Med., 2007, 43, 711 CrossRef CAS.
- J. Liu, S. Ohta, A. Sonoda, M. Yamada, M. Yamamoto, N. Nitta, K. Murata and Y. Tabata, J. Controlled Release, 2007, 117, 104 CrossRef CAS.
- H. W. Kroto, Nature, 1987, 329, 529 CrossRef CAS.
- G. von Helden, N. G. Gotts and M. T. Bowers, Nature, 1993, 363, 60 CrossRef CAS.
- C. Piskoti, J. Yatger and A. Zettl, Nature, 1998, 393, 771 CrossRef CAS.
- H. Prinzbach, A. Weller, P. Landenberger, F. Wahl, J. Worth, L. T. Scott, M. Gelmont, D. Olevano and B.v. Issendorff, Nature, 2000, 407, 60 CrossRef CAS.
- P. R. C. Kent, M. D. Towler, R. J. Needs and D. Rajagopal, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15394 CrossRef CAS.
- T. Gau, M. D. Diener, Yan Chai, M. J. Alford, R. E. Haufler, S. M. McClure, T. Ohno, J. H. Weaver, G. E. Scuseria and R. E. Smalley, Science, 1992, 257, 1661 CrossRef CAS.
- T. Gau, R. E. Smalley and G. E. Scuseria, J. Chem. Phys., 1993, 99(1), 352 CrossRef CAS.
- L. Sun, Y. Chang, B. Hong and R. Wang, Int. J. Quantum Chem., 2007, 107, 1241 CrossRef CAS.
- Yi-Ming Chen, Jing Shi, Lei Rui and Q.-X. Guo, THEOCHEM, 2009, 907, 104 CrossRef CAS.
- H. S. Kang, J. Phys. Chem. A, 2006, 110, 4780 CrossRef CAS.
- P. Ordejon, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter, 1996, 53, R10441 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425 CrossRef CAS.
- O. F. Sankey and D. J. Niklewski, Phys. Rev. B: Condens. Matter, 1989, 40, 3979 CrossRef.
- H. Sharma, I. Garg, K. Dharamvir and V. K. Jindal, J. Phys. Chem. A, 2009, 113, 9002 CrossRef CAS.
- H. Sharma, I. Garg, K. Dharamvir and V. K. Jindal, J. Comput. and Theoret. Nanoscience, 2010 Search PubMed , in press.
- H. Sharma, I. Garg, K. Dharamvir and V. K. Jindal, J. Phys. Chem. C, 2010, 114, 9153 CrossRef CAS.
- G. Rollmann, P. Entel and S. Sahoo, Comput. Mater. Sci., 2006, 35, 275 CrossRef CAS.
- M. Kabir, A. Mookerjee and D. G. Kanhere, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224439 CrossRef.
- J. M. Lopez, A. H. Romero, M. E. Gracia and J. L. Moran-Lopez, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 140405 CrossRef.
- C. J. Barden, J. C. Rienstra-Kiracofe and H. F. Schaefer, J. Chem. Phys., 2000, 113, 690 CrossRef CAS.
- E. Malolepsza, H. A. Witek and S. Irle, J. Phys. Chem. A, 2007, 111, 6649 CrossRef CAS.
- M. J. Han, G. Kim, J. II Lee and J. Yu, J. Chem. Phys., 2009, 130, 184107 CrossRef.
- H. Kietzmann, R. Rochow, G. Gantefr, W. Eberhardt, K. Vietze, G. Seifert and P. W. Fowler, Phys. Rev. Lett., 1998, 81, 5378 CrossRef CAS.
- G. Galli, F. Gygi and J. Christophe Golaz, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1860 CrossRef CAS.
- L. S. Wang, J. M. Alford, Y. Chai, M. Diener, G. E. Scuseria and R. E. Smalley, Chem. Phys. Lett., 1993, 207, 354 CrossRef CAS.
- X. Lu and Z. Chen, Chem. Rev., 2005, 105, 3643 CrossRef CAS.
- M. Sparta, V. R. Jensen and K. J. Borve, Fullerenes, Nanotubes, Carbon Nanostruct., 2006, 14, 269 Search PubMed.
| This journal is © The Royal Society of Chemistry 2011 |
