The binding of polyvalent galactosides to the lectin Ricinus communis agglutinin 120 (RCA120): an ITC and SPR study†
Sebastian G.
Spain
*a and
Neil R.
Cameron
*b
aSchool of Pharmacy, Boots Science Building, University of Nottingham, Nottingham, NG7 2RD, UK. E-mail: sebastian.spain@nottingham.ac.uk; Tel: +0115 8466241
bDepartment of Chemistry, University of Durham, University Science Laboratories, South Road, Durham, DH1 3LE, UK. E-mail: n.r.cameron@durham.ac.uk; Tel: +0191 3342008
First published on 4th April 2011
Abstract
Mono- and polyvalent galactosides have been investigated with respect to their binding to the plant lectin Ricinus communis agglutinin 120 (RCA120). Thermodynamic parameters (Ka, ΔG, ΔH, ΔS and n) have been determined by isothermal titration calorimetry (ITC) and kinetics of binding (ka and kd) measured by surface plasmon resonance (SPR). ITC analysis using a single set of sites model found a non-statistical increase in avidity with increasing valency with the largest ligand displaying a greater than 20-fold increase in Ka compared to its monomeric precursor after correction for valency; binding was found to be enthalpically driven. SPR analysis supports the avidity increase but values of Ka observed were up to 100-fold greater than those measured by ITC. The large discrepancy between the two measurements is rationalized by the polyvalent–polyvalent interaction that is measured by SPR.
1 Introduction
Many biological recognition events are mediated via binding interactions between carbohydrates and carbohydrate-binding proteins known as lectins. The interaction between carbohydrates and lectins is unusually weak compared to others in Nature with association constants typically in the millimolar range (cf. 105–1010 M−1 for enzyme–substrate or antibody–antigen interactions). Despite this weakness of binding carbohydrate–lectin interactions display high specificity; it is uncommon to find a lectin that binds both galactose and glucose, although some variation in structure is allowed.1 The ubiquity and specificity of lectins makes them an attractive targeting mechanism for drug-delivery, an area that has recently been reviewed,2 but for this to be successful an increase in avidity is required. Here, as is often the case, Nature has already provided a solution – multivalency – lectins and their corresponding ligands are usually presented in clustered arrays of high valency. The increased avidity through multivalency is unusual as the relationship is non-linear and thus not an artifact of increased local concentration. This was well illustrated by Lee et al. who found that lectin-binding of lactosamine derivatives increased over 100-fold when the number of carbohydrate moieties was increased from 1 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and have dubbed this the clusterglycoside effect.4,5 In the decades since Lee et al.'s discovery there has been much research into the cluster glycoside effect and its origins.5 Several mechanisms for the enhanced avidity have been postulated including the chelate effect, where a ligand binds to multiple sites on the same lectin simultaneously,6 and “bind and slide”, where lectins can diffuse internally between carbohydrates on the same ligand.7
3 and have dubbed this the clusterglycoside effect.4,5 In the decades since Lee et al.'s discovery there has been much research into the cluster glycoside effect and its origins.5 Several mechanisms for the enhanced avidity have been postulated including the chelate effect, where a ligand binds to multiple sites on the same lectin simultaneously,6 and “bind and slide”, where lectins can diffuse internally between carbohydrates on the same ligand.7
To further investigate the cluster glycoside effect, access to multivalent ligands is required. Multivalent glycoconjugates based upon dendrimers, lipids (e.g. micelles and liposomes) and nanoparticles have been investigated with regard to their lectin binding but are often, in the case of dendrimers, difficult to synthesise or, for lipids and nanoparticles, their structures are ill-defined making elucidation of structure–activity relationships, and subsequent mechanistic derivation, complex. Glycopolymers are a family of glyconjugates based upon synthetic polymer backbones that are of interest as drug-delivery vehicles and macromolecular therapeutics due to their ability to access the cluster glycoside effect using relatively facile chemistry.8 Recent developments in polymer chemistry have allowed the synthesis of complex, polyvalent glycopolymers of defined valency and architecture;9,10 consequently they have been studied extensively with respect to lectin binding.11
Herein we describe the synthesis of a series of mono- and polyvalent galactoside ligands via reversible addition–fragmentation chain transfer (RAFT) polymerisation; their interactions with the plant lectin Ricinus communis agglutinin 120 by isothermal titration calorimetry and surface plasmon resonance and the implications of these with respect to the origins of the cluster glycoside effect.
2 Results and discussion
2.1 Synthesis of galactoside ligands
2-(β-D-galactosyloxy)ethyl methacrylate (1) was synthesised in two steps from β-D-galactose pentaacetate and 2-hydroxyethyl methacrylate (HEMA) viaboron trifluoride promoted glycosylation (Fig. 1).12,13 Glycosyl 2-O-acetates are considered to be “disarmed”, that is they are relatively poor glycosyl donors, and consequently require long reaction times to achieve high levels of glycosylation. Deng et al. recently reported the acceleration of Lewis acid promoted glycosylation by the use of sonication14 and, when used in conjunction with an excess of the glycosyl donor, complete glycosylation of HEMA was achieved in 45 min with no loss of anomeric selectivity. After deprotection and purification by standard methods the desired product was isolated in good yield (typically ∼50% overall). | ||
| Fig. 1 Synthesis of the mono- and polyvalent ligands studied. Reaction conditions: i. 2-hydroxyethyl methacrylate, BF3·Et2O, DCM, sonication; ii. damp MeOH, K2CO3; iii. (4-cyanopentanoic acid)-4-dithiobenzoate, 4,4′-azo(4-cyanopentanoic acid), water/EtOH, 70 °C. | ||
Polyvalent ligands were synthesised by RAFT polymerisation of 1 in aqueous ethanol using (4-cyanopentanoic acid)-4-dithiobenzoate and 4-4′-azobis(4-cyanopentanoic acid) as the chain transfer agent (CTA) and initiator respectively; different valencies were targeted by varying the [monomer]/[CTA] ratio. Residual 1 and other low molecular weight impurities were removed by thorough dialysis against high purity water (MWCO 3.5 kDa). Molecular weights, polydispersity indices and hydrodynamic radii were determined using aqueous size exclusion chromatography and dynamic light-scattering; the average valency of each ligand was determined from the value of Mn (Table 1).
| Ligand | M n a (kDa) | M w/Mna | Valency | D h b (nm) | D h c (nm) | l d (nm) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Measured using triple detection aqueous size exclusion chromatography. b Determined by dynamic light-scattering in HEPES buffer. c Determined by dynamic light-scattering in PBS. d Approximate fully extended chain length assuming a C–C bond length of 1.54 Å and a dihedral angle of 109.5°. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | n/a | n/a | 1 | n/a | n/a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 20.1 | 1.15 | 68 | 5.4 | 6.6 | 17.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 42.3 | 1.11 | 144 | 8.0 | 7.2 | 36.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 56.6 | 1.10 | 193 | 23.4 | 30.8 | 46.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 11.0 | 1.10 | 37 | 4.6 | 5.2 | 9.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2 Binding interactions between RCA120 and galactoside ligands
The binding between the lectin Ricinus communis agglutinin 120 (RCA120) and a series of β-D-galactose bearing ligands was subjected to two forms of analysis: isothermal titration calorimetry (ITC) and surface plasmon resonance (SPR). Although these techniques provide similar information regarding binding events they are complementary, allowing investigation of different aspects of the binding event. ITC allows the determination of the thermodynamics of a binding event and can thus provide an insight into its mechanism, for example entropically driven events are likely to involve the displacement of water or other small ligands from the protein binding site.15SPR is more comparable to how the binding event may occur in vivo, where it is likely that lectins will be clustered on a cell surface with the ligand flowing past transiently. RCA120 was chosen because initial SPR studies using peanut agglutinin (PNA) found the binding to be so weak as to be undetectable by this method. This is unlikely to be due to genuinely weak interaction with the polymers as their binding to PNA has previously been demonstrated by ITC.16 Instead, it is likely to be due to the lectin binding preferentially to the carboxylated methylcellulose coating on the SPR chip to which it is attached covalently preventing the ligand access to its recognition domain. Similar effects have been reported before by Kamerling et al.172.3 Isothermal titration calorimetry
Isothermal titration calorimetry has previously been used to investigate the binding of poly[2-(β-D-galactosyloxy)ethyl methacrylate] to PNA. The polymers investigated were synthesised by standard free radical polymerisation, consequently molecular weight was uncontrolled and those investigated were disparate: one low (Mn ∼ 3 kDa, Mw/Mn = 2.15), the other high (Mn ∼ 461 kDa, Mw/Mn = 2.21).16 Here a set of polymers of intermediate molecular weights (20 ≤ Mn ≤ 60 kDa), in addition to the monomeric species, were compared with respect to their binding to RCA120. Experiments were conducted by a standard protocol and heats of dilution/mixing were determined by titration of the carbohydrate ligands into buffer alone and subtracted from the values for ligand–lectin binding. In all cases the Wiseman parameter, c, was in the range 1–100.18Calorimetry data was analysed using Origin 7.0 Pro (OriginLab). Due to its potential toxicity, RCA120 was not commercially available as a lyophilised powder, only as a buffered solution. Consequently RCA120 was buffer exchanged prior to use to ensure the same buffers were used for both ligand and receptor. The concentration of the resulting solution was determined by UV spectroscopy using a value of A1% of 15.7 at 280 nm.19 Some RCA120 precipitation was observed upon storage, consequently concentrations were redetermined prior to each experiment.The previous study on poly[2-(β-D-galactosyloxy)ethyl methacrylate] binding to PNA noted that the “single set of sites” model (SSoS) within the ITC software did not produce adequate fitting to derive thermodynamic parameters; a problem attributed to precipitation of polymer–protein aggregates formed upon binding.16 Instead they used a more complex model that introduced a second enthalpic term to allow for the heat change due to the precipitation. However, it should be noted that greatest enthalpic contribution for precipitation observed was for the monomeric ligand 1 which should be incapable of causing lectin precipitation through multiple binding and questions the validity of this model. Additionally RCA120 is approximately half the size of PNA and only has 2 carbohydrate binding sites (cf. 4 on PNA) making lectin cross-linking less likely and Brewer et al. have reported successful derivation of thermodynamic parameters with multivalent ligands using the SSoS model when the concentrations of ligand and lectin were such that no precipitation was observed.20, 21 Here, although a small quantity of precipitation was observed when the largest ligand was used, the SSoS model was found to fit adequately. Fig. 2 contains example raw calorimetry data, binding isotherm and curve of best fit for the binding between ligand 3 and RCA120. Despite the relatively poor quality of the raw data (Fig. 2A), baseline correction and processing within the software resulted in an isotherm with the expected sigmoidal shape and fitting resulted in a curve in close agreement to the data. As the RCA120 tetramer is known to have two identical binding sites19n was fixed at 2 for monomeric species to simplify fitting. The ITC data were also analysed using a modified Scatchard analysis previously described by Brewer et al.20,21 This methodology introduces an additional term for the functional valency of the ligand allowing the construction of Scatchard plots for multivalent ligands (see Materials and methods for details).
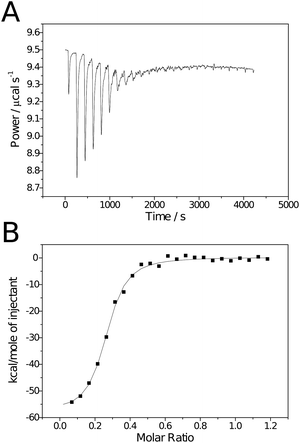 | ||
| Fig. 2 Raw (A) and processed (B) isotherms for the binding of polymeric ligand 3 to RCA120. | ||
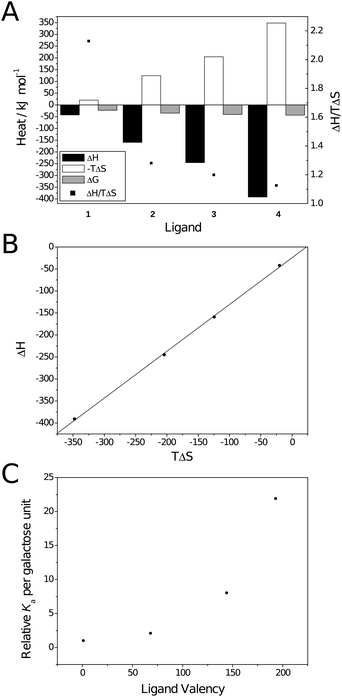 | ||
| Fig. 3 Thermodynamic plots for the binding between galactoside ligands and RCA120. (A) Thermodynamic parameters; (B) Compensation plot (—) Linear fit. R2 = 0.999, slope = 1.06; (C) Valency corrected Kaversus ligand valency. | ||
| Ligand | ΔHobsa (kJ mol−1) | ΔGobsa (kJ mol−1) | TΔSobsa (kJ mol−1) | K a/M−1 | β c | n d | 1/n | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSoSb | Scatchard | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a As molarities rather than activities were used the values are reported as observed. b “Single set of sites” model. c Defined as the ratio of polyvalent and monovalent interaction.22 d Stoichiometry with respect to lectin, i.e. number of ligands per RCA120 tetramer. e n was fixed during curve fitting to allow calculation of K and ΔH. f Calculated from isotherm without subtraction of heats of dilution. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | −42.4 | −22.5 | −19.9 | 8.74 × 103 | 7.19 × 103 | 1 | 2e | 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | −159 | −34.8 | −124 | 1.24 × 106 | 1.06 × 106 | 140 | 0.224 | 4.46 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | −245 | −40.7 | −204 | 1.01 × 107 | 9.87 × 106 | 1155 | 0.255 | 3.92 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | −391 | −43.7 | −347 | 3.69 × 107 | 3.58 × 107 | 4222 | 0.130 | 7.69 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3f | −242 | −40.1 | −202 | 1.07 × 107 | n/a | 1224 | 0.260 | 3.85 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For the polyvalent ligands, enthalpically driven binding is contrary to both modelled behaviour for multivalent binding23 and that reported by Ambrosi et al.16 The enthalpic driving force is confirmed by the compensation plot (Fig. 3B) which is linear with a slope greater than unity (1.06 ± 0.02; R2 = 0.999). The difference in thermodynamic behaviour between the two lectin bindings is probably due to a combination of effects. Ambrosi et al. partly attributed the entropic factor to displacement of water from the protein surface through aggregation. As aggregation was only observed to a slight degree here less of an entropic factor is likely. Similar behaviour has been reported by Brewer et al. for lectin binding of dendritic multivalent carbohydrates when aggregation was absent.20,21,24 Ambrosi et al. also noted that thermodynamic parameters were heavily influenced by ionic strength of the buffer used in the titration. Higher concentrations of salts resulted in an increased enthalpic contribution and a reduced entropic contribution; Ka was also reduced dramatically. This was particularly prominent when tris buffer was used, instead of citrate, with the binding becoming entropically disfavoured. It should also be noted that, due to the high heat of ionisation of tris (ΔHion ∼ 46 kJ mol−1),25 values may not have been completely accurate. Here, phosphate-buffered saline was used for all experiments due to the high solubility of RCA120 in this solution and its heats of ionisation being relatively low (– 1 ≤ ΔHion ≤ 4 kJ mol−1 depending on ionic strength).25 The minimal effect of buffer ionisation is confirmed by comparison of the thermodynamic parameters calculated with and without correction for heats of dilution/mixing for ligand 3 (entries 3 and 5 in Table 2) confirming that the lack of entropic contribution is not due to buffer choice.
Entropic favourability would also be likely if lectin binding leads to dispersion of polymer aggregates. Glycopolymers have already been shown to self-associate in aqueous solution26 with association attributed to intermolecular hydrogen bonding and hydrophobic interactions by the polymer backbone. Dynamic light-scattering at the same concentration used for ITC (see Table 1 for hydrodynamic diameters and ESI† for distributions) showed no evidence of aggregation for ligands 2 and 3. Ligand 4 is larger than expected when compared to the other ligands having a hydrodynamic radius 4-fold greater than ligand 3 despite only a <50% increase in molecular weight. It is unclear if this is due to aggregation as there is no evidence of a smaller species consistent with the unimolecular, unaggregated polymer and analysis at a 10-fold lower concentration showed no change in hydrodynamic radius. Consequently the large difference in hydrodynamic radius for ligands 3 and 4 may instead be due to a change in solution conformation with increasing molecular weight. Although dispersion of possible aggregates during binding is still a possibility the apparent solution stability of 4 suggests that these effects may be negligible. Overall binding would be expected to be entropically disfavoured as a bound polymer will have fewer possible solution conformations and thus a reduced number of degrees of freedom. This is particularly true where ligands are binding to multiple lectin moieties which both restricts the degrees of freedom and reduces the number of discrete species in solution.
Interestingly, as molecular weight increases, the ratio ΔH/TΔS decreases and tends towards 1 (black squares in Fig. 3A). Similar behaviour has been noted in dendritic systems where ΔH was seen to scale approximately with valency, i.e. for a tetravalent system ΔH was approximately 4-fold that of the monovalent, but −TΔS became more positive disproportionately.27 This behaviour was attributed to the inability of a relatively rigid ligand to fill both binding sites on an individual lectin, instead binding one lectin for each ligand presented, resulting in a greater entropic cost. The same explanation is possible here as, although the ligands in question are relatively flexible molecules, the two binding sites on RCA120 are approximately 11 nm apart (measured with Jmol28,29 using the Protein Data Bank file 1RZO30). The hydrodynamic diameter and fully extended chain lengths of ligands 2–4 are given in Table 1. From these it may be possible for 3 and 4 to bridge both sites but to do so would come at great entropic cost due to the restriction of the degrees of freedom on the polymer's conformation; particularly ligand 3 which would be very extended. Consequently it may be more entropically favourable to bind a single site of multiple RCA120 molecules which is supported by the values of 1/n (the number of lectins per ligand). Unsurprisingly the stoichiometry of the interaction also varies considerably with valency. More interestingly there is a decrease in stoichiometry between ligands 2 and 3. This may be an artifact of imperfect fitting of the SSoS model and will be discussed in more detail (vide infra).
Ligand 4 (average valency 193) has an overall avidity over 4000-fold greater than monomeric ligand 1; on a per sugar basis this 22-fold increase is no less striking. The non-linear behaviour observed is similar to that demonstrated by Kiessling et al. who also found a limiting molecular weight after which avidity no longer increased; this may also be the case here but would require larger ligands to be synthesised and analysed.6,31 Kiessling et al. attributed the large increase to the larger ligands' ability to bridge binding sites on a single lectin.
2.4 SPR analysis of multivalent–multivalent interactions between polyvalent galactoside ligands and RCA120
Several reports of studies of the interaction of glycopolymers with lectins viaSPR have been published.31–35 Only one has studied the interaction between an immobilised lectin and a glycopolymer in solution,35 the configuration closest to that likely in vitro and in vivo, and the one that allows investigation of the multivalent–multivalent interaction that occurs at a cell surface prior to e.g.endocytosis. For the experiments RCA120 was attached to the surface of a sensor chip at various levels of functionalisation (ca. 200, 2000 and 5000 response units) using a standard amine coupling protocol. Solutions of ligands 3 and 5, ranging in concentration from 500 pM to 10 μM, were prepared and analysed for the binding to each channel. Initial test runs found the binding to be too tight, with very long off times. To reduce this time, allowing rapid acquisition of another sample, an injection of methylβ-D-galactoside solution was performed. The blank was substracted from the functionalised channels to allow for non-specific binding. The channels with the lowest and highest levels of RCA120 modification were found to give too weak or too strong binding respectively. Sensorgrams were thus acquired on channel 2 (ca. 2000 RU RCA120) by a 180 s injection of the ligand and a 240 s off period. Between acquisitions a 30 s injection of methylβ-D-galactoside and 60 s off period were performed to return the surface to its background level.Sensorgrams for the two ligands at various concentrations are shown in Fig. 4. The data from these were fitted within the BIAcore software using a single sites (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Langmuir Binding) model. For each polymer five consecutive concentrations were chosen from those analysed; 5 nM–1 μM for ligand 5 and 500 pM–50 nM for ligand 3. The highest concentrations were removed as the binding was too rapid to enable accurate fitting. For ligand 5, the lowest two concentrations were removed as the response was too weak to allow accurate fitting. Thermodynamic and kinetic parameters for these polymers are shown in Table 3. As was seen with the ITC experiment, there is a large increase in Ka with increased molecular weight, here a ∼4-fold increase in valency leads to a near 8-fold increase in avidity. The larger polymer also displays more than a 100-fold increase in Ka compared to the value measured by ITC (1.39 × 109 M−1cf. 1.01 × 107 M−1); an increase attributable to the now multivalent–multivalent interaction. The kinetic parameters for the two ligands are more interesting. Despite the large difference in Ka there is less than a 2-fold difference in the association rate constant, ka. Looking at this value alone it would be expected that these ligands would have similar avidities. However, ligand 5 has a value of kd 5-fold higher than that of ligand 3 and, consequently, has a far lower avidity (Ka = ka/kd).
1 Langmuir Binding) model. For each polymer five consecutive concentrations were chosen from those analysed; 5 nM–1 μM for ligand 5 and 500 pM–50 nM for ligand 3. The highest concentrations were removed as the binding was too rapid to enable accurate fitting. For ligand 5, the lowest two concentrations were removed as the response was too weak to allow accurate fitting. Thermodynamic and kinetic parameters for these polymers are shown in Table 3. As was seen with the ITC experiment, there is a large increase in Ka with increased molecular weight, here a ∼4-fold increase in valency leads to a near 8-fold increase in avidity. The larger polymer also displays more than a 100-fold increase in Ka compared to the value measured by ITC (1.39 × 109 M−1cf. 1.01 × 107 M−1); an increase attributable to the now multivalent–multivalent interaction. The kinetic parameters for the two ligands are more interesting. Despite the large difference in Ka there is less than a 2-fold difference in the association rate constant, ka. Looking at this value alone it would be expected that these ligands would have similar avidities. However, ligand 5 has a value of kd 5-fold higher than that of ligand 3 and, consequently, has a far lower avidity (Ka = ka/kd).
2.5 Origins of the cluster glycoside effect in polyvalent galactosides
The thermodynamic and kinetic data above provide evidence that the avidity enhancement between polyvalent galactosides and RCA120 compared to their monomeric analogues has contributions from both the chelation mechanism used by Kiessling et al.6,31 and the “bind and slide/hop” mechanism observed with multivalent carbohydrates and mucins by Brewer et al.7,20,21,36 As observed by Kiessling et al. there is an exponential increase in avidity with valency. The small solution size of ligands 2 and 3 make it unlikely that they can bind both sites of RCA120 at least without considerable entropic cost, suggesting that the avidity increase is due to a “bind and slide” mechanism similar to that described by Brewer et al. A suggested mechanism of binding is proposed in Fig. 5. For the early injections, where the concentration of RCA120 is far greater than that of the ligand, ligands are rapidly bound by the excess lectin and a core–shell structure is formed with the ligand at the centre; as the shell is composed of lectin alone cross-linking is unable to occur. As the ligand concentration is increased a second shell of ligand is formed around the first creating a glycosylated shell that, again, prevents cross-linking and macroscopic precipitation. The far smaller size of the ligand compared to the ligand–lectin aggregates and, consequently, their higher diffusion rate makes formation of the multi-layer structure kinetically favourable compared to the formation of crosslinks. The reduced mobility of RCA120 and the ligands results in a dynamic equilibrium where an unbinding event is rapidly counteracted by rebinding of a galactose moiety on the same or a neighbouring ligand. This mechanism is supported by the enthalpic nature of the interaction and disfavourable entropic factor. Investigation of the solution structure throughout the binding experiment may allow elucidation of this mechanism. For ligand 4, which appears to have a larger, possibly extended, structure in solution, it is likely that the same mechanism is occurring but, due to its lower mobility, it is kinetically less favoured for multi-layer structures to form before macroscopic precipitation can occur.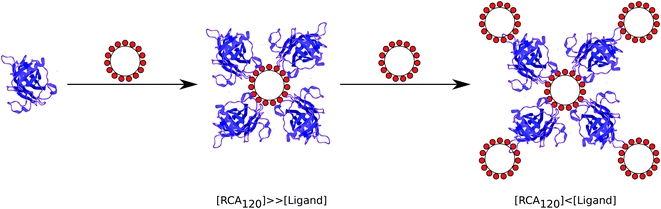 | ||
| Fig. 5 Schematic of the possible binding mechanism between RCA120 and polyvalent galacotsides. | ||
The SPR data also supports a “bind and slide” type mechanism. Ligand 5 is too small to be able to bind both sites on RCA120 as its fully extended chain length is ≤10 nm. It is also unlikely that it could bind two neighbouring lectins on the surface as the modification density was relatively low. Consequently its high avidity for the lectin-coated surface can only arise from rapid association following a dissociation event resulting in a low overall dissocation rate. 3 may be able to bind two sites simultaneously but to do so would require a conformational change compared to its solution structure and the SPR “two state–conformational change” model was found to fit poorly to the data. Additionally, the increased avidity of 3cf.5 is dominated by a decreased off rate which is in agreement with a “bind and slide” type mechanism and an increased probability of rebinding. If the ligands are approximated to a deformable sphere then they can be considered to have a footprint that will be proportional to their radius. In the same manner, a tyre of a larger diameter will maintain a larger contact area with the road than a smaller one; assuming all other factors to be the same. Deformable spheres have been modelled to roll along ‘sticky’, i.e. interacting, surfaces,37,38 a phenomenon that has also been modelled and observed experimentally in leukocytes.39,40 An increased contact area during rolling will result in a greater probability of secondary binding events occuring, resulting in increased retention on the surface. Thus smaller polymers, with their reduced footprints will be shed more readily, increasing kd values.
3 Materials and methods
3.1 Materials
(4-Cyanopentanoic acid)-4-dithiobenzoate was synthesised according to literature41 and isolated as a pink crystalline solid. β-D-Galactose pentaacetate (98%), 2-hydroxyethyl methacrylate (98%, HEMA) and potassium carbonate (99%) were purchased from Aldrich. Boron trifluoride diethyl etherate (purum, dist.) and 4,4′-azobis(4-cyanopentanoic acid) (98%) were purchased from Fluka. Amberjet 1200H strong acid cation exchange resin was purchased from Fisher. RCA120 was purchased from Vector Labs and was supplied as 5 mg mL−1 solution in PBS. All solvents were Fisher HPLC grade, when anhydrous solvents were required they were dried using an Innovative Technologies Pure Solv system using alumina columns and stored under nitrogen prior to use. Ultra-high quality (UHQ) water (≥18 MΩ resistivity) was obtained using a Purite Neptune water purification system. All other chemicals were used without further purification. Gradient flash column chromatography was performed using a Biotage SP1 automated purification system using pre-packed silica columns.3.2 Ligand synthesis
2-(β-D-galactosyloxy)ethyl methacrylate and its polymers were synthesised as previously described.12,13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, hexane–ethyl acetate).
3, hexane–ethyl acetate).
Found C, 51.88; H, 6.18; C20H28O12 requires C, 52.17; H, 6.13. FT-IRν/cm−1: 1751 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of acetate groups) 1719 (C
O of acetate groups) 1719 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of methacrylate ester) 1637, 1320, 1298 (C
O of methacrylate ester) 1637, 1320, 1298 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). δH: (400 MHz, CDCl3) 1.98 (3H, s, 3 × H-3), 2.01, 2.04, 2.05, 2.15, (3H × 4, 4s, Ac × 4), 3.84 (1H, ddd, J6a, 6b 11.5 Hz, J5a, 6a 7.5 Hz, J5b, 6a 4.0 Hz, H-6a), 3.92 (1H, td, Jt = J5′, 6a′ = J5′, 6b′ 6.6 Hz, Jd = J4′, 5′ 1.1 Hz, H-5′), 4.06 (1H, ddd, J6a, 6b 11.6 Hz, J5b, 6b 5.9 Hz, J5a, 6b 3.7 Hz, H-6b), 4.10 (1H, dd, J6′a, 6′b 10.3 Hz, J5′, 6′a 6.7 Hz, H-6′a), 4.18 (1H, dd, J6′a, 6′b 10.9 Hz, J5′, 6′b 6.5 Hz, H-6′b), 4.29 (2H, m, H-5a,b), 4.55 (1H, d, J1′, 2′ 8.05 Hz, H-1′), 5.01 (1H, dd, J2′, 3′ 10.4 Hz, J3′, 4′ 3.6 Hz, H-3′), 5.23 (1H, dd, J2′, 3′ 10.4 Hz, J1′, 2′ 8.0 Hz, H-2′), 5.39 (1H, dd, J3′, 4′ 4.5 Hz, J4′, 5′ 1.2 Hz H-4′), 5.59–5.61 (1H, m, H-1 Z to Me–C
C). δH: (400 MHz, CDCl3) 1.98 (3H, s, 3 × H-3), 2.01, 2.04, 2.05, 2.15, (3H × 4, 4s, Ac × 4), 3.84 (1H, ddd, J6a, 6b 11.5 Hz, J5a, 6a 7.5 Hz, J5b, 6a 4.0 Hz, H-6a), 3.92 (1H, td, Jt = J5′, 6a′ = J5′, 6b′ 6.6 Hz, Jd = J4′, 5′ 1.1 Hz, H-5′), 4.06 (1H, ddd, J6a, 6b 11.6 Hz, J5b, 6b 5.9 Hz, J5a, 6b 3.7 Hz, H-6b), 4.10 (1H, dd, J6′a, 6′b 10.3 Hz, J5′, 6′a 6.7 Hz, H-6′a), 4.18 (1H, dd, J6′a, 6′b 10.9 Hz, J5′, 6′b 6.5 Hz, H-6′b), 4.29 (2H, m, H-5a,b), 4.55 (1H, d, J1′, 2′ 8.05 Hz, H-1′), 5.01 (1H, dd, J2′, 3′ 10.4 Hz, J3′, 4′ 3.6 Hz, H-3′), 5.23 (1H, dd, J2′, 3′ 10.4 Hz, J1′, 2′ 8.0 Hz, H-2′), 5.39 (1H, dd, J3′, 4′ 4.5 Hz, J4′, 5′ 1.2 Hz H-4′), 5.59–5.61 (1H, m, H-1 Z to Me–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 6.13–6.14 (1H, m, H-1 E to Me–C
C), 6.13–6.14 (1H, m, H-1 E to Me–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). δC: (100.26 MHz, decoupled, 1H 400 MHz; CDCl3) 18.25 (C-3), 20.6, 20.8, 21.0 (4 × H3CCO2, 2 resonances overlap), 61.3 (C-6′), 63.5 (C-5), 66.8 (C-4′), 67.4 (C-6), 68.7 (C-2′), 70.7 (C-3′), 70.9 (C-5′), 101.3 (C-1′), 125.9 (C-1), 136.1 (C-2), 167.1 (C-4), 169.4, 170.2, 170.3 (MeCO2). LR-MS (ES+) m/z requires 483.4, found 483.2 (M + Na+).
C). δC: (100.26 MHz, decoupled, 1H 400 MHz; CDCl3) 18.25 (C-3), 20.6, 20.8, 21.0 (4 × H3CCO2, 2 resonances overlap), 61.3 (C-6′), 63.5 (C-5), 66.8 (C-4′), 67.4 (C-6), 68.7 (C-2′), 70.7 (C-3′), 70.9 (C-5′), 101.3 (C-1′), 125.9 (C-1), 136.1 (C-2), 167.1 (C-4), 169.4, 170.2, 170.3 (MeCO2). LR-MS (ES+) m/z requires 483.4, found 483.2 (M + Na+).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, MeCN–H2O). When the product of methacrylate ester cleavage was seen in the TLC (Rf 0.15) the reaction was neutralized by filtering into a flask containing Amberjet 1200H (H+) cation exchange resin and the mixture was stirred for 15 min. [NB: The deprotection reaction can proceed very rapidly; to prevent loss of the product due to methacrylate cleavage, ensure that the apparatus for filtration and neutralization are set up and ready for use before addition of K2CO3]. The resin was removed by filtration and the solvent was removed under reduced pressure. The resulting oil was purified by column chromatography (CHCl3–MeOH, gradient elution) to yield a colorless oil which became a white amorphous solid upon lyophilising. The product was dissolved in D2O to give a 0.50 M solution that was stored at −18 °C.
1, MeCN–H2O). When the product of methacrylate ester cleavage was seen in the TLC (Rf 0.15) the reaction was neutralized by filtering into a flask containing Amberjet 1200H (H+) cation exchange resin and the mixture was stirred for 15 min. [NB: The deprotection reaction can proceed very rapidly; to prevent loss of the product due to methacrylate cleavage, ensure that the apparatus for filtration and neutralization are set up and ready for use before addition of K2CO3]. The resin was removed by filtration and the solvent was removed under reduced pressure. The resulting oil was purified by column chromatography (CHCl3–MeOH, gradient elution) to yield a colorless oil which became a white amorphous solid upon lyophilising. The product was dissolved in D2O to give a 0.50 M solution that was stored at −18 °C.
Found C, 49.12; H, 6.94; C12H20O8 requires C, 49.31; H, 6.90. FT-IR (NaCl Plates) ν/cm−1: 3360 (br, OH), 1708 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of methacrylate ester) 1636, 1320, 1298 (C
O of methacrylate ester) 1636, 1320, 1298 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). δH: (500 MHz; D2O) 1.94 (3H, m, 3 × H-3), 3.48 (1H, dd, J2′, 3′ 9.7 Hz, J3′, 4′ 3.3 Hz, H-3′), 3.53 (2H, dt, Jt 5.09 Hz, Jd 5.7 Hz, H-5′), 3.74 (2H, m, H-6′) 3.84 (1H, m, H-4′) 3.86 (1H, ddd, J6a, 6b 11.8, J5b, 6b 6.0, J5b, 6a 3.8 Hz, H-6a) 4.12 (1H, ddd,J6a, 6b 11.6, J5b, 6b 5.9, J5a, 6b 3.7 Hz, H-6b) 4.29 (1H, d, 7.5, H-1′) 4.35 (2H, m, H-5) 5.64 (1H, m, H-1 Z to Me–C
C). δH: (500 MHz; D2O) 1.94 (3H, m, 3 × H-3), 3.48 (1H, dd, J2′, 3′ 9.7 Hz, J3′, 4′ 3.3 Hz, H-3′), 3.53 (2H, dt, Jt 5.09 Hz, Jd 5.7 Hz, H-5′), 3.74 (2H, m, H-6′) 3.84 (1H, m, H-4′) 3.86 (1H, ddd, J6a, 6b 11.8, J5b, 6b 6.0, J5b, 6a 3.8 Hz, H-6a) 4.12 (1H, ddd,J6a, 6b 11.6, J5b, 6b 5.9, J5a, 6b 3.7 Hz, H-6b) 4.29 (1H, d, 7.5, H-1′) 4.35 (2H, m, H-5) 5.64 (1H, m, H-1 Z to Me–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 6.14 (1H, m, H-1 E to Me–C
C) 6.14 (1H, m, H-1 E to Me–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); δC: (100.62 MHz; decoupled 1H 500 MHz; D2O) 18.4 (C-3), 62.5 (C-6′), 65.3 (C-5), 68.5 (C-6), 70.3 (C-4′), 72.4 (C-2′), 74.9 (C-3′), 76.7 (C-5′), 103.2 (C-1′), 126.4 (C-1), 137.7 (C-2), 168.8 (C-4). LR-MS (ES+) m/z requires 315.3, found 315.1 (M + Na+).
C); δC: (100.62 MHz; decoupled 1H 500 MHz; D2O) 18.4 (C-3), 62.5 (C-6′), 65.3 (C-5), 68.5 (C-6), 70.3 (C-4′), 72.4 (C-2′), 74.9 (C-3′), 76.7 (C-5′), 103.2 (C-1′), 126.4 (C-1), 137.7 (C-2), 168.8 (C-4). LR-MS (ES+) m/z requires 315.3, found 315.1 (M + Na+).
δ H (500 MHz, D2O) 0.61–1.50 (3H, br, m CH3–C), 1.53–2.41 (2H, br, backbone CH2), 3.37–3.62, 3.62–3.72, 3.72–3.86, 3.86–4.02, 4.02–4.16, 4.16–4.36 (10H, protons of carbohydrate and methylene side chain), 4.44 (1H, br, anomeric proton), 7.52 (Hmeta, arom.), 7.70 (Hpara, arom.), 7.99 (Hortho, arom). Aromatic resonances from terminal dithiobenzoate moiety.
3.3 Analysis
NMR spectra were recorded using a Varian Inova 500 spectrometer at 499.87 (1H) and 125.67 MHz (13C, 1H decoupled at 500 MHz) or using a Bruker Avance 400 spectrometer at 400.13 MHz (1H) or 100.26 MHz (13C, 1H decoupled at 400 MHz). NMR spectra were analyzed using the Varian VNMR 6.1C or MestRe Nova 5.2 software. IR spectra were recorded on a Perkin-Elmer 1600 Series FT-IR spectrometer by casting a film on NaCl plates from either DCM or MeOH. Mass spectra were acquired using a Micromass LCT spectrometer using ES+ ionization. Elemental analyses were obtained using an Exeter Analytical Inc. E-440 Elemental Analyzer. Aqueous SEC was performed using a Viscotek TDA 301 SEC system fitted with two (300 × 7.5 mm) TSKgel GMPWxl columns (Tosoh Biosciences) and differential refractive index, viscometry and right-angle light-scattering detectors. The eluent was 0.2 M NaNO3 and 0.1M NaH2PO4 in UHQ water at a flow rate of 1.0 mL min−1 and a constant temperature of 30 °C. Calibration for detector response was achieved using a single narrow PEO standard (Polymer Labs) with Mp 82,500 g mol−1 and a dn/dc value of 0.133 mL g−1. A dn/dc value of 0.153 mL g−1 for poly[2-(β-D-galactosyloxy)ethyl methacrylate] was determined from the RI detector response after injection of samples of known concentration. Values of Mn, Mw/Mn and Dh were determined using Viscotek Omnisec 4.0 for Windows software.3.4 Dynamic light-scattering
Polymeric ligands were prepared as 100 μM solutions in either phosphate-buffered saline (10 mM phosphate buffer pH 7.8, 137 mM NaCl, 2.7 mM KCl) or HEPES-buffered saline (10 mM HEPES buffer pH 7.8, 150 mM NaCl) and allowed to equilbrate at room temperature for 16 h. Dynamic light-scattering was performed using a Viscotek 802 instrument fitted with a 50 mW 830 nm laser and detection angle of 90°. Laser power was adjusted to ensure a mean count rate of at least 300 kilocounts per second and 10 experiments of 3 s were recorded. Experimental correlation functions were fitted with Viscotek OmniSIZE 3.0 and hydrodynamic radii calculated via the Stokes–Einstein equation. Mass and number distributions were calculated using the Dextrans mass model within the software.3.5 Isothermal titration calorimetry
Isothermal titration calorimetry was conducted using a MicroCal VP-ITC calorimeter equilibrated at 298 K. Ligands for analysis were prepared as 100 μM solutions in aqueous buffer (10 mM phosphate buffer pH 7.8, 137 mM NaCl, 2.7 mM KCl) and allowed to equilibrate for 24 h before degassing at 297 K. RCA120 was buffer exchanged by use of centrifugal size exclusion columns (Pierce Zeba Desalting Columns) prewashed with the same buffer. After buffer exchange RCA120 was further diluted in the same buffer and its concentration measured by UV absorption using an A1% value of 15.7 at 280 nm.19RCA120 showed some solution instability and subsequently, prior to each experiment, the stock solution was centrifuged to remove aggregated protein and the concentration redetermined. The lectin solution was added to the sample cell ensuring no trapped air bubbles and the mixture was equilibrated to 298 K. Ligand solutions were added to RCA120 as a series of injections (25 aliquots of 5 μL) at 3 min. intervals by means of a computer controlled syringe with constant stirring at 307 rpm. To control for ligand dilution effects the experiments were repeated in the absence of RCA120 and the resulting heats subtracted during analysis. Data were analysed using Origin 7.0 Pro (OriginLab) and fitted using the “single set of sites” model incorporated into the software.| Xb(i) = [Q(i)/ΔH·V] + Xb(i − 1) | (1) |
| Xf(i) = Xt(i) − Xb(i) | (2) |
In a normal Scatchard analysis, the average number of ligands bound per lectin (r(i)) is the ratio Xb(i)/Mt(i). The modified Scatchard analysis introduces an additional term to allow for multivalent ligands and thus:
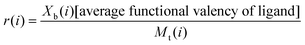 | (3) |
3.6 Surface plasmon resonance
All SPR measurements were performed on a BIAcore 3000 system and RCA120 was immobilised using a standard amino-coupling protocol. A CM5 sensor chip was equilibrated with HEPES buffer (10 mM HEPES pH 7.4, 150 mM NaCl, 0.005% P20 surfactant) then activated by flowing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 0.1 M N-hydroxysuccinimide and 0.1 M N-ethyl-N′-(dimethylaminopropyl)carbodiimide over the chip for 5 min at 25 °C at a flow rate of 5 μL min−1. RCA120 was immobilised on channels 1, 2 and 3 via injection of a solution (10 μg mL−1 in 10 mM acetate buffer pH 4) for 7, 3 and 1 min. respectively resulting in functionalisation of the surface at 5000, 2000 and 200 response units (RU) respectively. All channels were subsequently modified by flowing a solution of ethanolamine (1 M pH 8.5) for 10 min at 5 μL min−1 to produce a blank on channel 4 and remove remaining reactive groups on channels 1–3.
1 mixture of 0.1 M N-hydroxysuccinimide and 0.1 M N-ethyl-N′-(dimethylaminopropyl)carbodiimide over the chip for 5 min at 25 °C at a flow rate of 5 μL min−1. RCA120 was immobilised on channels 1, 2 and 3 via injection of a solution (10 μg mL−1 in 10 mM acetate buffer pH 4) for 7, 3 and 1 min. respectively resulting in functionalisation of the surface at 5000, 2000 and 200 response units (RU) respectively. All channels were subsequently modified by flowing a solution of ethanolamine (1 M pH 8.5) for 10 min at 5 μL min−1 to produce a blank on channel 4 and remove remaining reactive groups on channels 1–3.
Polymer solutions (500 pM–10 mM) were prepared in the same HEPES buffer. Sensorgrams for each polymer concentration were recorded with a 180 s injection of polymer solution (on period) followed by 240 s of buffer alone (off period). After this time the chip was regenerated by a 30 s injection of methylβ-D-galactoside (1 mg mL−1) and 60 s of buffer alone. After regeneration was complete the next sample was injected. For each polymer 5 consecutive concentrations were used for kinetic analysis using a single set of sites (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Langmuir Binding) model in the BIAevalulation 4.1 software.
1 Langmuir Binding) model in the BIAevalulation 4.1 software.
4 Conclusions
Although many studies on the binding of glycopolymers to lectins have been published (vide supra) few have studied the underlying thermodynamics and mechanism(s) of the interactions. Here we have studied the interaction between mono- and polyvalent galactosides synthesised from 2-(β-D-galactosyloxy)ethyl methacrylate and the lectin Ricinus communis agglutinin 120 by both isothermal titration calorimetry and surface plasmon resonance. As expected, avidities were greatly enhanced via multivalency with more than 4000-fold increase in Ka for the largest (highest valency) ligand by ITC equivalent to a 22-fold increase on a per-sugar basis. The combined ITC and SPR data suggest that the cluster glycoside effect between glycopolymeric ligands and lectins is the product of both chelation and “bind and slide” mechanisms.References
- M. Ambrosi, N. R. Cameron and B. G. Davis, Org. Biomol. Chem., 2005, 3, 1593–1608 RSC.
- N. Yamazaki, S. Kojima, N. V. Bovin, S. Andre, S. Gabius and H. J. Gabius, Adv. Drug Delivery Rev., 2000, 43, 225–244 CrossRef CAS.
- Y. Lee, R. Townsend, M. Hardy, J. Lonngren, J. Arnarp, M. Haraldsson and H. Lonn, J. Biol. Chem., 1983, 258, 199–202 CAS.
- Y. C. Lee and R. T. Lee, Acc. Chem. Res., 1995, 28, 321–327 CrossRef CAS.
- J. J. Lundquist and E. J. Toone, Chem. Rev., 2002, 102, 555–578 CrossRef CAS.
- M. Kanai, K. H. Mortell and L. L. Kiessling, J. Am. Chem. Soc., 1997, 119, 9931–9932 CrossRef CAS.
- T. K. Dam and C. F. Brewer, Biochemistry, 2008, 47, 8470–8476 CrossRef CAS.
- S. G. Spain and N. R. Cameron, Polym. Chem., 2011, 2, 60–68 RSC.
- V. Ladmiral, E. Melia and D. M. Haddleton, Eur. Polym. J., 2004, 40, 431–449 CrossRef CAS.
- S. G. Spain, M. I. Gibson and N. R. Cameron, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 2059–2072 CrossRef CAS.
- S. R. S. Ting, G. Chen and M. H. Stenzel, Polym. Chem., 2010, 1, 1392–1412 RSC.
- S. G. Spain, L. Albertin and N. R. Cameron, Chem. Commun., 2006, 4198–4200 RSC.
- N. R. Cameron, S. G. Spain, J. A. Kingham, S. Weck, L. Albertin, C. A. Barker, G. Battaglia, T. Smart and A. Blanazs, Faraday Discuss., 2008, 139, 359–368 RSC.
- S. Deng, U. Gangadharmath and C.-W. Chang, J. Org. Chem., 2006, 71, 5179–5185 CrossRef CAS.
- J. Adam, M. Pokorná, C. Sabin, E. P. Mitchell, A. Imberty and M. Wimmerová, BMC Struct. Biol., 2007, 7, 36 CrossRef.
- M. Ambrosi, N. R. Cameron, B. G. Davis and S. Stolnik, Org. Biomol. Chem., 2005, 3, 1476–1480 RSC.
- K. M. Halkes, A. C.d. Souza, C. E. P. Maljaars, G. J. Gerwig and J. P. Kamerling, Eur. J. Org. Chem., 2005, 3650–3659 CrossRef CAS.
- T. Wiseman, S. Williston, J. F. Brandts and L.-N. Lin, Anal. Biochem., 1989, 179, 131–137 CrossRef CAS.
- S. Sharma, S. Bharadwaj, A. Surolia and S. K. Podder, Biochem. J., 1998, 333, 539–542 CAS.
- T. K. Dam, R. Roy, D. Pagé and C. F. Brewer, Biochemistry, 2002, 41, 1351–1358 CrossRef CAS.
- T. K. Dam, H.-J. Gabius, S. André, H. Kaltner, M. Lensch and C. F. Brewer, Biochemistry, 2005, 44, 12564–12571 CrossRef CAS.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef.
- P. I. Kitov and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 16271–16284 CrossRef CAS.
- D. K. Mandal, N. Kishore and C. F. Brewer, Biochemistry, 1994, 33, 1149–1156 CrossRef CAS.
- S. A. Bernhard, J. Biol. Chem., 1956, 218, 961–969 CAS.
- Y.-Z. Liang, Z.-C. Li and F.-M. Li, J. Colloid Interface Sci., 2000, 224, 84–90 CrossRef CAS.
- T. K. Dam, R. Roy, S. K. Das, S. Oscarson and C. F. Brewer, J. Biol. Chem., 2000, 275, 14223–14230 CrossRef CAS.
- Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/.
- A. Herráez, Biochem. Mol. Biol. Educ., 2006, 34, 255–261 CrossRef CAS.
- A. G. Gabdoulkhakov, Y. Savochkina, N. Konareva, R. Krauspenhaar, S. Stoeva, S. V. Nikonov, W. Voelter, C. Betzel and A. M. Mikhailov, PDB ID: 1RZO, 2004.
- D. A. Mann, M. Kanai, D. J. Maly and L. L. Kiessling, J. Am. Chem. Soc., 1998, 120, 10575–10582 CrossRef CAS.
- H. Uzawa, H. Ito, P. Neri, H. Mri and Y. Nishida, ChemBioChem, 2007, 8, 2117–2124 CrossRef CAS.
- J. Geng, G. Mantovani, L. Tao, J. Nicolas, G. Chen, R. Wallis, D. A. Mitchell, R. G. Johnson, S. D. B. Evans and D. M. Haddleton, J. Am. Chem. Soc., 2007, 129, 15156–15163 CrossRef CAS.
- L. Yu, M. Huang, P. G. Wnag and X. Zeng, Anal. Chem., 2007, 79, 8979–8986 CrossRef CAS.
- C. R. Becer, M. I. Gibson, J. Geng, R. Ilyas, R. Wallis, D. A. Mitchell and D. M. Haddleton, J. Am. Chem. Soc., 2010, 132, 15130–15132 CrossRef CAS.
- T. K. Dam, T. A. Herken, B. S. Cavada, K. S. Nascimento, T. R. Moura and C. F. Brewer, J. Biol. Chem., 2007, 282, 28256–28263 CrossRef CAS.
- A. Alexeev, R. Verberg and A. C. Balazs, Phys. Rev. Lett., 2006, 96, 148103 CrossRef.
- A. Alexeev, R. Verberg and A. C. Balazs, Langmuir, 2007, 23, 983–987 CrossRef CAS.
- C. Dong, J. Cao, E. J. Struble and H. H. Lipowsky, Ann. Biomed. Eng., 1999, 27, 298–312 CrossRef CAS.
- E. F. Krasik and D. A. Hammer, Biophys. J., 2004, 87, 2912–2930 CrossRef.
- S. H. Thang, B. K. Chong, R. T. A. Mayadunne, G. Moad and E. Rizzardo, Tetrahedron Lett., 1999, 40, 2435–2438 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available: Solution size distributions of polymeric ligands by dynamic light-scattering. See DOI: 10.1039/c1py00030f/ |
| This journal is © The Royal Society of Chemistry 2011 |

