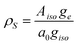Dinitrogen complexation with main group radicals†
Dennis
Kurzbach
ab,
Ajay
Sharma
ac,
Daniel
Sebastiani
ad,
Karl W.
Klinkhammer
b and
Dariush
Hinderberger
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128, Mainz, Germany. E-mail: dariush.hinderberger@mpip-mainz.mpg.de
bJohannes Gutenberg - University Mainz, Institute for Analytical and Inorganic Chemistry, Duesbergweg 10-14, 55099, Mainz, Germany
cDepartment of Chemistry, Northwestern University, Evanston, IL, USA
dDepartment of Physics, Freie Universität Berlin, Arnimallee 14, 14195, Berlin, Germany
First published on 25th November 2010
Abstract
In this report we present data from hyperfine sublevel correlation spectroscopy (HYSCORE), an electron paramagnetic resonance (EPR) spectroscopic technique, that reveals weak but distinct interactions between several main group element radicals and physically dissolved dinitrogen in solution. These interactions are the basis for a well-defined coordination of N2 to the paramagnetic centers. The complexes formed are primarily of the van der Waals-type but also feature a non-negligible orbital overlap between dinitrogen and the radicals' SOMO. Our spectroscopic findings are strongly supported by experiments with isotope-labeled 15N2, spectral simulations and quantum chemical and density functional theory (DFT) calculations. Formation of such complexes is unexpected when considering the small polarizability of dinitrogen but steric effects like formation of a binding “pocket” may facilitate their formation. The sensitivity, selectivity, and resolution of HYSCORE with respect to the detection of weak hyperfine couplings is needed to identify such complexes that are probably the result of a subtle interplay of induced van der Waals forces between N2, the solvent and the dissolved radicals.
Introduction
Since the first discovery of a dinitrogen complex ([Ru(NH3)5(N2)]2+) in 19651 the field of dinitrogen coordination and activation was focused on complex compounds of transition metals2–4 and bare main group metals.5,6 These metal–N2 complexes feature strong interactions with dinitrogen. Furthermore, weak complexes between small gas molecules are well known and documented in the literature,7 also for nitrogen.8 Complexes to larger radicals in solution, however, have to our knowledge, not been documented before, with the exception of the decomposition of azo-compounds. This chemical process can involve a transition state in which N2 is trapped in a solvent cage with two organic radicals, directly after thermally or photochemically triggered decomposition.9Among the methods of physical characterization of strong, metal-based complexes, electron paramagnetic resonance (EPR) spectroscopy has been applied successfully to determine electronic ground states and molecular geometries of several complexes.10–12
Going beyond the structure of the paramagnetic center, with sophisticated pulse EPR methods one can also probe the chemical or rather magnetic environment. These methods are pulse electron nuclear double resonance (ENDOR) and hyperfine sublevel correlation (HYSCORE) spectroscopy, which allow measuring hyperfine couplings from the unpaired electron spin to surrounding magnetically active nuclei.13–15 As these experiments are performed in frozen solution (as in this report) or in solids, from the anisotropies and orientation dependence (if it is resolved) of the hyperfine coupling one can obtain valuable information on the geometric structure up to ∼1 nm around the radical center. In our collaborative research effort, we have characterized the structure and dynamics of the recently synthesized persistent radicals of the heavy main group elements tin and lead, mainly based on EPR spectroscopy and X-ray crystallography.16 In the course of these investigations, we performed HYSCORE experiments on the SnHyp3 radical16 (Hyp = Si(SiMe3)3, see Fig. 1) to study the magnetic nuclei surrounding the central electron spin via measurements of intramolecular hyperfine interactions.13 Here, we report the results of these HYSCORE experiments, which revealed surprising, distinct hyperfine couplings of the radical and N2. With a series of experiments, using isotope-labeled 15N2, gas exchange to Ar atmosphere, and even different radicals in different solvents, we were able to trace back these hyperfine couplings to the formation of weak van der Waals complexes of dinitrogen with the paramagnetic main group compounds.
 | ||
| Fig. 1 a) The molecular structure of the SnHyp3 compound and the definition of the molecular coordination frame. As the central tin is to first approximation planar coordinated by the hypersilyl ligands, one can simplify the plane spanned by them to the x/y plane. b) The molecular structure of the used triarylmethyl radical (TAM). | ||
Results
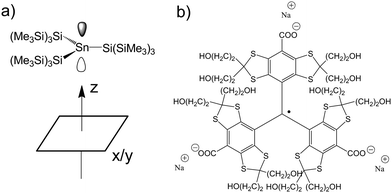
Fig. 2 depicts the low-temperature, electron-spin-echo-detected EPR spectrum a) and the HYSCORE spectra b), c)–f) of SnHyp3 in pentane saturated with either nitrogen or argon.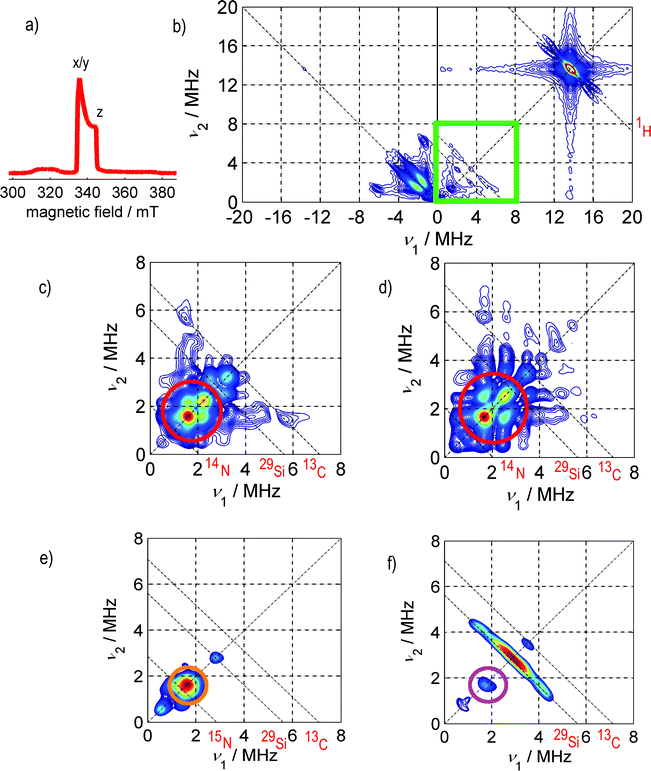 | ||
| Fig. 2 a) Electron spin echo (ESE)-detected spectrum of SnHyp3. The relevant field positions for the HYSCORE experiments are marked with x/y for the field position correlated with the orientation of the ligand plane and with z for the orientation of the p-like singly occupied molecular orbital (SOMO) of SnHyp3 (See Fig. 1 for the geometry of the molecular framework). Note that the ESE-detected spectra of SnHyp3 in pentane under Ar and N2 atmosphere were identical. b) The full HYSCORE spectrum in the x/y direction in pentane saturated with argon. The signal marked 1H can be ascribed to intramolecular couplings of the unpaired electron to the methyl groups of the ligands. The ridges on the left side, in the (−,+)-quadrant can be assigned to intramolecular or solvent–radical hyperfine interactions, but are not yet completely understood. c) Shows the frequency range marked with the green square in b), for the case of nitrogen saturated pentane. All HYSCORE data in Ar and N2 atmosphere were identical with the exception of the marked region in all experiments. Here, the HYSCORE spectrum in nitrogen saturated pentane in the x/y direction is shown. The red circle marks an additional coupling to a nitrogen nucleus. Hence, only this region (0–8 MHz) is presented in the following. d) The HYSCORE spectrum in nitrogen saturated pentane along the z direction. e) The spectrum in z-direction in pentane saturated with 15N2. One detects a strong coupling (marked orange) appearing slightly, yet clearly above the resonance frequency of 15N. Due to the missing quadrupolar coupling to 15N (I = 1/2 instead of I = 1 for 14N), this signal is shaped much simpler than the 14N one. f) SnHyp3spectrum in Ar-saturated pentane. Note, that in the case of argon saturation, the spectrum of the z direction does not differ significantly from the x/y one and is therefore not presented. The purple circle marks hyperfine couplings assigned to residual N2 in the sample (the so-called “matrix peak”). The ridges marked 29Si and 13C are due to intramolecular coupling of the unpaired electron to silica or carbon nuclei contained in the hypersilyl ligands. The intensive ridges on the left side of the spectra are present and unchanged in all samples regardless of the atmosphere. They probably stem from intramolecular hyperfine couplings to 29Si nuclei of the ligand sphere. The red element symbols mark the resonance frequencies of the respective nuclei which are indicated by dashed anti-diagonal lines. | ||
All HYSCORE data in Ar and N2 atmosphere were identical with the exception of the region marked by red circles in all experiments. Hence, only this region (0–8 MHz) is presented in the following. Obviously, a weak coupling pattern appears in the case of nitrogen saturation (marked by red circles), that is not present in the argon case. Spectral simulations, based on the ZOMA program package14 confirmed that the coupling can be traced back to hyperfine and quadrupole couplings of at least one nitrogen nucleus (I = 1). The spectral simulations shown in Fig. 3 were performed using an isotropic hyperfine coupling with tensor elements [Axx, Ayy, Azz] = [0.3, 0.3, 0.3] MHz, a quadrupolar coupling of |e2qQ/h| = −0.3 MHz and a Q-tensor asymmetry of η = 0.4. (The nuclear quadrupole interaction is κ = e2qQ/(h4I(2I − 1)) and the asymmetry parameters η = (Qx − Qy)/Qz with Qx = −κ(1 − η), Qy = −κ(1 + η), and Qz = 2κ).
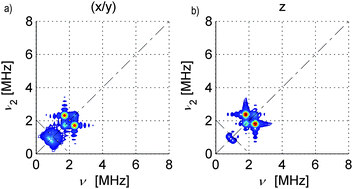 | ||
| Fig. 3 Simulated 14N HYSCORE spectra for SnHyp3: a) along the molecular x/y direction and b) along the z direction. The simulations were calculated with a perfect S/N ratio and the ridges at approx. 1 MHz look more intense than in the measured spectra. Also, the signal marked purple in Fig. 2f) was not considered during the simulation. | ||
A closer look at Fig. 2c) and d), though, illustrates that there is a minimal anisotropy, namely a slightly stronger coupling along the molecular z direction (see Fig. 1a) for an illustration of this direction in the molecular frame).
Furthermore, for SnHyp3 the spin density distribution onto the 14N nucleus could be calculated from the isotropic hyperfine couplings as 0.016% of the overall spin density (for details see the Methods section).16
Experiments with isotope-labeling—15N2
To ensure the correctness of the above interpretation, we detected spectra with 15N2 saturated pentane instead of 14N2 (Fig. 2e)). In this case, one detects a strong peak 0.2 MHz above the resonance frequency of 15N superimposed with a 15N matrix signal. Since 15N (I = 1/2) lacks a quadrupolar moment, a much simpler spectrum than that in Fig. 2d) appears. Assuming a matrix peak and an A-tensor of [0.8, 0.8, −2.1] MHz with orientation angles [−30, −64, 0]° relative to the framework defined in Fig. 1, the spectrum in Fig. 2d) can be simulated nicely (see Fig. S3 in the Supporting Information and Fig. S2 for the spectrum in x/y direction; note that the orientation of the A-frame is not connected to the spatial orientation of N2†). This fits well with the expectations one infers from the 14N data: a stronger interaction from z-direction and a certain isotropic contribution due to orbital overlap. The differences in coupling strength between the 14N and the 15N case should scale with the ratio of the magnetogyric ratios (γ(14N)/γ(15N) = |0.404/−0.566|). Taking into account that the quadrupolar moment dominates the spectrum in the 14N case and the dipolar interaction in the 15N case, which complicates analysis, the simulated A-values are in relatively good agreement.Note that the marked peak in Fig. 2f) could easily be mistaken for the 15N peak in Fig. 2e) since the difference in resonance frequency is only 0.05 MHz (at the same field position), but shape and intensity differ significantly. Having shown the principle agreement of 15N and 14N measurements, we will in the following, only discuss the 14N-derived spectra. Due to their much stronger and characteristic coupling patterns from quadrupolar contributions, detection and discussion is tremendously simplified.
It should be noted that coupling patterns as seen in Fig. 2c)–2e) were not observed when tetrahydrofuran (THF) was used as solvent.
Variation of gas atmosphere
To check for possible effects of the concentration of physically dissolved gas on the spectra, the HYSCORE experiments with SnHyp3 dissolved in pentane were repeated in an atmosphere of equimolar argon and nitrogen (the solubility of argon and nitrogen in pentane is nearly identical17). These experiments yielded exactly the same coupling pattern as the case of using 100% N2 with only slight changes in the relative intensity of the nitrogen signals (spectra are shown in Figures S10 and S11 in the Supporting Information†). From these spectra, one can infer that the same kind of complex is formed as in the presence of 100% nitrogen, just by a smaller number of radicals. The complexation energy may therefore not (or only slightly) depend on the amount of dissolved N2. However, further investigations with variation of the atmosphere are necessary which may help in quantifying the binding energy.Variation of radicals
To test whether the coupling appearing under nitrogen atmosphere is specific for the heavy main group element radical SnHyp3 or can also be observed with other radicals, we studied radicals of lighter group 14 elements. A carbon based triarylmethyl radical (TAM, see Fig. 1 for the detailed structure) was used and examined with HYSCORE. Also this compound, dissolved in nitrogen-saturated methanol (TAM can only be dissolved in polar solvents), displays a hyperfine coupling pattern that can be attributed to nitrogen nuclei (for the detected spectra and spectral simulations, see Figures S4–S7 in the Supporting Information†). When the same solution is prepared under argon, no such hyperfine interaction pattern could be detected. In this case, the spectral simulations of the nitrogen pattern revealed a clearly anisotropic A-tensor of A = [0.05, 0.05, 0.15] MHz, a quadrupolar coupling strength of |e2qQ/h| = 3.2 MHz and a quadrupolar asymmetry of η = 0.5.Apparently, the specific hyperfine coupling to N2 is observable in light (carbon-based) and heavy (tin-based) radicals with comparable, almost planar molecular geometries. In both of these radicals the SOMO is a pz-type orbital. To further assess whether this coupling can in general also be observed in HYSCORE spectra of radicals based on different SOMO, we investigated the nitroxide-based radical TEMPOL (2,2,6,6-tetramethylpiperidine-1-oxyl) in methanol. The TEMPOL SOMO is an antibonding π*-orbital.18 Again a coupling pattern could be observed when the solution was prepared under nitrogen that did not appear when the solution was prepared under argon. The main difference in the HYSCORE spectra of SnHyp3 or TAM and those of TEMPOL is that the 14N coupling strength for the latter (again as found from spectral simulations) was considerably stronger and therefore appeared in the (−,+)-quadrant. (For the spectra, see the Supporting Information†).
Quantum chemical and density functional theory calculations
To complement these experimental observations, we have performed quantum chemical calculations on the structure and properties of the isolated SnHyp3 molecule and a proposed complex with N2. The molecular structure was optimized within density functional theory, yielding a slightly non-planar SnSi3 scaffold (in the absence of N2). This calculated structure perfectly matches the solid-state structure determined by X-ray crystallography and data from previous EPR studies.16 Note that the deviation from planarity is only small and therefore its orientation is not expected to be static but should repeatedly invert at finite temperature.To estimate the strength of van der Waals interactions between SnHyp3 and N2, we have performed total energy calculations on the Møller–Plesset perturbation level of theory (MP2, see Methods), inserting an N2 molecule along the C3 symmetry axis from the side which is less sterically hindered by the presence of the SiMe3 groups. To ease the calculations, we simplified the molecule by replacing some of the SiMe3 groups by simple methyl groups. The counterpoise-corrected MP2 interaction energy was found to be about 1 kcal mol−1, at an equilibrium distance between the Sn atom and the N2 molecule of 5.0 Å (the interaction energy vs. distance is shown in Figure S12 in the Supporting Information†). While this represents a rather weak interaction energy, it might nevertheless be sufficient to enable a certain clustering of SnHyp3 and N2. Furthermore, cage effects could contribute to the stabilization of these complexes (see next section). Note that a Mulliken charge population analysis for SnHyp3 revealed an (integrated) unpaired spin density of 0.02 × 10−2 elementary charges on the 14N nucleus. This is in remarkable agreement with the spectroscopically (through the hyperfine coupling) determined spin population of 0.016%.
As a complementary aspect, the unpaired electronic spin density distribution was computed at the level of unrestricted density functional theory, using the BLYP exchange–correlation functional. This density is shown in Fig. 4. It is apparent that the spin density is highly delocalized, and not restricted to the region around the Sn center. Both the Sn–Si bonds and some of the Si–Si bonds exhibit a certain spin polarization. The shape of the out-of-plane spin density is strongly asymmetric, which is due to the slightly non-planar SnSi3 scaffold. Although the spin density appears more localized in the more open region (from which we have inserted the N2), its spatial extent ranges a bit further out, i.e. its numerical value is somewhat larger towards the guest N2 than in the opposite direction. Remarkably, we find a considerable amount of spin density directly on top of one of the nitrogen atoms.
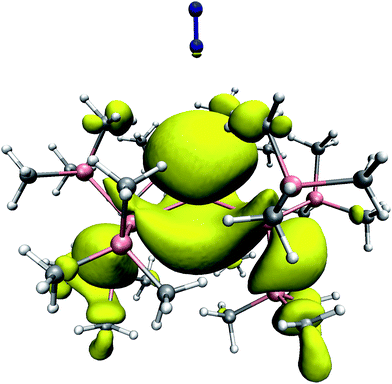 | ||
| Fig. 4 The unpaired electron spin density distribution in SnHyp3 with N2 placed along the molecular z axis, as derived from DFT calculations. The isosurface was taken at a spin density value of 0.001 e Å−3, which corresponds to 0.6% of the maximum value reached in the entire complex. Color code: H: white; C: grey; Si: magenta; N: blue. | ||
Discussion
From the couplings marked red and orange in Fig. 2c), d), e), and the spectral simulations in Fig. 3 we can clearly state that there is a significant, detectable hyperfine/quadrupolar interaction between the radical centers and physically dissolved N2 in the solution. This is due to the fact that other factors could be excluded experimentally, so that the only source for the appearance or disappearance of the strong signal in Fig. 2c)–f), was the used gas atmosphere.From the experimental point of view, the question remains whether this is a coupling of the SnHyp3 radical to statistically distributed N2 in the solution or a coupling due to an interaction of van der Waals nature, as it was found in the MP2-type calculations.
The possibility of a dipolar (acting solely through space) coupling to dinitrogen distributed statistically in the solution was plausible as the solubility of N2 in pentane is in the range of the radical concentration (10–50 mmol) used.19 Even without deeper spectral analysis by simulation of the HYSCORE spectra, the observed phenomenon qualitatively has the character of an “on/off” experiment: The appearance of the coupling in Fig. 2c), d) and e) was solely dependent on the gas dissolved in the solution. The residual possibility of impurities from the synthesis of the tin centered radical as cause for the coupling was further excluded by intensively purifying the solvent and spectroscopic and crystallographic analysis of the used compounds.
From the hyperfine/quadrupolar coupling pattern that can be nicely reproduced in spectral simulation, a weak but specific coupling of the radical center to N2 can be postulated as it is also found in the MP2 calculations. The fact that the interaction in Fig. 2c), d) and e) is anisotropic but has a small, but non-negligible isotropic contribution is quite remarkable and cannot be trivially explained. It is reasonable to assign the molecular arrangement underlying the measured couplings to be of coordinative nature, possibly as a pure van der Waals-type (multipole-induced dipole) complex between the studied radicals and dinitrogen. In the context of a van der Waals interaction, two experimental findings are surprising: the non-negligible isotropic contribution and the sharp appearance of the coupling pattern. The isotropic hyperfine coupling contribution is very small but as HYSCORE is a very sensitive method to detect weak hyperfine couplings, it is nonetheless spectroscopically indicative of orbital overlap between Sn and the closer nitrogen atom of N2, giving way to unpaired electron spin density in s-type orbitals of this nitrogen. A loosely bound van der Waals complex should lead to a rather large structural variety in the position of N2 relative to the radical center and would hence yield a broad distribution of couplings. This broad distribution would appear as strongly blurred ridges in the HYSCORE spectra, which is clearly not observed.
All these conclusions on the geometric and electronic structure of our system can be nicely explained when assuming a weak but specific van der Waals complex of SnHyp3 and N2 and unpaired electron spin density transfer from Sn to N2. This is also in excellent agreement with the findings from our quantum chemical calculations. The numerical value of about 1 kcal mol−1 for the optimized attractive energy between the two molecules is typical for a pure van der Waals interaction. Remarkably, the assumed spin density delocalization from Sn onto the first nitrogen of N2 that is found in the HYSCORE data qualitatively manifests itself in the DFT calculations as well.
It should be noted that we trap the van der Waals complex by freeze-quenching the sample at the glass transition temperature of the solution. As the attractive energy is weak, the van der Waals complexes can be assumed to have a short lifetime and to continuously form and dissociate at ambient temperature. Nonetheless, our HYSCORE results suggest that at any given moment of time, a large fraction of the radicals partake in these van der Waals complexes even at moderate temperatures.
Although weak complexes between small gases are well documented,7,8 complexes to larger radicals in solution however, have to our knowledge, not been documented before, except for transition states after decomposition of azo-compounds.9 These so called cage effects have been subject to many investigations, but spectroscopic evidence for a weak binding interaction between N2 and surrounding radicals, to our knowledge, has not been published so far. Some points can be concluded from the mentioned studies: first, the stability of a N2 2R˙ cage is basically dependent on the viscosity of the solvent and the thermal energy contributing to the diffusion rate of the radicals (also by decreasing the solvent viscosity).20 In our case the solvent viscosity of pentane is relatively low, but a snap shot of the situation at the glass transition temperature is detected by our measurements. This temperature (for pentane ∼150 K) is clearly below the average temperature used for studying the decomposition of azo-compounds. Therefore, the possibility of a solvent cage stabilizing the detected N2 complex should be taken into account.
Second, it is proposed that a good solvation of produced radicals after the azo-decomposition reduces cage effects.21 This corresponds nicely with our finding that coordination to any of the used gases cannot be detected in THF, since THF can most likely stabilize the SOMO by electron donation. From these two arguments, a contribution of cage effects to the stability of our proposed radical–N2 complexes seems even more likely. The actual overall stabilization energy could therefore exceed the quantum mechanically calculated of 1 kcal mol−1.
However, the literature has focused on transition states. Cages including N2 and main group radicals, though strong enough to lead to recombination effects, are elusive in the case of azo-compounds. Positive interaction between N2 and radicals produced by decomposition of such compounds has, to our knowledge, not been published yet, but in our case, the positive interaction between the radical and N2 is strong enough to stabilize a possible “in-cage situation” over time.
Furthermore, the HYSCORE spectra can be simulated with a coupling to only one 14N (or 15N, respectively). Hence, one can infer that physical coordination to the tin radical takes place via only one of the nitrogen nuclei in N2. From this fact it is suggestive that the nitrogen is coordinated “end-on” onto the central tin radical from the molecular z-direction (see Fig. 1 and 4). Coordination along this direction corresponds with one's intuition, since the only access towards the central atom is from the molecular z-direction (top or bottom, see Fig. 4) In principle, “side-on” coordination can be imagined, too, but besides the EPR-based conclusions, also our MP2 calculations support the “end-on” case. In these calculations, “side-on” complexes were not found to be energetically favorable.
The distance between the tin center and the first nitrogen nucleus as found from the MP2 calculations (∼5.2 Å) is also in good agreement with what can be expected from the hyperfine and quadrupolar coupling strength. With the weak attractive energy for the van der Waals complex found here, one has to discuss the relative interaction strengths between solvent molecules and N2, between solvent molecules and the radical, and between the radical and N2. In this context it is noteworthy that in THF solution, coordination of N2 to SnHyp3 could not be detected, which may suggest that THF displaces the dinitrogen molecule due to its donor character. This observation can be explained if one assumes that the interaction between solvent or dissolved dinitrogen and radical can be traced back to electron lone pairs on the respective solvent or N2. In THF, the THF–SnHyp3 interaction may dominate, while in pentane (without lone pairs) the weak attraction between the radical and N2 is not suppressed by the stronger interaction of radical and solvent. Although this question cannot be finally answered from the experimental and computational results in our study, it seems plausible that it must be electron-rich centers that coordinate to SnHyp3. Since the dinitrogen concentration is in the range of the radical concentration, one can also speculate that the attraction between N2 and pentane is at least slightly weaker than the N2–SnHyp3 attraction . Otherwise the small amount of N2 should be distributed uniformly in the solution, which can be excluded due to the sharp ridges observed in the HYSCORE spectra indicating a very specific geometry of the van der Waals complex.
When nitrogen and argon are dissolved in the pentane solution in equal amounts (see the Results Section and Figures S10 and S11 in the Supporting Information†), the unchanged spectral shape further supports the assignment of a specific albeit weak van der Waals complex of SnHyp3 and N2. If the nitrogen coupling observed in HYSCORE were of purely statistical nature, the coupling shape should be very sensitive to the amount of dissolved N2. This is clearly not the case in our spectra.
The increase in hyperfine and quadrupolar coupling anisotropy when using TAM instead of SnHyp3 as a radical, still supports the derived picture. Note that the solubility of N2 in methanol is slightly lower than the solubility in pentane,22 but did not lead to a qualitatively different phenomenon. Due to the stronger sterical shielding of the central carbon by the aryl groups when compared with the hypersilyl ligands surrounding the tin atom, the central atom becomes less accessible and thus the average coupling strength decreases. This explanation is mirrored in the fact that the coupling strength of dinitrogen to the nitroxide based TEMPOL radical in turn increases (see Figures S8 and S9 in the Supporting Information†). Altogether we are convinced that we have discovered a weak but specific van der Waals coordination of dinitrogen to several radical species with non-negligible orbital overlap. Whether diamagnetic main group element compounds are capable of forming such a van der Waals complex is a much more complicated question to answer since the specificity one has with EPR methods is restricted to radicals and the expected strength of the effect may not be strong enough to be observable with other physical methods. Furthermore, our findings illustrate the power of the highly sensitive and selective HYSCORE experiment to detect small hyperfine couplings that stem from such weak van der Waals complexes. The combination of an experimental EPR method such as HYSCORE with quantum chemical and DFT calculations yields the fingerprint of the formation of the van der Waals complex and the insight needed to semi-quantitatively understand this phenomenon. It is therefore not surprising that such a phenomenon concerning ubiquitous dinitrogen in solution has been reported here for the first time. Experiments with further, better polarizable gases than N2 are carried out in our lab at this time.
Methods
The tin species was dissolved in pentane, previously saturated with argon or nitrogen and subsequently transferred into EPR sample tubes (quartz glass, 3 mm outer diameter), in a glove box with nitrogen atmosphere or using standard Schlenk hardware flushed with argon. Samples saturated with a mixture of argon and pentane were prepared using modified Schlenk hardware, which were flushed with a mixture of argon and nitrogen. TAM and TEMPOL were dissolved in methanol as a solvent that was prepared exactly like pentane. Echo-detected, field-swept EPR spectra were recorded with a primary echo sequence (π/2)–τ–(π)–τ–echo while sweeping the magnetic field using a Bruker ELEXSYS 580 spectrometer with a Flexline split-ring resonator (ER 4118X-MS3, overcoupled to Q-values of typically 100). All experiments were performed in glassy, shock-frozen solution at X-band frequencies (∼9.4 GHz) at 8 K.HYSCORE experiments employed the pulse sequence π/2–τ–π/2–t1–π–t2–π/2–τ–echo. The following parameters were used: mW pulses of lengths tπ/2 = tπ = 16 ns, starting times 96 ns for t1 and t2, and time increments Δt = 16 ns (data matrix 256 × 256). Spectra with different τ values were recorded. An eight-step phase cycle was used to remove unwanted echoes. The HYSCORE data were processed with MATLAB 6.5 (The MathWorks, Inc.). The time traces were baseline corrected with an exponential, apodized with a Gaussian window and zero filled. After, two-dimensional Fourier transformation absolute-value spectra were calculated. Spectra recorded with different τ values were added to eliminate τ-dependent blind spots. HYSCORE spectra were simulated applying the MATLAB based ZOMA package.14
In all cases the temperature was set to 8 K by cooling with an ARS cryostat and closed-cycle cooling system. The samples were prepared as concentrated solutions (concentrations typically >10 mM) and the sample volume was always large enough to fill the complete resonator volume in the probehead (>300 μL).
The used chemical substances were commercially available or synthesized as reported earlier.16a
EPR Theory
The spin Hamiltonian for an S = ½ system coupled to i nuclei, in frequency units, is given by| H = (βe/h)SgB0 + ∑ SAiIi − (βn/h)∑ gi,nIiB0 + ∑ IiQiIi, | (S1) |
The hyperfine spectrum of a nucleus with spin I = 1/2 at a single orientation consists of two transitions. For B0 along one of the hyperfine principal axes the frequencies are given by 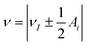 , where νI is the nuclear Zeeman frequency and Ai is one of the principal hyperfine values. A HYSCORE spectrum contains cross-peak between the nuclear frequencies in one electron spin manifold with the nuclear frequencies in the other electron spin manifold. Generally, only a few of all possible cross-peaks are observed.
, where νI is the nuclear Zeeman frequency and Ai is one of the principal hyperfine values. A HYSCORE spectrum contains cross-peak between the nuclear frequencies in one electron spin manifold with the nuclear frequencies in the other electron spin manifold. Generally, only a few of all possible cross-peaks are observed.
Spin density approximation
Assuming a perfect s-type orbital on the nitrogen nucleus to contain 100% of the spin density, the spin density distributed onto 14N in our case (ρs) was calculated by:Here, Aiso, is the experimental isotropic hyperfine coupling found in the HYSCORE experiments, a0 = 1809.36 MHz, is the hyperfine coupling constant for an s-orbital on a 14N nucleus containing 100% of the overall spin and giso = 2.0463.10
First-principles calculations
We have optimized the full SnHyp3 molecule within density functional theory (CPMD package, unrestricted BLYP exchange–correlation functional, Goedecker effective core potentials and a 60Ry plane wave cutoff) in order to plot the spin density (the difference between the densities of the α and β spin channels). For the calculation of the van der Waals interaction energy between SnHyp3 and an N2 molecule, we simplified the molecule by replacing six Si–(CH3)3 groups by methyls. The region from where the N2 is approached was left unchanged. The total energies were computed on the Møller–Plesset perturbation theory level (MP2), using the Stuttgart Relativistic Large Core effective core potentials for Sn and Si, combined with DZ/TZ basis sets.23 H, C and N atoms were assigned a 6-311G(2d,2p) basis. The N2 molecule was placed in the ‘end-on’ conformation at a series of distances between 4.8 and 5.5 Å from the Sn center for the (MP2-) calculation of the potential energy curve.Acknowledgements
The authors thank Christian Bauer for technical support, Prof. Katja Heinze for helpful discussions and Prof. Hans W. Spiess for continuing support. This work was financially supported by the Deutsche Forschungsgemeinschaft (DFG) under grants number HI 1094/2-1, Se 1008/5 and Se 1008/6.Notes and references
- A. D. Allen and C. V. Senoff, Chem. Commun., 1965, 24, 621 Search PubMed.
- J. Chatt, J. R. Dilworth and R. L. Richards, Chem. Rev., 1978, 78, 589 CrossRef CAS.
- M. Hidai and Y. Mizobe, Chem. Rev., 1995, 95, 1115 CrossRef CAS.
- M. D. Fryzuk and S. A. Johnson, Coord. Chem. Rev., 2000, 200–202, 379 CrossRef CAS; D. J. Knobloch, E. Lobkovsky and P. J. Chirik, Nat. Chem., 2009, 2, 30.
- H.-J. Himmel and N. Hebben, Chem.–Eur. J., 2005, 11, 4096 CrossRef CAS.
- H.-J. Himmel and M. Reiher, Angew. Chem., Int. Ed., 2006, 45, 6264 CrossRef CAS.
- R. E. Miller, Science, 1988, 240, 447 CrossRef CAS; R. C. Cohen and R. J. Saykally, J. Phys. Chem., 1992, 96, 1024 CrossRef CAS.
- C. Laush and J. M. Lisy, Chem. Phys. Lett., 1993, 210, 347 CrossRef CAS; R. W. Randall, T. R. Dyke and B. J. Howard, Faraday Discuss. Chem. Soc., 1988, 86, 21 RSC.
- G. S. Hammond, J. N. Sen and C. E. Boozer, J. Am. Chem. Soc., 1955, 77, 3244 CrossRef CAS; H. P. Waits and G. S. Hammond, J. Am. Chem. Soc., 1964, 86, 1964.
- E. Wasserman, L. Barash and W. A. Yager, J. Am. Chem. Soc., 1965, 87, 2075 CrossRef CAS.
- R. R. Lemke, R. F. Ferrante and W. Weltner Jr., J. Am. Chem. Soc., 1976, 99, 416.
- G. Maier, H. P. Reisenauer and J. Glatthaar, Organometallics, 2000, 19, 4775 CrossRef CAS.
- P. Höfer, A. Grupp, H. Nebenführ and M. Mehring, Chem. Phys. Lett., 1986, 132, 279 CrossRef.
- Z. Madi, S. van Dorslaaer and A. Schweiger, J. Magn. Reson., 2002, 154, 181 CrossRef CAS.
- A. Schweiger, G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press, 2001 Search PubMed.
- M. Becker, C. Förster, C. Franzen, J. Hartrath, E. Kirsten, J. Knuth, K. W. Klinkhammer, A. Sharma and D. Hinderberger, Inorg. Chem., 2008, 47, 9965 CrossRef CAS; C. Förster, K. W. Klinkhammer, B. Tumanskii, H.-J. Krüger and H. Kelm, Angew. Chem., 2007, 129, 1174 CrossRef; D. Kurzbach, S. Yao, D. Hinderberger and K. W. Klinkhammer, Dalton Trans., 2010, 39, 6449 RSC.
- W. L. Masterton, D. A. Robins and E. J. Solwinski Jr., J. Chem. Eng. Data, 1961, 6, 531 CrossRef CAS.
- I. Morishima, K. Yoshikawa and T. Yonezawa, Chem. Phys. Lett., 1972, 16, 336 CrossRef CAS; I. Novak, L. J. Harrison, B. Kovac and L. Pratt, J. Org. Chem., 2004, 69, 7628 CrossRef CAS.
- H. Kalra, D. B. Robinson and J. Besserer, J. Chem. Eng. Data, 1977, 22, 215 CrossRef CAS.
- C. Dell'Erba, A. Houmam, M. Novi, G. Petrillo and J. Pinson, J. Org. Chem., 1993, 58, 2670 CrossRef CAS; G. S. Hammond and J. R. Fox, J. Am. Chem. Soc., 1964, 86, 1918 CrossRef CAS.
- G. S. Hammond, C.-H. S. Wu, O. D. Trapp, J. Warkentin and R. T. Keys, J. Am. Chem. Soc., 1960, 82, 5394 CrossRef CAS; H. Torii, K. Fujimoto and H. Kawaguchi, J. Polym. Sci., Part A: Polym. Chem., 1996, 34, 1237 CrossRef CAS.
- R. Battino, T. R. Rettich and T. Tominaga, J. Phys. Chem. Ref. Data, 1984, 13, 563 CAS.
- W. Kuechle, M. Dolg, H. Stoll and H. Preuss, Mol. Phys., 1991, 74, 1245.
Footnote |
| † Electronic supplementary information (ESI) available: HYSCORE spectra of TAM in methanol, TEMPOL in methanol, SnHyp3 under Ar/N2 mixture and interaction energy plot Sn–centre/N2. See DOI: 10.1039/c0sc00345j |
| This journal is © The Royal Society of Chemistry 2011 |