Universal characteristics of chemical synthesis and property optimization†
Katharine W.
Moore
a,
Alexander
Pechen
a,
Xiao-Jiang
Feng
a,
Jason
Dominy
b,
Vincent
Beltrani
a and
Herschel
Rabitz
*a
aDepartment of Chemistry, Princeton University, Princeton, NJ 08544, USA. E-mail: hrabitz@princeton.edu
bProgram in Applied Mathematics, Princeton University, Princeton, NJ 08544, USA
First published on 21st January 2011
Abstract
A common goal in chemistry is to optimize a synthesis yield or the properties of a synthesis product by searching over a suitable set of variables (e.g., reagents, solvents, reaction temperature, etc.). Synthesis and property optimizations are regularly performed, yet simple reasoning implies that meeting these goals should be exceedingly difficult due to the large numbers of possible variable combinations that may be tested. This paper resolves this conundrum by showing that the explanation lies in the inherent attractive topology of the fitness landscape specifying the synthesis yield or property value as a function of the variables. Under simple physical assumptions, the landscape is shown to contain no suboptimal local extrema that could act as traps on the way to the optimal outcome. The literature contains broad evidence supporting this “OptiChem” theory. OptiChem theory implies that increasing the number of variables employed should result in more efficient and effective optimization, contrary to intuition.
1. Introduction
Two general goals in chemistry are to optimize synthesis yields and the properties of the products. With several hundred years of chemical experience to draw on, these optimization goals are consistently achieved for many different objectives. Synthesis and property optimization is widely successful even though there is no a priori reason to expect that optimization in chemistry should be easy, or even practically feasible. On the contrary, simple reasoning suggests that optimization in chemistry should be exceedingly difficult. Importantly, the notion of the observed “ease” of performing optimization in chemistry refers to considering the apparent mathematical complexity of the tasks, as explained below, and not to the often difficult and time consuming overhead of setting up and performing individual experiments.In a typical reaction optimization, the goal is to obtain the maximal product yield by changing a small number of suitable variables, such as the concentration of reagents and catalysts, the choice of solvent(s), reaction temperature, etc. In addition, when kinetics plays a role, the reaction time may also be a variable. Even when using chemical intuition to choose which values of the variables to sample, it may be expected that finding the absolute best values that maximize reaction yield should require testing the majority of their possible combinations. Typically, no more than ∼5–10 variables are chosen in order to avoid the “curse of dimensionality”,1 which states that the number of possible experiments (i.e., unique combinations of variable values) grows exponentially with the number of variables. The large number of possible independent experiments could render reaction optimization practically infeasible as the size of the pool of variables rises.
Contrary to the reasoning above, experience shows that synthesis and property optimizations in chemistry are far easier to achieve than the curse of dimensionality suggests. Furthermore, quantitative evidence for optimization being extremely efficient in chemistry comes from many areas. Typically, “smart” optimization methods such as factorial design,2 directed evolution,3,4 or genetic algorithms5 are used to find the best values of the variables. Efficient optimization has been observed in organic synthesis,6–8 discovery of functional proteins,9–26 optimization of catalytic activity,27–39 and the properties40–50 of materials. The typical numbers of variables and resulting possible experiments, as well as the number of experiments actually performed for these objectives are shown in Table 1.
| Efficient Optimizations in Chemistry | |||||
|---|---|---|---|---|---|
| Goal | Method | Number of variables | Number of possible experiments | Number of required experiments | References |
| Synthesis yield | Factorial design | 2–10 | ∼102–104 | ∼10–100 | 6–8,66–89 |
| Protein function | Directed evolution | 2–100 | ∼202–20100 | ∼10–105 | 9–26 |
| Catalytic activity | Genetic algorithm | 4–20 | ∼10–1011 | 60–1000 | 27–39 |
| Material properties | Genetic algorithm | 3–10 | ∼10–1023 | 100–1000 | 40–50 |
The success of chemistry is often attributed to effectively employing practical “rules” governing chemical properties. However, aside from empirical evidence arising from the use of these rules, the underlying reason for why chemistry beats the curse of dimensionality has remained a puzzle. Since this behavior is evident across diverse disciplines in chemistry, as shown in Table 1, the basis for beating the curse of dimensionality must have a generic foundation rooted in some fundamental principles. In order to address this issue, we express optimization of a chemical reaction or property in terms of a fitness function J (e.g., percent synthesis yield), which is dependent on the values of the variables (e.g., concentration of reagent, choice of solvent, etc.). The functional relationship between J and the variables employed defines the fitness landscape.
A synthesis or property optimization may be expressed as an excursion over the fitness landscape, with the goal of finding the absolute best value of J. The topology of the fitness landscape (i.e., number and location of maxima, minima, and saddle points) plays an important role in determining whether optimization will be easy, or even feasible. In many areas of chemistry, fitness landscapes are believed to be rugged (i.e., exhibit many local minima and maxima), for example in the context of optimization of synthesis conditions,51 material properties,33 and protein function.52 The assumption of ruggedness is intuitively reasonable, considering the complex relationship between a synthesis yield or material property and the variables involved.
The concept of a “landscape” in chemistry is commonly associated with free energy landscapes. If minimization of free energy is the goal, for example in the case of protein folding,53 then optimization takes place on the free energy landscape where the variables are the atomic coordinates (e.g., torsional angles).54–56 In the latter case, such landscapes inherently have constraints on the variables because the atoms are of fixed type and bonding arrangement. Constrained free energy landscapes are known to have a rugged topology, with the number of local minima increasing exponentially with the number of atoms.57 In the context of this work, free energy landscapes are a particular class of fitness landscapes. For a general chemical synthesis or property optimization landscape, the constraints can be mild or lifted because the composition may be varied, as well as processing conditions such as temperature and reaction time. This paper considers the topological analysis of these general chemical fitness landscapes. The effects of significant imposed constraints will be considered in this context.
The effect of the topology on the ease of optimization is shown in a graphical illustration of a simple two-dimensional landscape J(x,T) in Fig. 1, where x represents the concentration of a reagent and T is temperature. The landscape in Fig. 1 (a) contains one global maximum and two “traps” at locations M, X1, and X2, respectively. Since searching on this landscape through intuition or other means can easily lead to a suboptimal solution (e.g., beginning from the values of x and T corresponding to point B in Fig. 1 (a), leading to the trap X1), a significant portion of the possible variable values would need to be sampled in order to assure finding the global maximum M. In contrast, a trap-free landscape is often easy to climb, as shown in Fig. 1 (b). The absolute best fitness can be reached when starting from almost any point on the landscape, as indicated by the two paths C and D leading to two equivalent optima at locations M1 and M2, and an exhaustive sampling of all combinations of x and T is unnecessary. Thus, ascertaining the true nature of the topology for the fitness landscape governing chemical optimization is important for determining the ease of finding an optimal solution.
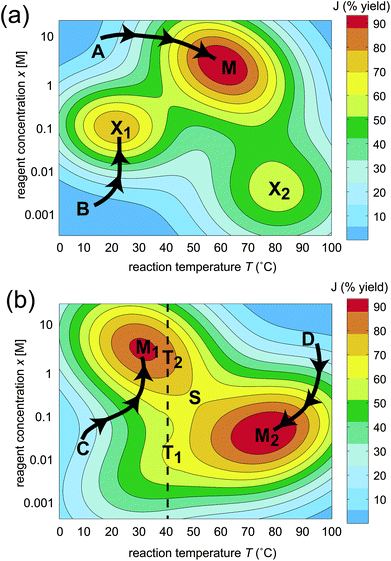 | ||
| Fig. 1 Schematic of two possible generic classes of fitness landscapes illustrated with two variables x (concentration of a reagent) and T (temperature), where J(x,T) represents the percent synthesis yield. The landscape in (a) contains three maxima, one of which is globally optimal (M) and two that are suboptimal (X1 and X2). The landscape in (b) contains two homologous globally optimal maxima M1 and M2 linked by a saddle point S. Constraining the variables, for example fixing the temperature to 40 °C, introduces false traps T1 and T2. | ||
In this work, we show that the inherent topology of fitness landscapes in chemistry explains why the curse of dimensionality can be beaten and identifies practical procedures that can further accelerate chemical optimization. Surprisingly, the topology of fitness landscapes in chemistry may be generically determined, without reference to any specific reaction or property for optimization. This paper will refer to the analysis of fitness landscape topology and its consequences as “OptiChem” theory. In addition to the basic considerations that the maximum synthesis yield is 100% and that physical properties are generally bounded, the conclusions of OptiChem theory rest on two basic assumptions. (i) The optimization goal must be well-posed, meaning that the desired value of J is attainable by some combination of the chosen variables. An example of an ill-posed objective would be a synthesis target containing an atom in an unattainable valence state. (ii) The number and range of the variables must be large enough so as to ensure that free movement over the landscape is permitted, i.e., there are no practical constraints on the variables. For example, imposing the constraint of fixing the temperature at 40 °C while varying the concentration x on the landscape shown in Fig. 1 (b) (the dashed vertical line) would result in encountering two apparent maxima T1 and T2, which are referred to as false traps. Satisfaction of the assumptions (i) and (ii) above provides the basis for the mathematical analysis establishing the fitness landscape topology in chemistry.
The remainder of the work is organized as follows: Section 2 presents the mathematical foundations of OptiChem theory. The latter material draws upon aspects of quantum mechanics and the reader may skip to Section 3, which states the predictions of OptiChem theory and provides an overview of evidence of chemical landscapes in the literature supporting these predictions. Section 4 provides an outlook towards the practical uses of OptiChem theory and offers concluding remarks.
2. Theory
The mathematical foundations of OptiChem theory rely on the general quantum mechanical description of an open system (i.e., a quantum system, such as a molecule, interacting with an environment) and draw from the properties of density matrices58 and convex analysis.59 The reader may choose to skip over this section along with the detailed Supplemental Material† and go directly to Section 3, where the consequences of OptiChem theory may be understood without the mathematical analysis.We seek to determine the topology of the chemical fitness landscape J, which is the mapping of a suitable set of variables p = {p1,p2,…} to the fitness value (e.g., in the illustration of Fig. 1, the temperature is p1 = T and the reagent concentration is p2 = x, with the fitness value being J). The behavior of the fitness landscape J(p) with respect to the variables p is determined by its fundamental quantum-mechanical form60
| J(p) = Tr[ρ(p)O], | (1) |
The state ρ(p) may be determined by the action of a Kraus map (see Electronic Supplemental Material† for details) upon the initial density matrix ρ0,61 for example where ρ0 is the state of the system before the reaction occurs. The Kraus map is written in terms of a matrix Kp, where the superscript denotes the dependence on the variables p. For a system in state ρ0 with m accessible energy levels, the matrix Kp can be expressed as
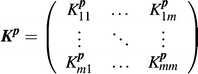 | (2) |
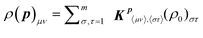 , where 〈μν〉 = μ + m(ν − 1) and analogously for 〈στ〉, and Kp〈μν〉,〈στ〉 is the matrix element of Kp. (see Electronic Supplemental Material† for details). The dependence of Kp upon p could be very complex in many chemical applications; however, the mere existence of the matrix Kp and the ability to fully manipulate it are sufficient to establish the fitness landscape topology.
, where 〈μν〉 = μ + m(ν − 1) and analogously for 〈στ〉, and Kp〈μν〉,〈στ〉 is the matrix element of Kp. (see Electronic Supplemental Material† for details). The dependence of Kp upon p could be very complex in many chemical applications; however, the mere existence of the matrix Kp and the ability to fully manipulate it are sufficient to establish the fitness landscape topology.
Using the above formulation, the fitness J in eqn (1) becomes
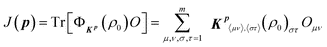 | (3) |
The set of all Kraus matrices generated by sampling the variables p is denoted as {K}. Upon satisfaction of the two assumptions (i) and (ii) in Section 1, it follows that {K} forms a convex set, meaning that for any Kraus matrices K0 and K1, along with any λ ∈ [0,1], their sum Kλ = λK0 + (1 − λ)K1 is also an acceptable Kraus matrix, as shown in the Electronic Supplemental Material†. Since J is a linear function of the Kraus matrices {K}, it also follows that J is a convex function over the set {K}.59 Under these circumstances, convex analysis leads to the conclusion that the resulting fitness landscape contains no local suboptimal maxima to act as traps.62 Thus, there is always a steadily climbing path to the top of the landscape starting from any initial location (i.e., specified by the choice of reagents, processing conditions, etc.), as long as the assumptions (i) and (ii) in Section 1 are satisfied.63,64 A similar analysis (shown in the Supplemental Material†) demonstrates that there are multiple (possibly connected) global optima of J.
3. OptiChem theory predictions and their assessment
In Section 2 and the Electronic Supplemental Material†, we proved the existence of a trap-free topology of the fitness landscape for chemical optimization, subject to the assumptions that the fitness objective is well posed and no practical constraints are imposed on the variables. We also demonstrated that when the above assumptions are satisfied, there exist multiple optimal solutions, i.e., different combinations of the variables can produce the same optimal synthesis yield or property value. These findings lead to three predictions of OptiChem theory:(a) Using more variables should make optimization more effective and efficient: Since a trap-free landscape only exists with sufficient flexibility in the choice of variables, choosing a greater number and range of variables should accelerate the optimization process in terms of reaching the globally optimal fitness value. This conclusion is counterintuitive with respect to common belief and practice in chemistry. The wide success of chemical optimization with as few as two or three variables demonstrates that the number of variables required to form a trap-free landscape may be small in some cases.
(b) Observed suboptimal trapping indicates operation with significantly constrained variables: As a corollary to prediction (a), observation of traps on the landscape implies a violation of assumption (ii), such that some significant limitations are present on the variables, assuming that the objective is well-posed under assumption (i). For example, if the temperature is fixed to 40 °C in Fig. 1 (b), two apparent sub-optimal maxima T1 and T2 may be encountered, both of which are false traps.
(c) Homologous multiple optimal solutions may exist: The allowed presence of multiple global optima on the fitness landscape is consistent with the existence of “homologous” solutions to chemical objectives. For example, for the objective of finding a solvent that produces the fastest alkylation rate of sodium diethyl n-butylmalonate,65 any polar aprotic solvent should produce similar high alkylation rates; these homologous solvents constitute multiple optimal solutions to the objective.
The degree to which the predictions of OptiChem theory hold in the laboratory may be assessed through examination of the extensive literature reporting chemical fitness landscapes. Several issues arise when considering OptiChem theory in practical laboratory optimizations. First, all synthesis or property optimization efforts necessarily constrain the number of variables to a modest set, which could introduce false traps on the landscape because the actual required number of variables can be much larger. Second, various intrinsic features of the variables can limit their dynamic range, e.g. solubility limits may constrain the allowed concentration of a reagent. Finally, the optimal value J* may be unknown a priori for property optimization, and sometimes less than 100% molar yield in a synthesis is the maximum achievable value, thereby making it difficult to determine if traps are present. Despite these caveats, the overwhelming finding is that reported fitness landscapes are almost all trap-free. Although we cannot claim to have performed an exhaustive search of the literature, overall 142 separate fitness landscapes were identified,66–130 with 123 appearing trap-free and with 19 containing traps.131 In some of the latter cases, the traps can be attributed to variable constraints explicitly discussed by the authors; the remaining works make no mention of the presence or absence of traps. Trap-free landscapes have been reported for the chemical synthesis and property goals listed in Table 2. From the list in Table 2, four illustrative studies producing fitness landscapes are summarized in this work; similar landscapes are observed in the references above.
| Trap-free Landscapes in the Chemical Literature | ||
|---|---|---|
| Optimization Goal | References | |
| Synthesis | Organic compounds | 66–74 |
| Polymers | 75–77 | |
| Enzyme-catalyzed* | 78–83 | |
| Biologically catalyzed* | 84–89 | |
| Material catalytic activity | 90–104 | |
| Material Properties | Luminescence | 105–115 |
| Color | 116,117 | |
| X-ray spectral structure | 118,119 | |
| Mechanical constants | 120–123 | |
| Dielectric constants | 124–126 | |
| Electrical resistivity | 127–130 | |
One of the most common objectives in chemistry is to find reaction conditions that produce the highest yield of a desired product. Many studies use methods such as Design of Experiment6,7 to optimize reaction conditions by sampling the available search space and fitting the data points to a polynomial, generating a fitness landscape, while others plot experimental yields directly as a function of the variables. The reported studies almost always produced trap-free landscapes of reaction yield with respect to the variables. Most reported fitness landscapes, obtained by both piecewise linear interpolation and polynomial fitting, contain a single maximum and no saddle points. A typical example of a landscape obtained by direct interpolation of experimental points is shown in Fig. 2 (a), where the lipase-catalyzed production of isopropyl esters of sunflower oil was optimized using enzyme concentration and the molar ratio of oil to alcohol substrates as variables.81 Some fitness landscapes also contain saddle points. For example, the optimization of palladium-catalyzed cyanation of aryl bromides using the ratio of the ligand [(t-Bu)3PH]BF4 to Pd metal and added volume equivalents of water as variables132 revealed a landscape with two disconnected maxima and a saddle point, as shown in Fig. 2 (b).
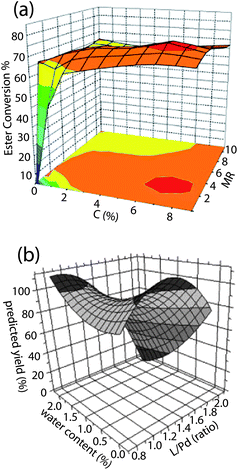 | ||
Fig. 2 (a) Yield of isopropyl ester as a function of catalyst concentration C(%) and substrate molar ratio (MR). The landscape is obtained by linear regression of experimental data points.81 (b) Yield of cyanation product of aryl bromides as a function of ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratio and volume equivalents of water added.132 The landscape is obtained from a polynomial fit of the data points. Pd ratio and volume equivalents of water added.132 The landscape is obtained from a polynomial fit of the data points. | ||
Optimization of solid-state catalytic activity is another common goal. Catalytic activity landscapes are often constructed using the mole fraction of the individual catalyst components as variables. For example, the oxidation of isobutane to methacrolein, isobutene, and CO2 was examined using ternary metal catalysts, where the most effective catalysts contained Mo, V, and Sb as variables.90
Each of the three resulting activity landscapes for the respective products was trap-free, and a large optimal domain of functionally homologous catalysts is present on the landscape for methacrolein, as shown in Fig. 3 (a), consistent with prediction (c) of OptiChem theory. The landscape for isobutene formation with Mo, V, and Sb as variables is shown in Fig. 3 (b) to contain a single optimal point. When Sb was replaced by Bi, the isobutene landscape was found to contain traps (Fig. 3 (c)), but the maximal catalytic activity from the Mo–V–Bi landscape is reduced to 160% of the reference catalyst from over 1200% of the reference for the Mo–V–Sb library. The suboptimal fitness and presence of false traps on the landscape shows that the choice of Bi instead of Sb produces a significant constraint on the variables, in accordance with prediction (b) of OptiChem theory.
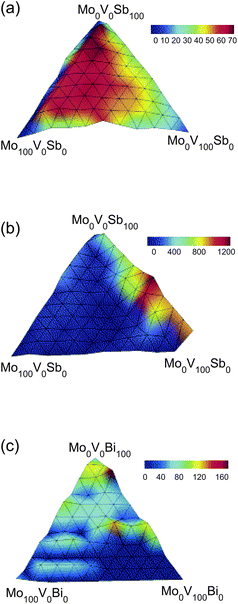 | ||
| Fig. 3 Relative catalytic activity (compared to a fixed literature catalyst) for oxidation of isobutane to form (a) methacrolein with a Mo–V–Sb oxide library, (b) isobutene with a Mo–V–Sb library, and (c) isobutene with a Mo–V–Bi library.90 The landscape for methacrolein formation in (a) contains a large optimal set of functionally homologous solutions with the same activity. The landscape for isobutene formation using Sb is trap free, but that using Bi contains false traps. | ||
Various properties of molecules and materials are also common targets for optimization. For solid-state materials, the variables are often the mole fractions of the components, producing landscapes similar to the catalytic activity landscapes discussed above. Some property optimizations producing trap-free fitness landscapes include luminescence following optical excitation, X-ray spectral structure, mechanical properties, and electrical properties. For optimization of molecular properties, the variables are frequently the functional groups at two or more substitution sites on a molecular scaffold. For example, electrochemical properties were optimized for tetramers with functional group substitution at one site on each monomer unit, for a total of four variables.133 Plotting the variables (i.e., substituents) in order of electron donating ability revealed a fitness landscape that is trap-free to within experimental noise (Fig. 4) and contains a large domain of homologous molecules exhibiting low oxidation potential (red, lower right-hand corner), in accordance with prediction (c).
![The first oxidation potential of oligomers with respect to the electron donating character of substituents.133 The substituents are grouped as R1/R2 (vertical axis) and R3/R4 (horizontal axis) on the same scaffold structure, which resulted in the trap-free landscape shown in the figure. Functionally homologous sets of substituents are found at low oxidation potential (red). The grey squares [a] denote unsynthesized compounds.](/image/article/2011/SC/c0sc00425a/c0sc00425a-f4.gif) | ||
| Fig. 4 The first oxidation potential of oligomers with respect to the electron donating character of substituents.133 The substituents are grouped as R1/R2 (vertical axis) and R3/R4 (horizontal axis) on the same scaffold structure, which resulted in the trap-free landscape shown in the figure. Functionally homologous sets of substituents are found at low oxidation potential (red). The grey squares [a] denote unsynthesized compounds. | ||
4. Discussion
Prior to addressing practical implications of OptiChem theory, it is informative to examine apparent exceptions to the proof of trap-free landscape topology, with a notable example being constrained free energy landscapes, e.g. for protein folding. In the latter case, the fixed nature of the atoms and their bonding arrangement constitutes a severe constraint on the variables. Thus, the documented presence of many traps on these landscapes53,57,134 is not an exception to OptiChem theory, but rather a situation in accordance with prediction (b) of OptiChem theory in Section 3. The efficiency of finding global free energy minima for these landscapes has been attributed to a “funnel” structure containing thermally surmountable small energy barriers separating local traps from the global minimum.54,55,135 Thus, under the right circumstances, general synthesis and property landscapes with mild traps arising from constraints may be successfully traversed, especially with guidance by stochastic algorithms operating in an analogous fashion to thermal fluctuations on free energy landscapes.The surprising observation is that OptiChem theory's prediction of finding trap-free landscapes widely holds for most chemical applications in the presence of seemingly severe constraints. One possible explanation is the opportunity to draw on hundreds of years of collective experience to effectively choose a good set of variables and then proceed to systematically find their optimal values. The evident broad scale success of the latter optimizations, however, can only readily occur because the underlying fitness landscape topology for chemical optimization is so favorable, as set out by OptiChem theory.
OptiChem theory has important practical implications that may improve upon current operations for chemical optimization procedures. The requirement of employing sufficiently flexible variables to take full advantage of the attractive landscape topology leads to the conclusion that optimization should become more effective and efficient as the number and range of the variables increases, contradicting intuitive expectations and the curse of dimensionality. OptiChem theory thus implies, in accordance with prediction (a) above, that the most efficient method for optimizing nominally complex chemical objectives is to simultaneously change all important variables, which is likely best performed with automated high-throughput synthesis and assaying machines guided by advanced pattern-recognition algorithms.136,137 Finally, the success of chemistry is often attributed to the existence of a modest number of “rules” having wide applicability, where traditional discovery of such rules typically follows from lengthy empirical observations. OptiChem theory opens up a systematic means to identify new rules using the metric of landscape topology as a guiding principle. For example, previously unknown structure–property relationships might be deduced based on seeking a small set of variables that produce a trap-free property landscape, as was shown in Ref. 133.
The landscape concepts leading to OptiChem theory were originally developed in the context of laser control of quantum systems.138,139 In the latter case, the goal is to achieve some specified behavior of the target quantum system, such as selective bond breaking,140 maximal fluorescence from a chromophore,141etc.. The variables controlling the quantum system specify the features of a laser field that steers the quantum system to the desired behavior. In contrast to the situation for OptiChem theory, the chemical constituents (e.g., atoms, molecules, or materials) are normally not viewed as variables in laser control. The landscape for laser control with the field structure specifying the variables was demonstrated to have a trap-free topology, and now OptiChem theory shows that the concepts extend to more general optimization in chemistry even without laser fields. Importantly, the diverse domains of laser control and OptiChem share a common landscape topology readily amenable to optimization. Furthermore, chemical optimization and laser control could be combined in order to achieve demanding objectives such as the discovery of materials with specific optical properties.
The chemical sciences are arguably one of the most important endeavors garnering enormous practical benefit. While success can be achieved by employing rules and intuitive simple optimization procedures, left wanting has been a basic explanation for why chemistry is much easier to optimally perform than intuition would suggest. The inherent trap-free chemical landscape topology revealed by OptiChem theory provides the foundation to finally answer this fundamental question.
Acknowledgements
The authors acknowledge support from NSF grant CHE-0718610 and DOE grant DE-FG02-02ER15344. K.W.M. acknowledges the support of an NSF graduate student fellowship. J.D. was supported, in part, by U.S. Department of Energy Contract No. DE-AC02-76-CHO-3073 through the Program in Plasma Science and Technology at Princeton. A.P. acknowledges partial support from RFFI 08-01-00727a, NS-7675.2010.1, and EMALI European Union Marie Curie Teaching-Research Network Contract No. MRTN-CT-2006-035369References
- R. E. Bellman, Dynamic Programming, Princeton University Press, Princeton, NJ., 1957 Search PubMed.
- R. A. Fisher, The Design of Experiments, Oliver and Boyd, London, 1935 Search PubMed.
- C. A. Tracewell and F. H. Arnold, Curr. Opin. Chem. Biol., 2009, 13, 3 CrossRef CAS.
- Methods in Molecular Biology, Vol. 231: Directed Evolution Library Creation: Methods and Protocols, ed. F. H. Arnold and G. Georgiou, Humana, Totowa, 2003 Search PubMed.
- D. E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, Kluwer Academic Publishers, Boston, MA, 1989 Search PubMed.
- G. Hanrahan and K. Lu, Critical Reviews in Analytical Chemistry, 2006, 36, 151.
- O. W. Gooding, Curr. Opin. Chem. Biol., 2004, 8, 297 CrossRef CAS.
- M. A. Bezerra, R. E. Santelli, E. P. Oliveira, L. S. Villar and L. A. Escaleira, Talanta, 2008, 76, 965 CrossRef CAS.
- C. H. Collins, F. H. Arnold and J. R. Leadbetter, Mol. Microbiol., 2005, 55, 712 CrossRef CAS.
- T. S. Wong, F. H. Arnold and U. Schwaneberg, Biotechnol. Bioeng., 2004, 85, 351 CrossRef.
- T. Bulter, M. Alcade, V. Sieber, P. Meinhold, C. Schlachtbauer and F. H. Arnold, Appl. Environ. Microbiol., 2003, 69, 987 CrossRef CAS.
- M. T. Reetz, D. Kahakeaw and J. Sanchis, Mol. BioSyst., 2009, 5, 115 RSC.
- M. T. Reetz and S. Wu, Chem. Commun., 2008, 5499 RSC.
- M. T. Reetz, D. Kahakeaw and R. Lohmer, ChemBioChem, 2008, 9, 1797 CrossRef CAS.
- M. T. Reetz and J. D. Carballeira, Nat. Protoc., 2007, 2, 891 Search PubMed.
- M. T. Reetz, M. Puls, J. D. Carballeira, A. Vogel, K.-E. Jaeger, T. Eggert, W. Thiel, M. Bocola and N. Otte, ChemBioChem, 2007, 8, 106 CrossRef CAS.
- M. T. Reetz, M. Bocola, J. D. Carballeira and A. Vogel, Angew. Chem. Int. Ed., 2006, 45 Search PubMed.
- M. T. Reetz, J. D. Carballeira, D. Zha and A. Vogel, Angew. Chem. Int. Ed., 2005, 44 Search PubMed.
- M. T. Reetz, C. Torre, A. Eipper, R. Lohmer, M. Hermes, B. Brunner, A. Maichele, M. Bocola, M. Arand, A. Cronin, Y. Genzel, A. Archelas and R. Furstoss, Org. Lett., 2004, 6 Search PubMed.
- D. Zha, S. Wilensek, M. Hermes, K.-E. Jaeger and R.M.T., Chem. Commun., 2001, 2664 RSC.
- M. T. Reetz, Pure Appl. Chem., 2000, 72, 1615 CrossRef CAS.
- D. Umeno, A. V. Tobias and F. H. Arnold, J. Bacteriol., 2002, 184, 6690 CrossRef CAS.
- S. Ahmad, M. Z. Kamal, S.R. and N. M. Rao, J. Mol. Biol., 2008, 381, 324 CrossRef CAS.
- E. G. Hibbert, T. Senussi, M. E. B. Smith, S. J. Costelloe, J. M. Ward, H. C. Hailes and P. A. Dalby, J. Biotechnol., 2008, 134, 240 CrossRef CAS.
- E. G. Hibbert, T. Senussi, S. J. Costelloe, W. Lei, M. E. B. Smith, J. M. Ward, H. C. Hailes and P. A. Dalby, J. Biotechnol., 2007, 131, 425 CrossRef CAS.
- K. Miyazaki, M. Takenouchi, H. Kondo, N. Noro, M. Suzuki and S. Tsuda, J. Biol. Chem., 2006, 281, 10236 CrossRef CAS.
- U. Rodemerck, D. Wolf, O. V. Buyevskaya, P. Claus, S. Senkan and M. Baerns, Chem. Eng. J., 2001, 82, 3 CrossRef CAS.
- O. V. Buyevskaya, A. Brueckner, E. V. Kondratenko, D. Wolf and M. Baerns, Catal. Today, 2001, 67, 369 CrossRef.
- D. Wolf, O. V. Buyevskaya and M. Baerns, Appl. Catal., A, 2000, 200, 63 CrossRef CAS.
- O. V. Buyevskaya, D. Wolf and M. Baerns, Catal. Today, 2000, 62, 91 CrossRef CAS.
- S. Moehmel, N. Steinfeldt, S. Engelschalt, M. Holena, S. Kolf, M. Baerns, U. Dingerdissen, D. Wolf, R. Weber and M. Bewersdorf, Appl. Catal., A, 2008, 334, 73 CrossRef CAS.
- M. F.-D. Clerc, F. Lengliz, C. Mirodatos, S. R. M. Pereira and R. Rakotomalala, Rev. Sci. Instrum., 2005, 76, 062208 CrossRef.
- T. Umegaki, Y. Watanabe, N. Nukui, K. Omata and M. Yamada, Energy Fuels, 2003, 17, 850 CrossRef CAS.
- K. Omata, T. Ozkai, T. Umegaki, Y. Watanabe, N. Nukui and M. Yamada, Energy Fuels, 2003, 17, 836 CrossRef CAS.
- Y. Watanabe, T. Umegaki, M. Hashimoto, K. Omata and M. Yamada, Catal. Today, 2004, 89, 455 CrossRef CAS.
- J. M. Serra, A. Chica and A. Corma, Appl. Catal., A, 2003, 239, 35 CrossRef CAS.
- Y. Yamada, A. Ueda, K. Nakagawa and T. Kobayashi, Res. Chem. Intermed., 2002, 28, 397 CrossRef CAS.
- J. Paul, R. Jannsens, J. F. M. Denayer, G. V. Baron and P. A. Jacobs, J. Comb. Chem., 2005, 7, 407 CrossRef CAS.
- A. Corma, J. M. Serra, P. Serna, S. Valero, E. Argente and V. Botti, J. Catal., 2005, 229, 513 CrossRef CAS.
- U. Rodemerck, M. Baerns, M. Holena and D. Wolf, Appl. Surf. Sci., 2004, 223, 168 CrossRef CAS.
- J. Singh, M. A. Ator, E. P. Jaeger, M. P. Allen, D. A. Whipple, J. E. Soloweij, S. Chowdhary and A. M. Treasurywala, J. Am. Chem. Soc., 1996, 118, 1669 CrossRef CAS.
- L. Wever, S. Wallbaum, C. Broger and K. Gubernator, Angew. Chem., Int. Ed. Engl., 1995, 34, 2280 CrossRef CAS.
- M. Bulut, L. E. M. Gevers, J. Paul, I. F. J. Vankelecom and P. A. Jacobs, J. Comb. Chem., 2006, 8, 168 CrossRef CAS.
- A. Rusinko, S. S. Young, D. H. Drewry and S. W. Gerritz, Comb. Chem. High T. Scr., 2002, 5, 125 Search PubMed.
- C. Kulshreshtha, A. K. Sharma and K.-S. Sohn, J. Comb. Chem., 2008, 10, 421 CrossRef CAS.
- K.-S. Sohn, D. H. Park, S. H. Cho, B. I. Kim and S. I. Woo, J. Comb. Chem., 2006, 8, 44 CrossRef CAS.
- Y. S. Jung, C. Kulshreshtha, J. S. Kim, N. Shin and K. S. Sohn, Chem. Mater., 2007, 19, 5309 CrossRef CAS.
- K.-S. Sohn, D. H. Park, S. H. Cho, J. S. Kwak and J. S. Kim, Chem. Mater., 2006, 18, 1768 CrossRef CAS.
- K.-S. Sohn, B. I. Kim and N. Shin, J. Electrochem. Soc., 2004, 151, H243 CrossRef CAS.
- K.-S. Sohn, J. M. Lee and N. Shin, Adv. Mater., 2003, 15, 2081 CrossRef CAS.
- G. E. P. Box and K. B. Wilson, J. Roy. Stat. Soc. B Met., 1951, 13, 1 Search PubMed.
- R. J. Fox and G. W. Huisman, Trends Biotechnol., 2008, 26, 132 CrossRef CAS.
- J. Onuchic, Z. LutheySchulten and P. Wolynes, Annu. Rev. Phys. Chem., 1997, 48, 545 CrossRef CAS.
- D. J. Wales, Philos. Trans. R. Soc. London, Ser. A, 2005, 363, 357 CrossRef CAS.
- D. J. Wales, Int. Rev. Phys. Chem., 2006, 25, 237 CrossRef CAS.
- D. J. Wales, Curr. Opin. Struct. Biol., 2010, 20, 3 CrossRef CAS.
- F. Stillinger and T. Weber, Science, 1984, 225, 983 CAS.
- E. B. Davies, Quantum Theory of Open Systems, Academic Press, London, New York, 1976 Search PubMed.
- S. P. Boyd and L. Vandenberghe, Convex Optimization, Cambridge, UK; New York, 2004 Search PubMed.
- F. Schwabl, Quantum Mechanics, Springer Verlag, Berlin, 2002 Search PubMed.
- K. Kraus, States, Effects and Operations: Fundamental Notions of Quantum Theory, Springer-Verlag, Berlin, 1983 Search PubMed.
- R. T. Rockafellar, Convex analysis, Princeton University Press, Princeton, 1970 Search PubMed.
- R. Wu, A. Pechen, H. Rabitz, M. Hsieh and B. Tsou, J. Math. Phys., 2008, 49, 022108 CrossRef.
- (a) A. Pechen, D. Prokhorenko, R. Wu and H. Rabitz, J. Phys. A: Math. Theor., 2008, 41, 045205 CrossRef; (b) A. Pechen and H. R. Rabitz, Europhysics Letters, 2010, 91, 60005 CrossRef.
- H. E. Zaugg, J. Am. Chem. Soc., 1961, 83, 837 CrossRef CAS.
- J. C. Conrad, J. Kong, B. N. Laforteza and D. W. C. MacMillan, J. Am. Chem. Soc., 2009, 131, 11640 CrossRef CAS.
- P. J. Hogan, P. A. Hopes, W. O. Moss, G. E. Robinson and I. Patel, Org. Proc. Res. Dev Search PubMed.
- N. Sanchez, M. Martinez and J. Aracil, Ind. Eng. Chem. Res., 1997, 36, 1529 CrossRef CAS.
- V. K. Aggarwal, A. C. Staubitz and M. Owen, Org. Process Res. Dev., 2006, 10, 64 Search PubMed.
- T. N. Glasnov, H. Tye and C. O. Kappe, Tetrahedron, 2008, 64, 2035 CrossRef CAS.
- C. Y. Thien, A. R. Mohamed and S. Bhatia, J. Chem. Technol. Biotechnol., 2007, 82, 81 CrossRef CAS.
- F. Stazi, G. Palmisano, M. Turconi and M. Santagostino, J. Org. Chem., 2004, 69, 1097 CrossRef CAS.
- C.-J. Shieh and Y.-F. Lai, J. Agric. Food Chem., 2000, 48, 1124 CrossRef CAS.
- L. F. Bautista, M. Martinez and J. Aracil, Chem. Eng. Technol., 1997, 20, 287 CrossRef CAS.
- D. B. McKie and S. Lepeniotis, Chemom. Intell. Lab. Syst., 1998, 41, 105 CrossRef CAS.
- K. T. Hwang, S. T. Jung, G. D. Lee, M. S. Chinnan, Y. S. Park and H. J. Park, J. Agric. Food Chem., 2002, 50, 1876 CrossRef CAS.
- A. Kukovecz, D. Mehn, E. Nemes-Nagy, R. Szabo and I. Kiricsi, Carbon, 2005, 43, 2842–2849 CrossRef CAS.
- D.-H. Zhang, S. Bai, X.-Y. Dong and Y. Sun, J. Agric. Food Chem., 2007, 55, 4526 CrossRef CAS.
- Y. Yasin, M. Basri, F. Ahmad and A. B. Salleh, J. Chem. Technol. Biotechnol., 2008, 83, 694 CrossRef CAS.
- L.-X. Lv, Y.-Q. Chen and S.-Y. Li, J. Sci. Food Agric., 2007, 88, 659.
- A. Bouaid, J. Aparicio, M. Martinez and J. Aracil, Enzyme Microb. Technol., 2007, 41, 533 CrossRef CAS.
- E. Soo, A. Salleh, M. Basri, R. Rahman and K. Kamaruddin, Process Biochem., 2004, 39, 1511–1518 CrossRef CAS.
- M. Basri, R. Rahman, A. Ebrahimpour, A. Salleh, E. Gunawan and M. Rahman, BMC Biotechnol., 2007, 7, 53 CrossRef.
- J. H. Sim, A. H. Kamaruddin and W. S. Long, Biochem. Eng. J., 2008, 40, 337 CrossRef CAS.
- G. Prakash and A. K. Siristava, Biochem. Eng. J., 2008, 40, 218 CrossRef CAS.
- J. H. Sim, A. H. Kamaruddin, W. S. Long and G. Najafpour, Enzyme Microb. Technol., 2007, 40, 1234–1243 CrossRef CAS.
- Z. Tokcaer, E. Bayraktar, U. Mehmetoglu, G. Ozcengiz and N. G. Alaeddinoglu, Process Biochem., 2006, 41, 350–355 CrossRef CAS.
- H. Valera, J. Gomes, S. Lakshmi, R. Gururaja, S. Suryanarayan and D. Kumar, Enzyme Microb. Technol., 2005, 37, 521–526 CrossRef CAS.
- A. Ebrahimpour, R. Rahman, D. Ean Ch'ng, M. Basri and A. Salleh, BMC Biotechnol., 2008, 8, 96 CrossRef.
- J. S. Paul, P. A. Jacobs, P. W. Weiss and W. F. Maier, Appl. Catal., A, 2004, 265, 185 CrossRef CAS.
- P. J. Cong, R. D. Doolen, Q. Fan, D. M. Giaquinta, S. H. Guan, E. W. McFarland, D. M. Poojary, K. Self, H. W. Turner and W. H. Weinberg, Angew. Chem., Int. Ed., 1999, 38, 483 CrossRef.
- J. W. Saalfrank and W. F. Maier, C.R. Chemie, 2004, 7, 483 Search PubMed.
- A. Richter, M. Langpape, S. Kolf, G. Grubert, R. Eckelt, J. Radnik, A. Schneider, M. M. Pohl and R. Fricke, Appl. Catal., B, 2002, 36, 261 CrossRef CAS.
- Z. M. Liu, K. S. Oh and S. I. Woo, Catal. Surv. Asia, 2006, 10, 8 CrossRef CAS.
- Y. Liu, P. Cong, R. D. Doolen, S. Guan, V. Markov, L. Woo, S. Zeyss and U. Dingerdissen, Appl. Catal., A, 2003, 254, 59 CrossRef CAS.
- P. J. Cong, A. Dehestani, R. Doolen, D. M. Giaquinta, S. H. Guan, V. Markov, D. Poojary, K. Self, H. Turner and W. H. Weinberg, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11077 CrossRef CAS.
- S. Senkan, S. Ozturk, K. Krantz and I. Onal, Appl. Catal., A, 2003, 254, 97 CrossRef CAS.
- K. Krantz, S. Ozturk and S. Senkan, Catal. Today, 2000, 62, 281 CrossRef CAS.
- M. Seyler, K. Stoewe and W. F. Maier, Appl. Catal., B, 2007, 76, 146 CrossRef CAS.
- S. Senkan, K. Krantz, S. Ozturk, V. Zengin and I. Onal, Angew. Chem., Int. Ed., 1999, 38, 2794 CrossRef CAS.
- Q. X. Dai, H. Y. Xiao, W. S. Li, Y. Q. Na and X. P. Zhou, Appl. Catal., A, 2005, 290, 25 CrossRef CAS.
- J. H. Park, P. Shakkthivel, H. J. Kim, M. K. Han, J. H. Jang, Y. R. Kim, H. S. Kim and Y. G. Shul, Int. J. Hydrogen Energy, 2008, 33, 1845 CrossRef CAS.
- J. S. Cooper and P. J. McGinn, Appl. Surf. Sci., 2007, 254, 662 CrossRef CAS.
- J. S. Cooper and P. J. McGinn, J. Power Sources, 2006, 163, 330 CrossRef CAS.
- K. S. Sohn, I. W. Zeon, H. Chang, K. L. Seung and H. D. Park, Chem. Mater., 2002, 14, 2140 CrossRef CAS.
- K. S. Sohn, J. G. Yoo, N. Shin, K. Toda and D. S. Zang, J. Electrochem. Soc., 2005, 152, H213 CrossRef CAS.
- S. Y. Seo, K. S. Sohn, H. D. Park and S. Lee, J. Electrochem. Soc., 2002, 149, H12 CrossRef CAS.
- D. H. Park, S. H. Cho, J. S. Kim and K. S. Sohn, J. Alloys Compd., 2008, 449, 196 CrossRef CAS.
- J. K. Park, K. J. Choi, H. G. Kang, J. M. Kim and C. H. Kim, Electrochem. Solid-State Lett., 2007, 10, J15 CrossRef CAS.
- J. K. Park, J. M. Kim, K. N. Kim, C. H. Kim and H. D. Park, Electrochem. Solid-State Lett., 2004, 7, H39 CrossRef CAS.
- K. S. Sohn, C. H. Kim, J. T. Park and H. D. Park, J. Mater. Res., 2002, 17, 3201 CrossRef CAS.
- C. H. Kim, S. M. Park, J. K. Park, H. D. Park, K. S. Sohn and J. T. Park, J. Electrochem. Soc., 2002, 149, H183 CrossRef.
- J. K. Park, K. J. Choi, K. N. Kim and C. H. Kim, Appl. Phys. Lett., 2005, 87, 031108 CrossRef.
- K. S. Sohn, S. Y. Seo and H. D. Park, Electrochem. Solid-State Lett., 2001, 4, H26 CrossRef CAS.
- R. Takahashi, H. Kubota, M. Murakami, Y. Yamamoto, Y. Matsumoto and H. Koinuma, J. Comb. Chem., 2004, 6, 50 CrossRef CAS.
- T. S. Chan, C. C. Kang, R. S. Liu, L. Chen, X.-N. Liu, J.-J. Ding, J. Bao and C. Gao, J. Comb. Chem., 2007, 9, 343 CrossRef CAS.
- T. Konishi, T. Hondo, T. Araki, N. Keishi, T. Tsuchiya, T. Matsumoto, S. Suehara, S. Todoroki and S. Inoue, J. Non-Cryst. Solids, 2003, 324, 58 CrossRef CAS.
- R. Zarnetta, A. Savan, S. Thienhaus and A. Ludwig, Appl. Surf. Sci., 2007, 254, 743 CrossRef CAS.
- R. Takahashi, Y. Yonezawa, M. Ohtani, M. Kawasaki, Y. Matsumoto and H. Koinuma, Appl. Surf. Sci., 2006, 252, 2477 CrossRef CAS.
- Y. Yokoyama, J. Non-Cryst. Solids, 2003, 316, 104 CrossRef CAS.
- D. Tanda, T. Tanabe, R. Tamura and S. Takeuchi, Mater. Sci. Eng., A, 2004, 387–389, 991 CrossRef.
- J.-C. Zhao, M. R. Jackson, L. A. Peluso and L. N. Brewer, JOM, 2002, 54, 42 CrossRef CAS.
- B. Xia, F. Chen, S. A. Campbell, J. T. Roberts and W. L. Gladfelter, Chem. Vap. Deposition, 2004, 10, 195 CrossRef CAS.
- K. Hasegawa, P. Ahmet, N. Okazaki, T. Hasegawa, K. Fujimoto, M. Watanabe, C.T. and H. Koinuma, Appl. Surf. Sci., 2004, 223, 229 CrossRef CAS.
- R. B. van Dover and L. F. Schneemeyer, Macromol. Rapid Commun., 2004, 25, 150 CrossRef.
- L. F. Schneemeyer, R. B. van Dover and R. M. Fleming, Appl. Phys. Lett., 1999, 75, 1967 CrossRef CAS.
- R. Yamauchi, S. Hata, J. Sakurai and A. Shimokohbe, Jpn. J. Appl. Phys., 2006, 45, 5911 CrossRef CAS.
- R. Loebel, S. Thienhaus, A. Savan and A. Ludwig, Mater. Sci. Eng., A, 2008, 481–482, 151 CrossRef.
- F. Tsui and Y. S. Chu, Macromol. Rapid Commun., 2004, 25, 189 CrossRef CAS.
- D. A. Kukuruznyak, P. Ahmet, T. Chikyow, A. Yamamoto and F. S. Ohuchi, J. Appl. Phys., 2005, 98, 043710 CrossRef.
- We include as “traps” only those cases where a clear sub-optimal maximum is present, as in the schematic illustration Fig. 1(a).
- F. Stazi, G. Palmisano, M. Turconi and M. Santagostino, Tetrahedron Lett., 2005, 46, 1815 CrossRef CAS.
- C. A. Briehn, M. S. Schiedel, E. M. Bonsen, W. Schuhmann and P. Baeuerle, Angew. Chem., Int. Ed., 2001, 40, 4680 CrossRef CAS.
- J. Bryngelson and P. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7524.
- D. J. Wales and T. V. Bogdan, J. Phys. Chem. B, 2006, 110, 20765 CrossRef CAS.
- C. Jaekel and R. Paciello, Chem. Rev., 2006, 106, 2912 CrossRef.
- R. D. King, J. Rowland, S. G. Oliver, M. Young, W. Aubrey, E. Byrne, M. Liakata, M. Markham, L. N. Pir, P. Soldatova, A. Sparkes, K. E. Whelan and A. Clare, Science, 2009, 324, 85 CrossRef CAS.
- H. Rabitz, M. Hsieh and C. Rosenthal, Science, 2004, 303, 1998–2001 CrossRef CAS.
- T. Ho and H. Rabitz, J. Photochem. Photobiol., A, 2006, 180, 226 CrossRef CAS.
- R. Levis, G. Menkir and H. Rabitz, Science, 2001, 292, 709 CrossRef CAS.
- J. L. Herek, W. Wohlleben, R. J. Cogdell, D. Zeidler and M. Motzkus, Nature, 2002, 417, 533 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Proof of fitness landscape topology. See DOI: 10.1039/c0sc00425a |
| This journal is © The Royal Society of Chemistry 2011 |
