Tailoring Au-core Pd-shell Pt-cluster nanoparticles for enhanced electrocatalytic activity

Abstract

We have rationally synthesized and optimized catalytic nanoparticles consisting of a gold core, covered by a palladium shell, onto which platinum clusters are deposited (Au@Pd@Pt NPs). The amount of Pt and Pd used is extremely small, yet they show unusually high activity for electrooxidation of formic acid. The optimized structure has only 2 atomic layers of Pd and a half-monolayer equivalent of Pt (θ_Pt ≈ 0.5) but a further increase in the loading of Pd or Pt will actually reduce catalytic activity, inferring that a synergistic effect exists between the three different nanostructure components (sphere, shell and islands). A combined electrochemical, surface-enhanced Raman scattering (SERS) and density functional theory (DFT) study of formic acid and CO oxidation reveals that our core–shell–cluster trimetallic nanostructure has some unique electronic and morphological properties, and that it could be the first in a new family of nanocatalysts possessing unusually high chemical reactivity. Our results are immediately applicable to the design of catalysts for direct formic acid fuel cells (DFAFCs).

---

Introduction

Cheap catalysts amenable for use in low-resource settings (e.g., fuel cell catalysts with a reduced Pt loading) are ever in high demand.^1–5 In order to reduce cost (by reducing the amount of Pt in the catalyst) and simultaneously increase efficiency, Pt-based bimetallic and trimetallic nanoparticle (NP) catalysts have been developed.^6–9 These NPs exhibit different properties and functionalities when compared to monometallic Pt. In particular, they show enhanced selectivity and reactivity when used as catalysts and sensors.^10–14 Trimetallic NPs may possess an even greater degree of catalytic activity and selectivity than the bimetallic ones because more variables are available for tuning; however, there have been only a few reports of trimetallic NPs in the literature thus far.^15–17 In accordance with the increased degrees of freedom that trimetallic NPs offer, the optimization of composition and morphology presented in this work has been a great challenge.

Our group has recently developed a seed-mediated growth method to synthesize several kinds of core–shell NPs, and we have investigated the mechanism of different growth modes for bimetallic core–shell NPs.^18,19 We have proposed that the atomic radius, cohesive energy, and electronegativity of the core and shell metals could be three key factors in determining whether the shell growth mode is an epitaxial or island one. For example, Pd can grow layer-by-layer on Au,^20,21 while Pt in general prefers the island mode on Au and Pd surfaces.¹⁸ It is of interest to take advantage of two different growth modes and thus synthesize trimetallic core–shell–cluster NPs with improved chemical and physical properties for catalysis.

Formic acid (HCOOH) is nontoxic, and direct formic acid fuel cells (DFAFCs) are able to achieve a higher power density than direct methanol fuel cells (DMFCs) although the energy density of methanol is higher than that of formic acid.²²Formic acid exhibits a smaller crossover flux through Nafion than methanol,²³ allowing the use of highly concentrated fuel solutions and thinner membranes.¹ The high energy density, fast oxidation kinetics, and convenience of liquid formic acid, as well as the simplicity of power-system integration, make DFAFCs a promising power source for portable device applications.^24,25 Considerable progress in different aspects of DFAFC research and engineering has been achieved in recent years, and it has enabled DFAFC technology to be implemented in practical devices.¹

In this work we report the synthesis and optimization of catalytic NPs consisting of a Au core, covered by a Pd shell, onto which Pt clusters are deposited (hereafter denoted as Au@Pd@Pt NPs). The amount of Pt and Pd used is extremely small, yet they show unusually high activity for electrochemical oxidation of formic acid. This activity is critically dependent upon the Pd-shell thickness and the Pt-cluster coverage. A complex synergistic effect is achieved by using all three metals in combination (i.e., the whole is greater than the sum of its parts). In order to understand this synergistic effect, we used in situsurface-enhanced Raman scattering (SERS) to characterize species present on the surface during the chemical reaction and density functional theory (DFT) calculations to reveal why small changes in the NP structure can dramatically change their catalytic activity.

Experimental

Electrochemical and spectroelectrochemical studies

Electrochemical measurements were conducted using a CHI 631B electrochemical workstation (CH Instruments, China).

Raman spectra were recorded on a LabRam I confocal microprobe Raman system (Jobin-Yvon, France). The excitation wavelength was 632.8 nm from a He–Ne laser, with a power of about 4 mW on the sample.

A spectroelectrochemical cell with a Pt wire and a saturated calomel electrode (SCE) serving as the counter and the reference electrodes respectively were used for both the electrochemical and the in situ spectroelectrochemical SERS measurements.²⁶ All potentials given in this work are relative to an SCE. Glassy carbon (GC), covered with NPs, acted as the working electrode. The active surface area of the working electrode was determined by hydrogen adsorption/desorption and confirmed by oxygen adsorption/desorption as in the literature,^10,27–29 except measurements made for the 16 and 9 nm NPs on carbon black were normalized by mass.

The extent of hydrogen or oxygen adsorption will vary from one NP material to another, and this will lead to error in the calculation of working electrode surface area. Several methods have been devised for estimating surface area, including under potential deposition (UPD), hydrogen adsorption/desorption, oxygen adsorption/desorption (or oxide formation/reduction), and the oxidation of a probe molecule that has a characteristic surface coverage such as CO. However, a standard method of estimating surface area for bimetallic NPs does not currently exist. We used a combination of methods (hydrogen adsorption/desorption at our Pd–Pt bimetallic NP surfaces, as in the literature of the Yang,¹⁰ Feliu³⁰ and Adzic³¹groups, followed by confirmation with oxygen adsorption/desorption) and found that the surface areas obtained agree within 20%.

A GC disk electrode with diameter = 3 mm was used as the support. It was prepared for use by mechanical polishing with successively finer grades of alumina powder to achieve a mirror-finish surface: 3 to 0.05 μm (Buehler Ltd., USA). It was cleaned by sonication in Millipore water for 3 min after each polishing step; then after polishing, it was cleaned electrochemically in 0.5 M H₂SO₄ by scanning the potential between −0.25 and 1.25 V at 500 mV s⁻¹ for 10 min.

Imaging

Scanning Electron Microscope (SEM) images were acquired using a LEO1530 (Leo, Germany). Transmission Electron Microscope (TEM) and high-resolution TEM (HRTEM) images were acquired using a Tecnai F30 (FEI, The Netherlands) and a JEOL 4000EX (JEOL, Japan).

DFT calculations

All calculations were performed using the DFT total-energy Vienna ab initio simulation package (VASP).¹² The projector augmented-wave method (PAW) and the Perdew–Burke–Ernzerhof generalized-gradient approximation (GGA-PBE) were employed for the exchange–correlation functional, and the wave functions were expanded in a plane-wave basis set with an energy cutoff of 400 eV. The theoretically optimized lattice constants were 4.174 and 3.953 Å for Au and Pd, respectively. These results are in good agreement with experimental values, which are 4.078 Å for Au and 3.891 Å for Pd.³² Au@Pd@Pt NPs with 2 atomic layers of Pd were simulated using 2 p3 × 3 Au(111) layers, 2 p3 × 3 Pd(111) layers, and a Pt₄ cluster. The Au lattice constant was used for Pd. Au@Pd@Pt NPs with ≥5 atomic layers of Pd were simulated using 4 Pd layers with the Pd lattice constant and a Pt₄ cluster. CO was initially placed on a Pd bridge site and a Pt top site. The induced dipole moment was taken into account by applying a dipole correction.^33,34 We allowed atomic relaxation of the CO molecule and of all metal atoms except for the bottom layer of the slab in all directions. The final forces on the atoms were less than 0.02 eV Å⁻¹. For the k-point sampling, a 4 × 4 × 1 mesh of gamma-centered grids generated 6 k points in the irreducible Brillouin zone (IBZ) for the Brillouin zone integration. The Methfessel and Paxton method³⁵ was used with a temperature broadening of k_BT = 0.01 eV to improve convergence (k_B = the Boltzmann constant, T = temperature) and the total energy was extrapolated to 0 K. The PAW potential was generated taking scalar relativistic corrections into account.

Results and discussion

Synthesis of the Au@Pd@Pt NPs

The seed-mediated growth method of preparing Au@Pd@Pt NPs is shown schematically in Fig. 1. The virtue of this method for preparing core–shell–cluster NPs is that the shell thickness and cluster coverage can be routinely controlled by simply adjusting the molar ratios of the second and third metal ions to Au seeds in solution.¹⁹ The moles of Pd required in solution were determined by taking into consideration the total surface area of the Au-core particles to be covered, and the number of Pd atoms which are necessary to cover them with the desired number of monolayers (in this work we use “monolayers” to mean “atomic layers”).¹⁹ An extra 25% was added to ensure complete formation of each monolayer.³⁶ The moles of Pt required in solution were determined by taking into consideration the desired Pt to Pd and Pt to Au geometrical-volume ratios and the Pt to Pd and Pt to Au molar-volume ratios. It is important to note that Pt grows on Pd as a set of clusters and not as a set of consecutive monolayers; however, we will use monolayer-equivalents (hereafter denoted θ_Pt) as a convenient method for describing the amount of Pt added to each NP.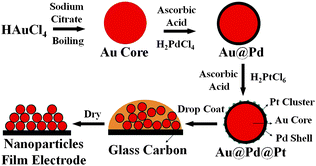

Fig. 1 The procedure used to prepare a Au@Pd@Pt NP film on a GC electrode.

We now describe the synthesis of NPs with a 55 nm Au core, covered by 2 monolayers of Pd, and having Pt clusters added such that the amount of Pt is approximately equivalent to the amount that would be present in half a monolayer (θ_Pt ≈ 0.5). A sol containing Au seeds, with a diameter of about 55 nm, was synthesized according to Frens' method.³⁷ In order to add 2 monolayers of Pd onto the surface of the Au, 30 mL of the sol were mixed with 0.8 mL of 1 mM aqueous H₂PdCl₄ (PdCl₂, 99.9%, Alfa Aesar) and then cooled to 0 °C in an ice bath. Next, 0.4 mL of 10 mM aqueous ascorbic acid (99%, Shanghai Reagent Co. of Chinese Medicine) was added to the mixture through a syringe controlled by a step motor while stirring. The mixture was then stirred for 30 min to ensure a complete reduction of H₂PdCl₄. The color of the mixture turned from red–brown to dark brown, indicating the formation of products.^19,38 In order to add Pt clusters with θ_Pt ≈ 0.5 onto the surface of the Pd, the above solution was heated to 80 °C and 171 μL of 1 mM aqueous H₂PtCl₆ (99%, Shanghai Reagent Co. of Chinese Medicine) were dropped in. Then 86 μL of 10 mM ascorbic acid were added to the mixture, and it was allowed to react for another 30 min to ensure complete reduction of H₂PtCl₆. Finally, 1 mL of the Au@Pd@Pt NP solution was centrifuged for 15 min, washed with Millipore water, added to the 3 mm GC disk electrode, and then dried.³⁶ The loading of Pt and Pd on NPs prepared in this way was found to be about 28.7 μg cm⁻² (this number is a sum for both metals). The Au : Pd : Pt molar ratio is about 100 : 6 : 1.

Our previous electrochemical and Raman characterizations have shown that the Pd shell of the Au@Pd NPs can grow in an epitaxial mode to yield a pinhole-free coating, even at a thickness of only two atomic layers.^18,36 However, the Pt clusters grow by an island mode because of their high cohesive energy. We present evidence for a distinct core–shell–cluster structure over an alloy structure in electronic supporting information (ESI) section S1.† In the present study, the coverage of Pt on Pd is very low, typically less than one monolayer-equivalent (θ_Pt < 1). It may therefore be reasonable to assume the model that each Pt cluster is formed as a pyramid of four atoms by the island growth mode.

These NPs were characterized by SEM, TEM and HRTEM (Fig. 2). They have a uniform size distribution and exhibit a spherical shape. As can be seen in Fig. 2A–C, it is extremely difficult to distinguish a very small Pt cluster formed by several atoms (when θ_Pt ≈ 0.5) from the Pd substrate. This is because there is only a small lattice mismatch of 0.77% between Pt and Pd metals.³⁹ When we increased the size of the Pt clusters (θ_Pt ≈ 2.0), however, it became easier to see their surface structure (Fig. 2D–F). When the coverage of Pt was further increased to θ_Pt > 15, the island structure became clearly visible (Fig. 2G–I). We also used SERS to characterize the surface of our NPs. Additional images are presented in section S1 (Au core) and section S2 (Ag core) of the ESI.†

Fig. 2 Typical SEM (A), TEM (B) and HRTEM (C) images of 55 nm Au@Pd@Pt NPs with 2 monolayers of Pd and θ_Pt ≈ 0.5. Typical TEM (D and E) and HRTEM (F) images of 16 nm Au@Pd@Pt NPs with 2 monolayers of Pd and θ_Pt ≈ 2.0. Typical SEM (G), TEM (H) and HRTEM (I) images of 55 nm Au@Pd@Pt NPs with 2 monolayers of Pd and θ_Pt ≈ 20.0.

Characterization of the Au@Pd@Pt NP surface by SERS

Apart from HRTEM, an alternative way to detect the very small Pt clusters formed when θ_Pt ≈ 0.5 is to employ a probe molecule and SERS strategy. CO is a widely used probe whose vibrational frequency is quite sensitive to changes in the way it binds to metals and its local environment when adsorbed. We therefore used SERS and analyzed the coverage-dependent frequency changes observed for CO when adsorbed on our Au@Pd@Pt NPs in a CO-saturated electrolyte solution.

According to the literature, CO will occupy three-fold-hollow sites on a pure Pd surface at low coverage.^40,41 Then as the coverage of CO is increased, it will tend to bridge two Pd atoms instead;⁴² this may be seen in Fig. 3 (bridge-site adsorption, Raman shift ≈ 1950 cm⁻¹). We note that a small amount CO will be adsorbed on top of single Pd atoms (Figure S3 in the ESI†). On a pure Pt surface, CO will tend to adsorb atop a cluster of atoms; this may also be seen in Fig. 3 (top-site adsorption, Raman shift ≈ 2070 cm⁻¹). As θ_Pt is increased, more Pt top sites and fewer Pd bridge sites become available. Meanwhile, electron transfer between Pd and Pt can also reduce the amount of CO at Pd bridge sites.^43,44 Therefore, the relative intensity of the 2070 cm⁻¹ band increases and that of the 1950 cm⁻¹ band decreases. Thus, Fig. 3 confirms very well the change in θ_Pt.

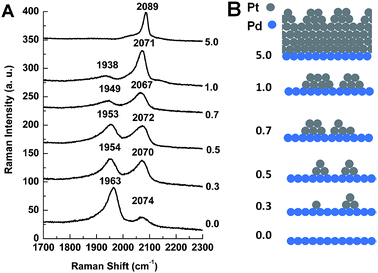Fig. 3 (A) SERS spectra of CO adsorbed on 55 nm Au@Pd@Pt NPs with 2 monolayers of Pd and different θ_Pt in a CO-saturated 0.1 M aqueous solution of HClO₄ at 0 V; (B) our proposed model of the surface of Au@Pd@Pt NPs having different θ_Pt.

The formation of Pt clusters may also be confirmed by changes in the frequency of these two adsorption peaks. As more and more Pt clusters form, the area covered by Pd bridge sites will be increasingly interrupted by Pt. The number of adjacent Pd bridge sites will be reduced, dipole–dipole coupling between CO molecules on adjacent Pd bridge sites will be reduced, and the frequency of the Pd bridge-site adsorption band will decrease.⁴³ Thus, Fig. 3 shows a red shift for the Pd bridge-site band at about 1950 cm⁻¹. When θ_Pt is increased from 0.0 to 0.3 for example, the frequency of the C–O stretching mode decreases from 1963 to 1954 cm⁻¹ (Fig. 3A) and this spectral change marks the transition from bimetallic to trimetallic NPs (Fig. 3B).The frequency changes observed for CO on top of Pt are even more interesting, as they appear to be quite complex. The greatest frequency jump, from 2071 to 2089 cm⁻¹, is seen along with the disappearance of the Pd bridge-bonded CO peak at 1938 cm⁻¹ when θ_Pt is increased from 1.0 to 5.0 (Fig. 3A). Here, another important transition is made: the Pd surface is still exposed when θ_Pt ≈ 1.0, indicating the Pt cluster structure, but it is completely covered when θ_Pt ≈ 5.0 (Fig. 3B). The other shifts seen for θ_Pt values between 0.3 and 1.0 may be due to changes in the configuration and extent of CO adsorption.

We now list three points which may help explain how the θ_Pt ≈ 0.5 structure is unique. First, Pd–Pt steps are formed when Pt islands are deposited onto Pd (DFT calculations were performed on these steps, and they will be discussed later). It would appear that the quantity and arrangement of these Pd–Pt steps are optimized when θ_Pt ≈ 0.5. Second, the redistribution of surface charge caused by partial electron transfer between Pd and Pt occurs due to their different work function. This can modify CO binding to surfaces where Pd and Pt atoms lie in close proximity to one another.⁴⁵ Third, the full width at half maximum (FWHM) of the CO atop Pt peak is three times larger when θ_Pt ≈ 0.5 (73 cm⁻¹) than it is at full coverage when θ_Pt ≈ 5.0 (23 cm⁻¹). The width of the band is at a maximum when θ_Pt ≈ 0.5, and this also indicates that the structure is unique.

Finally, we note that both the Pd bridge and Pt top-site CO peaks display a long, low-frequency tail. Samjeske et al.⁴⁶ observed a similar tail in connection with CO adsorbed on Pt terrace structures in the near vicinity of defects in a polycrystalline Pt electrode, and Alvarez et al.⁴⁷ observed a tail in connection with CO adsorbed on Pt–Pd steps. Similarly, our Au@Pd@Pt NP surfaces must possess some defects. We therefore suggest that the tail on the low frequency side of each peak is due to a structure which is the same as the one causing the peak, but in the near vicinity of defects where dipole–dipole coupling is reduced.

It will now be shown that the chemical and physical properties of our core–shell–cluster NPs are distinct from those obtained by other strategies for synthesizing trimetallic cluster NPs, which typically yield alloy properties.⁴⁸

Distinct activities toward the electrooxidation of formic acid

Linear voltammetry was used to investigate the effect of θ_Pt on the catalytic activity of Au@Pd@Pt NPs toward electrooxidation of formic acid. Fig. 4A shows that, with a fixed core size of 55 nm and a Pd-shell thickness of about 2 atomic layers, the catalytic activity depends remarkably on θ_Pt and is at a maximum when θ_Pt is about 0.5. This indicates that a synergistic effect occurs between the two metals. Yang and coworkers¹⁰ studied Pd and Pt separately, but did not look for a synergistic effect between them. Wieckowski^49,50 and Masel⁵¹ combined Pd and Pt, but on bulk metal surfaces which are not ideal for industrial applications. Feliu and coworkers³⁰ decorated Pt nanocubes with Pd adatoms and saw increased activity toward formic acid electrooxidation. Of these, our work is most similar to the Feliu group's work but we use Au NPs as a substrate for Pt islands on Pd in order to introduce strain and thereby further increase catalytic activity (the effect of the Au substrate will be discussed in more detail later).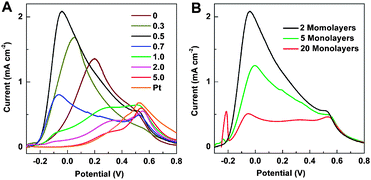

Fig. 4 (A) Linear voltammograms of 55 nm Au@Pd@Pt NPs with 2 monolayers of Pd and various θ_Pt, and 55 nm Au@Pt with θ_Pt ≈ 2, in a solution of 0.1 M HCOOH + 0.1 M H₂SO₄. The scanning rate was 10 mV s⁻¹. (B) Linear voltammograms of 55 nm Au@Pd@Pt NPs with θ_Pt fixed to be about 0.5 but different Pd shell thickness. The scanning rate was 10 mV s⁻¹.

It should be emphasized that the onset potential of formic acid oxidation is about −0.23 V and the current peak potential is about −0.05 V. These values are much more negative than the corresponding values obtained by Feliu's group³⁰ and Yang's group,¹⁰ and other groups that use monometallic and bimetallic nanostructures,^12,52–55 indicating a much higher catalytic activity through construction of our core–shell–cluster NPs.

According to Grozovski et al., the dehydration step of formic acid oxidation will take place in a potential region where little hydrogen is adsorbed.^56,57 In our case, the onset of hydrogen desorption and the onset of formic acid oxidation occur simultaneously at about −0.23 V (S4 in the ESI†). At about 0 V, hydrogen desorption is complete and this is one possible reason why catalytic activity reaches a maximum at about −0.05 V (S4 in the ESI†). In addition to possessing high catalytic activity, our Au@Pd@Pt NPs are stable beyond 2 h (see S5 in the ESI†). This is consistent with the literature, where it has been shown that Pd NPs have high catalytic activity but low stability while Pd NPs modified with Pt have both high activity and high stability.⁵⁸

The Au@Pd@Pt NPs show maximum catalytic activity when θ_Pt ≈ 0.5, which is to say that this Pt-cluster on Pd structure is optimal for the electrooxidation of formic acid. Our core–shell–cluster nanostructure is completely different from other bimetallic and trimetallic alloy/composite nanostructures because we can tune the proportion of the core, shell and cluster independently according to our needs. The other virtue of this method is that the syntheses are performed in aqueous solution without using a strong surfactant, so the NPs are easy to wash clean of any surfactant which may block their active sites.

It will then be of interest to examine the influence of the thickness of the Pd shell from 2 to 20 atomic layers with a fixed Au core size and a fixed θ_Pt. Fig. 4B shows that the electrooxidation activity of formic acid decreases dramatically with increasing shell thickness. The small anodic peak at −0.22 V is related to the desorption of hydrogen, and it is proportional to shell thickness;^59–61 we note that adsorbed species such as hydrogen, CO from the reduction of CO₂, ions and water may all have an influence on catalytic activity (see S4 in the ESI†).^56,62,63 The thickness-dependent catalytic activity toward electrooxidation of formic acid indicates that the interaction of the Pd overlayer with the Au core plays an important role: it can generate lateral strain in the Pd overlayer at the interface,^64–67 and this affects catalytic activity. The atomic radius of Pd is smaller than that of Au, and as a result, Pd has a more open structure when it grows on Au (i.e., the Pd atoms are further apart than they would otherwise be). Thus, tensile strain is created when the first few monolayers of Pd are deposited on the Au surface. As the thickness of the Pd shell increases up to five or more atomic layers, the tensile strain is released in those subsequent layers. As the open structure returns gradually to the normal surface structure, catalytic activity approaches that of a monometallic Pd NP.⁶⁴ Alternatively, the decrease in catalytic activity seen with increasing Pd shell thickness may be caused by changing electronic interactions between the Au core, Pd shell, and Pt clusters. Further research is needed to determine the relative importance of these potential mechanisms by which Pd shell thickness affects catalytic activity.

Adzic and co-workers found that Pd- or Pd₃Co-core Pt-shell NPs have higher activity toward the oxygen reduction reaction (ORR) than bare Pt NPs,³¹ and that the underlying material will influence the properties of subsequent Pt monolayers;⁶⁸ but our system offers an additional advantage in that the catalytic activity of Pd@Pt is further increased by the underlying Au core. Kolb and co-workers⁶⁹ have examined the electrooxidation of formic acid on a Pd modified Au(111) surface and found that peak currents did not improve much as the thickness of the Pd overlayer was increased from 1 to 5 atomic layers, despite the fact that the Au(111) substrate was completely inactive for formic acid oxidation under the experimental conditions used there. Strasser et al.⁷⁰ found that ORR activity can be tuned by the strain. Kibler et al.⁶⁴ found that more open Pd monolayers show high catalytic activity, while compression reduces the oxidation currents significantly. All of these results are consistent with ours.

We also synthesized core–shell–cluster structures possessing a nanocube, instead of a nanosphere, core. Au@Pd nanocubes were prepared according to Fan et al.,¹⁸ and Pt clusters were added as before. Fig. 5A shows that, again, maximum catalytic activity is achieved via the θ_Pt ≈ 0.5 structure.

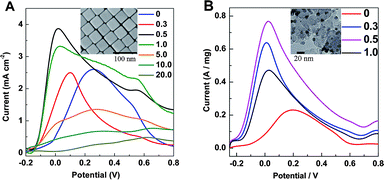Fig. 5 (A) Linear voltammograms were obtained from 40 nm Au@Pd@Pt nanocubes with 2 monolayers of Pd and various θ_Pt in a solution of 0.1 M HCOOH + 0.1 M H₂SO₄. (B) Linear voltammograms were obtained from 9 nm Ag@Pd@Pt NPs with 2 monolayers of Pd and various θ_Pt in a solution of 0.1 M HCOOH + 0.1 M H₂SO₄. For both, the scanning rate was 50 mV s⁻¹ and an SEM image is given in the inset.

In order to make the catalyst cheaper and therefore more applicable to an industrial setting, we reduced the size of the Au core from 55 to 16 nm (see S1 in the ESI†). We also prepared NPs with a 9 nm Ag core (see S2 in the ESI†). Both of these were successfully loaded onto carbon black (our procedure for this is described in ESI section S2†) and used as a catalyst for the electrooxidation of formic acid. As with the 55 nm Au@Pd@Pt NPs, they showed maximum catalytic activity when θ_Pt ≈ 0.5. Data for the 9 nm Ag@Pd@Pt NPs is shown in Fig. 5B. We note that NPs with a 9 nm Ag core, 2 atomic layers of Pd and a Pt loading such that θ_Pt ≈ 0.5 have a Ag : Pd : Pt molar ratio of about 50 : 10 : 1. We note also that a 55 nm particle diameter is in the ideal size range to provide high SERS activity for the mechanistic studies (5 or 10 to 120 nm^71,72) but we start to sacrifice SERS activity in favor of low cost when we move to a 16 or 9 nm diameter. Since the ideal θ_Pt is constant for different types of NPs, the Pt-on-Pd structure must have some specific position for the electrooxidation of formic acid.

SERS measurement and DFT calculations to study the mechanism of formic acid electrooxidation

Of central interest here is the synergistic effect of the special core–shell–cluster structure with an extremely small amount of Pt on the ultra-thin Pd overlayer, because neither the well-distributed Pt clusters nor the open structured Pd overlayer alone can exhibit such abnormally high catalytic activity. Since the above-mentioned electrochemical measurements were unable to reveal a detailed mechanism, a combination of spectroscopic and theoretical methods were employed to gain mechanistic information on this complex system at the atomic and molecular levels.

Since Au NPs provide long-range electromagnetic field enhancement, we may “borrow” SERS activity from the Au core (which lies beneath the Pd layers and the Pt clusters) and use it to examine species adsorbed on the surface of the NPs during electrooxidation of formic acid.^36,73–75Fig. 6A presents SERS spectra obtained from 55 nm Au@Pd@Pt NPs with 2 monolayers of Pd and θ_Pt ≈ 0.5 in an aqueous solution of formic acid. The peak at about 1844 cm⁻¹ is assigned to stretching of CO_ad in three-fold-hollow Pd shell sites, and the peak at about 2000 cm⁻¹ is assigned to stretching of linear-bonded CO_ad atop Pt clusters.⁷⁶ In the low frequency region, the 395 cm⁻¹ band corresponds to the Pd–C stretch and the 494 cm⁻¹ band corresponds to the Pt–C stretch. As explained above, the presence of a three-fold-hollow CO peak indicates that the coverage of CO on Pd is very low.

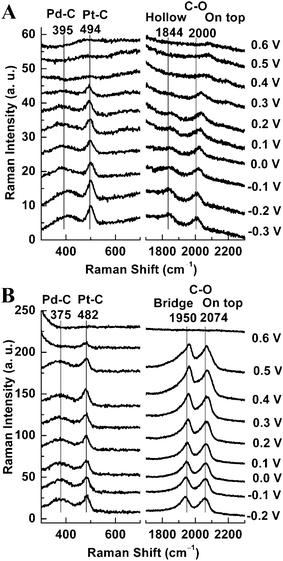Fig. 6 SERS spectra recorded on a GC electrode coated with 55 nm Au@Pd@Pt NPs having 2 monolayers of Pd and θ_Pt ≈ 0.5 in different solutions: (A) 0.1 M H₂SO₄ + 0.1 M HCOOH, and (B) CO-saturated 0.1 M H₂SO₄. Each potential is indicated in the figure.

For comparison, we also performed SERS measurements on the same NPs in a CO saturated solution without formic acid. As shown in Fig. 6B, the CO stretching frequencies are about 75–105 cm⁻¹ higher for CO_ad molecules in the saturated CO solution than they are for CO_ad molecules in the formic acid solution. In a Fourier transform infrared (FTIR) and SERS study of formic acid oxidation on Pt-group metals by Weaver and co-workers,^77,78 it was found that when the coverage of CO increases, the C–O stretching frequency increases because there are more dipole–dipole interactions between the CO molecules. We note, however, that the frequency of the 1844 cm⁻¹ band increases by ∼105 cm⁻¹ whereas the frequency of the 2000 cm⁻¹ band increases by only ∼75 cm⁻¹. Thus, it seems reasonable to attribute the frequency increase seen for the 2000 cm⁻¹ band to increased dipole–dipole coupling, but we believe an additional effect may be contributing to the 1844 cm⁻¹ band shift: a change in the preferred adsorption site from the Pd three-fold-hollow to the Pd bridge.

It should be noted that the SERS intensity of CO in these two systems are drastically different (see Fig. 6A and 6B), which indicate that the CO coverage in the HCOOH solution is much lower than that in the CO saturated solution. A much lower coverage of CO on the surface of our trimetallic NPs can greatly reduce active-site poisoning by CO, and leave more available for electrooxidation of formic acid. This is one of the reasons why our trimetallic NPs show much higher catalytic activity than other monometallic or bimetallic systems. Further evidence for the band assignments given above is provided in S3 of the ESI.†

Fig. 6A shows that CO was present at all potentials, yet Fig. 4A (black curve) shows that the catalytic activity was high throughout the potential range examined. There are three reasons for this. First, the surface coverage of CO is very low as indicated by low SERS intensity and low frequency Raman shifts (Fig. 6A). Second, CO is produced mainly on Pt (see S6 in the ESI†).^79–81 This is evidenced by the relative SERS intensities in Fig. 6: the Pd peak at ∼1844 cm⁻¹ is much weaker than the Pt peak at ∼2000 cm⁻¹ (Fig. 6A), whereas these two peaks are of similar intensity when the electrode is placed in a CO-saturated solution (Fig. 6B). Third, CO is oxidized to CO₂ at more positive potentials. CO₂ then leaves the surface, and more active sites become available for the adsorption and reaction of formic acid. The peak at about 1844 cm⁻¹ in Fig. 6A, for example, gradually disappears with increasing potential indicating three-fold-hollow Pd shell sites become more difficult to poison with CO.

In order to obtain a deep understanding of the electrochemical and the SERS results, and to clearly reveal the formic acid active sites and the CO-poisoned sites, total-energy DFT calculations were performed using the Vienna ab initio simulation package (VASP).⁸² Four possible CO adsorption/reaction sites are shown in Fig. 7, and the corresponding CO adsorption energies are provided in Table 1.

Table 1 DFT Results for the Energy of CO Adsorption on 55 nm Au@Pd@Pt NPs with Different Pd Shell Thicknesses and θ_Pt ≈ 0.5

Pd Shell Thickness	Energies for adsorption at the positions shown in Fig. 7 (eV)
	A	B	C	D
2 Monolayers of Pd	2.05	2.04	2.32	1.57
5 Monolayers of Pd	2.17	1.98	1.84	1.84

---

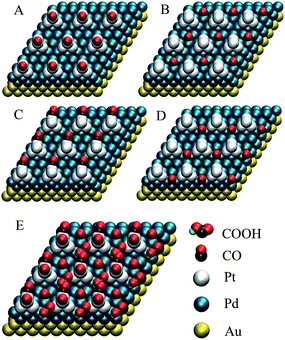Fig. 7 The atomic view of four different sites for adsorption/reaction: (A) a Pt cluster on-top site, (B) an isolated Pd hollow site, (C) a one Pt-atom and two Pd-atom mixed hollow site, (D) a two Pd-atom between two Pt clusters mixed hollow site; and (E) proposed adsorption model for CO on all four of the above sites.

For NPs with 2 monolayers of Pd, the CO adsorption energies in Table 1 can be divided into two distinct categories, high energy sites (A, B and C) and low energy sites (D). CO adsorption will be favored atop Pt clusters (A) and on isolated Pd hollow sites (B), which exist widely in ordinary Pt and Pd surfaces. It will also be favored on mixed hollow C-sites, which exist in most Pt/Pd bimetallic surfaces. The calculations in Table 1 show, however, that CO adsorption is rare on mixed hollow D-sites, which are thus free to catalyze the electrooxidation of formic acid. Fig. 4A shows that catalytic activity is maximum when θ_Pt ≈ 0.5, and the reason for this may now be understood: the number of mixed hollow D-sites will first increase and then decrease with increasing Pt coverage, reaching a maximum when θ_Pt ≈ 0.5.

For NPs with 5 monolayers of Pd, there are also two categories of adsorption energy: the high energy A and B sites, and the low energy C and D sites. The low energy sites are difficult to poison with CO, hence C and D are free for the electrooxidation of formic acid.

The DFT calculations also show that the CO adsorption energy for a given site, such as C or D, is dependent upon Pd shell thickness. Accordingly, the unusually high catalytic activity seen in our Au@Pd@Pt NPs must occur by a synergistic effect. So while the Au core can affect the Pd shell and Pt clusters (by opening their structures and by electron transfer),^64,83 and the Pd shell can affect the Pt clusters (by opening its structure and by electron transfer),^43,84 the Pt clusters can conversely alter the properties of their support (the adsorption energies for B and D sites given in Table 1 are different, though both of them are the same Pd hollow sites). Further DFT calculations indicate that the reaction intermediate COOH is adsorbed at the D-site with an orientation that greatly facilitates the direct oxidation of formic acid to CO₂ (see S7 in the ESI†).

According to Nørskov and co-workers,^85,86 adsorption energies and catalytic activities are greatly dependent on the d-band center. Changes in the position of the d-band center should therefore also be cited to explain why Au@Pd@Pt NPs with 2 monolayers of Pd and θ_Pt ≈ 0.5 have the highest catalytic activity. DFT calculations have shown that the electronic properties of a surface can be modified considerably by changing the nearest-neighbor distance, such as in pseudomorphic overlayers, and that this effect is related to a shift in the d-band center.^31,64 In this regard, the d-band center of Pd is not only modified by the Au support, but also by the Pt overlayer in our system. The lower the d-band center, the weaker the metal–adsorbate binding strength during oxidation and the more negative the oxidation potential.⁸⁷ This is another possible reason why the onset potential of formic acid oxidation (−0.23 V) and the current peak potential (−0.05 V) are so negative for Au@Pd@Pt NPs with 2 monolayers of Pd and θ_Pt ≈ 0.5.

The combination of spectroscopic and DFT results provide much information about the origin of the unusually high activity of Au@Pd@Pt NPs with an ultrathin Pd shell and very low Pt cluster coverage. Pt top sites (A) are quite active for the dissociation of formic acid,¹ but simultaneously prone to CO adsorption (Table 1). In contrast, isolated Pd hollow sites (B) do not catalyze the dissociation of formic acid well,^1,40 but SERS spectra obtained from Au@Pd NPs show that the Pd surface is relatively free from poisoning by CO (see S6 in the ESI†) although some CO adsorption does occur (Table 1). The trimetallic NPs described in this work are ideal, however, because they exhibit high catalytic activity and the two Pd atoms between two Pt cluster mixed hollow D-sites (which we believe to be most active) have a low tendency toward CO poisoning. The D-site adsorption/reaction characteristics are more favorable for the electrooxidation of formic acid in the case of the Au@Pd@Pt NPs with 2 monolayers of Pd (Fig. 4B, black curve) than they are in the case of the Au@Pd@Pt with 5 monolayers of Pd (Fig. 4B, green curve) because the Pd structure is more open, because CO poisoning occurs to a lesser extent, and possibly because of electronic effects as well. Thus we have tuned the composition of the NPs, optimizing their structure for the electrooxidation of formic acid.

The extremely high electrooxidation activity is most likely due to synergistic morphological and electronic effects at the mixed hollow D-sites. The structure at these active sites is determined not only by Pt and Pd, but also by the underlying Au substrate. The synergistic effects of our trimetallic structures could be propitious to the electrooxidation of formic acid, either directly or through the formate pathway.^81,88,89 The Pt coverage on Pd should be θ_Pt ≈ 0.5 to maximize the number of mixed hollow D-sites and possibly also tune the position of the d-band center, therefore optimizing the catalytic activity.

Conclusions

We have rationally synthesized Au@Pd@Pt NPs using the atomic radius, cohesive energy, and electronegativity of these three metals to initiate different growth modes. Au NPs coated with two atomic layers of Pd, and Pt clusters such that θ_Pt ≈ 0.5, possess the highest catalytic activity for electrooxidation of formic acid when compared to other nanostructures such as Au@Pd NPs, Au@Pt NPs and previous bimetallic systems using massive electrodes.^{10,12,52,53,90–92} An increase in the loading of Pd beyond 2 atomic layers and Pt beyond θ_Pt ≈ 0.5 will actually decrease catalytic activity, a phenomenon which is quite interesting scientifically. The combination of electrochemical, spectroscopic and DFT studies presented in this work reveal that our trimetallic nanostructure has electronic properties and a surface morphology which are uniquely suited for catalysis.

The high catalytic activity that we have demonstrated for Au@Pd@Pt NPs with only two atomic layers of Pd and a submonolayer quantity of Pt makes them a promising new electrode material for commercial fuel cells. In addition, the Au core could be replaced by Ag, which is structurally similar but much cheaper, to achieve enhanced catalytic activity by the same synergistic effect. Given the ease with which NPs may be prepared, together with the availability of diverse core, shell and cluster materials (metals or even oxides), there is tremendous potential for generating a myriad of nanomaterials by the present means. These nanomaterials are appropriate for use in fuel cells and other electrochemical and catalytic process applications, as well as for use in sensors.

Acknowledgements

This work was supported by the Major International Collaborative Research Project of NSFC (No. 20620130427), the International Scientific and Technological Cooperation Projects of MOST (No. 2007DFC40440), the 973 Program (Nos. 2009CB930703 and 2007CB815303), ENS and CNRS (UMR 8640, LIA XiamENS).

Notes and references

1. X. W. Yu and P. G. Pickup, J. Power Sources, 2008, 182, 124.
2. M. A. Mahmoud, C. E. Tabor, M. A. El-Sayed, Y. Ding and Z. L. Wang, J. Am. Chem. Soc., 2008, 130, 4590.
3. V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. F. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241.
4. S. Uhm, H. J. Lee, Y. Kwon and J. Lee, Angew. Chem., Int. Ed., 2008, 47, 10163.
5. D. Strmcnik, K. Kodama, D. van der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2009, 1, 466.
6. S. Alayoglu, A. U. Nilekar, M. Mavrikakis and B. Eichhorn, Nat. Mater., 2008, 7, 333.
7. F. Tao, M. E. Grass, Y. W. Zhang, D. R. Butcher, J. R. Renzas, Z. Liu, J. Y. Chung, B. S. Mun, M. Salmeron and G. A. Somorjai, Science, 2008, 322, 932.
8. H. Abe, F. Matsumoto, L. R. Alden, S. C. Warren, H. D. Abruna and F. J. DiSalvo, J. Am. Chem. Soc., 2008, 130, 5452.
9. A. Lopez-Cudero, F. J. Vidal-Iglesias, J. Solla-Gullon, E. Herrero, A. Aldaz and J. M. Feliu, J. Electroanal. Chem., 2009, 637, 63.
10. H. J. Lee, S. E. Habas, G. A. Somorjai and P. D. Yang, J. Am. Chem. Soc., 2008, 130, 5406.
11. N. Kristian, Y. S. Yan and X. Wang, Chem. Commun., 2008, 353.
12. W. J. Zhou and J. Y. Lee, Electrochem. Commun., 2007, 9, 1725.
13. P. N. Bartlett and S. Guerin, Anal. Chem., 2003, 75, 126.
14. M. Grzelczak, J. Perez-Juste, F. J. G. de Abajo and L. M. Liz-Marzán, J. Phys. Chem. C, 2007, 111, 6183.
15. A. Kowal, M. Li, M. Shao, K. Sasaki, M. B. Vukmirovic, J. Zhang, N. S. Marinkovic, P. Liu, A. I. Frenkel and R. R. Adzic, Nat. Mater., 2009, 8, 325.
16. C. J. Zhong, J. Luo, P. N. Njoki, D. Mott, B. Wanjala, R. Loukrakpam, S. Lim, L. Wang, B. Fang and Z. C. Xu, Energy Environ. Sci., 2008, 1, 454.
17. S. Maksimuk, S. C. Yang, Z. M. Peng and H. Yang, J. Am. Chem. Soc., 2007, 129, 8684.
18. F. R. Fan, D. Y. Liu, Y. F. Wu, S. Duan, Z. X. Xie, Z. Y. Jiang and Z. Q. Tian, J. Am. Chem. Soc., 2008, 130, 6949.
19. J. W. Hu, J. F. Li, B. Ren, D. Y. Wu, S. G. Sun and Z. Q. Tian, J. Phys. Chem. C, 2007, 111, 1105.
20. B. Lim, H. Kobayashi, T. Yu, J. G. Wang, M. J. Kim, Z. Y. Li, M. Rycenga and Y. Xia, J. Am. Chem. Soc., 2010, 132, 2506.
21. A. Roudgar and A. Gross, Surf. Sci., 2004, 559, L180.
22. Z. Y. Bai, L. Yang, L. Li, J. Lv, K. Wang and J. Zhang, J. Phys. Chem. C, 2009, 113, 10568.
23. Y. W. Rhee, S. Y. Ha and R. I. Masel, J. Power Sources, 2003, 117, 35.
24. O. Manuel and I. Enrique, Angew. Chem., Int. Ed., 2009, 48, 4800.
25. C. M. Miesse, W. S. Jung, K. J. Jeong, J. K. Lee, J. Lee, J. Han, S. P. Yoon, S. W. Nam, T. H. Lim and S. A. Hong, J. Power Sources, 2006, 162, 532.
26. B. Ren, X. F. Lin, Y. X. Jiang, P. G. Cao, Y. Xie, Q. J. Huang and Z. Q. Tian, Appl. Spectrosc., 2003, 57, 419.
27. L. Xiao, L. Zhuang, Y. Liu, J. T. Lu and H. D. Abruna, J. Am. Chem. Soc., 2009, 131, 602.
28. O. Ghodbane, L. Roue and D. Belanger, Chem. Mater., 2008, 20, 3495.
29. X. G. Li and I. M. Hsing, Electrochim. Acta, 2006, 51, 3477.
30. F. J. Vidal-Iglesias, J. Solla-Gullón, E. Herrero, A. Aldaz and J. M. Feliu, Angew. Chem., Int. Ed., 2010, 49, 6998.
31. J. X. Wang, H. Inada, L. J. Wu, Y. M. Zhu, Y. M. Choi, P. Liu, W. P. Zhou and R. R. Adzic, J. Am. Chem. Soc., 2009, 131, 17298.
32. D. R. Lide, CRC Handbook of Chemistry and Physics. 87 ed., Boca Raton, 2007.
33. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter, 1992, 46, 16067.
34. G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter, 1995, 51, 4014.
35. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter, 1989, 40, 3616.
36. Z. Q. Tian, B. Ren, J. F. Li and Z. L. Yang, Chem. Commun., 2007, 3514.
37. G. Frens, Nat. Phys. Sci., 1973, 241, 20.
38. J. W. Hu, Y. Zhang, J. F. Li, Z. Liu, B. Ren, S. G. Sun, Z. Q. Tian and T. Lian, Chem. Phys. Lett., 2005, 408, 354.
39. S. E. Habas, H. Lee, V. Radmilovic, G. A. Somorjai and P. Yang, Nat. Mater., 2007, 6, 692.
40. H. Miyake, T. Okada, G. Samjeske and M. Osawa, Phys. Chem. Chem. Phys., 2008, 10, 3662.
41. F. M. Hoffmann, Surf. Sci. Rep., 1983, 3, 107.
42. I. V. Yudanov, R. Sahnoun, K. M. Neyman, N. Rosch, J. Hoffmann, S. Schauermann, V. Johanek, H. Unterhalt, G. Rupprechter, J. Libuda and H. J. Freund, J. Phys. Chem. B, 2003, 107, 255.
43. C. Wang, D. van der Vilet, K. C. Chang, H. D. You, D. Strmcnik, J. A. Schlueter, N. M. Markovic and V. R. Stamenkovic, J. Phys. Chem. C, 2009, 113, 19365.
44. N. Todoroki, H. Osano, T. Maeyama, H. Yoshida and T. Wadayama, Appl. Surf. Sci., 2009, 256, 943.
45. C. Wang, B. Peng, H. N. Xie, H. X. Zhang, F. F. Shi and W. B. Cai, J. Phys. Chem. C, 2009, 113, 13841.
46. G. Samjeske, K. Komatsu and M. Osawa, J. Phys. Chem. C, 2009, 113, 10222.
47. D. S. Strmcnik, D. V. Tripkovic, D. van der Vliet, K. C. Chang, V. Komanicky, H. You, G. Karapetrov, J. Greeley, V. R. Stamenkovic and N. M. Markovic, J. Am. Chem. Soc., 2008, 130, 15332.
48. D. Ferrer, A. Torres-Castro, X. Gao, S. Sepulveda-Guzman, U. Ortiz-Mendez and M. Jose-Yacaman, Nano Lett., 2007, 7, 1701.
49. P. Waszczuk, T. M. Barnard, C. Rice, R. I. Masel and A. Wieckowski, Electrochem. Commun., 2002, 4, 732.
50. P. Waszczuk, T. M. Barnard, C. Rice, R. I. Masel and A. Wieckowski, Electrochem. Commun., 2002, 4, 599.
51. C. Rice, S. Ha, R. I. Masel and A. Wieckowski, J. Power Sources, 2003, 115, 229.
52. N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Science, 2007, 316, 732.
53. V. Mazumder and S. H. Sun, J. Am. Chem. Soc., 2009, 131, 4588.
54. M. J. Llorca, J. M. Feliu, A. Aldaz and J. Clavilier, J. Electroanal. Chem., 1994, 376, 151.
55. M. Zhao, C. Rice, R. I. Masel, P. Waszczuk and A. Wieckowski, J. Electrochem. Soc., 2004, 151, A131.
56. V. Grozovski, V. Climent, E. Herrero and J. M. Feliu, Phys. Chem. Chem. Phys., 2010, 12, 8822.
57. V. Grozovski, V. Climent, E. Herrero and J. M. Feliu, ChemPhysChem, 2009, 10, 1922.
58. S. Uhm, H. J. Lee and J. Lee, Phys. Chem. Chem. Phys., 2009, 11, 9326.
59. P. N. Bartlett and J. Marwan, Phys. Chem. Chem. Phys., 2004, 6, 2895.
60. P. N. Bartlett and J. Marwan, Chem. Mater., 2003, 15, 2962.
61. L. A. Kibler, A. M. El-Aziz and D. M. Kolb, J. Mol. Catal. A: Chem., 2003, 199, 57.
62. F. J. Vidal-Iglesias, J. Solla-Gullon, E. Herrero, A. Aldaz and J. M. Feliu, J. Appl. Electrochem., 2006, 36, 1207.
63. G. Q. Lu, A. Crown and A. Wieckowski, J. Phys. Chem. B, 1999, 103, 9700.
64. L. A. Kibler, A. M. El-Aziz, R. Hoyer and D. M. Kolb, Angew. Chem., Int. Ed., 2005, 44, 2080.
65. A. Schlapka, M. Lischka, A. Gross, U. Kasberger and P. Jakob, Phys. Rev. Lett., 2003, 91, 016101.
66. A. Roudgar and A. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 4.
67. M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819.
68. M. H. Shao, T. Huang, P. Liu, J. Zhang, K. Sasaki, M. B. Vukmirovic and R. R. Adzic, Langmuir, 2006, 22, 10409.
69. M. Baldauf and D. M. Kolb, J. Phys. Chem., 1996, 100, 11375.
70. P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Nat. Chem., 2010, 2, 454.
71. P. P. Fang, J. F. Li, Z. L. Yang, L. M. Li, B. Ren and Z. Q. Tian, J. Raman Spectrosc., 2008, 39, 1679.
72. M. Moskovits, J. Raman Spectrosc., 2005, 36, 485.
73. K. N. Heck, B. G. Janesko, G. E. Scuseria, N. J. Halas and M. S. Wong, J. Am. Chem. Soc., 2008, 130, 16592.
74. N. Pázos-Pérez, W. Ni, A. Schweikart, R. A. Alvarez-Puebla, A. Fery and L. M. Liz-Marzán, Chem. Sci., 2010, 1, 174.
75. M. F. Cardinal, B. Rodriguez-Gonzalez, R. A. Alvarez-Puebla, J. Perez-Juste and L. M. Liz-Marzán, J. Phys. Chem. C, 2010, 114, 10417.
76. S. Z. Zou and M. J. Weaver, Anal. Chem., 1998, 70, 2387.
77. S.-C. Chang, Y. Ho and M. J. Weaver, Surf. Sci., 1992, 265, 81.
78. M. F. Mrozek, H. Luo and M. J. Weaver, Langmuir, 2000, 16, 8463.
79. M. Arenz, V. Stamenkovic, T. J. Schmidt, K. Wandelt, P. N. Ross and N. M. Markovic, Phys. Chem. Chem. Phys., 2003, 5, 4242.
80. J. Rodriguez-Lopez and A. J. Bard, J. Am. Chem. Soc., 2010, 132, 5121.
81. G. Samjeske and M. Osawa, Angew. Chem., Int. Ed., 2005, 44, 5694.
82. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
83. A. M. El-Aziz, L. A. Kibler and D. M. Kolb, Electrochem. Commun., 2002, 4, 535.
84. A. M. El-Aziz, R. Hoyer, L. A. Kibler and D. M. Kolb, Electrochim. Acta, 2006, 51, 2518.
85. J. K. Nørskov, T. Bligaard, B. Hvolbaek, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163.
86. J. Greeley, J. K. Nørskov and M. Mavrikakis, Annu. Rev. Phys. Chem., 2002, 53, 319.
87. H. X. Zhang, C. Wang, J. Y. Wang, J. J. Zhai and W. B. Cai, J. Phys. Chem. C, 2010, 114, 6446.
88. Y. X. Chen, M. Heinen, Z. Jusys and R. B. Behm, Angew. Chem., Int. Ed., 2006, 45, 981.
89. Y. X. Chen, S. Ye, M. Heinen, Z. Jusys, M. Osawa and R. J. Behm, J. Phys. Chem. B, 2006, 110, 9534.
90. I. S. Park, K. S. Lee, J. H. Choi, H. Y. Park and Y. E. Sung, J. Phys. Chem. C, 2007, 111, 19126.
91. X. L. Ji, K. T. Lee, R. Holden, L. Zhang, J. J. Zhang, G. A. Botton, M. Couillard and L. F. Nazar, Nat. Chem., 2010, 2, 286.
92. Q. Yuan, Z. Y. Zhou, J. Zhuang and X. Wang, Chem. Commun., 2010, 46, 1491.

---

Footnote

† Electronic supplementary information (ESI) available: additional images, experimental details, data for the verification of band assignments, CVs, chronoamperometric curves, SERS spectra of formate adsorbed on Au@Pd NPs, and DFT calculation results. See DOI: 10.1039/c0sc00489h

---