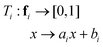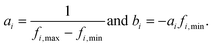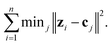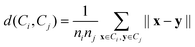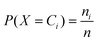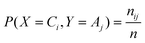Identification of fluid and substrate chemistry based on automatic pattern recognition of stains†
Namwon
Kim
a,
Zhenguo
Li
b,
Cedric
Hurth
c,
Frederic
Zenhausern
c,
Shih-Fu
Chang
b and
Daniel
Attinger
*d
aDepartment of Mechanical Engineering, Columbia University, New York, NY, 10027, USA
bDepartment of Electrical Engineering, Columbia University, New York, NY, 10027, USA
cCenter for Applied Nanobioscience and Medicine, College of Medicine Phoenix, University of Arizona, Phoenix, AZ 85004, USA
dDepartment of Mechanical Engineering, Iowa State University, Ames, IA, 50011, USA. E-mail: Attinger@iastate.edu
First published on 31st October 2011
Abstract
This study proposes that images of stains from 100-nanolitre drops can be automatically identified as signatures of fluid composition and substrate chemistry, for e.g. rapid biological testing. Two datasets of stain images are produced and made available online, one with consumable fluids, and the other with biological fluids. Classification algorithms are used to identify an unknown stain by measuring its similarity to representative examples of predefined categories. The accuracy ranges from 80 to 94%, compared to an accuracy by random assignment of 3 to 4%. Clustering algorithms are also applied to group unknown stain images into a number of clusters each likely to correspond to similar combinations of fluids and substrates. The clustering accuracy ranges from 62 to 80%, compared to an accuracy by random assignment of 3 or 4%. The algorithms were also remarkably accurate at determining the presence or absence of biotin and streptavidin respectively in the liquid and on the glass, the salt composition, or the pH of the solution.
Introduction
Pattern recognition broadens its application in various fields by substituting routine work requiring human senses such as sight, hearing, taste, touch and smell. Specifically developed pattern recognition and machine vision techniques are widely deployed in manufacturing assembly lines for automatic defect detection, in public safety and forensics for recognizing individuals on the basis of fingerprints,1 face,2 voice3 and handwriting.4 Other applications include food analysis5–8 and environmental monitoring9 for identifying physical and chemical data10 using sensor arrays such as electronic noses and tongue.When a drop of a complex fluid dries on a solid substrate, it leaves a stain, which is a complex signature of the drying conditions, of the morphology and chemistry of the substrate and of the composition of the fluid. The study of formation of patterns during the drying of small liquid droplets is of interest to biotechnology11–16 and materials science.17–19 Recent studies on the self-assembly of colloidal solutions of nanoparticles20,21 explained how some typical stains assume typical shapes such as a peripheral ring, a central bump or a uniform deposit. The structure of the stain was shown to be determined by the relative role of three convective transport phenomena involved in the deposition of the nanoparticles on the solid surface, i.e. the normal flow caused by electrostatic and Van der Waals forces, the radial flow caused by the maximum evaporation rate at the contact line,22 and the Marangoni recirculation caused by surface tension gradient at the air-liquid interface.23 The staining process can be parallelized and occurs within a few seconds because of Marangoni convection coupled with receding of the initial wetting line21 for sub-microlitre drops. A wealth of complex patterns appears in a reproducible manner in stains of fluids and substrates of controlled chemistry, showing multiple length scales, specific periodicity and features like lines, rings, crystals, and various grain sizes.16 Manual inspection of these features has been shown to provide information on the liquid and substrate chemistry.16,24 However, manual identification is tedious and expensive, especially when a lot of images are required to be identified. More critically, the results could be unreliable because of large and unpredictable variations of human factors. Automated identification such as pattern recognition can play a significant role in crime scene analysis and disease diagnosis, which are currently conducted manually by human experts. In contrast to manual identification, the pattern recognition approach is fast, purely data-driven, and not subject to human bias.25
The study presented here tests two hypotheses: (1) algorithms trained with existing data linking stain morphology to liquid and substrate chemistry can identify the liquid and substrate chemistry of an unknown stain; and (2) automated pattern recognition methods can group stains in a way that discriminates between specific combinations of liquid and substrate chemistry. The principle of the pattern recognition algorithms used in this study is as follows: they first perform automatic localization (or cropping) of the stain as a region of interest in the image, then extraction and computation of descriptive features, that are expressed quantitatively as a row vector f = [αfC, βfL, γfG, εfS]. This vector is assembled from four discriminative feature vectors, with relative weights expressed by α,β,γ, and ε. These feature vectors characterize the color distribution26 as fC, the local binary patterns (LBP)27 as fL, the Gabor wavelet28 pattern as fG, and the relative stain size as fS (see more details in the Methods section). Finally, two specific machine learning techniques are applied, a classification technique to test hypothesis (1), and a clustering technique to test hypothesis (2). Classification is performed by supervised pattern recognition algorithms that compare stain patterns in question with a set of training patterns of which the liquid/substrate category is known, computing the distance between the vector f of an unknown stain with vectors representing labeled stains, and assigning the unknown stain to the class of labeled stains that minimize that distance. Clustering uses unsupervised pattern recognition algorithms to identify patterns common to several images in the stain dataset and group similar stains into a manually determined number of clusters (or classes) without labeled data, such that each cluster corresponds to a distinct visual pattern. Two comprehensive collections of microscopic stain images were constructed from 100 nL drops of consumable and biological fluids to test pattern recognition algorithms. The first dataset contains 480 stain images from 24 consumable fluids (24 classes) such as beer, juice, liquor, milk, red wine, and soda, all deposited on clean glass slides. For each fluid, 20 stains were produced. The second dataset includes 600 stain images from 8 biological fluids (8 classes) such as 10 mM phosphate buffer made from three different ratii of K2HPO4 and KH2PO4, 20 mM phosphate buffer with pH values obtained from three different concentrations of citric acid, a solution of 0.01 mM potassium hydroxide and pure water. All fluids were deposited on two different types of glass slides, clean or coated with streptavidin, which resulted in 16 classes as described in the Methods section. The number of classes was doubled again (32 classes) by adding biotin to each solution. However, pure water on both clean and streptavidin glasses (2 classes) did not generate any stains, thus 30 classes were established for the biological fluids. For both datasets, the drying conditions and the substrate morphology were kept constant. For the sake of comparison with other pattern recognition methods, the two datasets of original stain pictures have been made available online.29
Methods
Fluid preparation
Consumable fluids including beers (Budweiser® Lager, Corona® Extra, Guinness® Extra Stout, Heineken® Lager, and Tsingtao® Lager), juices (Tropicana® Grape, Tropicana® Lemonade, Tropicana® Orange No Pulp, and Campbell's® Tomato), liquor (Disaronno® Originale Amaretto), milks (Horizon® 1% Low Fat, Horizon® 2% Reduced Fat, Horizon® Chocolate, Horizon® Fat Free, Silk® Soy, Horizon® Strawberry, and Horizon® Whole), red wines (2007 Chateau de Castelneau from Bordeaux, France, Merlot, 2008 Liberty School from Paso Robles, CA, USA, Syrah, and 2008 Graham Beck from Franschhoek, South Africa, Cabernet Sauvignon), and sodas (Coca Cola® Classic, Diet Coke®, Dr Pepper®, and Fanta® Orange) were purchased from local stores. The fluids were used no later than 2 hours after opening of the original containers. For the biological fluids, a series of aqueous buffer solutions were prepared using biotechnology performance certified-grade water (Sigma-Aldrich W3513, Saint-Louis, MO). A first subset consists of phosphate buffer (PB) solutions prepared to a final concentration of 10 mM using three different volume ratii of K2HPO4 and KH2PO4 (Sigma-Aldrich, Saint-Louis, MO) calculated according to the Henderson-Hasselbach formula to yield respective pH values of 6.03, 7.05, and 7.98 as checked by a pH meter (Acorn ph 6, Oakton Instruments, Vernon Hills, IL) calibrated with NIST standard solutions of pH = 4.00 and 7.00. The second subset of solutions consists of McIlvaine buffers, i.e. a mixture of 20 mM K2HPO4 and 15, 6.7 or 1.7 mM citric acid. This yields final pH values of 4.42, 6.19, and 7.64 respectively, as checked using a freshly calibrated pH meter. The final subset of solutions consists of a 10−5 M KOH solution, and the control, biotechnology performance certified-grade water, to attest of the absence of parasite particles in all solutions prepared. A similar series of biotin-containing solutions was prepared by dissolving biotin powder (Pierce Biotechnology, Inc. 29129, Rockford, IL) to a final concentration of 1.32 mM. All solutions were filtered using a syringe filter with Nylon membranes with 0.2 μm pores (Pall Acrodisc-25, Port Washington, NY) to remove all dust particles and undissolved buffer or biotin crystals.Glass slides preparation and droplet deposition
Microscope glass slides (12-544-1, Fisher Scientific, Pittsburgh, PA) were cleaned by immersion in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume mixture of sulfuric acid (H2SO4) and 30% hydrogen peroxide (H2O2) for 2 minutes, then rinsed extensively with filtered deionized water, and blown dry with compressed nitrogen gas in a class 1,000 cleanroom. To reduce wettability for deposition of the red wine drops, glass slides rinsed with filtered deionized water and dried with a stream of nitrogen gas were used. Streptavidin-coated glass slides (SMS, Arrayit Corporation, Sunnyvale, CA) were also rinsed with filtered deionized water, and subsequently dried with a stream of filtered nitrogen. Then, 0.1 μL droplets were deposited on the glass slide using recently calibrated micropipettes (0.1–2.5 μL, Eppendorf, Hauppauge, NY and P2, Gilson, Inc., Middleton, WI) by making slight contact between the surface and the liquid protruding from the pipette tip and subsequently pulling the micropipette away from the surface. The pipetting accuracy was determined by measuring the area occupied by 20 spots of a solution made of 1.32 mM biotin in water relative to the entire image field of view. This solution was chosen because it corresponded to one of the largest spreads of all solutions tested while still leaving a residue dense enough to be easily distinguished from the rest of the surface. The dried residue area was approximated by a box stretched to fit the residue and the area was measured by software (ImageJ, NIH, Bethesda, MD) and normalized to the entire image area. The area averaged at 7.5% of the entire field of view with a standard deviation of 0.8%. These numbers do not only reflect manual pipetting errors but also local differences in the glass surface. The slides were arrayed at room temperature of 20–23 °C with a relative humidity (RH) of 20–50% and immediately placed in a desiccator filled with anhydrous calcium chloride (CaCl2) or calcium sulfate (CaSO4) powders where they were allowed to dry for 24 h before imaging.
1 volume mixture of sulfuric acid (H2SO4) and 30% hydrogen peroxide (H2O2) for 2 minutes, then rinsed extensively with filtered deionized water, and blown dry with compressed nitrogen gas in a class 1,000 cleanroom. To reduce wettability for deposition of the red wine drops, glass slides rinsed with filtered deionized water and dried with a stream of nitrogen gas were used. Streptavidin-coated glass slides (SMS, Arrayit Corporation, Sunnyvale, CA) were also rinsed with filtered deionized water, and subsequently dried with a stream of filtered nitrogen. Then, 0.1 μL droplets were deposited on the glass slide using recently calibrated micropipettes (0.1–2.5 μL, Eppendorf, Hauppauge, NY and P2, Gilson, Inc., Middleton, WI) by making slight contact between the surface and the liquid protruding from the pipette tip and subsequently pulling the micropipette away from the surface. The pipetting accuracy was determined by measuring the area occupied by 20 spots of a solution made of 1.32 mM biotin in water relative to the entire image field of view. This solution was chosen because it corresponded to one of the largest spreads of all solutions tested while still leaving a residue dense enough to be easily distinguished from the rest of the surface. The dried residue area was approximated by a box stretched to fit the residue and the area was measured by software (ImageJ, NIH, Bethesda, MD) and normalized to the entire image area. The area averaged at 7.5% of the entire field of view with a standard deviation of 0.8%. These numbers do not only reflect manual pipetting errors but also local differences in the glass surface. The slides were arrayed at room temperature of 20–23 °C with a relative humidity (RH) of 20–50% and immediately placed in a desiccator filled with anhydrous calcium chloride (CaCl2) or calcium sulfate (CaSO4) powders where they were allowed to dry for 24 h before imaging.
Image acquisition
The images of the stains from consumable fluids shown in Fig. 1 were acquired using an inverted microscope (IX 71, Olympus, Center Valley, PA) equipped with a 2X objective (UIS2 PLN, NA = 0.06, WD = 5.8 mm, Olympus) and a color complementary metal oxide semiconductor (CMOS) camera (PL-A776, PixeLINK, Ottawa, ON, Canada) under bright field transillumination from a halogen lamp (U-LH100L-3, Olympus) through frost (LP453900, Olympus) and day light filters (9-U115). The acquired image with 2,040 × 1,536 pixel resolution at 20 ms exposure time resulted in a picture scale of 1.61 μm/pixel. Images of the stains from biological fluids were acquired using a Nikon Eclipse Ti-U inverted microscope equipped with a Nikon 2X objective (Plan Achromat UW, Nikon, NA = 0.06, WD = 7.5 mm) and a color CMOS camera (PL-E425CU, PixeLINK, Ottawa, ON, Canada). The acquired image resolution was set to 2,040 × 1,536 pixels with a 20 ms exposure time. Calibration with an etched glass ruler produced a calculated resolution of 1.03 μm/pixel. The intensity of the incident light (100 W Halogen) was adjusted to deliver 90 μW at 560 nm as measured by a 9 mm diameter silicon photodiode sensor (S130C, Thorlabs, Newton, NJ).Preprocessing of images and stains
The automatic localization of the stain was performed as shown in Fig. 2a, where the region containing the stain was cropped into a rectangle slightly larger than the stain to reduce the adverse effect of irrelevant background. Raw input images were then converted into grayscale and binary formats, sequentially. All the holes in the inverted images were filled up to have complete objects and an object of the largest area was treated as a stain. A bounding box was fitted to this area and the area of the stain was cropped from the original image with an offset on all sides in order to ensure the entire stain was selected. This cropped image was then resized to a 256 × 256 pixel image. Complete sets of the cropped stain images from consumable and biological fluids are shown in Fig. 1 and Fig. 4.Feature extraction: color, LBP, gabor wavelet and combined features
This section explains how a stain is described by a combined feature vector f = [αfC, βfL, γfG, εfS], where fC, fL, fG, and fS are row vectors representing respectively the color features, local binary patterns, Gabor features and size of the stain.Color features were described by the vector fC. Color features are among the simplest yet extensively used low-level features for content-based image analysis. They are robust against noise, resolution, orientation and resizing, although they convey little semantic meaning. The color feature of an image can be captured by its pixel distribution (histogram), in some color space. Here, we adopt the 3-component YCbCr color space which is perceptually more meaningful than the original RGB space. For each color channel, i.e., Y, Cb, or Cr, we first compute a pixel histogram (see Fig. 2b), and then calculate its mean, standard deviation, skew, energy, and entropy. Consequently, each of the three color components is represented by five features, so that fC is a 15 × 1 vector.26 The range of each dimension was normalized linearly to [0, 1] in order to balance the importance among each feature.
Local binary patterns (LBP) are represented by the vector fL. LBP is a popular texture operation which labels the pixels of an image by thresholding its neighborhood with the gray level value of the center pixel.27 Each pixel is associated with a sequence of binary number, and the histogram of the decimal numbers that correspond to the binary sequence of these binary numbers is taken as the LBP features for the image. For example, if a neighborhood of 8 pixels is used, as in the consumable fluid dataset, each center pixel is assigned with a sequence of 8 binary numbers, and the histogram will be of length 28 = 256. One example of LBP with 3 × 3 neighborhoods (8 pixels) and uniform pattern is shown in Fig. 1c. If a neighborhood of 16 pixels is used, as in the biological fluid dataset, the histogram is of length 216 = 65,536. To reduce the length of the feature vector, and more importantly, to implement rotation-invariant descriptor, patterns that typically reflect noise, from e.g. a uniform background, are removed from the histogram. The size of the vector fL used in the calculations was 10 × 1 for the consumable fluid dataset and 243 × 1 for the biological fluid dataset.
 | ||
| Fig. 1 Stains of consumable fluids show a wealth of colors and patterns that can be used for identifying the fluid. Fluids are: (Beers: a1–5) Budweiser® Lager, Corona® Extra, Guinness® Extra Stout, Heineken® Lager, Tsingtao® Lager, (Juices: a6–b3) Tropicana® Grape, Tropicana® Lemonade, Tropicana® Orange No Pulp, Campbell's® Tomato, (Liquor: b4) Disaronno® Originale Amaretto, (Milks: b5–c5) Horizon® 1% Low Fat, Horizon® 2% Reduced Fat, Horizon® chocolate, Horizon® Fat Free, Silk® Soy, Horizon® strawberry, Horizon® Whole, (Red wines: c6–d2) Chateau de Castelneau Merlot, Liberty School Syrah, Graham Beck Cabernet Sauvignon, (Sodas: d3–6) Coca Cola® Classic, Diet Coke®, Dr Pepper®, Fanta® Orange. Scale bar is 500 μm. | ||
Gabor features are represented by the Gabor vector fG. Gabor filters are a set of filters, also called Gabor wavelets, designed to describe the local texture properties of an image in various directions and scales.28 In our case, we designed Gabor filters in 4 scales and 6 directions, giving 24 filters in total. Each filter returns two values or responses. We divide each cropped image along the vertical and horizontal symmetry axis into 4 sub-images, and perform Gabor transform on each sub-image. With 24 filters, there are 48 response results for each sub-image, corresponding to a Gabor vector fG of size 192 × 1 for each image. Fig. 2d–g shows some Gabor transform results on a sub-image.The size feature vector fS, of size 1 × 1, was simply set as the total number of pixels in the cropped image.
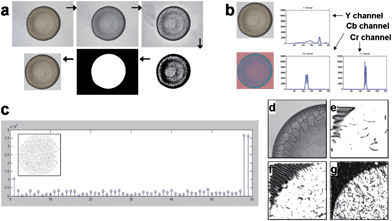 | ||
| Fig. 2 Description of the sequence of operation involved in the pattern recognition process (a) Image preprocessing by localization and cropping process: raw RGB input image (Horizon® 1% low fat milk) → converted grayscale image → enhanced contrast → converted binary image → filling hole of the inverted image → cropped image with an offset on all sides; (b) extraction of the color feature: a raw RGB input image is converted to a YCbCr image to acquire histograms of Y, Cb and Cr color channels; (c) local binary pattern (LBP) feature extraction: LBP histogram with LBP code image (inset); (d–g) Gabor wavelet feature extraction: (d) one of 4 sub-images from a grayscale image, (e) Gabor transformed image with scale 2 and degree 0, (f) scale 3 and degree 30 and (g) scale 4 and degree 60. | ||
Description of the pattern recognition algorithms
For classification purposes, the k-nearest neighbor algorithm was used. For clustering, three algorithms were compared, the k-means, average linkage and spectral clustering algorithms. These algorithms can be described as follows.k-nearest neighbor classification algorithm30,31 (k-NN)
The k-nearest neighbor algorithm (k-NN) is a supervised learning algorithm for classifying objects based on closest training examples in the feature space. A training dataset X = {(xi,yi)}ni = 1 of n labeled images is first built with each image represented by its feature vector xi ∈ Rd, and by its known integer class label yi ∈ {1,…,c}, with c the chosen number of classes. Then a test object z ∈ Rd is classified to the majority class of its k nearest neighbors in the training set to the minimum ‖z−xi‖. In the case of k = 1, an object is simply assigned to the class of its nearest neighbor in the training dataset.Feature normalization
To balance the importance of each feature used in classification, we linearly normalize each feature dimension in the training data into the interval [0, 1], and then apply the same transformation to the associated feature dimension in the test data. Specifically, let fi be the ith feature dimension of the n training data, and let fi,min = min(fi), and fi,max = max(fi). The goal is to apply a linear transformation:so that Ti(fi,min) = 0 and Ti(fi,max) = 1. Note that this can be achieved with:
For a test image x = (x1,…,xd), we then apply the transformation T(x) = (T1(x1),…,Td(xd)) before making the classification. For clustering, each feature dimension of the data is linearly normalized to interval [0, 1].
k-means clustering algorithms32
For an unlabeled dataset z1,…,zn ∈ Rd, the k-means algorithm aims to find k centers c1,…,ck ∈ Rd to minimize the following quantization loss:The integer number k is a manually set number that corresponds to the number of clusters into which the images are to be sorted. An object is then grouped to its nearest center, using the nearest neighbor algorithm. Solving this optimization problem exactly is computationally expensive. In practice, one alternates between the data partition and center update. First, k centers are randomly selected. Second, each object is grouped to its nearest center. Third, the current center in a cluster is replaced by the means of the objects in that cluster. The latter two steps are repeated until convergence.
Average linkage algorithm33
The average linkage algorithm belongs to the family of linkage clustering algorithms. It yields a cluster hierarchy over the data, in a bottom-up manner. Each object is treated as an individual cluster first. Then, the two closest clusters are merged. This procedure is repeated until some desired conditions are met. In our case, we stop the process when k clusters of the data are obtained. In average linkage, the distance between two clusters is taken as the average distance between objects across clusters, i.e.:where ni and nj denote the numbers of objects in clustersCi and Cj, respectively.
Spectral clustering algorithm34
The spectral clustering algorithm is a graph-based method. Given a dataset, a graph is built with each object as a node, and the similarity between two objects serves as the weight on the edge joining the associated nodes. Let W = (wij) be the similarity matrix of the graph, with wij capturing the similarity between nodes i and j. Typically, one takes:| wij = exp(−‖xi−xj‖2/σ), |
| di = ∑jwij, |
| Lv = λDv |
Normalized mutual information35 (NMI)
To measure the quality of the clustering process, the NMI method is applied as follows. For a clustering of the data, denoted as P1 = (C1,…,CK), we can define a discrete random variable X as the cluster-membership of a randomly selected object. Thus X can take on K values, andwhere ni is the number of objects in clusterCi. Suppose Y is the random variable associated with another partition of the same data P2 = (A1,…,AM). The joint distribution of X and Y is:
where nij is the number of objects in Ci ∩ Aj. The NMI between the partition P1 and P2 is defined as:
where I(X,Y) is the mutual information between X and Y, and H(X) and H(Y) are the entropies of X and Y, respectively. NMI is within the closed interval [0, 1], and the larger the better.
Results and discussion
Visual inspection of stains from consumable fluids
Fig. 1 shows the stains obtained from the consumable fluid drops. All stains had approximately the same size, roughly equal to the initial wetted area. The stains were highly reproducible for a given consumable fluid and distinct among fluid types. Beer stains showed no significant differences in terms of shape and color except for the Guinness® Extra Stout, which showed a browner annulus in the vicinity of the wetting line as the stout itself was darker than the other beers. Some waves or fingering were visible along the wetting line in the Tropicana® grape juice stain, while other stains from juice showed no fingering at the wetting line. Circular black spots and fibrous deposits were observed in the stains from orange and tomato juices, respectively. The stains from seven types of milks showed different levels of brown color, which seemed proportional to the nominal concentration of fat. On the other hand, crack patterns were observed on the peripheral annulus for the samples with the lowest fat concentration. Milk stains with additional ingredients like chocolate, strawberry, as well as soy milk, showed randomly distributed spots. Wine stains from Merlot and Cabernet Sauvignon showed radial wrinkles, while stains from Syrah did not. The four kinds of soda stains showed similar ring deposits, with a thick ring for the sugary sodas and a thin ring for the sugar-free diet Coke.Pattern recognition of stains from consumable fluids
We first applied a simple method, the k-nearest neighbor (k-NN) algorithm30 with k = 1 (see Methods) for the classification of the dataset of stains from consumable fluids. The Euclidean distance metric was used to measure the distances between feature vectors. In the set of the consumable fluids, shown in Fig. 1, there were 24 classes, with 20 images in each class. We used 10 images from each class as training data, and treated the remaining 10 images as test data. We tested classification accuracy based on each extracted feature vector like color distribution, LBP, Gabor wavelet and size feature and their combination, according to the image processing steps shown in Fig. 2. Despite its simplicity, the 1-NN algorithm based on the extracted features significantly improved the classification accuracy compared to random assignments, which was only 4.2% (Fig. 3a). Especially, color distribution feature played a dominant role in classification with an accuracy reaching 94%, while other features, LBP, Gabor wavelet and size features returned accuracies of 89%, 75%, and 17%, respectively. Most of the inaccuracy of the classification based on the color distribution feature aroused from beer stains as shown with the confusion matrix (see Fig. S1, ESI†). This is because the beer stains looked very similar. The classification accuracy of the beer stains based on the color distribution feature was 72% and excluding beer stains from the dataset increased the classification accuracy of consumable fluids stains to 99%.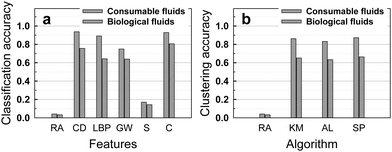 | ||
| Fig. 3 The use of (supervised) classification and (unsupervised) clustering pattern recognition algorithms identifies stains much more accurately than by random assignment: (a) Classification accuracy of the consumable and biological fluids based on the random assignment and the 1-nearest neighbor algorithm using the color distribution, local binary pattern, Gabor wavelet, size and combination features. (b) Clustering accuracy of consumable and biological fluids based on the random assignment and in the normalized mutual information (NMI) using the color distribution feature. RA: Random Assignment. CD: Color Distribution. LBP: Local Binary Pattern. GW: Gabor Wavelet. S: Size. C: Combination. KM: K-Means. AL: Average Linkage. SP: Spectral Clustering. | ||
Classification based on a combined feature vector f = [αfC, βfL, γfG, εfS], with optimal value of the weighting factors α = 1−β − γ − ε, was determined using the leave-one-out cross-validation (LOOCV)26 method described in the Methods section. Each of the weighting factors ranged between 0 and 1. For the consumable fluid data, the best weighting factors determined by the LOOCV method were α = 0.8, β = 0.1 and γ = 0.1, and ε = 0; this corresponded to a classification accuracy of 93%, which is slightly lower than the accuracy based on the color distribution feature alone (94%). Though this result appears to be counter intuitive, it is possible in practice. When a single feature is dominant in classification performance, combination of that feature with less dominant features may not improve or even degrade the accuracy. The confusion matrix for the classification accuracy of consumable fluids based on the 1-nearest neighbor algorithm using LBP, Gabor wavelet, size, and combination of features is shown in Fig. S1, ESI.†
We also applied several popular clustering algorithms to the dataset including k-means,32 average linkage,33 and spectral clustering34 (described in the Methods section). Clustering is the process of grouping data into clusters, such that objects within a cluster are similar to each other while those across clusters are dissimilar, under certain criteria. In order to measure the quality of the clustering performance, we adopt the Normalized Mutual Information (NMI)35 by measuring the normalized mutual information between the clustering result and the ground-truth clusters (see Methods). The maximum clustering accuracy of 87% for the consumable fluid dataset in NMI was achieved when the color distribution feature was used as shown in Fig. 3b.
Visual inspection of stains from biological fluids
Another collection of stain images was prepared using biological fluids (Fig. 4) such as phosphate buffer (K2HPO4/KH2PO4) at different volume ratio, phosphate solutions (K2HPO4) added of different volumes of citric acid to control pH, and KOH solutions. To detect the effects of specific molecular interactions between the solution and the solid substrate, two versions of each fluid were prepared (one including biotin, and the other not), and two versions of the glass slides were prepared (one coated with streptavidin and the other not). The biotin-streptavidin system was chosen because it is known to be the strongest non-covalent interaction between a protein and its cofactor binding constant of the system, i.e. KD = 4 × 10−14 M36 or, equivalently, a force of 160 pN as measured by atomic force microscopy.37 This system also has a widespread use in biotechnology,38 in particular in high affinity sensitive immunoenzymatic assays (e.g. ELISA).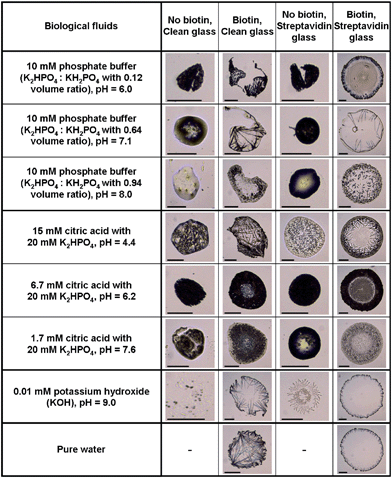 | ||
| Fig. 4 Stains of biological fluids show complex patterns that can be used for identifying the fluid and substrate chemistry. The fluid composition is given in the first column. The first row states whether the fluid contains biotin or not, and whether the glass slide used has been simply cleaned with Piranha solution or coated with streptavidin. The scale bar is equal to 200 μm. | ||
All the prepared biological fluids deposited on the clean glass and streptavidin-coated glass slides formed unique stains as shown in Fig. 4, except the pure water droplet deposited on a clean glass slide (which is not shown because it did not leave a visible stain and attests of the purity of the aqueous solutions made). The variation in diameter of the biological stains was on the order of one order of magnitude, much larger than for the consumable stains. When drops of 10 mM phosphate buffer with different volume ratio were deposited on the clean and streptavidin-coated glass slides, a small-diameter bump was formed, probably because of Marangoni convection coupled with receding of the initial wetting line.23 Visual inspection revealed the following about the effect of pH: the most acid solutions (15 mM citric acid solution) left crystallized patterns in the bump on the clean glass slide and scattered granular patterns on the streptavidin coated glass slide, while more basic solutions (6.7 mM and 1.7 mM of citric acid) formed more homogeneous bumps on both glass slides. Interestingly, the KOH solution deposited on the streptavidin-coated glass slide showed circular snowflake stains whereas it formed random spots on the clean glass slide. Adding 1.32 mM biotin to each solution drastically changed the stain pattern, as shown by comparing the first with the second column in Fig. 4 for the clean glass surface and the third with the fourth column for the streptavidin-coated glass case. The presence of biotin in the phosphate buffer with 15 mM citric acid produced needle patterns in the stains when deposited on the clean glass slide, whereas it formed globular patterns when biotin was not in solution. Addition of biotin to KOH and pure water deposited on the clean glass slide produced thin needles pointing inward from the periphery. Stains from all the solutions added with biotin maintained circular shapes after the drying process, possibly due to its strong non-covalent interaction between biotin in solution and streptavidin coated on the glass slide. However, different patterns were observed at the interior of the stains depending on the solution used. Altering the volume ratio of the phosphate buffers resulted in stains with short needles at the wetting line and multiple concentric lines inside the wetting line, coarse long needles pointing inward at the periphery without inside concentric lines and scattered granular pattern, as the volume ratio increased. The 10 mM citric acid in phosphate solution with biotin showed thorny crown patterns when deposited on the streptavidin coated glass slide. Stains from 6.7 mM and 1.5 mM citric acid in phosphate solution with biotin on the streptavidin glass slide formed more apparent annular ring patterns compare to when deposited on the clean glass slide. Pure water and KOH drops added with biotin showed almost identical stains when deposited on the streptavidin coated glass slide, i.e. shorter needles around the periphery than when deposited on the clean glass slide.
Pattern recognition of the images from biological fluids
The dataset of biological fluids includes 30 classes with different fluid composition and substrate chemistry. 20 images were taken per class, with 10 images per class used as training data and the remaining images used to test the pattern recognition algorithms. The accuracy of the classification process is shown in Fig. 3a. The best accuracy of 81% is obtained by the combination of the four features (color, LBP, Gabor and size), and compares favorably with an accuracy of 3.3% obtained by random assignment. As with the dataset of consumable fluids, the color distribution was the most discriminative single feature, followed by the LBP, Gabor and size feature. Contrary to the dataset of consumable fluids, the combination of four features provided higher accuracy than the single feature of color distribution, probably because the features observed in the biological fluids were richer than the ones observed in the consumable fluids, see Fig. S2, ESI.† The classification accuracy with the biological fluids was not as high as the accuracy with the consumable fluids.Fig. 3b shows the clustering accuracy, using three different clustering algorithms. The spectral clustering algorithm delivered the best result, with 66% accuracy for 30 classes.
Fig. 5 describes the performance of classification algorithms to determine the presence or absence of biotin and streptavidin respectively in the liquid and on the glass (4 classes), the salt composition (3 classes), or the pH of the solution (3 classes). For each of the three tasks, pattern recognition algorithms using combined features returned a classification accuracy larger than 90%. This is a remarkable result since the influence on the stain image of pH, biotin/streptavidin, and citric acid is difficult to determine by visual inspection.
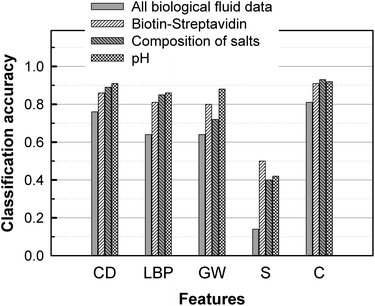 | ||
| Fig. 5 Accuracy of pattern recognition algorithms for detection of biotin and streptavidin, salt composition, and pH, based on single features (first four rows) or a combination of all features. RA: Random Assignment. CD: Color Distribution. LBP: Local Binary Pattern. GW: Gabor Wavelet. S: Size. C: Combination. | ||
Conclusions
Biological and consumable fluids were classified and clustered by pattern recognition techniques based on the descriptive features (color distribution, local binary pattern, Gabor wavelet, and size) extracted from photographic images of the stains. For both datasets, the color distribution was the most discriminative single feature. The nearest neighbor classification based on the combined feature achieved the highest classification and clustering accuracy for biological fluids. However, for consumable fluids, the color distribution feature alone achieved the highest accuracy. Results with the dataset of stains from consumable fluids showed a slightly higher accuracy than that from biological fluids. This is probably due to the large variations of composition of the biological fluids considered. The algorithms were also remarkably accurate at determining the presence or absence of biotin and streptavidin respectively in the liquid and on the glass, the salt composition, or the pH of the solution. The pattern recognition scheme developed in this work showed feasibility of pattern recognition in recognizing specific fluids from the raw stain images of the fluids. This work is the first example of computer-based classification and clustering of stains from consumable and biological fluids using pattern recognition algorithms. The application of this methodology for clinical diagnostics, such as the classification of pleural effusions for malignancy, congestive heart failure or lung infection, has the potential to enable rapid screening at the point-of-care. The interest of the method lies in the possibility of investigating other protein systems than avidin/biotin in order to: 1) quickly determine protein content of clinical samples such as pleural effusions or cerebrospinal fluid for early diagnosis, and 2) investigate specific interactions between the fluid and biomarkers patterned on the surface. Future improvements of the method include increasing the throughput by involving the use of a micro-arrayer to form the droplets.Acknowledgements
NK, DA, ZL and SFC acknowledge support from NSF award #1034349. CH and FZ acknowledge support from the iBis Foundation of Arizona.Notes and references
-
D. Maltoni, Handbook of fingerprint recognition. Springer-Verlag, New York, 2003 Search PubMed
.
- W. Zhao,
et al., Face recognition: a literature survey, ACM Comput. Surv., 2003, 35, 399–458 CrossRef
.
- L. R. Rabiner, A tutorial on hidden Markov models and selected applications in speech recognition, Proc. IEEE, 1989, 77, 257–286 CrossRef
.
- R. Plamondon and S. N. Srihari, Online and offline handwriting recognition: a comprehensive survey, IEEE Trans. Pattern Anal. Mach. Intell., 2000, 22, 63–84 CrossRef
.
- J. W. Gardner and P. N. Bartlett, A brief history of electronic noses, Sens. Actuators, B, 1994, 18, 210–211 CrossRef
.
- P. Ciosek and W. Wróblewski, The analysis of sensor array data with various pattern recognition techniques, Sens. Actuators, B, 2006, 114, 85–93 CrossRef
.
- P. Ciosek, Z. Brzózka and W. Wróblewski, Classification of beverages using a reduced sensor array, Sens. Actuators, B, 2004, 103, 76–83 CrossRef
.
- Q. Chen, J. Zhao and S. Vittayapadung, Identification of the green tea grade level using electronic tongue and pattern recognition, Food Res. Int., 2008, 41, 500–504 CrossRef CAS
.
- C. Krantz-Rülcker, M. Stenberg, F. Winquist and I. Lundström, Electronic tongues for environmental monitoring based on sensor arrays and pattern recognition: a review, Anal. Chim. Acta, 2001, 426, 217–226 CrossRef
.
- L. A. Berrueta, R. M. Alonso-Salces and K. Héberger, Supervised pattern recognition in food analysis, J. Chromatogr., A, 2007, 1158, 196–214 CrossRef CAS
.
- R. Blossey and A. Bosio, Contact line deposits on cDNA microarrays: a “twin-spot effect”, Langmuir, 2002, 18, 2952–2954 CrossRef CAS
.
- G. T. Carroll, D. Wang, N. J. Turro and J. T. Koberstein, Photochemical micropatterning of carbohydrates on a surface, Langmuir, 2006, 22, 2899–2905 CrossRef CAS
.
- V. Dugas, J. Broutin and E. Souteyrand, Droplet evaporation study applied to DNA chip manufacturing, Langmuir, 2005, 21, 9130–9136 CrossRef CAS
.
- I. I. Smalyukh, O. V. Zribi, J. C. Butler, O. D. Lavrentovich and G. C. L. Wong, Structure and dynamics of liquid crystalline pattern formation in drying droplets of DNA, Phys. Rev. Lett., 2006, 96, 177801 CrossRef
.
- D. Wang, S. Liu, B. J. Trummer, C. Deng and A. Wang, Carbohydrate microarrays for the recognition of cross-reactive molecular markers of microbes and host cells, Nat. Biotechnol., 2002, 20, 275–281 CrossRef CAS
.
-
R. G. Larson, M. A. Lopez, D. W. Lim and J. Lahann, Complex protein patterns in drying droplets, Materials Research Society Spring Meeting, San Francisco, CA, April 5–9, 2010 Search PubMed
.
- T. Cuk, S. M. Troian, C. M. Hong and S. Wagner, Using convective flow splitting for the direct printing of fine copper lines, Appl. Phys. Lett., 2000, 77, 2063–2065 CrossRef CAS
.
- M. Maillard, L. Motte and M. P. Pileni, Rings and hexagons made of nanocrystals, Adv. Mater., 2001, 13, 200–204 CrossRef CAS
.
- T. Ondarçuhu and C. Joachim, Drawing a single nanofibre over hundreds of microns, Europhys. Lett., 1998, 42, 215–220 CrossRef
.
- R. Bhardwaj, X. Fang and D. Attinger, Pattern formation during the evaporation of a colloidal nanoliter drop: a numerical and experimental study, New J. Phys., 2009, 11, 075020 CrossRef
.
- R. Bhardwaj, X. Fang, P. Somasundaran and D. Attinger, Self-assembly of colloidal particles from evaporating droplets: role of DLVO interactions and proposition of a phase diagram, Langmuir, 2010, 26, 7833–7842 CrossRef CAS
.
- R. D. Deegan,
et al. Capillary flow as the cause of ring stains from dried liquid drops, Nature, 1997, 389, 827–829 CrossRef CAS
.
- H. Hu and R. G. Larson, Marangoni effect reverses coffee-ring depositions, J. Phys. Chem. B, 2006, 110, 7090–7094 CrossRef CAS
.
- G. Chen and G. J. Mohamed, Complex protein patterns formation via salt-induced self-assembly and droplet evaporation, Eur. Phys. J. E, 2010, 33, 19–26 CrossRef CAS
.
- A. K. Jain, R. P. W. Duin and J. Mao, Statistical pattern recognition: a review, IEEE Trans. Pattern Anal. Mach. Intell., 2000, 22, 4–37.
-
S. Sergyan, Color histogram features based image classification in content-based image retrieval systems, The Sixth International Symposium on Applied Machine Intelligence and Informatics, 2008, 221–224
.
- T. Ojala, M. Pietikäinen and D. Harwood, A comparative study of texture measures with classification based on featured distributions, Pattern Recognition., 1996, 29, 51–59 CrossRef
.
- B. S. Manjunath and W. Y. Ma, Texture features for browsing and retrieval of image data, IEEE Trans. Pattern Anal. Mach. Intell., 1996, 18, 837–842 CrossRef
.
- The datasets used in this work are available for download, distributed for non-commercial research purpose only, at: mailto:http://www.ee.columbia.edu/dvmm/staindata Please cite this work in publications of any work that uses the datasets.
- T. M. Cover and P. E. Hart, Nearest neighbor pattern classification, IEEE Trans. Inf. Theory, 1967, 13, 21–27 CrossRef
.
- M. Stone, Cross-validatory choice and assessment of statistical predictions, Journal of the Royal Statistical Society. Series B (Methodological), 1974, 36, 111–147 Search PubMed
.
-
J. B. MacQueen, Some methods for classification and analysis of multivariate observations, The fifth Berkeley symposium on mathematical statistics and probability, 1967 Search PubMed
.
- A. K. Jain, M. N. Murty and P. J. Flynn, Data clustering: a review, ACM Comput. Surv., 1999, 31, 264–323 CrossRef
.
- J. Shi and J. Malik, Normalized cuts and image segmentation, IEEE Trans. Pattern Anal. Mach. Intell., 2000, 22, 888–905 CrossRef
.
- A. Strehl, J. Ghosh and C. Cardie, Cluster ensembles - a knowledge reuse framework for combining multiple partitions, Journal of Machine Learning Research, 2003, 3, 583–617 Search PubMed
.
- A. Holmberg,
et al., The biotin-streptavidin interaction can be reversibly broken using water at elevated temperatures, Electrophoresis, 2005, 26, 501–510 CrossRef CAS
.
- V. Moy, E. Florin and H. Gaub, Intermolecular forces and energies between ligands and receptors, Science, 1994, 266, 257–259 CAS
.
- E. Diamandis and T. Christopoulos, The biotin-(strept)avidin system: principles and applications in biotechnology, Clin Chem, 1991, 37, 625–636 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c1ay05338h |
| This journal is © The Royal Society of Chemistry 2012 |