A stereoselectively deuterated supramolecular motif to probe the role of solvent during self-assembly processes

Abstract

Small changes in the alkane solvent structure in combination with temperature effects lead to four different conformations of stereoselectively deuterated benzene-1,3,5-tricarboxamides in the aggregated state, affecting the expression of the supramolecular chirality and highlighting the role of the solvent structure in self-assembly processes.

---

The spontaneous self-assembly of molecules into well-defined aggregates is the result of a subtle interplay of non-covalent interactions between molecules, and solvophobic effects between the solvent and both the individual molecules and the aggregates.¹ This is often rationalised in terms of preferential solvation by specific interactions between the solvent and the aggregates, but in some cases only London dispersion forces can be assigned.^1j Intriguingly, variations in solvent polarity can induce a change in the preferred helicity in some helical polymers.² Moreover, the application of chiral, non-racemic solvents was found to bias one helical sense in the self-assembly processes of achiral small molecules, conjugated oligomers and polymers, suggesting that also tiny differences in the solvent structure suffice to induce a helical bias.³ In the latter case, the role of the molecular structure of the solvent during self-assembly is still poorly understood.

We studied in detail the self-assembly of benzene-1,3,5-tricarboxamides (BTAs) into helical, columnar, one-dimensional supramolecular polymers in dilute alkane solutions.⁴ In the absence of chiral information, BTAs form right-handed (P) and left-handed (M) helical supramolecular polymers in equal amounts. One stereogenic methyl group on the alkyl side chain suffices to fully bias one helical sense. Recent DFT calculations revealed that differences in the dihedral angles θ of the amide with respect to the central benzene ring lead to differently shaped Cotton effects (Fig. 1A).^4c A single Cotton effect is indicative for a dihedral angle θ ≈ 45° (conformation type 1, H1) while a double Cotton effect is a representative for a dihedral angle θ ≈ 35° (conformation type 2, H2) (Fig. 1B). In addition, the molecular structure of the alkane solvent influenced the preference of H1 over H2. In order to unravel the remarkable sensitivity of the molecular structure of the solvent on the self-assembly of small molecules, we apply BTAs as a model system. More specifically, we use a BTA that owes its chirality due to the introduction of stereoselective H/D isotopes into the α-position of the alkyl side chains (Fig. 1A). The extent to which the isotope substituent influences the supramolecular chirality proved to be sensitive to temperature and solvent.⁵ By now studying this self-assembly behaviour systematically as a function of solvent, temperature and concentration, we show that (S,S,S)-D-BTA is a highly sensitive probe to investigate the effect of the molecular structure of the alkane solvent on the self-assembly of conformationally flexible supramolecular polymers.

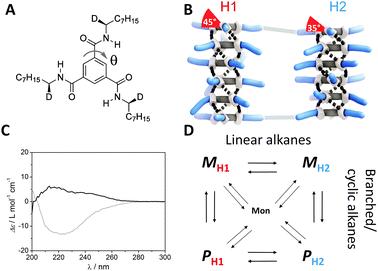Fig. 1 (A) Structure of (S,S,S)-D-BTA; θ is the dihedral angle of the amide with respect to the central benzene ring. (B) Schematic representation of BTAs present in the two conformers, H1 and H2, both showing M helicity. (C) CD spectra of (S,S,S)-D-BTA in heptane (grey line) and MCH (black line) at T = 20 °C, c = 50 μM. (D) Four possible states of the supramolecular polymers of (S,S,S)-D-BTA in equilibrium with the monomer in alkane (linear, cyclic or branched) solvents.

The self-assembly behaviour of (S,S,S)-D-BTA in heptane and methylcyclohexane (MCH) (c = 50 μM) was investigated at 20 °C by circular dichroism (CD) and ultraviolet (UV) spectroscopy. While the UV spectra in both solvents are similar (Fig. S1, ESI‡), the CD spectra differ in sign, intensity, and shape (Fig. 1C). The CD spectrum in MCH shows a small, positive, double Cotton effect with λ_max = 216 nm (Δε ≈ 6 M⁻¹ cm⁻¹) and a shoulder at 242 nm, while a larger, negative, single Cotton effect with λ_max = 223 nm (Δε ≈ −13 M⁻¹ cm⁻¹) is observed in heptane. Whereas the sign of the Cotton effect is indicative for the type of the excess helical sense, P or M, the intensity of the Cotton effect determines the excess helical sense quantitatively. In chiral alkyl-substituted BTAs the characteristic absolute molar ellipticity |Δε| is around 40 M⁻¹ cm⁻¹ in various alkane solvents.⁴ This value is indicative for the formation of one type of helical supramolecular polymer, i.e. the diastereomeric excess (d.e. = ([M] − [P])/([M] + [P]) × 100) is 100%. Thus, in MCH the preferred helical sense for (S,S,S)-D-BTA is P (d.e. = −15%) whereas in heptane, M is the pronounced helical sense (d.e. = 33%). The shape of the CD effect reflects the conformation of the amide bonds of the monomer within the supramolecular polymer.^4c As a result, the single Cotton effect in heptane indicates that the majority of the (S,S,S)-D-BTA-based supramolecular polymers demonstrate a H1 conformation, whereas the double Cotton effect in MCH is indicative for the H2 conformation. We propose that there are four possible conformational states of (S,S,S)-D-BTA-based supramolecular polymers, P_H1, P_H2, M_H1, M_H2 and they all are in equilibrium (Fig. 1D). At room temperature, the equilibrium favors M_H1 in heptane while in MCH, P_H2 is the most dominant type of supramolecular polymer.

To show the interchange of the four conformers in the (S,S,S)-D-BTA self-assembly, temperature-dependent UV and CD spectroscopy was performed in MCH and heptane from 363 to 263 K. The temperature-dependent UV curves of (S,S,S)-D-BTA in MCH and heptane (probed at λ = 223 nm, c = 50 μM) are similar and typical for a cooperative supramolecular polymerization process (Fig. S2, ESI‡). Temperature-dependent UV measurements directly relate to the degree of aggregation in a self-assembly process allowing determination of the thermodynamic parameters in each solvent (Fig. S3 and Table S1, ESI‡).^1j,4a The values for the temperature of elongation, T_e, the enthalpy of elongation, h_e, and the association constant for activation, K_a, determined by fitting the data with a nucleation-elongation model^4a differ for both solvents. The T_e in MCH (343.4 K) is lower than that in heptane (355.6 K), reflecting the better solubility of the monomers in MCH. The dimensionless activation constant K_a—a measure for the cooperativity—is smaller in heptane (1.3 ± 0.3 × 10⁻⁴) than in MCH (6.8 ± 0.3 × 10⁻⁴) reflecting a higher cooperativity of the aggregation process in heptane. The h_e, a measure for the aggregate stability, is similar and around −65 kJ mol⁻¹. In contrast, the temperature-dependent CD measurements of (S,S,S)-D-BTA in MCH and heptane differ completely (Fig. 2A). In MCH, the positive sign of the molar ellipticity Δε increases, then decreases and becomes negative at 267 K upon cooling. This switch in sign (from +5.0 M⁻¹ cm⁻¹ to −1.5 M⁻¹ cm⁻¹) indicates a change in excess helical sense from P to M. In this temperature regime, the CD spectra always show double Cotton effects, indicating that the H2 conformer is dominant (Fig. S4, ESI‡). In heptane, the Cotton effect always has a negative value suggesting that the M type helical sense is in excess at each temperature. However, upon cooling the Cotton effect switches from single to double around 297 K, suggesting a conformational change from H1 to H2 (Fig. S4 and S5, ESI‡). The latter implies that the four possible conformational states of (S,S,S)-D-BTA-based supramolecular polymers are in thermodynamic equilibrium. The position of the equilibrium depends on the molecular structure of the alkane solvent and the temperature.

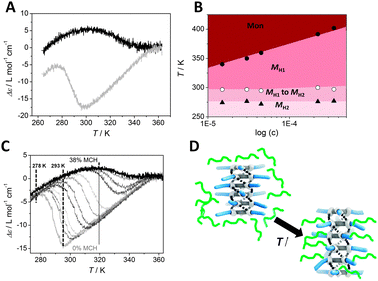Fig. 2 (A) Molar ellipticity Δε as a function of temperature for (S,S,S)-D-BTA in MCH (black line) and in heptane (grey line) (c = 50 μM, λ = 223 nm, cooling rate = 1 K min⁻¹). (B) Pseudo-phase diagram derived from Fig. S6, ESI.‡ (C) CD cooling curves of D-BTA in heptane (grey line) to heptane/MCH 62/38% v/v (black line) with MCH added in portions of ∼3% v/v (c = 50 μM, cooling rate = 1 K min⁻¹, λ = 223 nm). (D) Schematic representation of the intercalation of heptane (depicted in green) between BTAs of the supramolecular aggregate. As a result, the conformation changes from H2 to H1.

As can be seen in Fig. 2A, the transition from H1 to H2 at 293 K in heptane is quite sharp. If the transition between two states of a supramolecular polymer is cooperative, theory predicts a weakly concentration-dependent transition.⁶ At equilibrium, assuming that the average number of monomers in each type of aggregate is large, the chemical potentials of the monomers associated with the two aggregation states are dominated by their respective binding energies. The reason that the concentration dependence drops out is because, on a per monomer basis, it is proportional to the reciprocal aggregation number.^6,7a Thus, we measured concentration-dependent CD cooling curves of (S,S,S)-D-BTA in heptane between 15 μM and 350 μM (Fig. S6, ESI‡). From these data, we derived a pseudo-phase diagram by using the temperature of elongation (T_e) at which monomers start forming M_H1 type supramolecular polymers in excess, the temperature of transition at which M_H1 switches to M_H2 and the temperature at which M_H2 becomes the dominant conformation (Fig. 2B). The transition between M_H1 and M_H2 starting at 297 K is indeed almost concentration independent as is the transition at which M_H2 becomes the dominant conformation (=279 K). This result is analogous to that experimentally found for bisurea systems in which a concentration-independent, cooperative filament to tube transition occurs and for water soluble bipyridine based discotics in which a non-helical to helical transition was observed.^7,8 In all cases, the experimental pseudo-phase diagrams derived from concentration-dependent measurements are in excellent agreement with the theoretically predicted phase diagrams for a cooperative transition between two long, supramolecular polymers with two different conformations.⁶

Next, we evaluated if there is a dominance of one of the solvents, heptane or MCH, in a mixture. For this purpose, we mixed solutions of (S,S,S)-D-BTA in MCH and heptane with identical concentrations (c = 50 μM). The UV and CD spectra of (S,S,S)-D-BTA in solutions ranging from pure heptane to a mixture of heptane/MCH 62/38% v/v were measured as a function of temperature at λ = 223 nm. The shapes of the temperature-dependent UV cooling curves are similar for each mixture indicating that the aggregation behavior of (S,S,S)-D-BTA is similar in the mixed solvents (Fig. S7, ESI‡). The CD cooling curves, in contrast, are highly sensitive to the amount of MCH added (Fig. 2C, Fig. S8, ESI‡): the |Δε| decreases upon increasing the amount of MCH and the temperature at which the transition between the conformers H1 and H2 occurs, increases from 296 K to 340 K. Interestingly, the pronounced effect of MCH on the intensity of the Cotton effect observed at 293 K is almost absent at 278 K (Fig. 2C, Fig. S9, ESI‡), indicating that MCH only has a pronounced effect on the intensity of the Cotton effect when the H1 conformer dominates, i.e. when the amide dihedral angle θ is around 45°. We attribute this behavior to the ability of the linear heptane to absorb preferentially or intercalate between the alkyl residues of the BTA molecules within the stack, as schematically depicted in Fig. 2D. Upon increasing the temperature in pure heptane or increasing the heptane concentration in the heptane–MCH mixtures, heptane intercalation between BTAs results in an increase of the interdisc distance and a concomitant increase in the dihedral angle θ from 35° to around 45° (Fig. 1B). As a result, H1 becomes the preferred conformer. Upon heating, the contribution of the heptane intercalation to the association enthalpy between the BTA molecules and the solvent is positive rather than negative. Since the free energy of this process must be negative, this observation implies that solvent intercalation into the stack is entropy driven, e.g., by enhanced conformational freedom of these side chains due to a larger separation between BTAs in the stacks and mixing with the side chains. The absorption of the heptane in the space between the side chains increases the configurational or mixing entropy of the mixture of side chains and heptane most when half of the spaces are occupied, in analogy with the (ideal) mixing of binary fluids. The higher bias caused by heptane is connected to an increased dihedral angle θ ≈ 45° suggesting that a linear solvent effectively helps in biasing one helical sense over the other. In fact, a clear preference for the M helical sense is also observed in other linear alkane solvents at room temperature such as hexane, octane, nonane, decane and dodecane (Fig. S10, ESI‡). In contrast, the CD spectra of (S,S,S)-D-BTA in branched and cyclic solvents such as isooctane, cyclohexane and decaline show no or only a very small Cotton effect at room temperature (Fig. S11, ESI‡). These observations support that linear alkanes actively participate in the self-assembled structures and increase the bias for one helicity in D-BTA aggregates. Thus, weak London dispersion forces present between the alkane solvent and BTA alkyl chains assist in expressing a preferred helicity. In the absence of this preferential interaction (as is the case with branched/cyclic solvents), the ability of the deuterium to favor one helicity is reduced. Similar effects have been observed in helical polyisocyanates although in this case the dielectric constants of the solvents in the mixture were quite different.^2a

In conclusion, the effect of the molecular structure of the solvent during self-assembly processes is probed sensitively by (S,S,S)-D-BTA molecules. The results presented here provide additional evidence for the existence of a bound solvent shell around or even partially incorporated into structures formed by self-assembling molecules. While in protein folding the role of water is widely recognized to play a dominant role, solvophobic effects may be equally important for self-assembling systems in organic media. Gathering precise knowledge on these additional weak interactions during self-assembly is difficult yet is important especially when applications in the field of catalysis or organogelators are envisaged.

Notes and references

1. (a) Y. Pinault, B. Isare and L. Bouteiller, ChemPhysChem, 2006, 7, 816; (b) W. Edwards, C. A. Lagadec and D. K. Smith, Soft Matter, 2011, 7, 110; (c) J. van Esch, F. Schoonbeek, M. de Loos, H. Kooijman, A. L. Spek, R. M. Kellogg and B. L. Feringa, Chem.–Eur. J., 1999, 5, 937; (d) M. George, G. Tan, V. T. John and R. G. Weiss, Chem.–Eur. J., 2005, 11, 3243; (e) Y. Jeong, K. Hanabusa, H. Masunaga, I. Akiba, K. Miyoshi, S. Sakurai and K. Sakurai, Langmuir, 2005, 21, 586; (f) V. V. Borovkov, G. A. Hembury and Y. Inoue, Angew. Chem., Int. Ed., 2003, 42, 5310; (g) M. Hutin and J. Nitschke, Chem. Commun., 2006, 1724; (h) K. Sakajiri, T. Sugisaki, K. Moriya and S. Kutsumizu, Org. Biomol. Chem., 2009, 7, 3757; (i) A. L. Hofacker and J. R. Parquette, Angew. Chem., Int. Ed., 2005, 44, 1053; (j) P. Jonkheijm, P. van der Schoot, A. P. H. J. Schenning and E. W. Meijer, Science, 2006, 313, 80.
2. (a) M. M. Green, C. A. Khatri and N. Peterson, J. Am. Chem. Soc., 1993, 115, 4941; (b) T. Yamada, Y. Nagaata and M. Suginome, Chem. Commun., 2010, 46, 4914.
3. (a) A. R. A. Palmans, J. A. J. M. Vekemans, E. E. Havinga and E. W. Meijer, Angew. Chem., Int. Ed. Engl., 1997, 36, 2648; (b) B. Isare, M. Linares, L. Zargarian, S. Fermandjian, M. Miura, S. Motohashi, N. Vanthuyne, R. Lazzaroni and L. Bouteiller, Chem.–Eur. J., 2010, 16, 173; (c) S. J. George, Z. Tomovic, A. P. H. J. Schenning and E. W. Meijer, Chem. Commun., 2011, 47, 3451; (d) S. J. George, Z. Tomovic, M. M. J. Smulders, T. F. A. de Greef, P. Leclere, E. W. Meijer and A. P. H. J. Schenning, Angew. Chem., Int. Ed., 2007, 46, 8206; (e) H. von Berlepsch, S. Kirstein and C. Bottcher, J. Phys. Chem. B, 2003, 107, 9646; (f) M. M. Green, N. C. Peterson, T. Sato, A. Teramoto, R. Cook and S. Lifson, Science, 1995, 268, 1860; (g) Y. Nakano, Y. Liu and M. Fujiki, Polym. Chem., 2010, 1, 460.
4. (a) M. M. J. Smulders, A. P. H. J. Schenning and E. W. Meijer, J. Am. Chem. Soc., 2008, 130, 606; (b) P. J. M. Stals, M. M. J. Smulders, R. Martin-Rapun, A. R. A. Palmans and E. W. Meijer, Chem.–Eur. J., 2009, 15, 2071; (c) Y. Nakano, T. Hirose, P. J. M. Stals, E. W. Meijer and A. R. A. Palmans, Chem. Sci., 2012, 3, 148; (d) M. M. J. Smulders, T. Buffeteau, D. Cavagnat, M. Wolffs, A. P. H. J. Schenning and E. W. Meijer, Chirality, 2008, 20, 1016.
5. S. Cantekin, D. W. R. Balkenende, M. M. J. Smulders, A. R. A. Palmans and E. W. Meijer, Nat. Chem., 2010, 3, 42.
6. (a) J. van Gestel, P. van der Schoot and M. A. J. Michels, J. Phys. Chem. B, 2001, 105, 10691; (b) J. van Gestel, P. van der Schoot and M. A. J. Michels, Langmuir, 2003, 19, 1375.
7. (a) M. Roman, C. Cannizzo, T. Pinault, B. Isare, B. Andrioletti, P. van der Schoot and L. Bouteiller, J. Am. Chem. Soc., 2010, 132, 16818; (b) M. Bellot and L. Bouteiller, Langmuir, 2008, 24, 14176.
8. P. van der Schoot, M. A. J. Michels, L. Brunsveld, R. P. Sijbesma and A. Ramzi, Langmuir, 2000, 16, 10076.

---

Footnotes

† This article is part of the ChemComm 'Chirality' web themed issue.

‡ Electronic supplementary information (ESI) available: Experimental details, characterization by UV and CD spectroscopy. See DOI: 10.1039/c2cc17284d

---