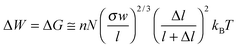Great expectations: can artificial molecular machines deliver on their promise?†
Ali
Coskun
ab,
Michal
Banaszak
c,
R. Dean
Astumian
d,
J. Fraser
Stoddart
*ab and
Bartosz A.
Grzybowski
*ae
aDepartment of Chemistry, Northwestern University, 2145 Sheridan Road, Evanston, Illinois 60208-3113, USA. E-mail: stoddart@northwestern.edu; Fax: +1-847-491-1009; Tel: +1-847-491-3793
bNanoCentury KAIST Institute and Graduate School of EEWS (WCU), Korean Advanced Institute of Science and Technology (KAIST), 373-1 Guseong Dong, Yuseong Gu, Daejeon 305-701, (Republic of Korea)
cFaculty of Physics, Adam Mickiewicz University, Poznan, Poland
dDepartment of Physics, University of Maine, Orono, ME 04469, USA
eDepartment of Chemical and Biological Engineering, Northwestern University, 2145 Sheridan Road, Evanston, Illinois 60208-3113, USA. E-mail: grzybor@northwestern.edu; Fax: +1-847-491-3728; Tel: +1-847-491-3024
First published on 25th November 2011
Abstract
The development and fabrication of mechanical devices powered by artificial molecular machines is one of the contemporary goals of nanoscience. Before this goal can be realized, however, we must learn how to control the coupling/uncoupling to the environment of individual switchable molecules, and also how to integrate these bistable molecules into organized, hierarchical assemblies that can perform significant work on their immediate environment at nano-, micro- and macroscopic levels. In this tutorial review, we seek to draw an all-important distinction between artificial molecular switches which are now ten a penny—or a dime a dozen—in the chemical literature and artificial molecular machines which are few and far between despite the ubiquitous presence of their naturally occurring counterparts in living systems. At the single molecule level, a prevailing perspective as to how machine-like characteristics may be achieved focuses on harnessing, rather than competing with, the ineluctable effects of thermal noise. At the macroscopic level, one of the major challenges inherent to the construction of machine-like assemblies lies in our ability to control the spatial ordering of switchable molecules—e.g., into linear chains and then into muscle-like bundles—and to influence the cross-talk between their switching kinetics. In this regard, situations where all the bistable molecules switch synchronously appear desirable for maximizing mechanical power generated. On the other hand, when the bistable molecules switch “out of phase,” the assemblies could develop intricate spatial or spatiotemporal patterns. Assembling and controlling synergistically artificial molecular machines housed in highly interactive and robust architectural domains heralds a game-changer for chemical synthesis and a defining moment for nanofabrication.
 Ali Coskun | Ali Coskun was born in Isparta, Turkey, in 1979. He received all (BSc, MSc, PhD) of his degrees in Chemistry from the Middle East Technical University, Turkey, while carrying out his research activities under the supervision of Professor Engin U. Akkaya. During his graduate studies, he developed supramolecular ion sensing systems and investigated their application in the area of molecular logic gates. Presently, he is a postdoctoral fellow in the laboratory of J. Fraser Stoddart at Northwestern University. His research interests include dynamic metal–organic frameworks, artificial molecular machines, organic radicals and molecular electronic devices based on switchable mechanically interlocked structures. |
 Michal Banaszak | Michał Banaszak graduated in 1985 from Adam Mickiewicz University in Poznan, Poland. He received his PhD degree in Physics in 1991 from Memorial University in St. John's, Canada. From 1992 to 1995 he worked as postdoctoral fellow in Exxon Research & Engineering Co. in Annandale, New Jersey, USA, and from 1995 to 1997 in the Chemistry Department of UMIST in Manchester, UK. In 1997 he joined the Adam Mickiewicz University, obtaining the DSc degree (habilitation) in 2004 in Physics. His main interest is in developing new models and theories for nanoscale self-assembly of various copolymer systems. |
 R. Dean Astumian | Dean Astumian received all of his degrees (BS, MS, and PhD) from the University of Texas at Arlington. After a post-doc at NIH and four years on the staff at NIST he joined the faculty at the University of Chicago where he spent the next nine years. He moved to his current position, professor of Physics at the University of Maine in 2001. He has pioneered the theoretical understanding of how noise can be put to constructive uses in molecular machines, research for which he was elected fellow of the American Physical Society (APS) and for which he received an Alexander von Humboldt research award. |
 J. Fraser Stoddart | Sir Fraser Stoddart received all (BSc, PhD, DSc) his degrees from the University of Edinburgh. His academic career can be traced from Queen’s University (Canada) to the Universities of Sheffield (1970–90) and Birmingham (1990–97) with a sojourn at the ICI Corporate Laboratory from 1978 to 1981, and then across the Pond to UCLA in 1997. Since 2008, he has held a Board of Trustees Professorship in the Department of Chemistry at Northwestern University. His research has opened up a new materials world of mechanically interlocked molecules and, in doing so, has produced a blueprint for the subsequent growth of molecular nanotechnology. |
 Bartosz A. Grzybowski | Bartosz Grzybowski graduated summa cum laude and Honoris in Chimia from Yale University in 1995. In 2000, he obtained his PhD in Physical Chemistry from Harvard University (with G. M. Whitesides). In 2003 he joined the faculty of Northwestern University where he is now Burgess Professor of Physical Chemistry and Chemical Systems Engineering. Grzybowski pioneered research on dynamic self-assembly. His other scientific interests include chemistries in non-equilibrium/dynamic systems, complex chemical networks, nanostructured materials, and nanobiology. |
Introduction
For a quarter century the vision of switchable molecules acting as nanomachines has inspired chemists,1–7 physicists,8–10 and nanoengineers11,12 alike. Despite the remarkable progress that has been made in the synthesis of ever more complex molecular switches4,13 the aim of harnessing useful work/energy from these multi-stable molecules has not yet been achieved. To be sure, there have been some ingenious examples14–17 of systems where molecules do act as primitive machines: doubly bistable palindromic rotaxanes bending micro-cantilevers,14 liquid crystals doped with unidirectional molecular rotary motors spinning macroscopic objects,15 liquid crystalline elastomers incorporating photochromic molecules driving macroscopic pulleys,16 and molecular motors propelling nanoparticles in solution.17 These examples are, however, not only few and far between, but they are also rudimentary and, as such, their performance characteristics fall short of being able to fulfill a useful task above and beyond the molecular scale.A question which naturally arises is whether future progress in the field of artificial molecular machines (AMMs) requires only diligent optimization18 of their primitive prototypes or whether a paradigm shift in the manner of our thinking has to take place before AMMs can achieve their potential just like their biological counterparts. It could be argued that the most sophisticated and best understood materials fundamentally are forged at the molecular level by bottom-up protocols: AMMs are no exception. The need for macroscopic functional materials that are composed of many switchable molecules of well-defined constitutions that display synchronous movements is going to become more and more important in the realization of AMMs, just like those robust three-dimensional metal–organic frameworks (MOFs) that have been designed and synthesised of late19 and are now being exploited in a materials context, e.g., for gas storage and separation,20 single-crystal chromatography,21 catalysis,22 and three-dimensional displays23,24 of artificial molecular switches (AMSs) in robust settings. The same requirements of robustness have already been defined for mechanically interlocked molecules (MIMs) which have made their way in the form of bistable catenanes25 and bistable rotaxanes26 into AMSs with applications (i) in molecular electron devices (MEDs) for memory and logic,27 (ii) in nanoelectromechanical systems (NEMS) for actuation of microcantilevers,14,28 and (iii) in mechanized mesoporous silica nanoparticles (MSNPs) for drug delivery.29 Equal opportunities await AMMs provided further experimentation on AMSs is guided by the lessons that become evident from an appreciation of the fundamental theory defining these molecular machines. It follows that the transformation of AMSs into true AMMs requires a paradigm shift in order to identify the appropriate optimization approaches.
An equally prominent and timely question is on what scale AMMs should operate? As we see it, it would be desirable to operate them across all size scales from the molecular level, through the nanoscopic and microscopic, to the macroscopic scales.
In general, there are two parallel routes for further investigation and future progress in the field. The first is to develop AMMs that will perform useful tasks on their own scale, e.g., (i) transport molecular or nanoscopic cargo, (ii) manipulate or “fabricate” other nanostructures, or (iii) facilitate chemical transformations. In the latter context, it would be desirable for the AMMs to address changes in the properties of other functional molecules, e.g., lower their transition state energies and so act like enzymes in nature.30 Perhaps the example in the literature which is the most promising one so far at the molecule-to-molecule level is that described recently by Wang and Feringa31 in which a chiral AMM is employed as a rotary-motor catalyst, capable of controlling chiral space in catalytically asymmetric additions, demonstrating that AMMs can address the stereochemical outcome of a chemical reaction at a molecular level. In principle, any catalyst that can be switched back and forth between several different states can drive a chemical reaction away from equilibrium.32 Expressed in kinetic and thermodynamic terms, the objective in the lower—“chemical”—approach in Fig. 1 is to perturb a local energy minimum of an intermediate, I, such that it cycles between being lower than both SM and P and higher than both SM and P, while also switching the relative barrier heights surrounding I such that the barrier to the left is lower than that to the right when I is low, and the barrier to the left is higher than the barrier to the right when I is high. Carrying out a cycle of switching transfers the red ball from SM to P, where the net energy for the transfer is provided by the switching, but the motion of the ball itself is caused by thermal noise.
 | ||
| Fig. 1 Schematic illustration of two approaches to accomplish the task of moving an object (a marble) from the left-hand well (labeled SM, Starting Material) to the right-hand well (labeled P, Product) via an Intermediate well (labeled I). The upper path shows how this movement can be accomplished mechanically by pushing the object from left to right, perhaps with a finger. If the object is very small, it will be difficult to position it accurately with a “fat finger”. Ineluctable thermal noise, in fact, will make it almost impossible to move the object unless the finger is sticky, but then it will be hard to separate the object from the finger. The lower pathway illustrates a chemical approach in which the energy profile is switched, e.g., by oxidation or reduction, and thermal noise accomplishes the task of moving the object to the central intermediate well. Switching once again allows thermal noise to transfer the object to the right-hand well, and removing the source of the switching resets the system to the original potential, but with the object now residing in the right-hand well. | ||
At the other end of the length-scale lie the machines performing useful operations on scales much larger than the individual AMMs. In this regime, however, it is clear that individual molecules cannot move or manipulate loads orders of magnitudes larger than themselves. We argue that manipulation of macroscopic loads is possible only when the individual AMMs are assembled into larger integrated systems, within which they work in synchronous harmony to perform tasks or build structures at the meso- and macroscopic levels, e.g., AMMs can be viewed as the ultimate molecular actuators. Because the typical distances involving the movable portions of these machines cover the range from Ångstrøms to nanometres, AMMs—when appropriately coupled to other molecules—can be actuated with molecular-scale precision in a manner that's not achievable with conventional hard materials, e.g., piezoelectrics. A particularly relevant usage of actuators based on AMMs is in combination with biomolecules, e.g., AMMs could be attached to biomolecules (enzymes), such that AMMs performing work would change biomolecules' conformations and hence their biological function, providing exquisite control over the properties of biomolecules. Of course, when extended to in vivo applications, a challenge will be to render AMMs biocompatible and operational in water,33 using strategies already employed in conventional drug design (i.e., avoidance of structural features known to be toxic, addition of lipophilic fragments to enhance membrane permeability, etc.) which can be introduced during synthesis of AMMs. It should be pointed out that, in this respect, AMMs should be much more amenable to molecular-scale engineering than any hard materials which pose problems related to biocompatibility and also cannot be easily actuated by chemical signals.
Both individual AMMs and their assemblies can and should be interfaced with nanoscale objects. Recently, it has been demonstrated that AMSs tethered onto metal nanoparticles give rise to composites where the surface properties34–36 are altered, even to the extent that they can act as addressable “sponges” for selective capture and release of one another and other nanoobjects.37 On the back of these early demonstrations, one can envisage hybrid materials in which bundles of AMMs interconnect and mediate mechanical stresses between nearby nanoparticles to give rise to (i) “breathing” nanomembranes or “folding” nanosheets, (ii) plasmonic structures with on-demand control of interparticle electrodynamic coupling and (iii) even materials in which contracting/extending AMMs actuate nanorobotic arms to grip and manipulate other nano-objects. The last example is perhaps the most difficult to contemplate and realize, yet also the most visionary. Indeed, nanoscale-based machinery has been envisaged ever since the days of Feynman and today the Feynman's Grand Prize offers a $250,000 reward to the first persons to create a nanoscale robotic arm, capable of precise positional control. While, in pursuit of this goal, the “top-down” fabrication strategies have so far failed rather dismally, we are convinced that a “bottom-up” approach, utilizing AMMs, can deliver. Engineering a macromolecular architecture capable of robotic function will no doubt be a considerable synthetic challenge. We feel, however, that the time is ripe for such an undertaking—for instance, by combining AMMs with the DNA-origami materials,38 such that the former would provide the actuation within precisely folded DNA nanoscaffolds of the latter.
The dichotomy between the nano- and mesoscales (10−6 m and greater) uses of AMMs is also reflected in the theory that needs to be developed. With individual molecules and assemblies up to the microscale level, fluctuations about the average values must be explicitly considered; for AMMs assembled into larger structures, more deterministic models are appropriate. Although the theoretical framework of these systems has been developed10 in recent years, it is relatively unknown to the “chemical practitioners”—it is thus one of the objectives of this tutorial review to expound the key theoretical concepts, especially those that distinguish simple molecular switches from fully fledged molecular machines.
Overall, we suggest that the future of molecular machinery appears to be bright provided that we can depart from the conventional thinking of these molecules as “miniaturized macroscopic machines” and instead place them into robust environments where the unique chemical aspects of AMMs can be harnessed to greater advantage.
Individual switches and machines
AMSs come in a variety (Fig. 2) of forms14–17,26,28,39–74. Depending on the specific system, AMSs can translate their internal parts (Fig. 2A) from one “station” to another as in bistable rotaxanes,75 can shrink or expand as in the contractions and extensions displayed (Fig. 2B) by bistable daisy chains56–60 or the more conventional cis–trans configurational change (Fig. 2C) brought about by light (and heat) activation in azobenzenes,47–53 or can circumrotate (Fig. 2D) as does (a) the ring under certain circumstances in a [2]rotaxane,64 or as does (b) one of the two rings in a bistable [2]catenane,65,66 or even as do (c) the rotation movements around central double bonds in molecular motors,15,17,62,63,76 or finally (Fig. 2E) can pivot about an internal local axis as in scissor-like molecules.73 Let it be added, however, this list of examples is far from being as exhaustive one.![Popular switches categorized by the type of motion and mode of actuation. Symbols used: ε, efficiency; Δl, distance of actuation; Δϕ, angle of actuation, W (kT); work performed. (A) Shuttling—mode of actuation; chemical: rotaxanes—(i) Δl = 1 nm,39 (ii) Δl = 1.3 nm,40redox: rotaxanes—(i) metal-templated,41 (ii) H-bonded,42 (iii) donor–acceptor,26light: rotaxanes—(i)ε = 0.4, W = 3.65 kT,43 (ii) Δl = 1.3 nm, ε = 0.12,44 (iii) Δl = 0.7 nm.45 (B) Expansion/contraction—mode of actuation; chemical: molecular muscles—(i) Δl = 1.8 nm,56,57 (ii) Δl = 0.9 nm,58,59redox: rotaxanes—Δl = 1.4 nm,14,28light: molecular muscles—(i) Δl ≈ 0.7 nm.60,61 (C) Flapping—mode of actuation; redox: azobenzene,46light: azobenzene16,47–49—(i) ε = 0.1,50 (ii) Δl = 0.7 nm,51 (iii) ε = 0.1, Δl = 0.25 nm, W = 10.9 kT.52,53 Diaryethenes: ε ≈ 0.46, Δϕ = 7°.54Stilbene.55 (D) Rotation—mode of actuation; chemical: molecular rotors (c)—(i) Δϕ = 120°,62 (ii) Δϕ = 360°,63redox: [2]Rotaxane (a)—Δϕ = 180°.64[2]Catenane (b)—(i) Δϕ = 180°,65,66light: [3]Catenane (b)—Δϕ = 360°.67 Spiropyrans (c)—ε = 0.1, Δϕ = 180°.68 Fulgides—ε = 0.12, Δϕ ≈ 90°. Thioindigo—Δϕ ≈ 180°.69 Molecular rotors—(i) ε = 0.07–0.55,70 (ii) Δϕ = 360°.15,17 Nanocars.71 (E) Scissor like motion—mode of actuation; light: molecular scissors:72 (i) Δl = 0.7 nm, ε = 0.1, Δϕ = 49°.73,74](/image/article/2012/CS/c1cs15262a/c1cs15262a-f2.gif) | ||
| Fig. 2 Popular switches categorized by the type of motion and mode of actuation. Symbols used: ε, efficiency; Δl, distance of actuation; Δϕ, angle of actuation, W (kT); work performed. (A) Shuttling—mode of actuation; chemical: rotaxanes—(i) Δl = 1 nm,39 (ii) Δl = 1.3 nm,40redox: rotaxanes—(i) metal-templated,41 (ii) H-bonded,42 (iii) donor–acceptor,26light: rotaxanes—(i)ε = 0.4, W = 3.65 kT,43 (ii) Δl = 1.3 nm, ε = 0.12,44 (iii) Δl = 0.7 nm.45 (B) Expansion/contraction—mode of actuation; chemical: molecular muscles—(i) Δl = 1.8 nm,56,57 (ii) Δl = 0.9 nm,58,59redox: rotaxanes—Δl = 1.4 nm,14,28light: molecular muscles—(i) Δl ≈ 0.7 nm.60,61 (C) Flapping—mode of actuation; redox: azobenzene,46light: azobenzene16,47–49—(i) ε = 0.1,50 (ii) Δl = 0.7 nm,51 (iii) ε = 0.1, Δl = 0.25 nm, W = 10.9 kT.52,53 Diaryethenes: ε ≈ 0.46, Δϕ = 7°.54Stilbene.55 (D) Rotation—mode of actuation; chemical: molecular rotors (c)—(i) Δϕ = 120°,62 (ii) Δϕ = 360°,63redox: [2]Rotaxane (a)—Δϕ = 180°.64[2]Catenane (b)—(i) Δϕ = 180°,65,66light: [3]Catenane (b)—Δϕ = 360°.67 Spiropyrans (c)—ε = 0.1, Δϕ = 180°.68 Fulgides—ε = 0.12, Δϕ ≈ 90°. Thioindigo—Δϕ ≈ 180°.69 Molecular rotors—(i) ε = 0.07–0.55,70 (ii) Δϕ = 360°.15,17 Nanocars.71 (E) Scissor like motion—mode of actuation; light: molecular scissors:72 (i) Δl = 0.7 nm, ε = 0.1, Δϕ = 49°.73,74 | ||
In any event, it is important to recognise that switching at the molecular level is very different from that at the macroscopic level. In the macroscopic world, we have a clear separation between cause and effect where switching is induced by the familiar action of applying a force to a toggle. In the molecular (nanoscopic) world, because of thermal noise, there is no clear cause–effect distinction. Activation of an AMS is achieved by the binding of a ligand, the absorption of a photon, or a change in the external parameters (e.g., pressure, temperature, electrical field strength, etc.) which influence the relative energies of two possible states – “on” and “off”, yet the actual switching between the states is driven ultimately by thermal noise.
It should be recalled that molecular switches are not equivalent to molecular machines. In retrospect, it is not unreasonable that researchers in the field of AMMs have been inclined, during the early days of its development, to claim far too much. After all, a machine sounds much more grandiose than a switch—and it could be argued that the dividing line between the two of them is a rather fine one, with plenty of room for multiple interpretations and with a good deal of overlap between what's a switch and what's a machine. We feel, however, that in order to advance the field to the next level, the distinction between AMSs and AMMs must be more sharply defined and, in terms of synthetic praxis, the key step that must be made is converting switches into machines.
Molecular machines, in sharp contrast to switches, should be able to drive multifarious chemical reactions uphill and away from their “inherent” equilibria, just as motor molecules do in biological systems. Consider, for example, a reversible chemical reaction (Fig. 3) between reactants A and B which at room temperature equilibrates toward a product. Such a chemical reaction can be reversed when sufficient energy is supplied to it by raising the temperature, for example. Alternatively, a switchable, doubly bistable [3]rotaxane, composed of two rings, one functionalised with A and the other with B, that are able to be moved electrochemically along the rotaxanes's dumbbell component between contracted and extended forms, could also provide the energy to drive the reaction uphill into a state that is now away from the reaction's original equilibrium. In the context of organic synthesis one could conceive, for example, of promoting a reverse cycloaddition instead of a cycloaddition or favoring the hydrolysis of a cyclic acetal over its formation, or in both cases, vice versa, depending on where the equilibrium for the particular reaction lies. In any event, the challenge to the synthetic chemist is to reverse the natural course of chemical synthesis wherever possible to relieve kinetic burdens. Chemistry has to direct its focus more and more towards a regime where, as shown in Fig. 1, “switching” is used to steer a reaction along a path in such a way that each molecular transition is spontaneous, and yet at the end of a cycle the reaction has been shifted away from its equilibrium. This concept and how to put it into practice is the thermodynamic reasoning that should be driving the field forward. The task for the synthetic chemist is made all the more daunting by the fact that the number of reactions which have been discovered, or invented, during the past couple of centuries that proceed under thermodynamic control are few and far between compared with those that take place under kinetic control. It will require a fundamental reappraisal of chemical reactivity to halt the trend towards more and more kinetic control (e.g., click chemistry77,78 of the past decade, however useful it might have been and will continue to be in certain arenas), let alone reverse it in favor of a paradigm which is genuinely biomimetic, i.e., doing chemical reactions in the laboratory that are more in tune with those that sustain living organisms. There is more to biomimetic chemistry than catalysis, immensely important as it has been and will continue to be in the quest for doing syntheses away from equilibrium using an integrated systems approach. In such chemical systems of the future, AMMs are going to be the key “control elements” allowing us to manipulate chemical equilibria back and forth.
![AMMs could drive multifarious chemical reactions uphill and away from equilibrium. For example, the cycloadduct in some electrocyclic reactions—e.g., [4 + 2] cycloadditions between dienes (A) and dienophiles (B) in certain Diels–Alder reactions—could be reverted back to staring materials (e.g., A and B) mechanically by coupling the cycloadduct with a redox switchable doubly bistable [3]rotaxane.](/image/article/2012/CS/c1cs15262a/c1cs15262a-f3.gif) | ||
| Fig. 3 AMMs could drive multifarious chemical reactions uphill and away from equilibrium. For example, the cycloadduct in some electrocyclic reactions—e.g., [4 + 2] cycloadditions between dienes (A) and dienophiles (B) in certain Diels–Alder reactions—could be reverted back to staring materials (e.g., A and B) mechanically by coupling the cycloadduct with a redox switchable doubly bistable [3]rotaxane. | ||
In order to convert simple AMSs into usable AMMs, the molecules must be interfaced with their environment to allow for external control and net output of work. To appreciate how this objective might be reached, let us consider a switch (Fig. 4) based on a well-studied class of MIMs we refer to as bistable [c2]daisy chains.79 In this particular system, the bistable molecule, which can exist in two states—contracted (C) or extended (E)—is assumed to be attached to a spring and the relative stabilities of these two states are controlled by oxidation/reduction of one of the stations present in duplicate in the daisy chain.14,28 The orange region near the center between each pair of stations corresponds to the energy barrier that determines the rate of switching between the two stations. When the stations nearest the stoppers are reduced (green), the contracted form of the molecule is favored, and when these stations are oxidized (yellow), the extended form is favored. Extension of the bistable daisy chain (Fig. 4A) stores energy in the spring. The net free energy profile (shown in black) for the molecule/spring system is the sum of the potentials arising from the molecule (a bistable, double-well potential shown in colors to indicate the contributions from the different regions of the molecule) and the spring potential (shown here in dark blue and taken to be a harmonic potential).
![From switches to machines. (A) A graphical representation of a simple, redox switchable, bistable [c2]daisy chain (top) in its contracted and extended forms. The corresponding free energy profiles are illustrated in matching colors beneath each form. If the recognition sites nearer the stoppers are in their reduced (neutral) states (green), they have a greater affinity for the blue rings than do the recognition sites (red) nearer the center of the daisy chain. When the former recognition sites are oxidised (yellow), they have a much weaker affinity for the blue rings which then move to encircle the latter recognition sites (red). When the switchable, bistable [c2]daisy chain (bottom) is attached to a spring, new free energy profiles illustrated above in black represent the sum of the multicolored free energy profiles for the unattached, contracted and extended forms of the [c2]daisy chain and the harmonic potential (blue) of the spring. Wout represents the amount of work stored in the spring. (B) A setup in which switching of the environment from reducing to oxidising conditions is coupled to both extension/contraction and attachment/detachment of the [c2]daisy chain to/from the spring, thereby allowing the system to move in a cycle wherein the extension of the [c2]daisy chain will also expand the spring and store energy. Following the detachment of the bistable [c2]daisy chain, the spring contracts back to its original state, while performing work Wout. This coupling between two separate architectures allows the system to act as a minimal Brownian motor wherein the external driving “pumps” the switching of the bistable [c2]daisy chain between its two different forms. (C) Illustration of how the reduction/oxidation of the green recognition site can be driven by catalytic conversion—. If the contracted form is selective for redox couple 1, and the extended form is specific for redox couple 2, the energy released can be used to drive the system preferentially in a clockwise direction (CA → EA → ED → CD → CA), thereby doing net work on the environment.](/image/article/2012/CS/c1cs15262a/c1cs15262a-f4.gif) | ||
Fig. 4 From switches to machines. (A) A graphical representation of a simple, redox switchable, bistable [c2]daisy chain (top) in its contracted and extended forms. The corresponding free energy profiles are illustrated in matching colors beneath each form. If the recognition sites nearer the stoppers are in their reduced (neutral) states (green), they have a greater affinity for the blue rings than do the recognition sites (red) nearer the center of the daisy chain. When the former recognition sites are oxidised (yellow), they have a much weaker affinity for the blue rings which then move to encircle the latter recognition sites (red). When the switchable, bistable [c2]daisy chain (bottom) is attached to a spring, new free energy profiles illustrated above in black represent the sum of the multicolored free energy profiles for the unattached, contracted and extended forms of the [c2]daisy chain and the harmonic potential (blue) of the spring. Wout represents the amount of work stored in the spring. (B) A setup in which switching of the environment from reducing to oxidising conditions is coupled to both extension/contraction and attachment/detachment of the [c2]daisy chain to/from the spring, thereby allowing the system to move in a cycle wherein the extension of the [c2]daisy chain will also expand the spring and store energy. Following the detachment of the bistable [c2]daisy chain, the spring contracts back to its original state, while performing work Wout. This coupling between two separate architectures allows the system to act as a minimal Brownian motor wherein the external driving “pumps” the switching of the bistable [c2]daisy chain between its two different forms. (C) Illustration of how the reduction/oxidation of the green recognition site can be driven by catalytic conversion— . If the contracted form is selective for redox couple 1, and the extended form is specific for redox couple 2, the energy released can be used to drive the system preferentially in a clockwise direction (CA → EA → ED → CD → CA), thereby doing net work on the environment. . If the contracted form is selective for redox couple 1, and the extended form is specific for redox couple 2, the energy released can be used to drive the system preferentially in a clockwise direction (CA → EA → ED → CD → CA), thereby doing net work on the environment. | ||
Using this example, we make a key—but often overlooked—distinction between an AMS and an AMM. If the bistable daisy chain and the spring are always attached to one another, toggling between the chain's contracted and extended forms is fully reversible and produces no net energy that can be drawn from the system: in other words, the system functions only as a simple switch. In order to function as a machine, in which chemical energy is pumped into the molecule and used to do work on the environment, the spring must be stretched while attached (A) to the molecule, and then allowed to do work by relaxing while detached (D) from the molecule but attached to some load in the environment. One such cycle, in which the individual steps are controlled by redox reactions, is illustrated in Fig. 4B.
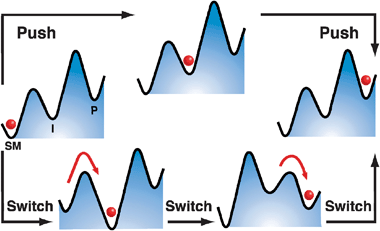
Choosing state ED as a reference (GED = 0), the energies of the states of the bistable [c2]daisy chain molecule are GEA = Wout, GCD = Gred, and GCA = Gox. The net energy change of the system (molecule plus its environment) for each step of a thermodynamic cycle in eqn (1),
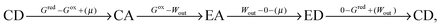 | (1) |
The principle of microscopic reversibility80 for non-photochemical reactions states, “In a reversible reaction, the mechanism in one direction is exactly the reverse of the mechanism in the other direction.” Reflecting on the consequences of this statement, let us consider “half” of the cycle in Fig. 4B—say, from CD to EA. If the most probable path between these two states at some redox potential is through CA, then, at the same redox potential, microscopic reversibility stipulates that the most probable path from EA to CD also leads through CA. In other words, having performed half of the cycle, the system will re-trace the same path backward and most likely will not visit state ED and will not complete a cycle, i.e., no useful work will be done on the environment. Another way to illustrate the unproductive nature of the cycle is to calculate, using a generalized fluctuation–dissipation relation, the relative probabilities for a clockwise vs. counterclockwise cycle.81 Since the change in free energy of the molecular machine is zero through any cycle, the ratio of the probabilities to complete a clockwise (cw) vs. counterclockwise (ccw) cycle can be written in terms of only the changes in the environment, which, for any fixed redox potential, works out to be W > 0 for the cycle in eqn (1). The ratio of the probability for a clockwise to counterclockwise cycle is the exponential of minus the net energy change divided by the thermal energy and is therefore Pcw/Pccw = e−Wout/kBT. Thus, for any fixed redox potential, μ, Pcw < Pccw—i.e., it is more likely for the system to absorb (and dissipate) work from the environment than it is for the system to do work on the environment. This conclusion is consistent with the second law of thermodynamics.
Microscopic reversibility can be circumvented, however, when the conditions are externally modulated or when the AMM acts as a catalyst for a pair of coupled redox reactions  and
and 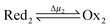 (Fig. 4C). In the example in Fig. 4B, the redox potential is externally driven between a low and a high value. External modulation of the redox potential gives rise to so-called stochastic pumping,10 a concept that is key to understanding the operation of AMMs. Specifically, under reducing conditions (μ < 0), the AMM in Fig. 4B is most likely in state CD, while under oxidizing conditions (μ > 0), it is most likely in state EA. Starting with a reducing environment, a rapid change in oxidizing conditions induces switching of a molecule from CD to EA, predominantly through the intermediate CA, thus storing energy Wout in the spring and absorbing energy Δμ from the chemical environment. After relaxation is complete, the environment is then rapidly changed back to a reducing condition. Under these new environmental circumstances, the molecule is not constrained to retrace the EA → CA → CD path but instead can complete the cycle CD → ED → CA through the intermediate ED. In this cycle, chemical energy, Δμ, is coupled to the performance of work, Wout, on the environment. In the overall cycle resulting from the external modulation, the net energy is Δμ − Wout. Similar directed cycling can also be driven by a non-equilibrium reaction catalyzed as shown in Fig. 4C. If the contracted form is specific for redox couple 1, and the extended form is specific for redox couple 2, the most probable cycle is CD → CA → EA → ED → CD and the chemical driving energy for this cycle is Δμ = Δμ1 − Δμ2. The ratio of the overall probabilities for a clockwise vs. counterclockwise cycle can then be calculated from the generalized fluctuation–dissipation theorem to yield
(Fig. 4C). In the example in Fig. 4B, the redox potential is externally driven between a low and a high value. External modulation of the redox potential gives rise to so-called stochastic pumping,10 a concept that is key to understanding the operation of AMMs. Specifically, under reducing conditions (μ < 0), the AMM in Fig. 4B is most likely in state CD, while under oxidizing conditions (μ > 0), it is most likely in state EA. Starting with a reducing environment, a rapid change in oxidizing conditions induces switching of a molecule from CD to EA, predominantly through the intermediate CA, thus storing energy Wout in the spring and absorbing energy Δμ from the chemical environment. After relaxation is complete, the environment is then rapidly changed back to a reducing condition. Under these new environmental circumstances, the molecule is not constrained to retrace the EA → CA → CD path but instead can complete the cycle CD → ED → CA through the intermediate ED. In this cycle, chemical energy, Δμ, is coupled to the performance of work, Wout, on the environment. In the overall cycle resulting from the external modulation, the net energy is Δμ − Wout. Similar directed cycling can also be driven by a non-equilibrium reaction catalyzed as shown in Fig. 4C. If the contracted form is specific for redox couple 1, and the extended form is specific for redox couple 2, the most probable cycle is CD → CA → EA → ED → CD and the chemical driving energy for this cycle is Δμ = Δμ1 − Δμ2. The ratio of the overall probabilities for a clockwise vs. counterclockwise cycle can then be calculated from the generalized fluctuation–dissipation theorem to yield
 | (2) |
We emphasize again that both stochastic pumping and catalysis circumvent the constraints of microscopic reversibility because of the relaxation from CD to EA under different conditions (oxidizing environment) or by a different chemical mechanism (redox couple 1) than does the relaxation from EA to CD (reducing environment associated with redox couple 2) and thus, the mechanisms need not be the same in the forward and reverse directions. This avoidance of reversibility should be the key design principle that must be obeyed when constructing molecular machines.
Let us now consider some parameters of AMMs. By using chemical design to assure that Gred ≪ 0 and that Gox ≫ 0 for driving by stochastic pumping or to assure that the contracted form is specific for redox couple 1 (kco,1/kco,2 ≫ 1) and that the extended form is specific for redox couple 2 (ker,1/ker,2 ≪ 1), for driving by catalysis, the thermodynamic performance of the AMM can be optimized. In these few limits, the probability for the AMM to undergo “slip” cycles in which mechanical work is dissipated without input/output of chemical energy, or “futile” cycles, in which chemical energy is dissipated without doing work on the environment, is negligible. In the case that slip and futile cycles can be neglected, the efficiency—the fraction of the input chemical energy Δμ that is converted to work Wout—is given82 by
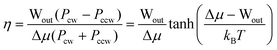 | (3) |
We note that the efficiencies possible—at least in principle—with molecular motions are much higher than the efficiencies of typical automobile engines which convert only 20–30% of the chemical energy of gasoline into mechanical work, or even of the most efficient diesel engine with an efficiency of ca. 50%. The high efficiency of an AMM results from the fact that chemical free energy is converted directly into mechanical work rather than first into heat energy and then into work.
Both stochastic pumping and catalysis circumvent the constraints of microscopic reversibility because of the relaxation from CD to EA under different conditions (oxidizing environment) or by a different chemical mechanism (redox couple 1) than does the relaxation from EA to CD (reducing environment associated with redox couple 2) and thus, the mechanisms need not be the same in the forward and reverse directions.
Another important factor for determining the practicality of AMMs, and one that is ultimately limiting with regard to macroscopic applications of a single AMM, is their capacity to generate power and to store energy. Irrespective of the exact molecular structure, AMSs can be characterized by a double well free energy landscape whose minima correspond to preferred states with and without the external actuating stimulus (Fig. 4A). Typically, the difference between the free energies of these two forms (the difference between red and green wells, Gred, in Fig. 4A) is around 10 kJ mol−1. Oxidation can increase the energy of the “left” well by as much as 4 × 10−18J (2 × 103 kJ mol−1) and hence store this amount of energy in the spring when the molecule undergoes transition to the “right” well. The barrier height that controls the relaxation rate to the contracted form, when the molecule is reduced is typically around (0.8–1.6) × 10−19 kJ, i.e., 20–40 kBT at room temperature. If this relaxation step is the rate-limiting one, the maximum rate of cycling—for the 20 kBT barrier—is 2000 s−1 and the maximum power is only 4 × 10−18 J × 2000 s−1 = 8 × 10−15 W. This maximum power can be contrasted with the continual and reversible noise power exchanged (kBT ≈ 4 × 10−21 J each thermal relaxation time τth ≈ 10−12 s or 4 × 10−9 W) with the molecule's environment. Clearly, individual AMMs are dominated overwhelmingly by thermal effects.
Based on the above considerations, we arrive at two broad conclusions. Firstly, in order to build true AMMs, it is not enough to synthesize switchable molecules, nor is it sufficient to construct a molecule that has a “switchable” rotational or translational degree of freedom. Nowadays, designing and synthesizing such molecules is a relatively straightforward task. The real challenge is interfacing them to their environment in such a way that they draw energy from an external source to perform useful mechanical or chemical work. The grand challenge to the synthetic chemist is thus to engineer a molecular actuator with several well-defined states, where the relative stabilities depend strongly on whether the AMM is or is not coupled to an external load, and where the stabilities can also be switched by an external stimulation. Kinetically, the switching is most efficient if the stimulation rate is slower than the rate of ring movement, but faster than the rate of attaching/detaching the AMM to/from the load.
Secondly, although individual AMMs are suitable for microscopic tasks and can potentially manipulate/actuate other molecules and even nanostructures, the typical powers they are capable of delivering are insufficient to beat the effects of thermal noise and to perform tasks at larger scales. The only means by which these molecules can perform macroscopic work is to order them in mesoscopic arrays. We now turn our attention to this topic.
Machine collections and the benefits of being ordered
Biological systems know these benefits well and virtually all collections of biological motors are spatially (and often temporally) synchronized—dyneins and kinesins align along cytoskeletal fibers, rotary flagellar motors comprise a circular array of ion pumps and other proteins, while skeletal muscles can generate mechanical energy by the cooperative actions of mysosin and actin filaments aligned parallel to one another within sarcomeres building up myofibrils. The spatial arrangement is also crucial for the functioning of the few artificial systems in which molecules have been shown to move large loads. Although switching of an individual bistable molecule is little more than a change in shape—(i) a linear polymer containing azobenzene subunits can give rise (Fig. 5A) to microscopic displacements,52 (ii) a monolayer of doubly bistable palindromic rotaxane molecules can bend28 (Fig. 5B) a microscopic cantilever, and (iii) a liquid crystalline film doped with molecular motors15 can rotate (Fig. 5C) microscopic objects. These examples suggest that, if arranged into large and ordered superstructures, AMMs can indeed perform macroscopic tasks such as transporting a cargo over a distance or generating, in combination, molecular muscles and actuators. An important theoretical observation here is that in such large collections, fluctuations about the average are negligible since noise scales inversely with the square of the number N of individual molecules involved.86 (It must nonetheless be remembered that, even with macroscopic arrays, stochastic events constitute the underlying mechanism by which communication between the macroscopic environment and the system is mediated). As a result of the diminishing importance of the fluctuations for large systems, one can describe the behaviour of macroscopic arrays of AMMs in terms of their bulk thermodynamics. Let us consider, with reference to some possible examples, how one can proceed from a single AMS (Fig. 6A) through progressively more complex ordered structures on surfaces (Fig. 6B and C) to reach finally a true superstructure (Fig. 6D). It is intuitively obvious that a sparse surface coating of the individual chains composed of [c2]daisy chain monomers linked end-to-end will have a small persistence length and the change (Δh) in the length of the polymer chains upon actuation will be much smaller than the number of monomers multiplied by the change (Δl) in the length of the monomer.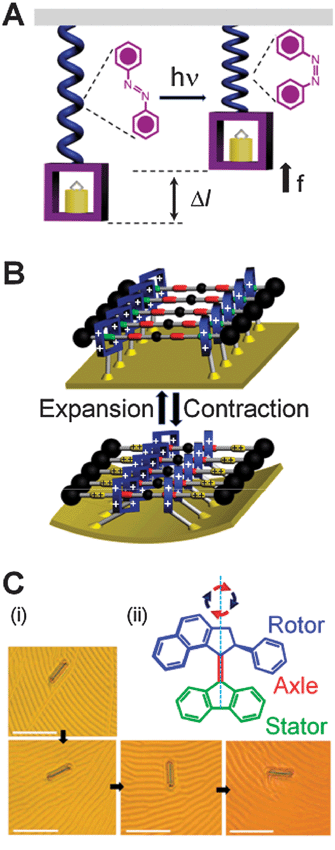 | ||
| Fig. 5 Collections of AMMs can perform mechanical work. (A) Schematic representation of the operation cycle for the polymer containing azobenzene units. Under light irradiation (hν), azobenzenes undergo52trans → cisisomerization, resulting in force f and displacement Δl of the attached object. (B) Electrochemically switchable “palindromic” bistable rotaxanes tethered onto the surface of a gold microcantilever control28 the cantilever's reversible bending. (C) (i) Rotation of a glass rod on a liquid crystal layer doped15 with a “motor” molecule which is switched by UV light. Frames are taken at 15 s intervals and show clockwise rotations of 0, 28, 141, and 226°, respectively. Scale bars: 50 μm. (ii) Structural formula of the AMM. The principal axis indicates the clockwise rotation of the rotor part in a cycle of two photochemical steps (red arrows), causing the isomerization around the central double bond, and two thermal steps (blue arrows). The pictures in (C) are reprinted with permission from ref. 15. | ||
![Machine
assemblies muscle-up. (A) A bistable [c2]daisy chain which can expand and contract and its simplified representation as a cylinder of radius R and length l (upon stimulation, expandable by Δl). The molecules form linear chains of N switching units. These polymers can be attached to a supporting surface as (B) sparsely, as partly coiled polymer brushes or (C) densely packed, as stretched chains. Another possible arrangement is that of muscle-like bundles (D) comprising M chains, and characterized by persistence length λ. This length scales as EI/kT89 where E is the Young's modulus and I is the moment of inertia proportional to the bundle's cross-sectional area, A. This scaling of I with A implies that λ is proportional to the number, M, of individual chains forming a bundle.](/image/article/2012/CS/c1cs15262a/c1cs15262a-f6.gif) | ||
| Fig. 6 Machine assemblies muscle-up. (A) A bistable [c2]daisy chain which can expand and contract and its simplified representation as a cylinder of radius R and length l (upon stimulation, expandable by Δl). The molecules form linear chains of N switching units. These polymers can be attached to a supporting surface as (B) sparsely, as partly coiled polymer brushes or (C) densely packed, as stretched chains. Another possible arrangement is that of muscle-like bundles (D) comprising M chains, and characterized by persistence length λ. This length scales as EI/kT89 where E is the Young's modulus and I is the moment of inertia proportional to the bundle's cross-sectional area, A. This scaling of I with A implies that λ is proportional to the number, M, of individual chains forming a bundle. | ||
When we turn our attention to bundles (Fig. 6D), an intuitive arrangement—reminiscent of muscle fibers—is one in which the switching units form linear chains (n chains at grafting density σ) possibly attached to a supporting surface. Approximating each switch to a cylinder of radius R and length l (upon stimulation, expandable or shrinkable by Δl) and assuming that each chain comprises N switching units (Fig. 6A), the tools of polymer physics can be used to estimate the free energy, G, of the system, and the equilibrium height of the polymer chain, h. In the regime of sparse surface grafting, the chains are partly coiled (Fig. 6B) and the Alexander model87 of polymer brushes can be applied to estimate equilibrium values, Gi ≅ nN(σw/l)2/3kBT and hi ≅ l2/3N(σw)1/3, where superscript i denotes the “initial” state and w is the excluded volume: for the derivation of this and other formulae, see the ESI.† When, upon effecting a stimulus, the switches expand (or contract) from l to l + Δl, then the polymer chain relaxes to a new equilibrium brush height hf ≅ (l + Δl)2/3N(σw/l)1/3. Importantly, the work can be retrieved in this process is
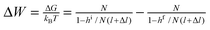 with hf = hi(1 + Δl/l) and hi, hf < Nl. For experimental parameters close to those of the azobenzene example (N = 50, Nl = 90 nm, NΔl = –6 nm, hi = 50 nm), the calculated work this expression predicts is ΔW ≈ 10 kBT which is close to the experimentally observed value.
with hf = hi(1 + Δl/l) and hi, hf < Nl. For experimental parameters close to those of the azobenzene example (N = 50, Nl = 90 nm, NΔl = –6 nm, hi = 50 nm), the calculated work this expression predicts is ΔW ≈ 10 kBT which is close to the experimentally observed value.
The conclusion from these considerations is that, in order to optimize their ability to perform external work, AMMs should be lined up along the direction of actuation as straight as possible. Experimentally, this objective could be achieved, either by packing the chains densely on a surface (Fig. 6C) or by arranging them into muscle-like bundles (Fig. 6D). The close-packed grafts could perform substantial amounts of work—for instance 1014 of 500-mer chains assembled onto a surface of 1 cm2 could perform ΔW = 5 × 10−5 J, enough to actuate a small cantilever or a read/write head. Since ΔW scales with N, even higher values could be achieved with longer grafts. On the other hand, miniaturization of such surface-based polymer systems is problematic. For practical reasons, bundles of chains assembled in solution appear more promising. These bundles can be used as “molecular muscles and actuators” to manipulate various nano- and micromachines, and should be relatively stiff, so that the underlying actions of the AMSs/AMMs translate into “productive” displacement/work. Since the persistence length—i.e., the characteristic distance over which a tubular bundle does not “wiggle” (see Fig. 6D)—is proportional to the number of individual chains forming a bundle89 and is on the order of nanometres for an individual polymer chain (e.g., ∼1 nm for polystyrene and up to about 50 nm for DNA), several hundreds of chains of repeating AMMs need to be bundled together in order to form fibers stiff over micrometre distances. On the other hand, with only a few fibers bundled together, the persistence length would be appropriate for the realization of Feynman's nanoscale robotic arm. Thus, the development of the synthetic methodologies based on self-assembly protocols that bundle even such relatively low numbers of AMM chains together without “lateral” entanglement is certainly a worthy challenge.
Beyond mechanical function
In our discussion so far, we have tacitly assumed that when layered or bundled together, all the constituent molecules perform their switching functions synchronously and without mutual interference. While this mode of operation, “everyone working together,” is ideal for performing mechanical work, different situations can arise if the molecules influence the switching kinetics of their neighbors—these situations are a real terra nova of solid-state chemistry. In the case of two-state switches, a switching of one molecule can either promote or hinder the switching of its neighbors. The first of these cases could be relevant to situations like chemical signaling (Fig. 7A) where an impulse at one location of a monolayer of switches triggers a propagation of a switching “front,” much like in biological calcium waves and related phenomena.88–91 Since for some types of molecules we have been discussing, switching occurs on microsecond time-scales and the linear density of the AMSs within a densely-packed assembly is on the order of 107 molecules per 1 cm, one can approximate the speed of front propagation in mm s−1, a rate which is comparable with the speeds achievable in the so-called active chemical media. By analogy to these media, one can also imagine that periodic forcing of the system would result in the development of spatiotemporal patterns. Such patterns could also form—even without periodic forcing—in situations when there is “negative” coupling between the switching units— i.e., one switch hampers the switching of another. In this case, statistical physical considerations suggest that, if the system is spatially bound—e.g., a crystal92 in Fig. 7B and C—not all the molecules can be in the same state but, instead, one might expect formation of finite size domains within the material. Although these types of phenomena are largely unexplored, we believe that current solid-state synthetic methods are available to realize them. In particular, MOFs93 appear to be very promising scaffolds in which AMSs can be distributed throughout on a regular grid and with distances—and, thus coupling constants!—adjusted precisely by the length of molecular struts. In this spirit but in an even wider context, the marriage between MOFs and AMMs (Fig. 7D) can combine in a truly dialectic way the intuitive ideas of Drexler—inspired by the macroscopic, rigid and robust nature of physics shrunk to the nanoscale—with the more chemically realistic depictions of Smalley, emphasizing the wet, flexible and squelchy nature of organic matter at the molecular scale.94 Indeed, MOFs are robust, rigid, readily available and remarkably amenable to the incorporation of flexible components constituting AMSs3 and AMMs.24 This integration of mesoscale extended structures with pliable mechanically interlocked entities offers a fresh departure for emphasizing the unique advantages of AMMs, while maintaining the stability, reliability, rigidity and robustness associated with macroscopic architectures.![Possible collective phenomena in ensembles of coupled AMMs and synergy with MOF scaffolds. (A) When switching of one molecule causes the neighboring molecules to switch, it can create a domino-like effect propagating as a reaction-front. Here, this situation is illustrated for the case of a monolayer of two-state AMMs.91 (B) When the switching of one unit hampers the switching of its neighbors, one can envision assemblies in which the states of nearby AMMs alternate, much like in an antiferromagnet. This type of behavior has been observed in an experimental solid-state superstructure of a donor–acceptor degenerate [2]rotaxane in (C), where the degenerate [2]rotaxane molecules—composed of a π-electron deficient cyclobis(paraquat-p-phenylene) ring and two π-electron rich 1,5-dioxynaphthalene units—line up in the solid-state92 to form parallel interdigitated donor–acceptor arrays. (D) A scheme of an envisioned24 composite structure combining the robustness of MOFs with the dynamics of MIMs e.g., bistable [2]catenanes. Using this approach, it might be possible to locate, within an extended structural domain built up, for example, from cubes containing rigid struts, AMSs/AMMs in the form of, say, bistable [2]catenanes located at their midpoints. The grey struts, which constitute the cubic framework, supply the robustness, while the pink spheres pin-point the location of the AMSs/AMMs and their moving parts.](/image/article/2012/CS/c1cs15262a/c1cs15262a-f7.gif) | ||
| Fig. 7 Possible collective phenomena in ensembles of coupled AMMs and synergy with MOF scaffolds. (A) When switching of one molecule causes the neighboring molecules to switch, it can create a domino-like effect propagating as a reaction-front. Here, this situation is illustrated for the case of a monolayer of two-state AMMs.91 (B) When the switching of one unit hampers the switching of its neighbors, one can envision assemblies in which the states of nearby AMMs alternate, much like in an antiferromagnet. This type of behavior has been observed in an experimental solid-state superstructure of a donor–acceptor degenerate [2]rotaxane in (C), where the degenerate [2]rotaxane molecules—composed of a π-electron deficient cyclobis(paraquat-p-phenylene) ring and two π-electron rich 1,5-dioxynaphthalene units—line up in the solid-state92 to form parallel interdigitated donor–acceptor arrays. (D) A scheme of an envisioned24 composite structure combining the robustness of MOFs with the dynamics of MIMs e.g., bistable [2]catenanes. Using this approach, it might be possible to locate, within an extended structural domain built up, for example, from cubes containing rigid struts, AMSs/AMMs in the form of, say, bistable [2]catenanes located at their midpoints. The grey struts, which constitute the cubic framework, supply the robustness, while the pink spheres pin-point the location of the AMSs/AMMs and their moving parts. | ||
Conclusions and outlook
In summary, we believe that the combination of structural and dynamic control offers some grand challenges—and, yes, opportunities!—for molecular and macromolecular-level engineering, for self-assembly, and more generally, for chemistry and physics applied to molecules that can reside in and be toggled between several configurations. On the horizon lie new types of “mechanized” enzyme-like mimicks, addressable nanomaterials, nanorobots, and possibly more into the bargain. On the advice of one of the referees of this tutorial review, we have produced (Fig. 8) a roadmap. A new generation of molecular machines and their assemblies could expand the available non-equilibrium toolbox well beyond the Belousov–Zhabotinski or Turing-type media studied95,96 for decades by chemists interested in collective phenomena and complex chemical systems.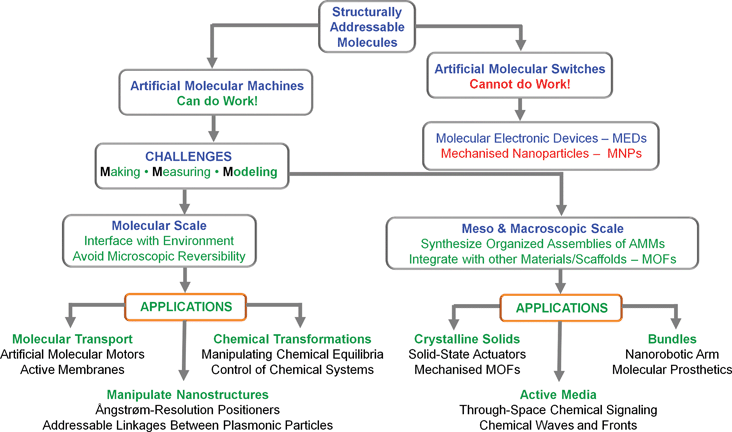 | ||
| Fig. 8 A roadmap outlining some of the challenges facing we chemists, synthetic and otherwise, in transforming structurally addressable molecules into artificial molecular machines (AMMs) and their possible applications at all levels on all length scales. | ||
Acknowledgements
This work was supported by the Non-equilibrium Energy Research Center which is an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0000989.Notes and references
- V. Balzani, A. Credi, F. M. Raymo and J. F. Stoddart, Angew. Chem., Int. Ed., 2000, 39, 3349–3391 CrossRef.
- W. R. Browne and B. L. Feringa, Nat. Nanotechnol., 2006, 1, 25–35 CrossRef CAS.
- C. S. Vogelsberg and M. A. Garcia-Garibay, Chem. Soc. Rev., 2012 10.1039/c1cs15197e.
- E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2007, 46, 72–191 CrossRef CAS.
- V. Balzani, A. Credi and M. Venturi, Molecular Devices and Machines, Wiley, Weinheim, 2nd edn, 2008 Search PubMed.
- J. F. Stoddart, Chem. Soc. Rev., 2009, 38, 1802–1820 RSC.
- J. Michl and E. C. H. Sykes, ACS Nano, 2009, 3, 1042–1048 CrossRef CAS.
- D. Dulić, S. J. van der Molen, T. Kudernac, H. T. Jonkman, J. J. D. de Jong, T. N. Bowden, J. van Esch, B. L. Feringa and B. J. van Wees, Phys. Rev. Lett., 2003, 91, 207402 CrossRef.
- R. D. Astumian, Science, 1997, 276, 917–922 CrossRef CAS.
- R. D. Astumian, Annu. Rev. Biophys., 2011, 40, 289–313 Search PubMed.
- R. Klajn, K. J. M. Bishop, M. Fialkowski, M. Paszewski, C. J. Campbell, T. P. Gray and B. A. Grzybowski, Science, 2007, 316, 261–264 CrossRef CAS.
- Y. B. Zheng, Y. W. Yang, L. Jensen, L. Fang, B. K. Juluri, A. H. Flood, P. S. Weiss, J. F. Stoddart and T. J. Huang, Nano Lett., 2009, 9, 819–825 CrossRef CAS.
- B. Champin, P. Mobian and J.-P. Sauvage, Chem. Soc. Rev., 2007, 36, 358–366 RSC.
- B. K. Juluri, A. S. Kumar, Y. Liu, T. Ye, Y. W. Yang, A. H. Flood, L. Fang, J. F. Stoddart, P. S. Weiss and T. J. Huang, ACS Nano, 2009, 3, 291–300 CrossRef CAS.
- R. Eelkema, M. M. Pollard, J. Vicario, N. Katsonis, B. S. Ramon, C. W. M. Bastiaansen, D. J. Broer and B. L. Feringa, Nature, 2006, 440, 163–163 CrossRef.
- M. Yamada, M. Kondo, J. I. Mamiya, Y. L. Yu, M. Kinoshita, C. J. Barrett and T. Ikeda, Angew. Chem., Int. Ed., 2008, 47, 4986–4988 CrossRef CAS.
- R. A. van Delden, M. K. J. ter Wiel, M. M. Pollard, J. Vicario, N. Koumura and B. L. Feringa, Nature, 2005, 437, 1337–1340 CrossRef CAS.
- H. Hess and E. L. P. Dumont, Small, 2011, 7, 1619–1623 Search PubMed.
- D. J. Tranchemontagne, J. L. Mendoza-Cortes, M. O'Keeffe and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1257–1283 RSC.
- J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- S. B. Han, Y. H. Wei, C. Valente, I. Lagzi, J. J. Gassensmith, A. Coskun, J. F. Stoddart and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 16358–16361 CrossRef CAS.
- A. Corma, H. Garcia and F. X. L. Xamena, Chem. Rev., 2010, 110, 4606–4655 CrossRef CAS.
- Q. W. Li, W. Y. Zhang, O. Š. Miljanić, C. H. Sue, Y. L. Zhao, L. H. Liu, C. B. Knobler, J. F. Stoddart and O. M. Yaghi, Science, 2009, 325, 855–859 CrossRef CAS.
- H. X. Deng, M. A. Olson, J. F. Stoddart and O. M. Yaghi, Nat. Chem., 2010, 2, 439–443 CrossRef CAS.
- C. P. Collier, G. Mattersteig, E. W. Wong, Y. Luo, K. Beverly, J. Sampaio, F. M. Raymo, J. F. Stoddart and J. R. Heath, Science, 2000, 289, 1172–1175 CrossRef CAS.
- J. E. Green, J. W. Choi, A. Boukai, Y. Bunimovich, E. Johnston-Halperin, E. DeIonno, Y. Luo, B. A. Sheriff, K. Xu, Y. S. Shin, H.-R. Tseng, J. F. Stoddart and J. R. Heath, Nature, 2007, 445, 414–417 CrossRef CAS.
- J. R. Heath, Annu. Rev. Mater. Res., 2009, 39, 1–23 CrossRef CAS.
- Y. Liu, A. H. Flood, P. A. Bonvallett, S. A. Vignon, B. H. Northrop, H.-R. Tseng, J. O. Jeppesen, T. J. Huang, B. Brough, M. Baller, S. Magonov, S. D. Solares, W. A. Goddard, C. M. Ho and J. F. Stoddart, J. Am. Chem. Soc., 2005, 127, 9745–9759 CrossRef CAS.
- K. K. Cotí, M. E. Belowich, M. Liong, M. W. Ambrogio, Y. A. Lau, H. A. Khatib, J. I. Zink, N. M. Khashab and J. F. Stoddart, Nanoscale, 2009, 1, 16–39 RSC.
- H. J. Yoon, J. Kuwabara, J. H. Kim and C. A. Mirkin, Science, 2010, 330, 66–69 CrossRef CAS.
- J. B. Wang and B. L. Feringa, Science, 2011, 331, 1429–1432 CrossRef CAS.
- R. D. Astumian and B. Robertson, J. Am. Chem. Soc., 1993, 115, 11063–11068 CrossRef CAS.
- L. Fang, C. Wang, A. C. Fahrenbach, A. Trabolsi, Y. Y. Botros and J. F. Stoddart, Angew. Chem., Int. Ed., 2011, 50, 1805–1809 Search PubMed.
- R. Klajn, L. Fang, A. Coskun, M. A. Olson, P. J. Wesson, J. F. Stoddart and B. A. Grzybowski, J. Am. Chem. Soc., 2009, 131, 4233–4235 CrossRef CAS.
- A. Coskun, P. J. Wesson, R. Klajn, A. Trabolsi, L. Fang, M. A. Olson, S. K. Dey, B. A. Grzybowski and J. F. Stoddart, J. Am. Chem. Soc., 2010, 132, 4310–4320 CrossRef CAS.
- R. Klajn, J. F. Stoddart and B. A. Grzybowski, Chem. Soc. Rev., 2010, 39, 2203–2237 RSC.
- R. Klajn, M. A. Olson, P. J. Wesson, L. Fang, A. Coskun, A. Trabolsi, S. Soh, J. F. Stoddart and B. A. Grzybowski, Nat. Chem., 2009, 1, 733–738 CrossRef CAS.
- A. Kuzuya and M. Komiyama, Nanoscale, 2010, 2, 310–322 RSC.
- J. D. Badjić, V. Balzani, A. Credi, S. Silvi and J. F. Stoddart, Science, 2004, 303, 1845–1849 CrossRef CAS.
- B. Brough, B. H. Northrop, J. J. Schmidt, H.-R. Tseng, K. N. Houk, J. F. Stoddart and C.-M. Ho, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8583–8588 CrossRef CAS.
- F. Durola and J.-P. Sauvage, Angew. Chem., Int. Ed., 2007, 46, 3537–3540 CrossRef CAS.
- A. Altieri, F. G. Gatti, E. R. Kay, D. A. Leigh, D. Martel, F. Paolucci, A. M. Z. Slawin and J. K. Y. Wong, J. Am. Chem. Soc., 2003, 125, 8644–8654 CrossRef CAS.
- J. Berna, D. A. Leigh, M. Lubomska, S. M. Mendoza, E. M. Perez, P. Rudolf, G. Teobaldi and F. Zerbetto, Nat. Mater., 2005, 4, 704–710 CrossRef CAS.
- V. Balzani, M. Clemente-Leon, A. Credi, B. Ferrer, M. Venturi, A. H. Flood and J. F. Stoddart, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1178–1183 CrossRef CAS.
- D. H. Qu, Q. C. Wang and H. Tian, Angew. Chem., Int. Ed., 2005, 44, 5296–5299 CrossRef CAS.
- Z. F. Liu, K. Hashimoto and A. Fujishima, Nature, 1990, 347, 658–660 CrossRef CAS.
- A. Kausar, H. Nagano, T. Ogata, T. Nonaka and S. Kurihara, Angew. Chem., Int. Ed., 2009, 48, 2144–2147 CrossRef CAS.
- H. Koshima, N. Ojima and H. Uchimoto, J. Am. Chem. Soc., 2009, 131, 6890–6891 CrossRef CAS.
- R. Klajn, K. J. M. Bishop and B. A. Grzybowski, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 10305–10309 CrossRef CAS.
- K. Ichimura, S. K. Oh and M. Nakagawa, Science, 2000, 288, 1624–1626 CrossRef CAS.
- V. Ferri, M. Elbing, G. Pace, M. D. Dickey, M. Zharnikov, P. Samori, M. Mayor and M. A. Rampi, Angew. Chem., Int. Ed., 2008, 47, 3407–3409 CrossRef CAS.
- T. Hugel, N. B. Holland, A. Cattani, L. Moroder, M. Seitz and H. E. Gaub, Science, 2002, 296, 1103–1106 CrossRef.
- N. B. Holland, T. Hugel, G. Neuert, A. Cattani-Scholz, C. Renner, D. Oesterhelt, L. Moroder, M. Seitz and H. E. Gaub, Macromolecules, 2003, 36, 2015–2023 CrossRef CAS.
- S. Kobatake, S. Takami, H. Muto, T. Ishikawa and M. Irie, Nature, 2007, 446, 778–781 CrossRef CAS.
- D. H. Waldeck, Chem. Rev., 1991, 91, 415–436 CrossRef CAS.
- M. C. Jimenez, C. Dietrich-Buchecker and J.-P. Sauvage, Angew. Chem., Int. Ed., 2000, 39, 3284–3287 CrossRef CAS.
- P. G. Clark, M. W. Day and R. H. Grubbs, J. Am. Chem. Soc., 2009, 131, 13631–13633 CrossRef CAS.
- L. Fang, M. Hmadeh, J. S. Wu, M. A. Olson, J. M. Spruell, A. Trabolsi, Y. W. Yang, M. Elhabiri, A. M. Albrecht-Gary and J. F. Stoddart, J. Am. Chem. Soc., 2009, 131, 7126–7134 CrossRef CAS.
- J. S. Wu, K. C. F. Leung, D. Benitez, J. Y. Han, S. J. Cantrill, L. Fang and J. F. Stoddart, Angew. Chem., Int. Ed., 2008, 47, 7470–7474 CrossRef CAS.
- R. E. Dawson, S. F. Lincoln and C. J. Easton, Chem. Commun., 2008, 3980–3982 RSC.
- S. Tsuda, Y. Aso and T. Kaneda, Chem. Commun., 2006, 3072–3074 RSC.
- T. R. Kelly, H. De Silva and R. A. Silva, Nature, 1999, 401, 150–152 CrossRef CAS.
- S. P. Fletcher, F. Dumur, M. M. Pollard and B. L. Feringa, Science, 2005, 310, 80–82 CrossRef CAS.
- U. Letinois-Halbes, D. Hanss, J. M. Beierle, J. P. Collin and J.-P. Sauvage, Org. Lett., 2005, 7, 5753–5756 CrossRef CAS.
- D. J. Cardenas, A. Livoreil and J.-P. Sauvage, J. Am. Chem. Soc., 1996, 118, 11980–11981 CrossRef CAS.
- M. Asakawa, P. R. Ashton, V. Balzani, A. Credi, C. Hamers, G. Mattersteig, M. Montalti, A. N. Shipway, N. Spencer, J. F. Stoddart, M. S. Tolley, M. Venturi, A. J. P. White and D. J. Williams, Angew. Chem., Int. Ed., 1998, 37, 333–337 CrossRef CAS.
- D. A. Leigh, J. K. Y. Wong, F. Dehez and F. Zerbetto, Nature, 2003, 424, 174–179 CrossRef CAS.
- F. M. Raymo and M. Tomasulo, J. Phys. Chem. A, 2005, 109, 7343–7352 CrossRef CAS.
- L. Dinescu and R. P. Lemieux, J. Am. Chem. Soc., 1997, 119, 8111–8112 CrossRef CAS.
- B. L. Feringa, J. Org. Chem., 2007, 72, 6635–6652 CrossRef CAS.
- J. F. Morin, Y. Shirai and J. M. Tour, Org. Lett., 2006, 8, 1713–1716 CrossRef CAS.
- T. Muraoka, K. Kinbara and T. Aida, J. Am. Chem. Soc., 2006, 128, 11600–11605 CrossRef CAS.
- T. Muraoka, K. Kinbara and T. Aida, Nature, 2006, 440, 512–515 CrossRef CAS.
- T. Muraoka, K. Kinbara, Y. Kobayashi and T. Aida, J. Am. Chem. Soc., 2003, 125, 5612–5613 CrossRef CAS.
- J. F. Stoddart and H. M. Colquhoun, Tetrahedron, 2008, 64, 8231–8263 CrossRef CAS.
- J.-M. Lehn, Chem.–Eur. J., 2006, 12, 5910–5915 CrossRef CAS.
- V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., Int. Ed., 2002, 41, 2596–2599 CrossRef CAS.
- A. C. Fahrenbach and J. F. Stoddart, Chem.–Asian J., 2011, 6, 2660–2669 Search PubMed.
- L. Fang, M. A. Olson, D. Benitez, E. Tkatchouk, W. A. Goddard and J. F. Stoddart, Chem. Soc. Rev., 2010, 39, 17–29 RSC.
- P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184 CrossRef.
- R. D. Astumian, Phys. Chem. Chem. Phys., 2007, 9, 5067–5083 RSC.
- R. D. Astumian, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1843–1847 CrossRef CAS.
- R. Yasuda, H. Noji, K. Kinosita and M. Yoshida, Cell, 1998, 93, 1117–1124 CrossRef CAS.
- H. Higuchi, E. Muto, Y. Inoue and T. Yanagida, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 4395–4400 CrossRef CAS.
- R. D. Astumian, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19715–19718 CrossRef CAS.
- L. Landau and E. Lifshitz, Statistical Physics, Oxford University Press, 1938 Search PubMed.
- S. Alexander, J. Phys., 1977, 38, 983–987 CAS.
- D. V. Kuznetsov and Z. Y. Chen, J. Chem. Phys., 1998, 109, 7017–7027 Search PubMed.
- A. Y. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, Woodbury, 1994 Search PubMed.
- S. Soh, M. Byrska, K. Kandere-Grzybowska and B. A. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 4170–4198 CrossRef CAS.
- J. J. de Jonge, M. A. Ratner and S. W. de Leeuw, J. Phys. Chem. C, 2007, 111, 3770–3777 CrossRef CAS.
- I. Yoon, O. Š. Miljanić, D. Benítez, S. I. Khan and J. F. Stoddart, Chem. Commun., 2008, 4561–4563 RSC.
- H. Li, M. Eddaoudi, T. L. Groy and O. M. Yaghi, J. Am. Chem. Soc., 1998, 120, 8571–8572 CrossRef CAS.
- R. Baum, C&EN, 2003, 81, 37–42 Search PubMed.
- A. T. Winfree, Science, 1972, 175, 634–636 CrossRef CAS.
- A. M. Turing, Philos. Trans. R. Soc. London, Ser. B, 1952, 237, 37–72 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional theoretical investigations. See DOI: 10.1039/c1cs15262a |
| This journal is © The Royal Society of Chemistry 2012 |