Ultra microelectrodes increase the current density provided by electroactive biofilms by improving their electron transport ability
Diana
Pocaznoi
,
Benjamin
Erable
,
Marie-Line
Delia
and
Alain
Bergel
*
Laboratoire de Génie Chimique CNRS-Université de Toulouse (INPT), 4 allée Emile Monso BP 84234, 31234, Toulouse, France. E-mail: alain.bergel@ensiacet.fr; Tel: +33 5 34 32 36 73
First published on 2nd August 2011
Abstract
Electroactive biofilms were formed from garden compost leachate on platinum wires under constant polarisation at −0.2 V vs.SCE and temperature controlled at 40 °C. The oxidation of 10 mM acetate gave maximum current density of 7 A m−2 with the electrodes of largest diameters (500 and 1000 μm). The smaller diameter wires exhibited an ultra-microelectrode (UME) effect, which increased the maximum current density up to 66 A m−2 with the 25 μm diameter electrode. SEM imaging showed biofilms around 75 μm thick on the 50 μm diameter wire, while they were only 25 μm thick on the 500 μm diameter electrode. Low scan cyclic voltammetry (CV) curves were similar to those already reported for biofilms formed with pure cultures of G. sulfurreducens. Concentrations of the redox molecules contained in the biofilms, which were derived from the non-turnover CVs, were around 0.4 to 0.6 mM, which was close to the value of 1 mM extracted from literature data for G. sulfurreducens biofilms. A numerical model was designed, which demonstrated that the microbial anodes were not controlled here by microbial kinetics. Introducing the concept of average electron transport length made the model well fitted with the experimental results, which indicates rate control by electron transport through the biofilm matrix. According to this model, the UME effect improved the electron transport network in the biofilm, which allowed the biofilm to grow to greater thickness.
Broader contextFor about 10 years microbial fuel cells (MFCs) have been proposed as a promising alternative for producing electrical energy from renewable sources. Many related technologies, such as microbial electrolysis cell, microbial desalination cell, microbial electrosynthesis, and microbial snorkel, have emerged that similarly use the capacity of certain microorganisms to attach on anode surfaces and catalyse the electrochemical oxidation of organic matters. The performance of these technologies now tends to level off because microbial anodes generally provide low current densities, often less than 10 A m−2, with maximum value around 20 A m−2 obtained in scarce cases. This work gave the first experimental demonstration that current density of 66 A m−2 can be reached when microbial anodes are formed on ultra-micro-electrodes (UMEs). A theoretical model was proposed that introduced the “electron transport length” concept to give a simple approach of electron transport inside the biofilm. The model explained that the high current densities were obtained because the UME effect improved the biofilm efficiency for transporting electrons from the microbial cells to the electrode surface. |
Introduction
For about 10 years microbial fuel cells (MFCs) have been proposed as a promising alternative for producing electrical energy from renewable sources. Great advances in MFC technology have been achieved by exploring various microbial communities,1 substrates,2electrode materials/sizes/shapes, and cell designs. Nevertheless, the power densities provided by MFCs now tend to level off around 6.9 W m−2,3 which corresponds to a current density of around 10 A m−2. A recent study has described a MFC producing 30 W m−2, i.e. a current density of 33 A m−2, but it remains the subject of debate.4–7 In well-controlled electrochemical conditions, under constant potential chronoamperometry, microbial cathodes formed with a pure culture of Geobacter sulfurreducens have reached 20.5 A m−2 for the reduction of fumarate.8 This high current density has been obtained at a very low potential, which is not of interest for MFC but is relevant for microbial electrosynthesis. Increasing the current density that can be provided by microbial electrodes remains an essential challenge in developing MFC and other technologies related to microbial electrochemistry.Since their discovery in about 1980, ultra-microelectrodes (UMEs) have been largely implemented in different fields of electrochemistry but they are still rarely used to investigate microbial electrodes. UMEs have been comprehensively described and theorised.9 A UME is generally defined as an electrode having at least one dimension (e.g. width of a band, radius of a disk) equal to or smaller than 25 μm. As the dimension of a UME approaches the order of magnitude of a diffusion layer, mass transfer is enhanced in a way that greatly increases the current density provided by the electrode.
Several works have dealt with millilitre- and microlitre-scale MFCs10,11 with a view to various applications such as power sources for ultra-small electronics12 or implantable medical devices.11–13 Arrays of micro-MFCs coupled to microfluidic systems have also been designed for high-throughput identification of electroactive microorganisms.10–14 Nevertheless, as can be seen in Table 1, these micro-devices do not approach electrode sizes small enough for a UME effect to be observed.15–18 It has sometimes been remarked that small scales can improve the energy output levels,19 but a recent review has evidenced that the existing micro-MFCs generally show lower performance than their millilitre counterparts.11 For example, since the development of the first μL-scale MFC in 2006, which produced 0.023 mW m−2,20 the power density delivered by micro-MFCs has increased only to 4 W m−2.21
| Inoculum | Anode material and area | Anode critical dimension | Anode chamber volume | Substrate | Catholyte | Open circuit voltage/V | J max /mA m −2 | P max /mW m −2 | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| Soil | Platinum (0.0002 cm2) | 25 μm | 150 mL | Acetate | — | — | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— | This work |
| Geobacter sulfurreducens | Gold (0.173 cm2) | 10 μm | 20 mL | Fumarate | — | — | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— | 21 |
| Shewanella oneidensis DSP-10 | Graphite felt (2 cm2) and reticulated vitreous carbon (2 cm2) | — | 1.2 mL | Lactate | Ferricyanide | 0.7 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4000 | 20 |
| Mixed bacterial culture | Carbon cloth (7 cm2) | — | 2.5 mL | Acetate | Air | - | 9000 | 1800 | 3 |
| Geobacter sulfurreducens | Gold (7.8 cm2) | — | 7 mL | Acetate | — | — | — | 688 | 27 |
| Saccharomyces cerevisiae | Gold (1.2 cm2) | — | 15 μL | Glucose | Ferricyanide | 0.49 | 302 | 4 | 13 |
| Saccharomyces cerevisiae | Gold (0.51 cm2) | — | 16 μL | Glucose | Ferricyanide | 0.5 | 150 | 0.023 | 19 |
| Shewanella oneidensis MR-1 | Gold (0.51 cm2) | — | 1.5 μL | Lactate | Ferricyanide | 0.6 | 130 | 1.5 | 12 |
| Shewanella sp. Hac353 | Gold (0.385 cm2) | 7 mm | 650 μL | Tryptic soy broth | Air | — | 6 | 2.7 | 18 |
| Shewanella oneidensis MR-1 | Gold (0.385 cm2) | 7 mm | 650 μL | Tryptic soy broth | Ferricyanide | 0.51 | 5.5 | 0.4 | 14 |
| Shewanella putrefaciens | Gold (0.02 cm2) | 1.6 mm | 10 μL | Lactate | — | — | 3.8 | — | 15 |
| Shewanella oneidensis MR-1 | Gold (−) | 4 mm | 25 μL | Lactate | — | — | — | 29 | 16 |
| Geobacter sulfurreducens | Silicon wafers covered with Ti/Ni/Au (0.25 cm2) | — | 144 μL | Acetate | Ferricyanide | — | — | 65 | 17 |
To our knowledge, UMEs were first introduced into the field of electroactive biofilms by D. R. Bond and co-workers.22 Biofilms of Geobacter sulfurreducens were grown on a uniform gold electrode on the one hand, and on arrays of 10 μm wide lines separated by non-conductive material on the other. Both microbial electrodes were tested for the oxidation of acetate under constant polarisation at +0.242 V vs.SHE. It was observed that the biofilm grew 15 μm outward from the gold micro-lines in a semicylinder, resulting in 4-fold more biomass over the line electrodes than over the uniform electrode. In consequence, the current density (with respect to the gold surface area) was increased from 4 A m−2 on the uniform electrode to 16 A m−2 on the micro-line array. To our knowledge, this article remains the only study that has used microelectrodes to grow electroactive biofilms.
In the present work, platinum wires were used to form wild biofilms from garden compost. These biofilms have already exhibited a good capacity to catalyse the oxidation of dairy wastes on graphite anodes,23,24 and they were implemented here for acetate oxidation under constant potential at −0.2 V vs.SCE (+0.042 V vs.SHE). Decreasing the wire diameter from 1000 to 25 μm showed an UME effect occurring from 50 μm and below, with current density increasing to 66 A m−2 with the 25 μm diameter wire. A theoretical model gave insights into the electron transfer pathway inside the biofilm and the way in which UME affected the biofilm electroactive properties.
Results and discussion
Experimental results
Electroactive biofilms were formed on platinum wires of different diameters from the microbial flora contained in garden compost. Two platinum wires of 2 cm length and diameters of 50 and 500 μm were put into two different electrochemical reactors containing 150 mL of compost leachate with 10 mM acetate. The two experiments were conducted strictly in parallel, at the same time, with the same initial inoculum. The platinum electrodes were maintained at −0.2 V vs.SCE. The current density increased rapidly, reaching 3 A m−2 and 25 A m−2 for the 500 μm and 50 μm diameter electrodes, respectively, at day 3 (Fig. 1). Then, the current decreased because of acetate depletion. Successive additions of 10 mM acetate restarted current generation. Maximum current densities of 7 A m−2, and 32 A m−2 for the 500 μm and 50 μm diameter electrodes respectively, were achieved after the second acetate addition. The perfect synchronism of the two current–times curves should be noted although experiments were performed in different cells.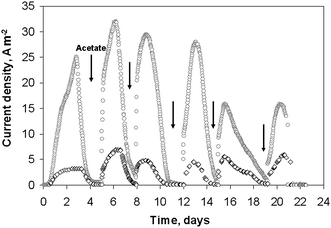 | ||
| Fig. 1 Current densities obtained on 2 wire electrodes colonized by soil bacteria under constant potential −0.2 V vs.SCE: (○) 50 μm diameter, (◇) 500 μm diameter. | ||
At day 21, when the biofilms were still sustaining significant current densities, the electrodes were removed from the reactors and replaced by clean platinum wires. Cyclic voltammetry records with the clean electrodes showed no oxidation current (data not shown), confirming that the biofilms were responsible for the catalysis of acetate oxidation and that current generation was not due to planktonic microorganisms or some metabolites produced.
Four similar experiments were performed with platinum electrodes of diameters 25, 50, 500 and 1000 μm. As with the previous series, the initial lag time was less than 24 hours and the highest current densities were reached after the second addition of acetate (Fig. 2). The biofilms formed on the smallest electrode (25 μm diameter) gave the highest current density, of 66 A m−2. The 50 μm diameter wire provided 19 A m−2, while the two largest wires gave identical current density of 7 A m−2. It was thus confirmed that the current density increased for the smallest wire diameters, while it did not depend on the wire diameter for the largest values (500 and 1000 μm). Moreover, the current densities obtained for these large diameters were identical for both experimental series (7 A m−2). The micro-size effect, which was observed for diameter values of 50 μm but not observed for the 500 μm and 1000 μm diameter wires, perfectly matches the UME theory that determines the critical radius, at which the UME effect starts for a cylindrical electrode, around 25 μm.9 For diameters below 50 μm, the surface curvature is marked enough to affect mass transfer and biofilm formation. For the largest diameters, the surface curvature was no longer significant enough to affect the electrode behaviour, which becomes similar to a planar electrode. The very high current densities obtained with the 25 and 50 μm diameter wires were not due to the nature of the medium or to the electrode material, which gave only 7 A m−2 with wires of large diameter, but to the UME effect.
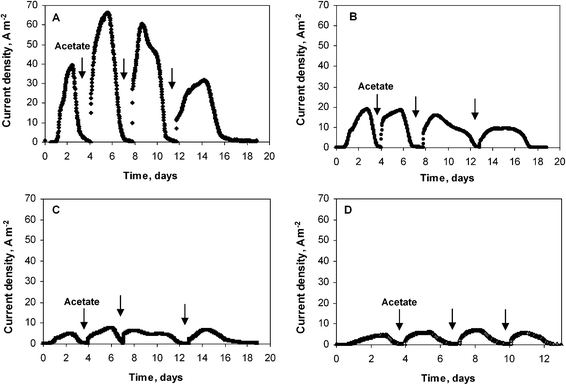 | ||
| Fig. 2 Current density obtained with microbial wire electrodes polarized at −0.2 V vs.SCE. Wire diameter: (A) 25 μm, (B) 50 μm, (C) 500 μm, (D) 1000 μm. | ||
Fig. 3 shows the low scan cyclic voltammograms (CVs) recorded when the current density was a maximum for the four electrodes (day 5 to 6 depending on the electrode). Oxidation started at −0.55 V vs.SCE. Each electrode reached a plateau with a maximal current density from around −0.25 V vs.SCE and these maximum current densities were identical to the values recorded under chronoamperometry at −0.2 V vs.SCE (Fig. 2).
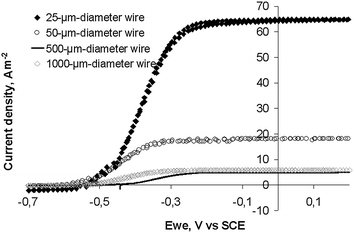 | ||
| Fig. 3 Cyclic voltammograms (1 mV s−1) of soil biofilms formed on platinum wire electrodes of different diameters. CVs were performed at maximum of current density of the chronoamperometric experiments (Fig. 2). | ||
Fig. 4A presents CVs of the 25 μm diameter electrode at day 5 (132 hours) when it was generating the maximum current under chronoamperometry. CVs were performed at 1, 10, 100 mV s−1 and then back at 1 mV s−1. Identical sigmoid shapes were observed at 1 and 10 mV s−1. Moreover the first and last CVs performed at 1 mV s−1 were perfectly identical, showing that the biofilm was not disturbed by the successive scans. Marsili et al. have already shown that fast scan CVs are not destructive for Geobacter sulfurreducens biofilms.25 Here identical results were observed with wild biofilms.
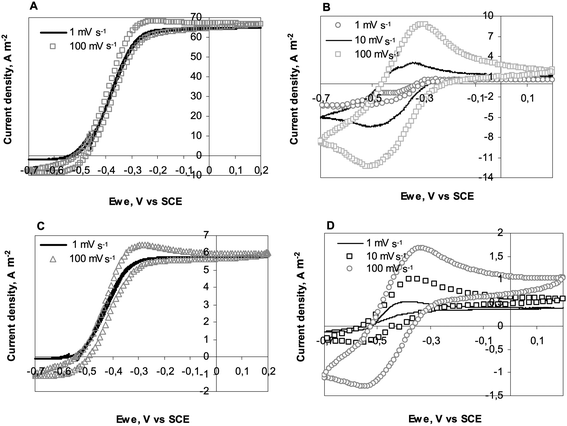 | ||
| Fig. 4 Consecutive cyclic voltammograms at different scan rates recorded on 25 and 1000 μm diameter electrodes: (A) 25 μm diameter wire; CVs performed at maximum current density of CA experiment (Fig. 2A), (B) 25 μm diameter wire; CVs performed after acetate depletion (Fig. 2A), (C) 1000 μm diameter wire; CVs performed at maximum current density of CA experiment (Fig. 2D), (D) 1000 μm diameter wire; CVs performed after acetate depletion (Fig. 2D). | ||
It should also be noted that CVs recorded at 10 and 100 mV s−1 were similar to the low scan CV, with only a small hysteresis phenomenon occurring at 100 mV s−1. Here, recording a CV at 100 mV s−1 did not result in overestimation of the current with respect to the steady-state values. This observation was not related to the electrode diameter, as can be seen in Fig. 4C, which presents CVs recorded on the 1000 μm diameter electrode. The identical quality of the CV curves in the 1 to 100 mV s−1 scan rate range was certainly, to some extent, due to the nature of the biofilm, which was able to achieve steady state conditions even when the potential was varying at 100 mV s−1, and also to the quality of the electrode/biofilm interface. Firstly, platinum electrodes have low double layer capacitance, which reduces hysteresis due to capacitive currents. Secondly, platinum is known to ensure fast electron transfer with cytochromes26 and other proteins.27 The steady current density of 7 A m−2 obtained with the largest electrodes, i.e. in the absence of the UME effect, confirms the suitability of platinum to form electroactive biofilms. Gold electrodes, which have been generally implemented with pure cultures, have led to smaller current density values around 0.9 A m−2 (ref. 28) to 4 A m−2 (ref. 13) with G. sulfurreducens biofilms developed on macro-electrodes. Carbon cloths, graphite felts and other rough or porous electrodes have led to higher currents, but they can hardly be compared to a flat platinum surface because of their high active surface area vs. projected area. The value of 7 A m−2 obtained here on flat electrode surfaces identified platinum as a suitable material for carrying out fundamental investigations of electroactive biofilms.
Four similar consecutive CVs were recorded when almost no current was provided under chronoamperometry (day 7, 168 hours) because of acetate consumption. Fig. 4B and D present CVs recorded with the 25 and 1000 μm diameter wires respectively. In the presence of acetate, the catalytic current corresponded to multiple turnovers of the redox molecules that made up the electron pathway from acetate oxidation to the electrode surface. In the absence of acetate, the peaks observed on CVs were only due to the single oxidation and reduction of the redox compounds contained in the biofilm (non-turnover conditions).29 The CVs were difficult to interpret because they exhibited in both oxidation and reduction directions some significant catalytic currents, which were more clearly visible on the 10 and 100 mV s−1CVs. To explain the catalytic oxidation current, it can be assumed that the acetate was not totally depleted. The cause of the cathodic current remains unclear. It may have resulted from the biofilm-catalysed reduction of components contained in the medium. It must be kept in mind that the garden compost leachate used here as medium had a complex chemical composition. Nevertheless, similar cathodic currents have already been reported even in well-identified artificial media with G. sulfurreducens pure cultures, without any conclusive explanation yet.16
The anodic peak current densities given in Table 2 were calculated by subtracting the value of the catalytic current measured at the potential upper limit (+0.2 V vs.SCE) from the raw peak current. The peak current was approximately proportional to the square root of the potential scan rate (v0.5). Similar dependence has been observed with pure cultures of G. sulfurreducens.29 In some cases a bimodal behaviour (proportionality either to v or to v0.5 depending on the scan rate range)16 or less predictable proportionality to v0.7 has also been observed15 with G. sulfurreducens biofilms. Theoretically, for conventional electrochemical systems, proportionality of the peak current to v indicates that only species adsorbed on the electrode surface take part in electron transfer, while proportionality to v0.5 denotes current control by diffusion of the reactant. As noted by Schröder and co-workers,34 the current knowledge of biofilm electrochemistry is not advanced enough to clearly explain the different behaviours observed with biofilms. Nevertheless, it is generally agreed that dependency of the current peak on v0.5 indicates a diffusion control. In the case of G. sulfurreducens biofilms, it is speculated that electron hopping between the heme centres of the bacterial outer membrane and/or electron transfer inside the biofilm matrix by hopping between linked redox proteins leads to diffusion characteristics.15
| Potential scan rate v/mV s−1 | v 1/2 | Peak current/A m−2 |
|---|---|---|
| 500 μm diameter wire | ||
| 1 | 1 | 0.14 |
| 10 | 3.1 | 0.41 |
| 100 | 10 | 0.66 |
| 50 μm diameter wire | ||
| 1 | 1 | 0 |
| 10 | 3.1 | 2.03 |
| 100 | 10 | 6.63 |
At the end of 19 days polarisation (Fig. 2B and C), the electrodes were observed by scanning electron microscopy. SEM imaging revealed uniform biofilm coverage (Fig. 5A and B) with a large number of microbial cells (Fig. 5C). It seems that the biofilm is connected to the wire surface only by certain sites, while some other parts lie over the metal surface without having direct contact with it (Fig. 5D). A similar structure of biofilm in contact with the electrode surface at some separated sites only has already been observed with electroactive biofilms formed from sediments.30 However, sample preparation that was used before SEM imaging must be taken in mind since it may have significantly disturbed the biofilm structure.
 | ||
| Fig. 5 Scanning electron microscopy of biofilms formed on wire platinum electrodes with different diameters: (A), (C), (D) 50 μm, (B) 500 μm. | ||
The biofilm around the 50 μm diameter wire has an average thickness of 75 μm (Fig. 5A), while it was only about 25 μm on the 1000 μm diameter wire (Fig. 5B). Here, the UME effect clearly affected the biofilm formation. This result is different from the previous observations made by Bond and co-workers who have compared 10 μm large gold micro-lines and uniform rectangular gold electrodes.22 In their case, the biofilm grew 15 μm outward from the micro-line electrodes in a semicylinder shape and, similarly, the biofilm was 15 μm thick over the uniform rectangular electrodes. Biofilms have ceased at similar thickness on both geometries. Formation of the biofilm around the gold micro-lines did not benefit from the faster mass transfers that were facilitated by the UME effect. The authors have suggested that the limitation of biofilm growth may be due to some self-limiting process related to the distance of cells from the electrode surface. It is reported in Bond's work that the biofilm reached its maximum current after around 110 hours, while the maximum was reached in the present study at 60 hours after the initial acetate addition (50 μm diameter electrodes). Assuming that the biofilms were not far from their final size at these times, the biofilm on the gold micro-lines grew by around 15 μm in 110 hours while, in this study, it grew by around 75 μm in 60 hours, which implies that biofilm formation rates were higher by a factor of about 10. It can be assumed that in the previous study, biofilm formation was significantly slow enough to not be limited by mass transfer, which explains why the accelerated mass transfers around the gold micro-lines did not have any effect. In contrast, the faster biofilm growth observed here can result in mass transfer becoming rate-limiting. In the present case, the use of the micro-wire enhanced mass transfer and favoured the biofilm development. There are important differences between the two studies: electrode material, pure culture vs. wild inoculum, different microbial growth rates, richer chemical contents of the medium used here, etc., which can explain the difference in biofilm growth.
The charge due to biofilm oxidation during non-turnover CVs was assessed by integrating the peak currents of the 50 and 500 μm diameter electrodes (Fig. 3). The value of the catalytic currents measured at the potential upper limit (+0.2 V vs.SCE) was subtracted before integrating the oxidation current, which certainly resulted in underestimating the charge related to non-turnover oxidation. The scan performed at 100 mV s−1 gave a charge amount of 22 and 45 μCb for the 50 and 500 μm diameter wires respectively. The corresponding volumes of the biofilms derived from SEM imaging were 5.9 × 10−10 and 8.2 × 10−10 m3. Assuming that the related redox molecules exchange one electron, as is the case for cytochromes and other redox proteins that have been detected in electroactive biofilms (pyocyanine,31flavine32), these charge levels gave concentrations of redox molecules inside the biofilm of around 0.4 and 0.6 mM for the 50 and 500 μm diameter wires respectively.
The same approach was applied to the non-turnover CVs reported by Bond and co-workers at 100 mV s−1 with a pure culture of G. sulfurreducens developed on a gold 10 μm line array electrode.22 It gave 120 μCb for a biofilm volume of 10.8 × 10−10 m3i.e. 1.0 mM of redox molecules inside the biofilm. The results are remarkably consistent even though they are related to very different biofilms: a pure culture of G. sulfurreducens in the one case, a wild multi-species biofilm in the other. Finally, it is worth noting the strong similarities (sigmoid shape of low scan CVs, dependency of non-turnover CV peaks to v0.5) between the results obtained here with wild biofilms implemented in a complex natural medium and results that have been reported for pure cultures of Geobacter sulfurreducens in artificial media.25,29,33,34
Theoretical modelling
We modelled the electrochemical system using the theoretical scheme that Lovley, Tender and co-workers have derived for electroactive microbial biofilms33 from previous theoretical studies devoted to enzyme-modified electrodes.35,36 The bacterial cells oxidise a non-electrode-reactive substrate (acetate here) and transfer the electrons to an electrode-reactive mediator. By similarity with enzymatic mechanisms, the acetate uptake and oxidation by the bacterial cells are assumed to obey Michaelis–Menten kinetics. Acetate uptake is taken into account by an equilibrated reaction, with an equilibrium constant Km that expresses the affinity of the microorganism for acetate. Then the acetate is oxidised through the metabolic pathway with an overall rate constant kcat (Step 1).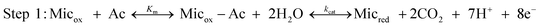 | (1) |
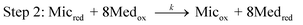 | (2) |
Applying the stationary hypothesis on the Micred species, as is commonly done in enzyme kinetics37 gives:
| [Micred] = [Mic]/(1 + kcat/k[MT] + Km/[Ac]) | (3) |
• [Ac] ≫ Km, which means that acetate concentration is high enough not to be rate-limiting. It has generally been observed that, above values of around 10 mM, the acetate concentration no longer affects the current provided by microbial anodes.
• kcat ≫ k [MT], which means that the metabolic reactions that produce electrons are faster than the final reduction of the membrane-bound or outer-membrane mediator.
According to these hypotheses [Micred] can be assimilated to the total cell concentration [Mic]:
| [Micred] = [Mic] | (4) |
Step 3 is related to the transfer of electrons from the cells to the electrode surface. Different electron transfer mechanisms have been identified. Mediators can be either soluble diffusible species, e.g.phenazines,38thionine,39flavin32 or biofilm-bound redox species, which are linked to the cell outer-membrane and in the extracellular domain of the biofilm. Cytochromes have been widely assumed to play the role of bound-mediators.40 As several mediators undergo mono-electron redox reaction, the model postulates that the 8 electrons produced per acetate molecule reduce 8 mediator molecules. In the present study, we prefer to put the stoichiometric coefficient in this Step 2 (reaction between the cell and mediator) rather than introduce it on the acetate uptake phase (Step 1), as is done in the scheme proposed previously. The final result is unchanged.
On the electrode surface (Step 4) it is assumed, as in Tender–Lovley's model, that the electron transfer rate is fast enough to ensure Nernst equilibrium (reversible system) between the reduced and oxidised forms of the mediator.
| Step 4: Medred ↔ Medox + e− (formal potential E0′) | (5) |
| [Medox]S/[Medred]S = exp {F/RT(E − E0′)} = ξ | (6) |
| [Medred] + [Medox] = [MT] | (7) |
| [Medred]S = [MT]/(1 + ξ) | (8) |
| [Medox]S = [MT]ξ/(1 + ξ) | (9) |
| [Medred] = [MT]/(1 + ξ) | (10) |
| [Medox] = [MT]ξ/(1 + ξ) | (11) |
The total flux of electrons produced by the cells in the whole biofilm is transformed into current:
 | (12) |
For a cylindrical electrode, the current density is obtained by integrating eqn (12) from the electrode surface (r = r0, where r0 is the electrode radius) to the limit of the biofilm (r = r0 + δ, where δ is the biofilm thickness) with the differential volume dv = 2πrLdr and the electrode surface area A = 2πr0L, where L is the wire length:
| j = 8Fk[Mic][MT]ξ/(1 + ξ) δ(1 + δ/2r0) | (13) |
| jL = 8Fk[Mic][MT]δ(1 + δ/2r0) | (14) |
| j = jLξ/(1 + ξ) or (jL − j)/j = ξ | (15) |
| j = 8Fk [Mic][MT]ξ/(1 + ξ)δ | (16) |
| jL = 8Fk[Mic][MT]δ | (17) |
The electrodes of 50 and 500 μm diameter exhibited biofilm thickness (δ) of 75 and 25 μm and provided maximum current density (jL) of 19 and 7 A m−2 respectively. According to eqn (14), the ratio of the maximum current densities should be:
| jL50/jL500 = [Mic]50/[Mic]500 [MT]50/[MT]500 75(1 + 75/50)/25(1 + 25/500) | (18) |
Assuming that concentrations of bacterial cells and redox mediator are equal in both biofilms gives:
| jL50/jL500 = 75(1 + 75/50)/25(1 + 25/500) = 7.1 | (19) |
Actually the term δ(1 + δ/2r0) is equal to the ratio of the biofilm volume to the electrode surface area:
| δ(1 + δ/2r0) = π((r0 + δ)2 − r02)L/2πr0L | (20) |
This means that, in the case of control by a microbial step, the current would depend directly on the volume of the biofilm. This case was reported by Bond and co-workers.22 They showed that the biofilm formed around gold micro-lines gave a 4-fold higher current density than that of the biofilm formed on a flat gold surface with equal total area, because the volume around the micro-lines was 4-fold larger. In this case it can be assumed that the microbial anodes were controlled by the microbial kinetics. Other studies have also presented cases of microbial control with complex microbial population.41 The conclusion appears to be different for the present work.
Electron hopping has been described and theorised for chemically modified electrodes, in which electroactive groups are attached to the electrode-bound film. Commonly, an apparent diffusion coefficient DE is introduced, which is composed of the contributions from the physical movement of the diffusible mediator and from the hopping process.9 The current density is given by flux of Medred at the electrode surface:
| j = FDEd[Medred]/dr|r = r0 | (21) |
We propose a simplified scheme of the electroactive biofilm here by introducing an average electron transport length (δE). According to this scheme, for each cell the length of the electron transport path is equal to the same average value. In this simple model, the electroactive biofilm is seen as an “electron diffusion layer” adjacent to the electrode surface with thickness δE, and the bacterial cells at the forefront of this domain. In the absence of a generation term in the diffusion space, the continuity equation in cylindrical coordinates is:
| d/dr(rd[Medred]/dr) = 0 | (22) |
• Nernst equilibrium at the electrode surface:
| r = r0: [Medred] = [MT]/(1 + ξ) | (23) |
• If the process is limited by the electron transport rate, the bacterial cells ensure the maximum concentration of Medred at the Frontier of the diffusion layer:
| r = r0 + δE: [Medred] = [MT] | (24) |
Integration of eqn (22) gives the Medred concentration profile in the electron diffusion layer and then eqn (21) leads to the expression of j:
| j = FDE[MT]ξ/(1 + ξ)/(r0 ln (1 + δE/r0)) | (25) |
As usual, when E ≫ E0′ jL is:
| jL = FDE[MT]/(r0 ln (1 + δE/r0)) | (26) |
| j = jLξ/(1 + ξ) or (jL − j)/j = ξ | (27) |
Eqn (27) was identical to eqn (15). As a first conclusion, the shapes of the j vs. E curves are identical whatever the rate-limiting hypothesis and consequently these curves cannot help in discriminating between metabolism or electron transport control.
Eqn (27) was used to fit the experimental CV obtained at 1 mV s−1 with the 25 μm diameter electrode (Fig. 6). The best fitting was given with JL = 65.2 A m−2 and E0′ = −0.38 V vs.SCE (−0.14 V vs.SHE). The E0′ value is consistent with the values around −0.15 V vs.SHE that have been derived by similar fitting for G. Sulfurreducens pure cultures16 or complex populations.41 The theoretical curve was not exactly superimposed to the experimental one. Replacing the reversible (Nernst) equilibrium (eqn (23)) by an irreversible boundary condition resulted in better fitting with the same E0′ and jL values and a transfer coefficient (α) of 0.6 (Fig. 6). The electron transfer was likely irreversible rather than reversible at the electrode surface. This refinement of the model is not detailed here because it does not change the expression of the limit current densities (jL), on which the conclusions are based.
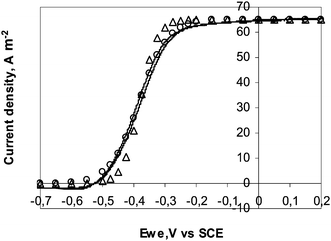 | ||
| Fig. 6 Current–potential curve recorded with the 25 μm diameter electrode at 1 mV s−1 (Δ) theoretical points according to the electron transport limiting hypothesis (hypothesis B) with jL = 65.2 A m−2, E0′ = −0.38 V vs.SCE; (○) theoretical points obtained by replacing the Nernst equilibrium by an irreversible electrochemical oxidation at the electrode surface with α = 0.6. | ||
When r0 ≫ δ, the effect of electrode curvature vanishes and j tends to the expression valid for planar electrodes:
| j = FDE/δE[MT]ξ/(1 + ξ) | (28) |
The electrodes of 50 and 500 μm diameter provided 19 and 7 A m−2, respectively. According to eqn (26) the ratio of the maximum current densities should be:
| jL50/jL500 = 250 ln (1 + δE500/250)/25 ln (1 + δE50/25) | (29) |
The previous study implementing UME for biofilm formation22 did not show any specific UME effect. The 4-fold higher current recorded on the micro-line electrodes was explained by the 4-fold greater biomass that shared each micro-line compared to the rectangular geometry. Moreover, the biofilms reached the same thickness regardless of the electrode geometry: they stopped at 15–20 μm around (micro-line electrodes) or 15–20 μm over (rectangular electrode) the electrode surface.
These differences compared to the present results are not basically contradictory. Firstly, the biofilms grew around 10-times more slowly in the previously reported study, which can explain the absence of sensitivity to mass transfer conditions and, in consequence, the absence of a true UME effect on the micro-line electrodes. Moreover, the biofilms were controlled by the microbial kinetics, and possible differences in electron transport capacity could consequently not be detected. Finally, the authors hypothesise that biofilm growth stops at the same thickness regardless of the electrode geometry because of a self-limitation process. This self-limitation may be inherent to the distance cells are located from the electrode surface. This hypothesis remains consistent with the results obtained here. In the present study, the UME effect on the biofilm was to improve its capacity for electron transport. This modification allowed the biofilm to grow to a larger distance from the electrode surface: biofilms were 75 μm thick on 50 μm electrodes that exhibited an UME effect, while they stopped at 25 μm on the 500 μm electrodes. In both studies the biofilm thickness was controlled by its capacity for long-range electron transfer. Despite very different conditions and different biofilm behaviours, both studies may lead to very similar basic hypotheses.
Experimental
Soil samples
Garden compost for organic cultivation (Eco-Terre) was used as the source of electrochemically active microorganisms. A solution of 60 mM potassium chloride was added to 1 L of garden compost and left for 24 hours under stirring. The mixture was centrifuged and 10 mM acetate was added into the final leachate, which was used as medium for the electrochemical reactors. The initial pH was around 7.5 and it increased to 8.5–9 during the experiments. All the experiments were performed at 40 °C, which has been determined as the optimal temperature.44Platinum electrode preparation
Platinum microelectrodes were constructed with platinum wires inserted into conical polyethylene tubes of approximately 1 mm diameter at the tip end. The tubes were filled with insulating resin. Platinum wires of four different diameters were used: 25, 50, 500 and 1000 μm. Each wire electrode was 2 cm long. Each electrode was tested before use by cyclic voltammetry in 25 mM potassium hexacyanidoferrate(II) solution containing 100 mM potassium chloride.Electrochemical set-up
A three-electrode system was used in all electrochemical experiments. The electrochemical reactors contained 150 mL soil leachate. The platinum wire working electrodes were polarised at −0.2 V vs. a saturated calomel reference electrode (SCE potential +0.242 vs.SHE) with a platinum grid as a counter electrode using a VMP potentiostat (Bio-logic SA). Chronoamperometry was sometimes interrupted to make cyclic voltammetry records at 1, 10 and 100 mV s−1 in the range −0.7 to +0.2 V vs.SCE.Scanning electron microscopy
Electrodes were fixed in phosphate buffer (400 mM, pH = 7.4) with 4% glutaraldehyde. Samples were rinsed in phosphate buffer containing saccharose (0.4 M). Electrodes were then incubated for 1 hour in phosphate buffer with 2% osmium tetroxide solution and saccharose. The samples were dehydrated by being immersed in increasing concentrations of acetone (50%, 70%, 100%), then in acetone and hexamethyldisilazane (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50), and in 100% hexamethyldisilazane (HMDS). The last batch of HMDS was dried until complete evaporation. The samples were observed with a LEO 435 VP scanning electron microscope.
50), and in 100% hexamethyldisilazane (HMDS). The last batch of HMDS was dried until complete evaporation. The samples were observed with a LEO 435 VP scanning electron microscope.
Conclusions
Wild biofilms were formed from garden compost leachate for acetate oxidation under constant potential on platinum electrodes. Stationary current density around 7 A m−2 was reached without any UME effect and low capacitive currents were observed in CVs up to 100 mV s−1, showing that platinum is a suitable material for investigating microbial biofilms.The platinum wires exhibited a UME effect for diameters of 50 μm and smaller, in accordance with UME theory. Electrode of 25 μm diameter led to current densities up to 66 A m−2 at −0.2 V vs.SCE. This value represents a real advance for microbial electrode development, because it demonstrated that far higher values than reported so far can be reached by optimising the biofilm structure. This work represents significant progress towards the theoretical value of 280 A m−2, which has recently been proposed as a possible target.45
Theoretical modelling showed that the microbial anode was not controlled here by the microbial kinetics but by electron transport through the biofilm matrix. The UME effect increased the current density provided by the biofilm by improving the efficiency of the electron transport network in the biofilm. Focusing on the electron transport mechanisms inside the biofilm is consequently a promising avenue for improving microbial anodes.
Acknowledgements
The authors thank Marie-Line de Solan (LGC) for her help with SEM images, Luc Etcheverry (LGC) for technical support and Dr Bibiana Cercado for discussions on biofilm formation procedures. This research was part of the “Agri-Elec” project funded by the French National Research Agency (ANR-08-BioE-001).Notes and references
- B. E. Logan, Nat. Rev. Microbiol., 2009, 7, 375–381 CrossRef CAS.
- D. Pant, G. Van Bogaert, L. Diels and K. Vanbroekhoven, Bioresour. Technol., 2010, 101, 1533–1543 CrossRef CAS.
- Y. Z. Fan, E. Sharbrough and H. Liu, Environ. Sci. Technol., 2008, 42, 8101–8107 CrossRef CAS.
- A. V. Samrot, P. Senthilkumar, K. Pavankumar, G. C. Akilandeswari, N. Rajalakshmi and K. S. Dhathathreyan, Int. J. Hydrogen Energy, 2010, 35, 7723–7729 CrossRef CAS.
- F. Rezaei, T. L. Richard and B. E. Logan, Int. J. Hydrogen Energy, 2010, 35, 10635 CrossRef CAS.
- N. Rajalakshmi, Int. J. Hydrogen Energy, 2010, 35, 10636–10637 CrossRef CAS.
- L. Angenent, M. Rosenbaum, R. Rozendal, K. Rabaey, B. Logan and U. Schröder, Int. J. Hydrogen Energy, 2011, 36, 9396–9397 CrossRef CAS.
- C. Dumas, R. Basseguy and A. Bergel, Electrochim. Acta, 2008, 53, 2494–2500 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods, John Wiley & Sons, New York, 2nd edn, 2001, vol. 1, ch. 5 and 14, p. 169 Search PubMed.
- F. Qian and D. E. Morse, Trends Biotechnol., 2010, 29, 62–69 CrossRef.
- H.-Y. Wang, A. Bernarda, C.-Y. Huang, D.-J. Lee and J.-S. Chang, Bioresour. Technol., 2011, 102, 235–243 CrossRef CAS.
- F. Qian, M. Baum, Q. Gu and D. E. Morse, Lab Chip, 2009, 9, 3076–3081 RSC.
- C. P. B. Siu and M. Chiao, J. Microelectromech. Syst., 2008, 17, 1329–1341 CrossRef CAS.
- H. J. Hou, L. Li, P. de Figueiredo and A. Han, Biosens. Bioelectron., 2011, 26, 2680–2684 CrossRef CAS.
- S. R. Crittenden, C. J. Sund and J. J. Sumner, Langmuir, 2006, 22, 9473–9476 CrossRef CAS.
- Y. P. Chen, Y. Zhao, K. Q. Qiu, J. Chu, R. Lu, M. Sun, X. W. Liu, G. P. Sheng, H. Q. Yu, J. Chen, W. J. Li, G. Liu, Y. C. Tian and Y. Xiong, Biosens. Bioelectron., 2011, 26, 2841–2846 CrossRef CAS.
- D. Davila, J. P. Esquivel, N. Sabate and J. Mas, Biosens. Bioelectron., 2011, 26, 2426–2430 CrossRef CAS.
- H. J. Hou, L. Li, Y. Cho, P. de Figueiredo and A. Han, PLoS One, 2009, 4, 6570–6578 Search PubMed.
- I. Ieropoulos, J. Greenman and C. Melhuish, Bioelectrochemistry, 2010, 78, 44–50 CrossRef CAS.
- M. Chiao, K. B. Lam and L. W. Lin, J. Micromech. Microeng., 2006, 16, 2547–2553 CrossRef CAS.
- B. R. Ringeisen, E. Henderson, P. K. Wu, J. Pietron, R. Ray, B. Little, J. C. Biffinger and J. M. Jones-Meehan, Environ. Sci. Technol., 2006, 40, 2629–2634 CrossRef CAS.
- Y. Liu, H. Kim, R. Franklin and D. R. Bond, Energy Environ. Sci., 2010, 3, 1782–1788 CAS.
- B. Cercado-Quezada, M.-L. Delia and A. Bergel, Bioresour. Technol., 2010, 101, 2748–2754 CrossRef CAS.
- B. Cercado-Quezada, M.-L. Délia and A. Bergel, J. Appl. Electrochem., 2010, 40, 225–232 CrossRef CAS.
- E. Marsili, J. B. Rollefson, D. B. Baron, R. M. Hozalski and D. R. Bond, Appl. Environ. Microbiol., 2008, 74, 7329–7337 CrossRef CAS.
- M. M. Correia dos Santos, P. M. Paes de Sousa, M. L. Simões Gonçalves, H. Lopes, I. Moura and J. J. G. Moura, J. Electroanal. Chem., 1999, 464, 76–84 CrossRef CAS.
- A. Bergel and M. Comtat, J. Electroanal. Chem., 1991, 302, 219–231 CrossRef CAS.
- H. Richter, K. McCarthy, K. P. Nevin, J. P. Johnson, V. M. Rotello and D. R. Lovley, Langmuir, 2008, 24, 4376–4379 CrossRef CAS.
- E. Marsili, J. Sun and D. R. Bond, Electroanalysis, 2010, 22, 865–874 CAS.
- B. Erable and A. Bergel, Bioresour. Technol., 2009, 100, 3302–3307 CrossRef CAS.
- K. Rabaey, N. Boon, S. D. Siciliano, M. Verhaege and W. Verstraete, Appl. Environ. Microbiol., 2004, 70, 5373–5382 CrossRef CAS.
- E. Marsili, D. B. Baron, I. D. Shikhare, D. Coursolle, J. A. Gralnick and D. R. Bond, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3968–3973 CrossRef CAS.
- H. Richter, K. P. Nevin, H. F. Jia, D. A. Lowy, D. R. Lovley and L. M. Tender, Energy Environ. Sci., 2009, 2, 506–516 CAS.
- K. Fricke, F. Harnisch and U. Schroder, Energy Environ. Sci., 2008, 1, 144–147 CAS.
- I. Katakis and A. Heller, Anal. Chem., 1992, 64, 1008–1013 CrossRef CAS.
- E. V. J. M. Saveant, Electrochim. Acta, 1965, 10, 905–920 CrossRef.
- I. H. Segel, Enzyme Kinetics, Behaviour and Analysis of Rapid Equilibrium and Steady-state Enzyme Systems, John Wiley & Sons, New York, 1st edn, 1993, vol. 1, ch. 9, p. 505 Search PubMed.
- K. Rabaey, N. Boon, M. Hofte and W. Verstraete, Environ. Sci. Technol., 2005, 39, 3401–3408 CrossRef CAS.
- A. K. Shukla, P. Suresh, S. Berchmans and A. Rajendran, Curr. Sci., 2004, 87, 455–468 CAS.
- D. R. Lovley, Curr. Opin. Biotechnol., 2008, 19, 564–571 CrossRef CAS.
- C. I. Torres, A. K. Marcus, P. Parameswaran and B. E. Rittmann, Environ. Sci. Technol., 2008, 42, 6593–6597 CrossRef CAS.
- A. K. Marcus, C. I. Torres and B. E. Rittmann, Biotechnol. Bioeng., 2007, 98, 1171–1182 CrossRef CAS.
- C. I. Torres, A. K. Marcus, H. S. Lee, P. Parameswaran, R. Krajmalnik-Brown and B. E. Rittmann, FEMS Microbiol. Rev., 2010, 34, 3–17 CrossRef CAS.
- B. Cercado-Quezada, M. L. Delia and A. Bergel, J. Appl. Electrochem., 2010, 40, 225–232 CrossRef CAS.
- L. Pons, M. L. Delia and A. Bergel, Bioresour. Technol., 2011, 102, 2678–2683 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
