Non-Langevin bimolecular recombination in a silole-based polymer:PCBM solar cell measured by time-resolved charge extraction and resistance-dependent time-of-flight techniques
Tracey M.
Clarke
*a,
Jeff
Peet
b,
Patrick
Denk
c,
Gilles
Dennler
bd,
Christoph
Lungenschmied
b and
Attila J.
Mozer
*a
aARC Centre of Excellence for Electromaterials Science, Intelligent Polymer Research Institute, University of Wollongong, North Wollongong, NSW 2500, Australia. E-mail: tclarke@uow.edu.au; attila@uow.edu.au
bKonarka Technologies, 116 John St., Suite 12, Lowell, Massachusetts 01852, USA
cKonarka Austria, Altenbergerstrasse 69, A-4040, Linz, Austria
dIMRA Europe, 220, rue Albert Caquot - BP 213, 06904, Sophia-Antipolis Cedex, France
First published on 31st October 2011
Abstract
The silole-based non-Langevin conjugated polymer KP115 has been used to demonstrate that circuit resistance is a crucial parameter in time-of-flight measurements of organic photovoltaic cells, providing a resistance-dependent bimolecular recombination coefficient. The origin of this behaviour is the biphasic decay dynamics present in KP115:PCBM devices (observed using a novel time-dependent charge extraction technique), which time-of-flight cannot accurately characterise.
Broader contextThe silole-based conjugated polymer KP115 is receiving significant attention recently due to its strongly reduced (non-Langevin) recombination behaviour. In this communication, we use KP115:PCBM organic photovoltaic devices to compare two different charge extraction techniques that provide information on the bimolecular recombination coefficient, β. A strongly resistance-dependent β was observed using the time-of-flight (TOF) technique; this was attributed to the biphasic decay dynamics measured using a novel time-resolved switch-based charge extraction technique. The conclusion that TOF cannot accurately describe the complex bimolecular recombination mechanisms involved in this system is important for the organic photovoltaics field. Due to the TOF technique rapidly gaining wider popularity, it is important to note that the resistance-dependence we observe in TOF is an important limitation of this technique. It indicates that in order to fully describe the bimolecular recombination behaviour, it is vital to utilise a variety of charge extraction techniques, such as the novel switch-based time-resolved one introduced here. |
Bulk heterojunction organic photovoltaic cells have been steadily increasing in power conversion efficiencies over the past few years, with efficiencies in excess of 8–9% reported recently.1–3 In order to further improve these devices, it is important to understand the factors that affect device performance, such as the various loss mechanisms present. Of these losses, recombination of the charges prior to collection at the electrodes has been identified as one of the most significant.4,5 Geminate recombination most often refers to a monomolecular relaxation of the charges whilst they are still coulombically bound, although a more general definition simply requires recombination of charges generated from the same exciton. In contrast, bimolecular recombination involves recombination of fully dissociated charges created from different excitons. This latter process is known to be a significant limiting factor of the open-circuit voltage (Voc)6 and also influences the fill factor.7
Due to the hopping transport typical of the organic materials used in solar cells and consequent low charge carrier mobilities, Langevin bimolecular recombination often dominates in these systems.4,8,9 The Langevin recombination coefficient, βL, is proportional to the charge carrier mobility, μ, via βL = e(μp + μn)/εε0. Although MDMO-PPV:PCBM solar cells exhibit behaviour consistent with Langevin recombination, annealed P3HT:PCBM cells do not.9,10 They typically show a significant departure from this type of recombination, with a bimolecular recombination coefficient, β, several orders of magnitude lower than that expected for Langevin recombination. Recently, however, it has been reported that unannealed P3HT:PCBM possesses a β much closer to that of Langevin recombination.10 Given that the efficiencies of annealed P3HT cells are usually substantially higher than that of unannealed cells,11–13 this result implies that this parameter has an appreciable effect on solar cell performance.
A number of techniques exist to investigate bimolecular recombination and/or mobility, including transient absorption spectroscopy (TAS), time-of-flight (TOF) and photo-induced charge extraction by linearly increasing voltage (photo-CELIV).9,14,15TOF is one of the most widely used and allows measurement of charge transport in low mobility systems. The main concept behind this technique is that, in current mode under surface generation conditions, a sheet of photoinduced charge carriers will travel through the active layer of thickness d with a characteristic transit time, ttr, where ttr = d2/μU0 (U0 is the applied voltage). When bimolecular recombination is present, the extracted charge saturates at high light intensities. This allows the ratio between the bimolecular recombination coefficient and the Langevin recombination coefficient (β/βL) to be directly determined, as shown by Pivrikas et al.:8
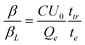 | (1) |
An important limitation of TOF is that eqn (1) provides only a single value for β that is valid for a particular set of conditions (charge density and extraction time, for example). However, previous reports on P3HT:PCBM devices have shown that β is dependent upon charge carrier density and/or time.6,17 This raises the question of what β the TOF technique is really measuring; it is this topic that we will address in this communication. We therefore present recombination results obtained from TOF of a poly[(4,4′-bis(2-ethylhexyl)dithieno[3,2-b:2′,3′-d]silole)-2,6-diyl-alt-(2,5-bis(3-tetradecylthiophen-2-yl)thiazolo-5,4-d-thiazole)-2,5-diyl] (KP115) solar cell blended with PCBM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by weight) that show a strong dependence on the circuit resistance. Furthermore, we introduce a time-resolved charge extraction technique that reveals biphasic decay dynamics in KP115:PCBM and a time-dependent β, thereby highlighting the limitations of TOF in describing such complex recombination behaviour.
2 by weight) that show a strong dependence on the circuit resistance. Furthermore, we introduce a time-resolved charge extraction technique that reveals biphasic decay dynamics in KP115:PCBM and a time-dependent β, thereby highlighting the limitations of TOF in describing such complex recombination behaviour.
KP115 (the structure is displayed in Fig. 1a) is a new silicon-bridged push/pull polymer that produces relatively high efficiencies of ∼5%, similar to other polymers of this type.18,19 Furthermore, this polymer is particularly promising as it is capable of producing high fill factor photovoltaic cells (>60%) with active layers greater than 200 nm thick.20 This characteristic is vital for commercial viability but is rarely observed. Previous work has revealed that, similar to annealed P3HT:PCBM, KP115:PCBM solar cells possess non-Langevin recombination.21 This enables a long charge carrier drift length (and diffusion length), which ensures that the resultant solar cells are not limited by thickness and thicker active layers can be employed. KP115:PCBM is one of the few polymer-based systems that exhibits this highly beneficial behaviour.
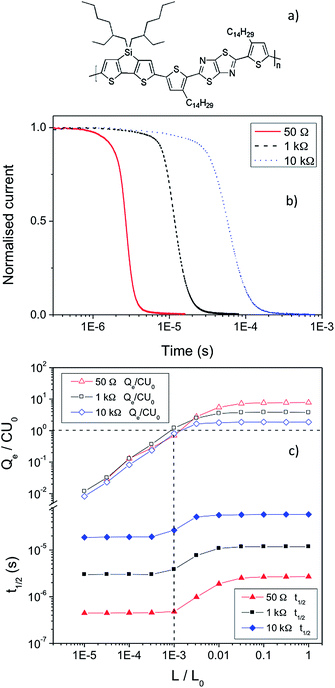 | ||
Fig. 1 a) The structure of KP115. b) The normalised TOF current decays of KP115:PCBM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) devices at high light intensity as a function of resistance. c) Analysis of the TOF results as a function of excitation density, using the three different resistances (50 Ω, 1 kΩ, and 10 kΩ) and an applied voltage of 2 V, showing the changes in Qe/CU0 and t1/2 with light intensity (L/L0), from which β/βL is derived. 2) devices at high light intensity as a function of resistance. c) Analysis of the TOF results as a function of excitation density, using the three different resistances (50 Ω, 1 kΩ, and 10 kΩ) and an applied voltage of 2 V, showing the changes in Qe/CU0 and t1/2 with light intensity (L/L0), from which β/βL is derived. | ||
The bimolecular recombination coefficient, β, of KP115:PCBM has been measured using TOF for KP115:PCBM solar cells. As previously reported, the photo-CELIV mobility of this system is μ = 1 × 10−4 cm2 V−1 s−1, with a corresponding Langevin recombination coefficient of βL = 6.0 × 10−11 cm3 s−1. The subsequent TOF experiments were performed as a function of circuit resistance, R,22 with 50 Ω, 1 kΩ and 10 kΩ investigated. The effect of altering the resistance is shown in Fig. 1b: the timescale over which the signal decays clearly increases with R. Due to the increase in circuit resistance, charge extraction from the device takes longer. The consequence of this is illustrated in Fig. 1c, which shows the changes in Qe/CU0 and t1/2 for each resistance as the light intensity is increased. The extracted charge Qe saturates at high excitation densities due to bimolecular recombination while t1/2 begins to increase when Qe = CU0, the charge stored on the electrodes (as shown by the dashed lines in Fig. 1c). Both observations have been seen in previous work on regioregular and/or annealed P3HT:PCBM, another non-Langevin system.9 As observed from Fig. 1b and 1c, the extraction time te (the difference in t1/2 at high and low excitation densities) increases significantly with increasing resistance. Furthermore, the quantity of charge extracted (relative to the capacitive charge) decreases with increasing resistance: the slower timescale of extraction allows more recombination to take place. The combination of these effects leads to an overall reduction in β/βL as the resistance is increased (Table 1); that is, the recombination behaviour appears to become even more strongly non-Langevin. At 10 kΩ, for example, the recombination coefficient is reduced by over two orders of magnitude compared to Langevin recombination, while at 50 Ω the reduction is a factor of 25. Experimentally, this decrease in β/βL with increasing resistance is attributed to a stronger increase in extraction time that is not fully compensated for by a proportional decrease in extracted charge. In turn this produces a β that decreases from 2.4 × 10−12 cm3 s−1 to 6.0 × 10−13 cm3 s−1 as the resistance is increased from 50 Ω to 10 kΩ. The possibilities are therefore that the β is decreasing as a function of time, t, or charge density, n.
| R (Ω) | t e (s) | Q e /CU0 | β/βL | β (cm3 s−1) |
|---|---|---|---|---|
| 50 | 2.3 × 10−6 | 7.7 | 0.04 | 2.4 × 10−12 |
| 1000 | 8.8 × 10−6 | 3.8 | 0.02 | 1.2 × 10−12 |
| 10000 | 3.9 × 10−5 | 1.9 | 0.01 | 6.0 × 10−13 |
Independently of the origin of the decreasing β, this result is important as it indicates that the extraction timescale (resistance) is a significant parameter for TOF that should be clearly defined. In order to investigate this more thoroughly, we have utilised a time-resolved charge extraction technique that provides information on the kinetics of charge density decay over time in the device active layer. As such, β can also be determined via this method. This charge extraction technique involves photogenerating charges with a nanosecond laser pulse in a photovoltaic device held at open circuit, followed by extraction of these charges under the built-in field by switching to short circuit after an adjustable delay time. This technique is similar to that employed by Shuttle et al.,23 except that the charge extraction technique performed here is accomplished as a function of delay time as well as light intensity. In this way we are able to establish if β decreases as a function of n (varying the light intensity) or t (varying the delay time).
The charge extraction results for KP115:PCBM solar cells are presented in Fig. 2. Integration of the extracted charge over time provides the charge density at each delay time (between the laser pulse and switch) measured. It is clear from Fig. 2 that KP115:PCBM exhibits biphasic recombination kinetics, with a fast excitation density-dependent phase from 200 ns to 20 μs and a slower power law phase until 1 ms. Such biphasic behaviour has previously been observed in TAS experiments on a number of different polymer/PCBM systems.24,25 The slow phase has typically been assigned to bimolecular recombination of dissociated charges in the presence of an exponential distribution of localised (trapped) states. Conversely, the fast phase, which is observed most clearly at high excitation densities, is usually assigned to bimolecular recombination of free charge carriers generated when the density of photogenerated charges exceeds the density of localised states. Furthermore, non-uniform charge distribution, such as charges located at the interfaces and/or contacts, may also influence these decay dynamics.
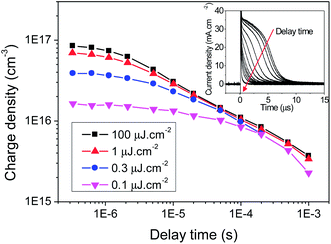 | ||
Fig. 2 Charge density decay with time as a function of laser excitation intensity (λexc = 532 nm) for KP115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCBM (1 PCBM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) photovoltaic devices, with an active layer thickness of 140 nm. Inset: the charge extraction curves as a function of delay time between the laser and the switch at one excitation intensity, the integration of which provides the charge density under those conditions. 2) photovoltaic devices, with an active layer thickness of 140 nm. Inset: the charge extraction curves as a function of delay time between the laser and the switch at one excitation intensity, the integration of which provides the charge density under those conditions. | ||
The kinetics of the fast phase can be fitted to a simple bimolecular equation:
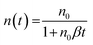 | (2) |
This slow phase, however, has previously been correlated with a time dependent bimolecular recombination coefficient in polymer:PCBM solar cells.17,26 This was therefore examined here for KP115:PCBM using an alternative method for obtaining β: by calculating the derivative dn/dt at each delay time, assuming pure bimolecular recombination:
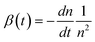 | (3) |
At early times (300 ns to 5 μs, see Fig. 3), the bimolecular recombination coefficient is independent of time, with a value of β ∼ 2.2 × 10−12 cm−3 s−1. This value is similar to that provided by the bimolecular equation fitting, as expected given that the same timescale was used, and also the TOF result at 50 Ω. At later times (from 5 μs), β shows a significant time dependence and decreases by an order of magnitude. This same behaviour in β as a function of time is observed irrespective of excitation density.
 | ||
Fig. 3 The bimolecular recombination coefficient β(t) of KP115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCBM (1 PCBM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) obtained from the charge extraction results at the highest excitation density using the derivative method (eqn 3), compared to the β values (and corresponding extraction times, marked with crosses) estimated from TOF at each resistance. 2) obtained from the charge extraction results at the highest excitation density using the derivative method (eqn 3), compared to the β values (and corresponding extraction times, marked with crosses) estimated from TOF at each resistance. | ||
These time-dependent β values estimated using charge extraction can now be compared to the resistance-dependent β values obtained using TOF; this is illustrated in Fig. 3. The observation of a resistance-dependent β is therefore a result of the timescale over which the charge is extracted in the TOF measurements, combined with biphasic bimolecular recombination decay kinetics that produces a time-dependent β. As the extraction timescale increases with R, more of the slow power law phase, which has a significantly – and increasingly – smaller β, is involved within that time period, thereby reducing the estimated β. In other words, the TOF provides an averaged β value for any given R, as it assumes only a single bimolecular recombination mechanism, rather than the more complex behaviour that is observed here. This averaged β value therefore includes both recombination phases, as has been previously noted for photo-CELIV measurements.27 This is an important result, implying that TOF may be limited in its ability to accurately describe bimolecular recombination in biphasic systems such as KP115:PCBM and, potentially, P3HT:PCBM.17 This is further illustrated in Fig. 4, which shows the simulated decay curves based on the single bimolecular recombination coefficients estimated using TOF. Not only do these curves fail to replicate the biphasic decay behaviour of KP115:PCBM, but the wider time range over which the single-mechanism recombination occurs is also evident for the higher resistances.
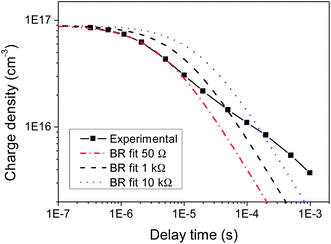 | ||
Fig. 4 Simulated bimolecular recombination (BR) curves using the β values estimated from TOF at each resistance, compared to the measured decay in charge density over time of KP115:PCBM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). 2). | ||
In conclusion, therefore, it has been observed that resistance is a vital parameter in TOF measurements that primarily affects the extraction time, giving a time-averaged bimolecular recombination coefficient. This has been exemplified by the KP115:PCBM system, which exhibits rare but highly desirable non-Langevin recombination behaviour. Furthermore, TOF may not be an appropriate technique to investigate the bimolecular recombination of polymer blend systems that exhibit biphasic decay dynamics and a time-dependent β. In this case, TOF should be used in conjunction with other charge extraction techniques to ensure a full description of the system in question is obtained.
Acknowledgements
The authors thank Russell Gaudiana and Andrew Nattestad for discussions, and Shogo Mori for providing the switch instrument. This research was supported under the Australian Research Council's Linkage and Discovery Projects funding scheme. AJM acknowledges the ARC for providing equipment support through LIEF, as well as supporting AJM and TMC with an Australian Research Fellowship and Australian Postdoctoral Fellowship Industry, respectively.Notes and references
- R. F. Service, Science, 2011, 332, 293 CrossRef CAS.
- M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Prog. Photovoltaics, 2011, 19, 565 Search PubMed.
- J. D. Servaites, M. A. Ratner and T. J. Marks, Energy Environ. Sci., 2011 10.1039/C1EE01663F.
- C. Deibel and V. Dyakonov, Rep. Prog. Phys., 2010, 73, 096401 CrossRef.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736 CrossRef CAS.
- C. G. Shuttle, B. O'Regan, A. M. Ballantyne, J. Nelson, D. D. C. Bradley and J. R. Durrant, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 113201 CrossRef.
- J. Peet, J. Y. Kim, N. E. Coates, W. L. Ma, D. Moses, A. J. Heeger and G. C. Bazan, Nat. Mater., 2007, 6, 497 CrossRef CAS.
- A. Pivrikas, G. Juška, A. J. Mozer, M. Scharber, K. Arlauskas, N. S. Sariciftci, H. Stubb and R. Österbacka, Phys. Rev. Lett., 2005, 94, 176806 CrossRef CAS.
- A. Pivrikas, N. S. Sariciftci, G. Juška and R. Österbacka, Progr. Photovolt.: Res. Appl., 2007, 15, 677 CrossRef CAS.
- R. Hamilton, C. G. Shuttle, B. O'Regan, T. C. Hammant, J. Nelson and J. R. Durrant, J. Phys. Chem. Lett., 2010, 1, 1432 CrossRef CAS.
- T. M. Clarke, A. M. Ballantyne, J. Nelson, D. D. C. Bradley and J. R. Durrant, Adv. Funct. Mater., 2008, 18, 4029 CrossRef CAS.
- W. W. Ma, C. Yang, X. Gong, K. Lee and A. J. Heeger, Adv. Funct. Mater., 2005, 15, 1617 CrossRef CAS.
- M. Reyes-Reyes, K. Kim and D. L. Carroll, Appl. Phys. Lett., 2005, 87, 083506 CrossRef.
- A. J. Mozer, N. S. Sariciftci, A. Pivrikas, R. Österbacka, G. Juška, L. Brassat and H. Bässler, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035214 CrossRef.
- I. Montanari, A. F. Nogueira, J. Nelson, J. R. Durrant, C. Winder, M. A. Loi, N. S. Sariciftci and C. Brabec, Appl. Phys. Lett., 2002, 81, 3001 CrossRef CAS.
- A. Pivrikas, G. Juška, R. Österbacka, M. Westerling, M. Viliunas, K. Arlauskas and H. Stubb, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 125205 CrossRef.
- T. M. Clarke, F. C. Jamieson and J. R. Durrant, J. Phys. Chem. C, 2009, 113, 20934 CAS.
- S. Subramaniyan, H. Xin, F. S. Kim, S. Shoaee, J. R. Durrant and S. A. Jenekhe, Adv. Energy Mater, 2011, 1, 854 CrossRef CAS.
- M. Zhang, X. Guo and Y. Li, Adv. Energy Mater, 2011, 1, 557 CrossRef CAS.
- J. Peet, L. Wen, P. Byrne, S. Rodman, K. Forberich, Y. Shao, N. Drolet, R. Gaudiana, G. Dennler and D. Waller, Appl. Phys. Lett., 2011, 98, 043301 CrossRef.
- T. M. Clarke, D. Rodovsky, A. A. Herzing, J. Peet, G. Dennler, D. DeLongchamp, C. Lungenschmied and A. J. Mozer., Adv. Energy Mater., 2011 DOI:10.1002/aenm.201100390.
- G. Juška, K. Genevičius, N. Nekrasas, G. Sliaužys and G. Dennler, Appl. Phys. Lett., 2008, 93, 143303 CrossRef.
- C. G. Shuttle, A. Maurano, R. Hamilton, B. O. Regan, J. C.d. Mello and J. R. Durrant, Appl. Phys. Lett., 2008, 93, 183501 CrossRef.
- H. Ohkita, S. Cook, Y. Astuti, W. Duffy, S. Tierney, W. Zhang, M. Heeney, I. McCulloch, J. Nelson, D. D. C. Bradley and J. R. Durrant, J. Am. Chem. Soc., 2008, 130, 3030 CrossRef CAS.
- T. M. Clarke, A. M. Ballantyne, S. Tierney, M. Heeney, W. Duffy, I. McCulloch, J. Nelson and J. R. Durrant, J. Phys. Chem. C, 2010, 114, 8068 CAS.
- M. P. Eng, P. R. F. Barnes and J. R. Durrant, J. Phys. Chem. Lett., 2010, 1, 3096 CrossRef CAS.
- J. Guo, H. Ohkita, S. Yokoya, H. Benten and S. Ito, J. Am. Chem. Soc., 2010, 132, 9631 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
