Perspectives on thermoelectrics: from fundamentals to device applications
M.
Zebarjadi
a,
K.
Esfarjani
a,
M. S.
Dresselhaus
b,
Z. F.
Ren
*c and
G.
Chen
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: gchen2@mit.edu
bDepartment of Physics and Department of Electrical Engineering and computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: millie@mit.edu
cDepartment of Physics, Boston College, Chestnut Hill, MA 02467, USA. E-mail: rench@bc.edu
First published on 23rd November 2011
Abstract
This review is an update of a previous review (A. J. Minnich, et al., Energy Environ. Sci., 2009, 2, 466) published two years ago by some of the co-authors, focusing on progress made in thermoelectrics over the past two years on charge and heat carrier transport, strategies to improve the thermoelectric figure of merit, with new discussions on device physics and applications, and assessing challenges on these topics. Understanding of phonon transport in bulk materials has advanced significantly as the first-principles calculations are applied to thermoelectric materials, and experimental tools are being developed. Some new strategies have been developed to improve electron transport in thermoelectric materials. Fundamental questions on phonon and electron transport across interfaces and in thermoelectric materials remain. With thermoelectric materials reaching high ZT values well above one, the field is ready to take a step forward and go beyond the materials' figure of merit. Developing device contacts and module fabrication techniques, developing a platform for efficiency measurements, and identifying applications are becoming increasingly important for the future of thermoelectrics.
 M. Zebarjadi | Mona Zebarjadi is a postdoctoral associate in the Department of Mechanical Engineering at Massachusetts Institute of Technology, working jointly with Prof. Dresselhaus and Chen. She obtained her PhD in electrical engineering from the University of California, Santa Cruz in November 2009 working with Prof. Ali Shakouri. Prior to UCSC, she received her BS and MS in physics from Sharif University of Technology, Iran in 2002 and 2004, respectively. Her current research is on charge and heat transport in semiconductor-based devices and nanoscale energy conversion devices with a focus on thermoelectrics. |
 K. Esfarjani | Keivan Esfarjani obtained his PhD in condensed matter theory from the University of Delaware in 1991. He was an assistant and then an associate professor at the Institute for Materials Research of the Tohoku University from 1993 to 2001. He was then an associate professor at Sharif University of Technology, visiting associate professor at the University of California in Santa Cruz, and is presently research scientist at the Massachusetts Institute of Technology. His research interests are in electronic structure calculations, and charge and heat transport in low-dimensional materials, especially carbon nanotubes. |
 M.S. Dresselhaus | Mildred Dresselhaus is an Institute Professor of Electrical Engineering and Physics at MIT. She is the recipient of the National Medal of Science and 28 honorary degrees worldwide. She has served as President of the American Association for the Advancement of Science, Treasurer of the National Academy of Sciences, President of the American Physical Society, and Chair of the Governing Board of the American Institute of Physics. She served as Director of the Office of Science at the U.S. Department of Energy. Professor Dresselhaus's research over the years has covered many topics in Condensed Matter Physics and energy-related topics. |
 Z.F. Ren | Dr Zhifeng Ren, a professor of physics at Boston College, specializes in thermoelectric materials, solar thermoelectric devices & systems, photovoltaic materials & systems, carbon nanotubes & semiconducting nanostructures, nanocomposites, bioagent delivery & biosensors, and superconductors. He is a fellow of APS and AAAs, a recipient of R&D 100 award, has published extensively, and was ranked as the 49th of the top Materials Scientists worldwide. He has co-founded three companies in the field of carbon nanotubes, thermoelectric materials, and photovoltaics. |
 G. Chen | Dr Gang Chen is currently the Carl Richard Soderberg Professor of Power Engineering at Massachusetts Institute of Technology. He obtained his PhD degree from UC Berkeley in 1993 working under then Chancellor Chang-Lin Tien, master and bachelor degrees from Huazhong University of Science and Technology, China. He was a faculty member at Duke University (1993–1997), University of California at Los Angeles (1997–2001), before joining MIT in 2001. He is a recipient of the NSF Young Investigator Award, the ASME Heat Transfer Memorial Award, and the R&D 100 Award. He is a member of the US National Academy of Engineering, a Guggenheim Fellow, an AAAS Fellow, and an ASME Fellow. He has published extensively in the area of nanoscale energy transport and conversion and nanoscale heat transfer. He is the director of Solid-State Solar-Thermal Energy Conversion Center funded by the US DOE's Energy Frontier Research Centers program. |
Broader contextThermoelectric power generators are solid state devices which can directly convert heat into electricity. Despite their clean and environmentally friendly operation, their current commercial applications are limited because of their low efficiency. A thermoelectric power generator device consists of heavily doped semiconductor legs which are connected electrically in series and thermally in parallel. Fundamental understanding of heat and charge carrier transport inside the thermoelectric legs can lead to new strategies to design and fabricate high efficiency thermoelectric materials. The device efficiency not only depends on materials, but also on an optimum choice of the legs' size, configuration, and contacts. Finding new applications for thermoelectric devices in places that they are superior to other technologies is another challenge for the thermoelectric community. This review article focuses on recent advances in the thermoelectric field from fundamental studies of charge and heat carrier transport to the final device fabrication and applications. |
Introduction
The direct energy conversion between heat and electricity based on thermoelectric effects without moving parts is attractive for many applications in power generation and heat pumping. The efficiency of the thermoelectric energy conversion is an increasing function of the materials' nondimensional figure of merit, ZT = σS2T/κ, where σ is the electrical conductivity, S the Seebeck coefficient, T the temperature and κ the thermal conductivity. For a long time, the best known thermoelectric materials were bismuth telluride-based alloys2 with a ZT around 1. Since the 1990s, there has been a renewed interest in thermoelectric technology, stimulated by ideas in using low-dimensional structures, new bulk materials, and increased government funding.3 Significant advances have recently been made in increasing ZT.There have been many excellent recent reviews to cover different aspects of the thermoelectric field, including a global view of thermoelectrics, their place and potential among other renewable energies,4 advances in different classes of thermoelectric materials,5 nanostructured thermoelectric materials,6–8 semiconductor nanowires,9 interfaces in bulk thermoelectrics10 and energy dissipation in nanoscale devices.11 In 2009, we published a review on bulk nanostructured thermoelectric materials, current research and future advances.1 Rather than being a comprehensive review, the article emphasized challenges in understanding carrier transport in bulk and nanostructured materials, and reviewed the research that has been done in addressing those challenges. Questions for which we do not have a clear answer, such as which carriers are the dominant heat/charge carriers in nanocomposites, what is the optimal size distribution of nanostructures, what type of interfaces lead to the strongest phonon scattering and the weakest electron scattering, were mainly discussed. Validity of the Boltzmann transport equation was questioned for use in nanostructures where the mean free path can become shorter than the wavelength. Finally, strategies which could lead to the next generation of bulk nanostructured TE materials were identified.
Since the time of our last review,1 more than 3000 journal papers were published in the field of thermoelectrics. New materials, strategies, fabrication techniques and new applications have been proposed and are being studied. The thermoelectrics field keeps expanding and significant progress continues to advance more quickly in both materials and fundamental understanding. At the same time, many new questions have been raised and many old questions remain to be answered. In the present review, we primarily report on some advances made in the past two years in the thermoelectric field. Similar to the previous review, we choose to focus on challenges of the field rather than a comprehensive literature review, and we present many viewpoints derived from our own research. We skip giving an introduction to thermoelectric materials and we refer our readers to existing reviews in the field to understand the basic physics behind thermoelectric energy conversion. In addition, in the current review, we extend our view from a materials perspective to include a device perspective. In addition to sections on theoretical and experimental advances in material design, we add more sections to address device design, performance, cost and new application areas such as to solar thermal.
The review is organized as follows: in the first part of the review, we update the advances in studying carrier transport in thermoelectric materials. In the second part, we give an update of new strategies for designing high-efficiency and low-cost thermoelectric materials. We then discuss the challenges and advances in making a commercial thermoelectric generator (TEG) device. Finally, we discuss new applications of TE devices, especially solar thermoelectric power generators (STEGs).
I. Advances in carrier transport
A. Phonon transport
A successful strategy in enhancing ZT is through reducing the phonon thermal conductivity using nanostructures. Studying phonon transport in nanocomposites requires knowledge of phonon transport in bulk materials in addition to phonon transport across interfaces. As pointed out before,1 even in bulk materials, there is much uncertainty regarding the values of key quantities such as the phonon mean free paths (MFPs). While simplified models such as the Callaway model12 are able to fit the experimental results by adjusting different parameters, they cannot predict the phonon mean free path distribution correctly. Nanocomposites add another layer of complexity as they introduce many interfaces. The structure of these interfaces, the phonon transmissivity at a single interface and multiple scattering events associated with the interfaces when the spacing is closer than the phonon MFP are not well understood.We developed a simpler lattice dynamics model than the more precise approach of Broido et al.13 Using harmonic and anharmonic force constants extracted from DFT calculations within a supercell,20 a force field is built in powers of atomic displacements about the equilibrium positions. From this force field, we can compute the bulk thermal conductivity using two different approaches:
(1) Equilibrium molecular dynamics methods use the Green–Kubo21,22 formula, which relates the thermal conductivity to the time integral of the equilibrium heat current autocorrelation. Typically, a molecular dynamics simulation is performed in a large supercell. After reaching thermal equilibrium, data on the heat current are collected over a long time period on the order of nanoseconds. The autocorrelation of these data, when integrated over time and ensemble-averaged, will provide the thermal conductivity at that temperature. The major shortcoming of the classical molecular dynamics method has been the lack of a reliable inter-atomic potential. Empirical potentials lead to errors typically on the order of 50% or more, although they can be useful in predicting trends. Two noticeable improvements in this area are the use of the ab initio molecular dynamics simulations as described in the work of Koker,17 and the development of a Taylor expansion (polynomial) potential which is accurate but only valid for small displacements.20 The equilibrium molecular dynamics approach has the advantage of being valid at high temperatures. It can also be used to investigate the effect of alloying and substitutional disorder without much extra work.23 It suffers, however, from uncertainties due to the statistical treatment of the molecular dynamics (MD) data. Often, MD simulations provide only one number, namely κ(T) at a given temperature, although interesting information, such as the phonon mean free path, can be extracted.24,25
(2) The alternative approach is the use of lattice dynamics (LD) theory, which uses harmonic force constants to calculate phonon dispersions and group velocities. Using perturbation theory, phonon life times can be calculated from the anharmonic force constants, and the thermal conductivity is obtained by using the relaxation time approximation. Phonon scattering mechanisms due to impurities, system or grain boundaries and three-phonon processes can all be included by adding their scattering rates in order to obtain the total relaxation time. This quantum mechanical approach, which is accurate at low temperatures, gives access to the distribution of MFPs and their relative contribution to κ, but can lose accuracy when the perturbation is large, such as at high temperatures or for highly disordered materials and structures. We have successfully applied this formalism to the cases of silicon,26lead telluride,27gallium arsenide28 and half-heuslers.23 The calculated results of the thermal conductivity versus temperature as compared to experiments are shown in Fig. 1. The cumulative thermal conductivity29versus mean free path for each material is shown in Fig. 2. Such studies are helpful to accurately determine the phonon mean free paths in different crystals, find out which phonons are carrying most of the heat, and accordingly to then design nanostructures of proper size. For instance from Fig. 2 it can be inferred that nanostructures of 10–100 nm size can efficiently reduce the thermal conductivity of Si, while for PbTe, smaller inhomogeneities and alloying might be more effective in reducing κ.
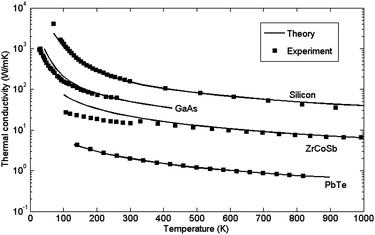 | ||
| Fig. 1 Thermal conductivity of different bulk crystalline materials calculated from first-principles lattice dynamics in our group in comparison with the relevant experimental measurements. Silicon: ref. 26, GaAs: ref. 28, ZrCoSb: ref. 23 and PbTe: ref. 27. | ||
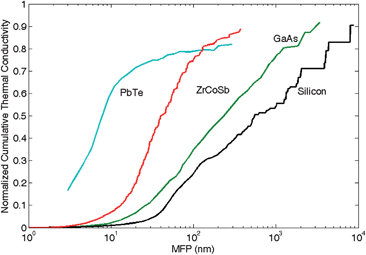 | ||
| Fig. 2 Normalized cumulative thermal conductivity at room temperature versus mean free path calculated from first-principles. | ||
The experimental determination of phonon mean free path is even more challenging, but there are some encouraging developments. Although limited to single crystalline materials, inelastic neutron scattering should be able to provide precise information on phonon lifetimes.30 In addition, some optical methods are emerging as promising tools to probe phonon mean free path in common laboratories. Cahill probed different parts of the phonon distribution by using a variable frequency time-domain thermoreflectance method.31 The idea is that when phonons have a mean free path longer than the thermal diffusion length as determined by the thermal diffusivity and the modulation frequency, their contributions to heat conduction are overpredicted and one should measure a smaller thermal conductivity, as observed in some alloys samples studied by the Cahill group. Minnich et al.32 developed a thermal conductivity spectroscopy method based on pump–probe experiments to measure the mean free path over a wide range of length scales. This new method is based on the prediction that the heat flux from a heat source will be lower than that predicted by Fourier's law when some phonon mean free paths are longer than the heater dimensions due to nonlocal heat conduction external to the heat source.33 This prediction was recently confirmed experimentally using a soft X-ray transient grating technique. In that work, an additional ballistic thermal resistance was observed when measuring the resistance of heat dissipation from a nanoscale heat source into the bulk.34 Minnich et al. observed a heat source size dependence in the measured thermal conductivity of Si and found that by systematically changing the laser beam size, contributions of phonons with different mean free paths to the thermal conductivity can be mapped out. The results for silicon are in agreement with the first-principles calculations.32 The authors further advanced the technique to allow mapping of the thermal conductivity over a wide range of length scales.35,36 The development of these sorts of tools will provide valuable information to understand phonon transport in more detail. At this stage, these tools are not routine and need to be developed and applied to a wide range of materials. A database of the experimentally measured and the theoretically calculated mean free path distributions for different thermoelectric materials would be of significant use for the thermoelectrics community.
For predicting thermal properties, not only is the knowledge of TBR required, but also more importantly, a knowledge of the interface transmission and reflection (frequency and mode dependence of carrier transport) is needed. There is not a well-developed appropriate tool yet available either experimentally or theoretically for studying interface transmission.
Existing experiments include picosecond (nowadays extended to femtosecond) reflectance thermometry and scanning optical thermometry (or micro-device optical thermometry).37 Reflectance thermometry involves splitting the laser output into two beam paths, a “pump” beam and a “probe” beam, and adjusting the relative optical path lengths with a mechanical delay stage.37 This technique offers nanometer-size resolution. However, this technique is more appropriate for studying metal–semiconductor interfaces than interfaces in nanocomposite materials. Moreover, experimental data for the thermal decay at short times t < 50 ps are difficult to interpret quantitatively because of hot-electron effects which can deposit energy outside of the optical absorption depth, the unknown temperature dependence of the complex index of refraction, the failure of the diffusion equation for small length scales and the nonequilibrium between phonons and electrons in this regime.37 Optical thermometry is also more appropriate for metal–semiconductor interface studies and its resolution is limited by the diffraction limit (near 1 μm).
On the theory side, several old models exist. The first one is the acoustic mismatch model (AMM)38 which is based on the assumption of specular scattering at the interfaces. Specular scattering means that the wave vector direction follows the Snell–Descartes' law of reflection and refraction. The AMM works for ideal interfaces at low temperatures (T < 7 K) because most phonons have long wavelengths and AMM is appropriate for treating them. The other model is the diffusive mismatch model (DMM),39 which assumes that the scattering at the interface is elastic but the incoming phonon momentum memory is completely lost and therefore the outgoing wave vector direction is random. A further restrictive condition of the DMM model is that the phonon reflectance is set equal to the transmittance based on the argument that the reflected and transmitted phonons cannot be distinguished. Clearly, this is a gross approximation and therefore the DMM is not a predictive model at all.
The thermal boundary resistance is a highly nonequilibrium concept, and standard expressions used for the thermal boundary resistance are based on the temperatures of the incoming phonons, contrary to the temperature definitions used in typical pump–probe experiments. Consistent expressions40,41 for the thermal boundary resistance should be used when comparing experiments and modeling, a practice which is clearly not followed in the prevailing literature.
Due to the limitations of existing models, efforts are now mostly based on numerical methods including molecular dynamics42–45 and the Green's function approach.46,47
The non-equilibrium molecular dynamics (NEMD) model simulates directly the temperature drop across an interface using molecular dynamics by imposing a temperature difference between two reservoirs at the two sides of the interface. Its main drawbacks include: (1) the thermal boundary resistance values depend on the size of the simulation domain and (2) it does not give the phonon transmission but only calculates the contribution of phonons to the TBR. The size dependence arises from the fact that phonons reaching the interface can be ballistically generated in the reservoirs, which are usually thermalized randomly and are not following similar scattering processes as in bulk materials. Sellan et al.48 studied the size dependence of the NEMD results. The size dependence is basically due to artificial scattering processes occurring at the supercell boundaries. Even though equilibrium MD methods converge relatively quickly with size, NEMD results need to be properly extrapolated to infinite size by performing several simulations with supercells of various lengths for convergence. For predicting the thermal conductivity of nanocomposites using the Boltzmann equation or a Monte Carlo simulation,49–51 phonon transmission/reflection information at an interface is most useful, but it is difficult to extract such information from a NEMD simulation.
More exact methods such as those based on Green's function formalism are able to calculate the transmission coefficient. With force constants obtained from first-principles calculations, the thermal boundary resistance of the metal–graphene nanoribbon interface52 and the graphene–quantum dots interface53 was recently calculated. The Green's function method is exact within the harmonic approximation or at low temperatures where anharmonicity is small. Therefore, it is more suitable for interfaces in which randomness (e.g., surface disorder, mass disorder, etc.) is a dominant effect and the anharmonicity is negligible. An extension of the Green's function method to the anharmonic case has been developed and discussed in detail by Mingo54,55 and Wang et al.,56 but it has not yet been applied to realistic materials.
In the case of metal–semiconductor (or insulator) interfaces, the electron–phonon interaction also needs to be considered.57 Majumdar and Reddy58 have shown that this adds a resistance in series to that due to phonon transmission. Mahan59 recently developed a theory to calculate the thermal resistance at a metal and a polar insulator interface. He proposed that electrons and phonons are linked at the interface by the image charges from the vibrating atoms of the polar material. They would interact through the electrons' screening cloud, with their image charges located in the metal, and therefore exchange energy with them, causing an interfacial thermal resistance.
Another instance where the interfacial thermal resistance becomes an important factor is in superlattices. There the cross-plane thermal conductivity shows a minimum with respect to the superlattice period60–62 while its in-plane component usually increases with the period. The increase in thermal conductivity with increasing periodic thickness is understood to be due to interface roughness scattering,63 while the decrease in thermal conductivity at low period thickness limit is mainly due to phonon tunneling.
Despite these advances, the interface transmission/reflection is still not well understood at this stage and more research needs to be done to give a clear answer to questions like what is the effect of anharmonicity and electron–phonon coupling on interfacial thermal transport. Indeed anharmonicity is largest at the interface because even if both sides of the interface are harmonic, atoms at the interface will feel an uneven (anharmonic) potential because of the different materials involved. The importance of this fact has not been elucidated yet.
B. Electron transport
Electron transport has all the complications of phonon transport. In addition to studying the electrical conductivity, one needs to study the Seebeck coefficient to optimize the thermoelectric power factor.The exact derivation of the Seebeck coefficient comes from using the continuity equations to pass from carrier densities to current operators and the formalism has been derived by Onsager64 and Kubo.22 The formalism in the single electron picture can be simplified to express the Seebeck coefficient in terms of transport coefficient integrals.65 From this formalism, the widely used Mott formula, which expresses the Seebeck coefficient as the logarithmic derivative of the differential conductivity with respect to the chemical potential, can be easily derived. Recently Peterson and Shastry66 proposed a new framework to calculate the Seebeck coefficient. Based on their derived formula, the Seebeck coefficient is given as the particle number derivative of the entropy at constant volume and temperature (∂S/∂N)T,V. This formula has the advantage of being valid beyond the one-electron approximation, and can be applied to strongly interacting systems.
Just like the case of the thermal conductivity, the electrical conductivity and the Seebeck coefficient can be fitted to reproduce the temperature dependent experimental data. Fits of the Seebeck coefficient usually determine the Fermi level, and then the relaxation times can be fitted based on the electrical conductivity or carrier mobility. Since many models can be used to fit the same set of data, their reliability is always questionable unless these models can predict other properties which were not used in the fitting process. As already mentioned, for phonon transport in bulk structures, first-principles calculations which are free of fitting parameters have helped the field progress in the past few years. For the case of electrons, these methods are still far from complete.
More sophisticated methods have been proposed and successfully used to predict accurate electronic bands. In order of complexity, they go from screened exchange,68 hybrid screened Coulomb,69LDA + U,70 and DMFT71 to GW72 and the Bethe–Salpeter (BS) equation,73 as described below.
The Hartree–Fock theory, which includes electrostatic Coulomb and exchange interactions, largely overpredicts the band gap due to the lack of screening. Bylander and Kleinman introduced a screened exchange potential68 which alleviates this shortcoming and improves the band gap. The LDA, on the other hand, uses an exchange-correlation potential which is fitted to that of the interacting uniform electron gas (jellium) which is a metal. Therefore the LDA is more accurate for metals where the electron density is more or less uniform. Insulators and semiconductors have a strongly inhomogeneous electron density, but the LDA functional tends to make them “more metallic”, and thus produces a smaller bandgap. Hybrid functionals attempt to partially include exchange effects. A recent version that has successfully been used and produced accurate band gaps for semiconductors is the so-called HSE69 functional. The LDA + U method introduces an onsite Coulomb repulsion represented by U. It is found that LDA + U increases the gap in systems such as oxides, where Coulomb interactions are important.74,75 The more sophisticated dynamical mean-field theory (DMFT)71 does the same but includes dynamical effects in the Coulomb correlations. It has been successfully applied to compounds which include transition metals with 3d states or rare earths with strongly localized 4f states in which Coulomb interactions are dominant.76 The more complicated GW method is based on the Green's function formalism and incorporates dynamical effects, nonlocality and screening within various approximations. It has accurately reproduced the bandgap of most sp semiconductor compounds for which collective modes play a more important role than onsite Coulomb interactions. Finally the BS equation has been used to accurately calculate the optical properties of molecules and semiconductors.
To summarize, increasingly complex methods based on DFT have been developed to address the bandgap issue, therefore allowing a more accurate prediction of the Seebeck coefficient and the bipolar effect. It must be emphasized that DFT is a ground state theory. As such, it is supposed to give the correct ground state energy and electron density only. As a result, all quantities which can be obtained from changes in the total energy, such as forces, force constants, chemical potential and hardness, magnetization and susceptibility, etc., are supposed to be accurately and reliably calculated by DFT. Unoccupied states are not supposed to be correctly calculated by the DFT. Many-body methods such as GW provide systematic improvements, which are developed specifically to accurately calculate electronic excitations of semiconductors.
In practice, first-principles calculations can be performed only on limited supercell sizes. Therefore, it is difficult to include long-range potentials such as ionized impurity scattering effects in these calculations. Recently Restrepo et al.84 calculated the ionized impurity rate from first-principles, but they had to assume a screened tail for their potential. They calculated the mobility of silicon within the relaxation time approximation (RTA) including electron–phonon and ionized-impurity scattering mechanisms calculated from first-principles and combined with a band structure obtained from DFT. Wang et al.85 extended this formalism and calculated the mobility of silicon beyond the RTA. They included several scattering rates, from which only the electron–phonon scattering rate was derived from first-principles.
The next problem is that inelastic scattering mechanisms such as electron–phonon scattering play an important role in determining the electron mobility in thermoelectric materials. In the presence of inelastic scattering, the RTA is not valid. Therefore, at elevated temperatures where most of the thermoelectrics work is done, the RTA is not applicable. But due to its simplicity it has been widely used in the field of thermoelectrics. Other more complex approaches such as Sondheimer's variational method,86 Rode's iterative method87 or Monte Carlo technique should be used to correctly deal with the inelastic electron–phonon scattering.
Despite the fact that the Monte Carlo technique is widely used for the case of electron transport in semiconductors, it has not been used as often in the thermoelectric field. The main reason is that this method is very costly and is more suitable for low doping concentrations and high applied electric fields, whereas thermoelectrics usually operate under high doping concentrations and low applied electric fields. Still, the Monte Carlo technique is a useful tool to study heat dissipation at submicron scales,88,89 interface roughness90 and nonlinear thermoelectric effects.91 It should be noted that the Monte Carlo technique goes beyond the RTA but it requires scattering rates as input.
Much like the case of phonons, nanostructure interfaces introduce an important scattering mechanism for thermoelectric materials. Here we focus on only two types of nanostructures: first, nanoparticles embedded in a host matrix, and second, a heterostructure geometry with nanoparticles adjacent to each other.3 In such geometries it is important to understand the relative size scales. If nanoparticle sizes are smaller than the electron MFP and their average separation is much larger than the electron MFP, they could be considered as scattering centers and the leakage of the electron wave function inside the nanoparticles could be ignored. In this picture, electrons are travelling in accordance with the dispersion relations of the host matrix and the nanoparticles only add another term to the scattering relaxation times.92–95 Now the only complexity is to calculate the electron–nanoparticle scattering cross-section. This can be calculated using either the Born approximation for weak potentials or partial wave technique (average T-matrix method) for strong nanoparticle potentials.96,97 However, the main problem is that the nanoparticle potential is not known experimentally and most commonly its height is used as a fitting parameter. This creates some uncertainty about the effect of the nanoparticles on the TE transport.
If the distance between nanoparticles is smaller than the electron MFP, then multiple scattering events become important.98 If nanoparticle sizes are much bigger than the electron MFP, the electron wave function leakage into the nanoparticles is not negligible. In this case, conduction electrons spend a considerable amount of time inside the nanoparticles and experience multiple scattering events before they leave the nanoparticle and this process destroys the coherent transport picture. Currently, such cases are not well understood and there is a need to study the incoherent scattering from nanoparticles.
Once the electron MFP becomes comparable or smaller than the electron wavelength, the validity of the BTE becomes questionable and more powerful tools such as non-equilibrium Green's functions which explicitly take account of electron wave effects and coherency are required.99 Wang and Mingo100 used the Green's function method to simulate rough surfaces and showed that such surfaces do not lead to an enhanced power factor as was previously suggested.101
At this point, our understanding of electron transport is not as well developed as our understanding of phonon transport, even though both are based on DFT. The extension of transport theory, from bulk to nanostructures, is still under development. Nanostructures, with their many interfaces, impose big challenges since the potential at the interfaces is not known, and the electron transmission/reflection from the interfaces, especially in the presence of other scattering mechanisms, has not yet been well studied.102 One of the problems is the fact that TE materials usually have complex compositions and structures. To these complex structures, usually several external elements are added to improve either the thermoelectric or mechanical properties or both. The final fabricated thermoelectric sample is thus usually a complex nanocomposite for which we do not know the band alignment between the different phases and local electronic structures. The electronics community can contribute to this field through advancing our understanding of charge transport in complex nanostructured materials.
There is a great need for studying electron transport in more detail. The next generation of thermoelectric materials requires more attention to be given to enhancement of the electronic properties since the lattice thermal conductivity of the thermoelectric materials has already been greatly reduced.
II. Strategies for the next generation of nanocomposites
In our previous review, we dedicated a section on strategies to improve the performance of nanocomposites. In this section we would like to first summarize some of the previously discussed strategies, update their current status and then introduce a few additional strategies that have been proposed in the past two years. Some of these are not really new but only have been recently demonstrated experimentally.Fig. 3 shows some of the important ZT enhancements which have been reported in the literature and several of them are recent. We need to point out that in the TE field, there have been many false or irreproducible data reported in the past. Furthermore, some published papers do not fully disclose their measurement techniques and therefore can be difficult to reproduce or check. What we are lacking in the field is mainly a standard characterization technique. For example, in the field of photovoltaics, NREL plays an important role and every advanced photocell is sent to them for proof of its high efficiency. The existence of such a unique center would also be beneficial to the thermoelectric field by providing a fair comparison between different materials. On this front, ORNL has a center. In one recent round-robin study led by ORNL,103 it was found that specific heat measurements have largest uncertainty. The specific heat values are needed in calculating thermal conductivity from the measured thermal diffusivity based on the popular laser flash method. This fact highlights why many reported ZT values cannot be reproduced by others. The methodology used to characterize the three parameters determining ZT is inherently more difficult than the photovoltaic efficiency measurements. The thermoelectrics community could benefit from more efficiency measurements104,105 and a platform for thermoelectric efficiency measurements should be standardized.
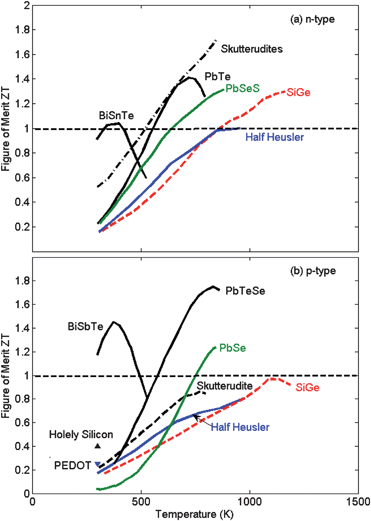 | ||
| Fig. 3 Some of the important ZT values reported in the literature for (a) n-type and (b) p-type samples: n-type BiSeTe, ref. 106; n-type SiGe, ref. 107; n-type PbTe, ref. 108; n-type PbSeS, ref. 109; n-type skutterudites, ref. 110; n-type half-Heuslers, ref. 111; p-type BiSbTe, ref. 112; p-type SiGe, ref. 113; p-type PbTe, ref. 126; p-type PbSe, ref. 114; p-type Skutterudites, ref. 115; p-type half-Heuslers, ref. 116; Holely Silicon, ref. 134 and PEDOT, ref. 139. | ||
One of the strategies that has been discussed before was energy filtering at the interfaces.117–119 In the energy-filtering approach, energy barriers are used to block the low-energy electrons and therefore, increase the average heat transported per carrier. By definition, then the Seebeck coefficient increases and could result in an enhanced power factor. The concept of energy filtering has been extensively studied by Shakouri and co-workers.118,120 The same interfaces can also substantially reduce the carrier mobility and therefore, such an approach requires careful design of the nanostructures in order to produce an optimum power factor. This approach was originally proposed for superlattices where alternate energy barrier layers could act as energy filters. These days, it has been extended to three-dimensional bulk materials, where either nanoparticles or grain boundary interfaces play the role of an energy filter. It was predicted that nanoparticles will not be able to be an effective filter in 3D, because even low-energy electron wave functions can go around the nanoparticle. It is possible that a high concentration of nanoparticles can localize low-energy electrons and create a mobility edge.121 Only in this case can the term energy filtering be used. Grain boundary interfaces are probably more effective energy filters if their barrier height is relatively uniform all around the grain. At this point it is not clear whether this condition is satisfied by the “walls” of surrounding grains.
In general, it is hard to prove that energy filtering takes place in a device because it requires knowledge of the energy dependence of the scattering rates. The latter cannot be directly extracted from experiments. There are several recently reported claims of observing energy-filtering effects but these claims are limited to only small enhancements in the power factors. The main evidence for observing energy filtering is the observation of an enhanced Seebeck coefficient compared to that of the host matrix.122,123 It should be noted that the relaxation times τ change when nanostructures are added, and as a result the Seebeck coefficient of the nanostructures is not directly comparable to that of the host matrix. The Seebeck coefficient is the ratio of the slope of the differential conductivity versus energy to its absolute value at the Fermi level. The enhancement of the Seebeck coefficient could only be a result of the reduced differential conductivity (electrical conductivity) as a result of introducing additional scattering centers in the nanostructure case, but this is not energy filtering.
In a few kBT window around the Fermi energy, the total relaxation rate, 1/τ(E), can have several possible behaviors, as shown in Fig. 4. The energy dependence of the relaxation times in the simplest form can be described as τ = τ0Er, where the exponent r is called the scattering parameter, for example, in the case of acoustic phonon scattering τ ∝ E−1/2 and in the case of weak impurity scattering τ ∝ E3/2. An increase of the scattering parameter results in an increase in the slope of the differential conductivity and therefore also in the Seebeck coefficient. Evidence for such an increase provides a convincing proof of the filtering effect. Heremans et al.124 developed a four coefficients measurement protocol in which four transport properties are measured: resistivity, Seebeck coefficient, Hall coefficient and Nernst coefficient. Then four characterization parameters are identified from these measurements: effective mass, mobility, Fermi level and the scattering parameter. Using this protocol they have observed that nanogranular PbTe samples exhibit higher scattering parameters compared to their bulk counterpart. Even though this method provides more solid evidence, it is still not considered to be a good proof of electron filtering. While filtering means that there is a sharp cut-off in the scattering rates at energies close to the barrier height (see Fig. 4c), increase of the scattering parameter is only evidence of the fact that low energy electrons are scattered more strongly than high energy electrons and does not imply a sharp cut-off. Observation of such sharp cut-offs may be more possible in one-dimensional transport processes rather than for 3-dimensional transport.
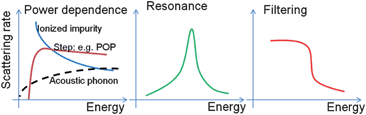 | ||
| Fig. 4 (a) The scattering rates 1/τ versus energy E can have a step as a function of energy in the case of polar optical phonon (POP) emission (left-solid brown), 1/τ can change according to different powers of energy as discussed in the text. (b) 1/τ can have a spike in the case of resonant scattering (center), or finally (c) 1/τ can have a sudden drop (right), which we can define as “energy filtering” since the scattering is weak for energies higher than the energy drop, and 1/τ is strong for lower energies. The last two cases will cause sharp features in the differential conductivity. This in turn will lead to a large Seebeck coefficient. | ||
The other discussed strategy was the introduction of resonant impurity levels inside the conduction or valence band. Such resonant states create sharp features in the density of states and therefore are expected to enhance the Seebeck coefficient. An experimental demonstration of the concept of the resonant density of electronic states was made by Heremans and co-workers125 in bulk Tl-doped PbTe. The explanation of the experiment at the time was based on the discussion that the Tl atoms strongly hybridize with the lattice, changing the density of states and creating resonance impurity levels inside the valence band. It has been shown recently that other dopants in PbTe could also lead to very high ZT values and that the high ZT is related to the highly degenerate band structure of PbTe.126 We will discuss this new perspective in part C. Despite this argument, it is still reasonable to think that introducing resonant levels can improve the thermoelectric efficiency of a material. Identifying what kind of dopants can introduce resonant states in a particular host material holds the key.
We have also discussed strategies to enhance the mobility, and this has been achieved via different approaches recently. We will discuss this work in detail in part B, in the context of modulation doping.
A. Nanoparticles in the alloy approach
Probably the simplest strategy to enhance ZT is to introduce nanoscale structures which scatter phonons more efficiently than electrons. A large atomic mass mismatch can be used to scatter phonons effectively. At the same time a similar work function and a small band offset are required to scatter electrons as weakly as possible. The theoretical challenge for a given host matrix is to find a proper nanoparticle material which satisfies the above criteria. However, the bigger challenge in practice is to embed the desired nanoparticle with the proper size inside the host matrix without introducing second phase formation.Within the Born approximation (weak potentials), the scattering cross-section (σ) for low energy electrons off of a single nanoparticle is σ(ka ≪ 1) = 16πm2V2a6/9ħ4, and for high energies the scattering cross-section decreases as inverse of energy, σ(ka ≫ 1) = πmV2a4/ħ2E. In this notation, m, E and k are the electron effective mass, energy and wave vector, respectively, while V and a are the potential energy and radius of the nanoparticle, respectively. The cross-section σ has a strong dependence on the potential radius in both the high and low energy limits.127 If there is a charge transfer between the nanoparticle and the host matrix, due to a long range Coulomb potential, the effective potential radius is much larger than the nanoparticle radius itself and as a result, cross-section increases significantly. Therefore, such charge transfers should be prevented as much as possible. This is in contrast to the modulation-doping approach as we will see later on. For this reason, one should choose materials with the same work functions to prevent charge transfer. Unfortunately, as pointed out before, there is a lack of information in terms of knowing about the work functions of most of the TE materials. This makes the choice of the proper nanoparticle even more difficult. Once a nanoparticle with a similar work function has been chosen, the band offset between the two materials determines the strength of the potential (V). Barrier potentials scatter electrons less than well potentials.97 The scattering cross-section off a step-barrier potential at high energies is limited by twice that of the geometrical limit to 2πa2 (due to interference, an electron scatters once from the particle and once from its shadow).127 At low energies the scattering cross-sections are limited to 4πa2. This term should be compared with other electron scattering cross-sections, such as with phonons, impurities and alloy scattering and ideally it should be negligible compared to them. Similarly, the phonon scattering cross-section off of a single nanoparticle at low energies is determined by σ(qa ≪ 1) = 4π(ΔM/M)2q4a6/9 and at high energies σ is limited by the geometrical optics limit.128
Note that since the potential that the electrons experience is the band offset while the potential that the phonons experience is related to the atomic mass ratio between the nanoparticle and the host material, it is possible to find nanoparticles which affect one type of carrier more than the other. Even if we are in the geometrical optics limit for both electrons and phonons (i.e., if they both see the same cross-section), it is possible to find limits in which phonons are scattered effectively while electrons are not affected, since the phonon mean free path is larger than the electron MFP in a typical TE material.
Phonon scattering is based on the phonon frequency or wavelength. High-frequency (short wavelength) phonons are scattered largely through an alloy mass-mismatch mechanism while low-frequency phonons are more affected by larger length scale disorder such as nanoparticles and interfaces. As phonon wavelengths in semiconductors4 are limited to the range between 0.5 and 10 nm, having a combination of interatomic scale features (alloying) and larger features (nanoparticles) can effectively scatter phonons over a large range from small to long wavelengths. Moreover, neutral barrier nanoparticles would not affect the electrons as much as charged nanoparticles. Mingo et al.129 recently showed that the inclusion of less than 1% of 5 nm size silicate nanoparticles inside SiGe could decrease the lattice thermal conductivity by a factor of 5 without affecting the electrical conductivity. According to their theory, even larger nanoparticles (100 nm) still decrease the thermal conductivity. However, for larger nanoparticles, as was discussed before, the carriers (phonons in this case) would spend a considerable amount of time within nanoparticles and would scatter from other centers inside the nanoparticles. Another important factor ignored in their theory is the charge transfer between nanoparticles and the host matrix, which greatly affects the electrical conductivity.
In our group we have incorporated 0.5% of NiSi2 particles (<100 nm in size) inside a SiGe host sample and we have observed an increase in the thermal conductivity (from 2.7 to 4 W mK−1) and increase in the electrical conductivity (from 9.7 to 15.2 × 104 S m−1). The increase in the electrical conductivity occurs because of the charge transfer from the nanoparticles to the host. Note that these nanoparticles are metallic. The enhanced thermal conductivity partly comes from the enhancement in the electronic κe and partly comes from the fact that the lattice thermal conductivity κL of NiSi2 is much larger than that of SiGe. If we look at the final composite as an average of the individual components, it is not surprising to observe such enhancements. Despite these observations which are in contradiction with calculations in ref. 129, their calculations are very valuable and are still valid for smaller nanoparticle sizes. Knowing the limitations of such theories is important in designing nanoscale TE materials. After realizing this, we tried another set of experiments. This time we added 1% of small nanoparticles of about 5 nm in size inside n-type skutterudites and we were able to successfully reduce the thermal conductivity of the skutterudite nanocomposites at room temperature from 3 W mK−1 to 2 W mK−1 and therefore we were able to enhance ZT by 33%. These results will be published in future.
As was mentioned before, the biggest challenge is to embed the desired nanoparticles with the proper size inside the host matrix. There are two major ways to incorporate nanoparticles inside a host matrix to form a nanostructured material. The first way is to process the ingot and break it up into nanocrystalline pieces and then to press the pieces together with the host nanograins to form a bulk material. There are several difficulties with this approach. The main difficulty is to make a very fine (nanoscale size) powder without forming clusters. Another problem is to preserve the nanoparticles during the pressing process. Most of the time hot pressing is involved, during which nanoparticles can melt and form another phase with the host grains.
The second method to incorporate nanoparticles is to use self-formed inhomogeneities on the nanoscale, driven by phase segregation phenomena. This kind of nanostructuring in bulk materials was discovered first in the AgPbmSbTe2+m (LAST-m)130 system and is an inherent property of this system resulting from the AgSbTe2 reaction with PbTe. The components of the compound are melted together and then the sample is quenched and shows a single phase X-ray pattern and the phase separation occurs after annealing.131 The main problem of this method is the fact that it cannot be applied to any arbitrary system and limits the choice of the material. Furthermore, one cannot control the volume fraction of nanophases. In the LAST example, only large m values (m > 10) exhibit nanophases and therefore only a large volume fraction of nanophases is possible.132 In a recent work, Biswas et al.133 demonstrated the endotaxially arranged SrTe nanocrystals incorporated in a PbTe host matrix. The SrTe precipitates have a size distribution of 1–15 nm. It was shown that low concentration of such precipitates (<2%) can block the phonons effectively without modifying the hole mobility.
Holes can be used as an alternative to nanoparticles. The advantage is that the band bending is negligible and it might be easier experimentally to make holes compared to embedding nanoparticles. Yang's group recently showed that holey silicon can have a ZT of 0.4 at room temperature which is comparable to that of SiGe.134
B. Modulation doping
Another strategy to increase ZT is to increase the electron mobility via modulation doping. In modulation doping, charge carriers are spatially separated from their parent impurity atoms to reduce the influence of impurity scattering and thereby increase the mobility of the charge carriers by remote doping.135,136Modulation doping has only been used in thin-film structures for electron transport along the film plane. The active layer of the modulation-doped structure usually consists of an undoped channel for the mobile carriers, an undoped spacer layer that separates the ionized dopants from the conducting channel, and a doping layer. The heterointerface is located between the channel and the spacer and separates the two regions energetically. Carriers then travel parallel to the film with much reduced impurity scattering and therefore with an enhanced mobility.
We have recently applied a similar concept to bulk nanocomposite TE materials. In a recent paper we have demonstrated the effectiveness of this approach in the case of TE materials by using two types of nanograins.137 We incorporated dopants only into the minority silicon nanograins. These grains are then mixed with the majority of undoped SiGe host nanograins. Finally, the mixture of these types of grains is pressed to form a bulk material. Due to the band alignment between the grains, the charge carriers spill over from the nanoparticles into the surrounding host matrix, while the ionized dopant atoms remain spatially segregated within the nanoparticles. The key in 3D modulation doping is the close proximity of the interfaces. Interfaces are only separated by an average distance of 20 nm. Given a screening length of 5–10 nm, carriers can flow through the whole host matrix, rather than being confined at the interfaces.
In our demonstrated case,137 we have observed a 40% enhancement in the power factor compared to uniformly alloyed nanocomposites which was a direct result of the enhanced mobility. Fig. 5 shows the concept of the modulation doping and our experimental demonstration of the enhanced power factor.
![Demonstration of enhanced power factor using the modulation-doping technique. Left: power factor of a p-type modulation-doped sample, (Si80Ge20)70(Si100B5)30 (black squares), compared to the uniformly alloyed single-phase nanocomposite sample Si86Ge14B1.5 (red-filled circles) and to the p-type SiGe bulk alloy used in RTGs for space power missions (solid line). Right: schematic view showing the modulation doping scheme. Impurities are incorporated only inside nanoparticles [after ref. 137].](/image/article/2012/EE/c1ee02497c/c1ee02497c-f5.gif) | ||
| Fig. 5 Demonstration of enhanced power factor using the modulation-doping technique. Left: power factor of a p-type modulation-doped sample, (Si80Ge20)70(Si100B5)30 (black squares), compared to the uniformly alloyed single-phase nanocomposite sample Si86Ge14B1.5 (red-filled circles) and to the p-type SiGe bulk alloy used in RTGs for space power missions (solid line). Right: schematic view showing the modulation doping scheme. Impurities are incorporated only inside nanoparticles [after ref. 137]. | ||
There is a lot of room to advance modulation-doping strategy in nanocomposites. Here we would like to discuss some possible ways. The first observation in our experiment was the increase of thermal conductivity. A part of the enhanced thermal conductivity is inevitable and comes from the enhanced electrical conductivity. However, a major part comes from the enhanced lattice thermal conductivity. This part can be prevented, for example, by using low thermal conductivity materials as nanoparticles or by alloying the nanoparticles. Another problem is the fact that a considerable amount of impurities are actually precipitated to the interfaces and therefore, are not really far from the carriers. Ideally we would like to confine all the impurities within the core of the nanoparticles so that the carriers inside the host do not see them. If one can coat the nanoparticles with another layer of undoped material to serve as the spacer layer, much larger mobility enhancements can be achieved. The spacer should have its conduction band lying below the nanoparticle conduction band and above the host conduction band, so that electrons fall from the nanoparticle to the spacer and then to the host matrix.
In a way, modulation doping in nanocomposites is similar to incorporating ionized nanoparticles inside a host matrix. The question of whether or not ionized nanoparticles are better than ionized impurities has been around for a while. It has been shown that uniform sized nanoparticles scatter electrons less than their equivalent ionized impurities and therefore improve the carrier mobility significantly especially at low temperatures.138 We here would like to emphasize that modulation doping is most beneficial at low temperatures for two reasons. First, at high temperatures, electronic transport mainly suffers from phonon scattering rather than impurity scattering. Second, at low temperatures, most of the impurities are not ionized. On the other hand, due to the intrinsic band offset between the host and the nanoparticles in the modulation scheme, high carrier concentrations can be reached even at low temperatures.
C. Doping optimization
Enhancing the TE power factor through doping optimization seems to be the most trivial and possibly the oldest known method. It is well known that the TE power factor has an optimum versus the carrier concentration. Despite this, in few recent papers, enhanced power factors were achieved in known thermoelectric materials only by doping optimization.Bubnova et al.139 were able to control the doping level of conducting polymers by controlling the oxidation level and achieved a ZT of 0.25 at room temperature which is very large for polymers.
For a single valley band structure, there is only one optimum point for a TE material in the power factor versuscarrier concentration. Multiple valleys introduce more peaks. Multiple degenerate valleys can increase the density of states and therefore the Seebeck coefficient. At the same time, each valley can have a small effective mass and therefore large carrier mobility. Recently the Snyder group126 was able to heavily dope lead telluride and use the twelve-fold degeneracy of the Σ valence band to increase the figure of merit of PbTe1−xSex to 1.8 at 850 K.
III. Device physics
The thermoelectric figure of merit has been increased in the past decade to values higher than 1.5. At this stage, it is important to focus on device design and testing in parallel to material development. First of all, making a good device can confirm achieved high ZT values. Second, there are lots of parasitic losses in the device that lower the efficiency below predicted values based on the materials efficiency. It is a challenge to study such parasitic losses and to reduce them as much as possible. In an ideal world, the thermoelectrics community should ask what the device efficiency is (under what temperature difference) rather than its ZT values, similar to the PV community. Certainly, reporting device efficiency requires solving more challenges related to contacts and device making.A TE power generator device consists of p and n legs which are connected electrically in series and thermally in parallel. The p and n legs are joined by a metal interconnect and the series of legs are placed in between a heat source and a heat sink. The maximum efficiency of the device (ηmax) can be obtained when the external load resistance is matched with the device resistance and can be written as:140
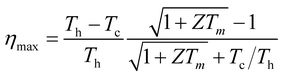 | (1) |
A closer look into the conditions and assumptions under which eqn (1) is derived reveals that there are more factors in determining the device efficiency than only materials performance. In driving eqn (1), electrical and thermal resistances of the contacts and electrodes are neglected and constant ZT values are assumed. For example a ZT of 2 would result in 30% efficiency when the heat sink is at room temperature and the heat source is at 1300 K (see Fig. 6). However, to achieve 30% efficiency, one needs both a p-type and an n-type material, each with an average ZT of 2 (and not a peak ZT of 2) over 1000 degrees of temperature range.
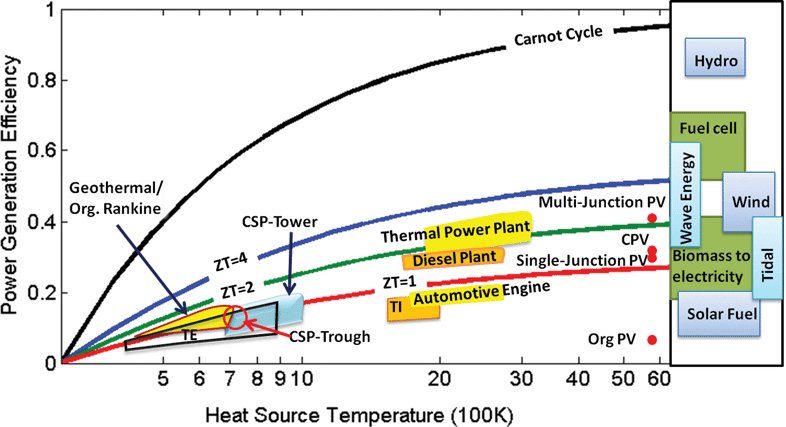 | ||
| Fig. 6 Power generation efficiency versus temperature of the hot side, plotted for different energy conversion technologies. The cold side is assumed to be at room temperature. The efficiency range of some of the other renewable energy technologies is marked in a bar on the right-hand side of the graph. In this graph PV is photovoltaic; CSP denotes concentrated solar power; and Org, TE and TI denote organic, thermoelectric and thermionic devices, respectively. | ||
Making good contacts to TE devices is challenging for several reasons. First, the device operates under a large temperature difference which leads to thermal mechanical stress, diffusion and the chemical reaction of materials at their interfaces. Second, TE materials have high electrical conductivity and hence very low electrical contact resistances are required between the materials and the electrodes. These problems limit the choice of the electrode materials. The electrodes should have high electrical and thermal conductivities relative to the TE material; their coefficient of thermal expansion should match with that of the TE material and they should be chemically stable over the life time of the module and do not interact with the TE materials. In fact, often the electrodes also include diffusion barriers to prevent the diffusion of certain electrode materials into the thermoelectric materials. Because thermoelectric devices operate under large currents and a large temperature gradient, both electrical and thermal migration could occur. These phenomena have not been studied in detail.141–143
Assembling individual legs into a thermoelectric module represents another challenge. Typical module geometry is made of many p–n pairs placed in parallel to each other. How to assemble many pairs of legs into one module without using solders is a challenge and may require different solutions for different materials. Thermal expansion of all pairs further aggregates the stress accumulation. Innovative device designs, such as placing p–n pairs parallel to each other (Lon-Bell device144), reduce the thermal stress.
Device testing is another challenge facing the thermoelectrics community. Unlike PV cell efficiency measurements, thermoelectric device efficiency measurements require quantifying the heat input to the hot side and the heat removed from the cold side, and quantifying the electrical output, which is maximum at matched load. For constant properties, the maximum efficiency obtained from eqn (1) occurs when the external load is matched with the internal resistance by a factor of 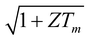 . In reality, this load matching is best achieved by using a programmable current source and runs in reverse to the current direction driven by the temperature gradient. The most difficult part of the efficiency measurements is in determining precisely the heat input or heat removed, as the electrodes and thermocouples can all lead to additional thermal leakage. Careful calibration of the various heat losses is essential for an accurate determination of the efficiency. The thermoelectrics community presently lacks a standard in efficiency measurements. This can be contrasted with the PV field, where efficiency is the stick to gauge success, rather than material parameters.
. In reality, this load matching is best achieved by using a programmable current source and runs in reverse to the current direction driven by the temperature gradient. The most difficult part of the efficiency measurements is in determining precisely the heat input or heat removed, as the electrodes and thermocouples can all lead to additional thermal leakage. Careful calibration of the various heat losses is essential for an accurate determination of the efficiency. The thermoelectrics community presently lacks a standard in efficiency measurements. This can be contrasted with the PV field, where efficiency is the stick to gauge success, rather than material parameters.
The field of thermoelectrics needs more research at the device level, from diffusion barriers to contacts, to assembly of modules. So far, the contacts used in TE devices are mostly trial-and-error based. Systematic studies on contact making for TE device applications can have a large impact on the integration of good thermoelectric materials in thermoelectric devices.
IV. Applications
Fig. 6 compares the efficiency of thermoelectric power generators with other types of energy conversion technologies. Although there is no agreed theoretical limit on ZT, it is generally recognized that progress in ZT values is slow, and one should not wait for ZT increase before committing to practical applications. In fact, with a ZT of 1 and depending on temperature differences, thermoelectric devices can have efficiency comparable to several other renewable technologies including some single junction PV cells. In addition, since currently over 90% of our energy supply is used as heat and nearly 60% of the energy input to our society is wasted as heat, there are many such available heat sources that are essentially free. The key is to design systems with competitive electricity cost, i.e., at the $ per W level, not necessarily efficiency. The fact that the most profitable PV company—First Solar, Inc.—is not based on the highest efficiency provides another example that it is $ per W that is most important for energy technology.Currently, prevailing applications of thermoelectric devices are in the cooling area, such as small and mobile refrigerators,145 cooled car seats,146 temperature regulators of semiconductor lasers,147 and medical148 and scientific instruments.149
For power generation, thermoelectric generators have demonstrated their use in space applications. Terrestrial applications are fewer, such as remote power along oil pipelines and body temperature powered watches. A major driver for application now is in vehicle waste heat recovery, because automobiles have efficiencies only around 20%. About 1/3 of the heat is wasted through the exhaust pipe and another 1/3 is wasted through the radiator. Among the two major heat sources in automobiles, the exhaust pipe has the higher temperature and is more suitable for thermoelectrics. All major auto-makers have programs on thermoelectric waste heat recovery for conversion to electricity, driven by legislation on CO2 emission requirements for future vehicles. For example, the European Parliament and of the Council of 23 April 2009 have set emission performance standards for new passenger cars as part of the Community's integrated approach to reduce CO2 emissions from light-duty vehicles.150 From 2012, if the average CO2 emissions of a manufacturer's fleet exceed its limit value, the manufacturer must pay an excess emissions premium for each car registered. This premium amounts to €5 for the first g km−1 by which emission exceeds requirements, €15 for the second g km−1, €25 for the third g km−1, and €95 for each subsequent g km−1. From 2019, the first g km−1 will already have a €95 penalty cost. If thermoelectric systems can improve the overall system efficiency by 1%, their technology effectively leads to 5% fuel saving. Each kilogram of fuel saving reduces CO2 emissions by 3.16 kg.
It is fair to say that vehicle applications are policy driven and are the most demanding of all applications. Thermoelectrics is attractive because it is a solid state technology. However, vehicle applications are also arguably the most challenging because of varying driving conditions, the size and weight limit requirements, etc. There are many other heat sources that thermoelectrics can use, from industrial waste heat to co-generations of heat and electricity.151 Probably the best application would be in cases where a heat source is available 24 hours a day, 7 days a week. These kinds of sources can provide constant heat flux for the TE modules. Competition in this case comes from other technologies such as the Rankine cycle. However, Rankine cycles are mechanical systems that use fluids (either water for higher temperatures of around 500 °C or organic fluids for lower operating temperatures of 70–90 °C). Such large fluid systems are not desirable for many applications. System analysis, considering heat sources and heat sink requirements, is needed to identify promising applications.
An interesting recent application of thermoelectric devices is in the solar thermoelectric generators (STEGs). The idea is to concentrate solar energy to create heat that a TEG turns into electricity.152 The maximum efficiency of STEGs is a product of the opto-thermal efficiency and the device efficiency and STEGs have an optimum efficiency versus hot-side temperature.153 Experimentally, Kraemer et al.154 demonstrated a flat-panel STEG with a high thermal concentration which achieved a peak efficiency of 4.6% under AM1.5G (1 kW m−2) conditions. The efficiency is 7–8 times higher than the previously reported best value for a flat-panel STEG. To create a large temperature gradient along the TE module, instead of using an optical concentrator which is costly, a highly solar-absorbing surface is used which converts the solar radiation into heat and thermally concentrates it onto the TE elements by means of lateral heat conduction. Such flat-panel STEGs do not require tracking and can be a cost effective technology to convert solar energy into electricity. Vacuum-based STEG technology is compatible with widely used evacuated solar hot-water collector tubes, indicating the potential of STEGs for the co-generation of electricity and hot water, thus leading to improved system efficiency and reduced cost. A schematic of the STEG device is shown in Fig. 7.
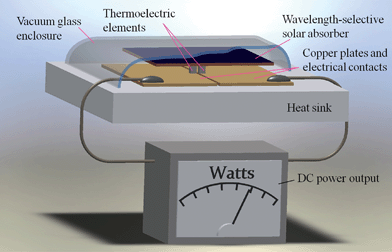 | ||
| Fig. 7 Illustration of a STEG cell made from a pair of p- and n-type thermoelectric elements, a flat-panel selective absorber that also acts as a thermal concentrator, and two bottom electrodes that serve as heat spreaders and radiation shields. The device is surrounded by a glass enclosure maintaining an evacuated environment. | ||
We want to emphasize that the cost of thermoelectric energy systems depends not only on the module cost, for which the materials cost is a major factor, but also the system cost.155 In the case of the STEG example given above, thermoelectric materials cost can be controlled down to $0.1–0.2 per W. Heat exchangers at the hot and the cold side can be a major part of the cost. It is thus important to evaluate cost at the system level. Some of the literature has emphasized that thermoelectric devices can require high heat flux. While such high heat flux is useful in some applications, it is not suitable for most waste heat, or renewable heat, where energy conversion intrinsically involves lower heat flux inputs. A large heat flux mismatch can lead to additional temperature drops outside the thermoelectric devices and thereby reduce system efficiency.
Every year the energy commissions assess the performance, power output, instant cost and levelized cost of different renewable energy technologies and compare them with other energy conversion technologies.156,157 Thermoelectrics though is not considered in these evaluations, mainly because they are not widely commercialized. It is up to the TE community to take a closer look at the cost analysis and device performance of TE modules. The capital cost of the TE modules (2–5 $ per W) and their life time (15–20 years) are not far behind other technologies. However, we have a lack of information about the levelized cost (constant cost per unit of electric power generation). An accurate evaluation of such a cost will help the TE community to make a better decision on the potential of thermoelectrics for power generation applications.
V. Conclusions
In this review, we updated the last two-year advances of the thermoelectric field in terms of understanding electron and phonon transport within nanostructured TE materials. While phonon transport inside bulk materials is much better understood using first-principles-based methods, electron transport has not advanced as much. In terms of transport in nanostructures, still there is a lack of solid experimental characterization techniques to identify the structure and shape of individual interfaces, as well as carrier transmissivity across the interface. On the theory side, we need more advanced theories and computational techniques to identify transmissivity through a single interface as well as transport through multiple interfaces when they are closer than the carrier MFP and when the nanoparticles are larger than the carrier MFP.We have reviewed a few strategies that have in the past demonstrated improved TE materials efficiencies. The discussed strategies include energy filtering and resonant states to improve the Seebeck coefficient, nanoparticles in alloys used to decrease the thermal conductivity without modifying the electrical conductivity, and modulation doping to enhance the mobility.
With increased ZT values, the thermoelectrics community needs to start standardization of their characterization techniques in order to confirm reliable high ZT values and to develop practical systems for real world applications. We emphasize that the thermoelectrics community should think more about efficiency and dollar per watt rather than ZT. Even with current ZT values, there are good opportunities to develop commercial applications.
Acknowledgements
We would like to thank Daniel Kraemer for providing the STEG graph, Giri Joshi for providing NiSi2 and Half-Heusler data and Jivtesh Garg, Tengfei Luo and Junichiro Shiomi for providing the thermal conductivity data. This article is partially based upon work supported as part of the MIT S3TEC, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-FG02-09ER46577 for basic research in thermoelectric transport and materials, and solar thermoelectric prototypes; and by Bosch within the MIT Energy Initiative for waste heat recovery application. Work on PbTe is funded by DOE Grant No. DE-FG02-08ER46516.Notes and references
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466 CAS.
- A. F. Ioffe, Thermoelements and Thermoelectric Cooling, Infosearch Limited, London, 1957 Search PubMed.
- M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J. P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043 CrossRef CAS.
- J. Baxter, Z. X. Bian, G. Chen, D. Danielson, M. S. Dresselhaus, A. G. Fedorov, T. S. Fisher, C. W. Jones, E. Maginn, U. Kortshagen, A. Manthiram, A. Nozik, D. R. Rolison, T. Sands, L. Shi, D. Sholl and Y. Y. Wu, Energy Environ. Sci., 2009, 2, 559 CAS.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616 CrossRef CAS.
- Y. C. Lan, A. J. Minnich, G. Chen and Z. F. Ren, Adv. Funct. Mater., 2010, 20, 357 CrossRef CAS.
- C. J. Vineis, A. Shakouri, A. Majumdar and M. G. Kanatzidis, Adv. Mater., 2010, 22, 3970 CrossRef CAS.
- A. Shakouri and M. Zebarjadi, in Thermal Nanosystems and Nanomaterials, ed. S. Volz, Springer, Berlin/Heidelberg, 2009, pp. 225–244 Search PubMed.
- A. I. Hochbaum and P. D. Yang, Chem. Rev., 2010, 110, 527 CrossRef CAS.
- D. L. Medlin and G. J. Snyder, Curr. Opin. Colloid Interface Sci., 2009, 14, 226 CrossRef CAS.
- E. Pop, Nano Res., 2010, 3, 147 CrossRef CAS.
- J. Callaway, Phys. Rev., 1959, 113, 1046 CrossRef CAS.
- D. A. Broido, M. Malorny, G. Birner, N. Mingo and D. A. Stewart, Appl. Phys. Lett., 2007, 91, 231922 CrossRef.
- A. Ward and D. A. Broido, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085205 CrossRef.
- A. Ward, D. A. Broido, D. A. Stewart and G. Deinzer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125203 CrossRef.
- J. Garg, N. Bonini, B. Kozinsky and N. Marzari, Phys. Rev. Lett., 2011, 106, 045901 CrossRef.
- N. Koker, Phys. Rev. Lett., 2009, 103, 125902 CrossRef.
- B. Huang and M. Kaviany, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125209 CrossRef.
- B. Huang and M. Kaviany, Acta Mater., 2010, 58, 4516 CrossRef CAS.
- K. Esfarjani and H. T. Stokes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144112 CrossRef.
- M. S. Green, J. Chem. Phys., 1954, 22, 398 CrossRef CAS.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570 CrossRef.
- J. Shiomi, K. Esfarjani and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104302 CrossRef.
- A. S. Henry and G. Chen, J. Comput. Theor. Nanosci., 2008, 5, 141 CAS.
- A. McGaughey and M. Kaviany, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 094303 CrossRef.
- K. Esfarjani, G. Chen and H. T. Stokes, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085204 CrossRef.
- T. Shiga, J. Shiomi, K. Esfarjani, O. Delaire and G. Chen, unpublished.
- T. Luo, J. Garg, K. Esfarjani and G. Chen, unpublished.
- C. Dames and G. Chen, Thermal Conductivity of Nanostructured Thermoelectric Materials, ed. M. Rowe, CRC Handbook, Taylor and Francis, Boca Raton, 2006 Search PubMed.
- O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M. H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden and B. C. Sales, Nat. Mater., 2011, 10, 614 CrossRef CAS.
- Y. K. Koh and D. G. Cahill, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075207 CrossRef.
- A. J. Minnich, J. A. Johnson, A. J. Schmidt, K. Esfarjani, M. S. Dresselhaus, K. A. Nelson and G. Chen, Phys. Rev. Lett., 2011, 107, 095901 CrossRef CAS.
- G. Chen, J. Heat Transfer, 1996, 118, 539 CrossRef CAS.
- M. E. Siemens, Q. Li, R. Yang, K. A. Nelson, E. H. Anderson, M. M. Murnane and H. C. Kapteyn, Nat. Mater., 2010, 9, 26 CrossRef CAS.
- A. Minnich and G. Chen, Proceedings of the 8th ASME/JSME Thermal Engineering Joint Conference, Honolulu, HI, March 2011 Search PubMed.
- J. A. Johnson, A. A. Maznev, A. Minnich, K. Collins, G. Chen, J. Cuffe, C. M. S. Torres and K. A. Nelson, Symposium Bb, MRS, San Francisco, 2011 Search PubMed.
- D. G. Cahill, K. Goodson and A. Majumdar, J. Heat Transfer, 2002, 124, 223 CrossRef CAS.
- G. P. Srivastava, The Physics of Phonons, Taylor and Francis Group, New York, 1990 Search PubMed.
- E. T. Swartz and R. O. Pohl, Rev. Mod. Phys., 1989, 61, 605 CrossRef.
- G. Chen, Nanoscale Energy Transfer and Conversion, Oxford University Press, 2005 Search PubMed.
- K. C. Collins, S. Chen and G. Chen, Appl. Phys. Lett., 2010, 97, 083102 CrossRef.
- E. S. Landry and A. J. H. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165304 CrossRef.
- L. Sun and J. Y. Murthy, J. Heat Transfer, 2010, 132, 102403 CrossRef.
- X. P. Huang, X. L. Huai, S. Q. Liang and X. W. Wang, J. Phys. D: Appl. Phys., 2009, 42, 095416 CrossRef.
- M. Hu, P. Keblinski and P. K. Schelling, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104305 CrossRef.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, UK, 1995 Search PubMed.
- E. N. Economou, Green's Functions in Quantum Physics, Springer Verlag, 3rd edn, 2006 Search PubMed.
- D. P. Sellan, E. S. Landry, J. E. Turney, A. J. H. McGaughey and C. H. Amon, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214305 CrossRef.
- Q. Hao, G. Chen and M. S. Jeng, J. Appl. Phys., 2009, 106, 114321 CrossRef.
- M. S. Jeng, R. G. Yang, D. Song and G. Chen, J. Heat Transfer, 2008, 130, 042410 CrossRef.
- S. V. J. Narumanchi, J. Y. Murthy and C. H. Amon, J. Heat Transfer, 2004, 126, 946–955 CrossRef CAS.
- Z. Huang, T. Fisher and J. Murthy, J. Appl. Phys., 2011, 109, 074305 CrossRef.
- Y. Xu, X. Chen, J. S. Wang, B. L. Gu and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195425 CrossRef.
- N. Mingo, in Thermal Nanosystems and Nanomaterials, ed. S. Volz, Springer, 2009, pp. 63–93 Search PubMed.
- N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 125402 CrossRef.
- J. S. Wang, J. Wang and N. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 033408 CrossRef.
- K. H. Yoo and A. C. Anderson, J. Low Temp. Phys., 1986, 63, 269–286 CrossRef CAS.
- A. Majumdar and P. Reddy, Appl. Phys. Lett., 2004, 84, 4768 CrossRef CAS.
- G. D. Mahan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 075408 CrossRef.
- M. V. Simkin and G. D. Mahan, Phys. Rev. Lett., 2000, 84, 927 CrossRef CAS.
- R. Venkatasubramanian, Phys. Rev. B: Condens. Matter, 2000, 61, 3091–3097 CrossRef CAS.
- B. Yang and G. Chen, Phys. Rev. B: Condens. Matter, 2003, 67, 195311 CrossRef.
- G. Chen, Phys. Rev. B: Condens. Matter, 1998, 57, 14958–14973 CrossRef CAS.
- L. Onsager, Phys. Rev., 1931, 37, 405 CrossRef CAS.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Brooks/Cole, Belmont, USA, 1976, ch. 13 Search PubMed.
- M. R. Peterson and B. S. Shastry, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195105 CrossRef.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67 CrossRef CAS.
- D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter, 1990, 41, 7868 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter, 1991, 44, 943 CrossRef CAS.
- A. Georges, G. Kotliar, W. Krauth and M. Rozenberg, Rev. Mod. Phys., 1996, 68, 13 CrossRef CAS.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef CAS; L. Hedin and S. Lundqvist, Solid State Phys., 1970, 23, 1 CrossRef; M. S. Hybertsen and S. G. Louie, Phys. Rev. B, 1986, 34, 5390 CrossRef.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter, 1995, 52, R5467–R5470 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- M. I. Katsnelson and A. I. Lichtenstein, Eur. Phys. J. B, 2002, 30, 9–15 CrossRef CAS.
- F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108 CrossRef.
- J. Sjakste, V. Tyuterev and N. Vast, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 235216 CrossRef.
- J. Sjakste, N. Vast and V. Tyuterev, Phys. Rev. Lett., 2007, 99, 236405 CrossRef.
- V. Tyuterev, J. Sjakste and N. Vast, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245212 CrossRef.
- F. Murphy-Armando and S. Fahy, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035202 CrossRef.
- C. H. Park, F. Giustino, C. D. Spataru, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2009, 102, 076803 CrossRef.
- A. Leonardo, I. Y. Sklyadneva, V. M. Silkin, P. M. Echenique and E. V. Chulkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 035404 CrossRef.
- O. Restrepo, K. Varga and S. Pantelides, Appl. Phys. Lett., 2009, 94, 212103 CrossRef.
- Z. Wang, S. Wang, S. Obukhov, N. Vast, J. Sjakste, V. Tyuterev and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205208 CrossRef.
- D. J. Howarth and E. H. Sondheimer, Proc. R. Soc. London, Ser. A, 1953, 19341990 Search PubMed.
- D. L. Rode, Phys. Rev. B: Solid State, 1970, 2, 1012 CrossRef.
- A. Shakouri, E. Y. Lee, D. L. Smith, V. Narayanamurti and J. E. Bowers, Microscale Thermophys. Eng., 1998, 2, 37 CrossRef CAS.
- M. Zebarjadi, A. Shakouri and K. Esfarjani, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195331 CrossRef.
- Z. X. Bian and A. Shakouri, Appl. Phys. Lett., 2006, 88, 012102 CrossRef.
- M. Zebarjadi, K. Esfarjani and A. Shakouri, Appl. Phys. Lett., 2007, 91, 122104 CrossRef.
- A. J. Minnich, H. Lee, X. W. Wang, G. Joshi, M. S. Dresselhaus, Z. F. Ren, G. Chen and D. Vashaee, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155327 CrossRef.
- J. Zhou, X. B. Li, G. Chen and R. G. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115308 CrossRef.
- C. Bera, M. Soulier, C. Navone, G. Roux, J. Simon, S. Volz and N. Mingo, J. Appl. Phys., 2010, 108, 124306 CrossRef.
- S. Ahmad and S. D. Mahanti, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165203 CrossRef.
- S. V. Faleev and F. Leonard, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214304 CrossRef.
- M. Zebarjadi, K. Esfarjani, A. Shakouri, J. Bahk, Z. X. Bian, G. Zeng, J. E. Bowers, H. Lu, J. M. O. Zide and A. C. Gossard, Appl. Phys. Lett., 2009, 94, 202105 CrossRef.
- M. Zebarjadi, K. Esfarjani, Z. X. Bian and A. Shakouri, Nano Lett., 2011, 11, 225 CrossRef CAS.
- S. Datta, Quantum Transport: Atom to Transistor, Cambridge Univ. Press, UK, 2005 Search PubMed.
- S. Wang and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115316 CrossRef.
- D. Vashaee and A. Shakouri, J. Appl. Phys., 2004, 95, 1233 CrossRef CAS.
- A. Popescu, L. M. Woods, J. Martin and G. S. Nolas, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205302 CrossRef.
- H. Wang and D. R. Johnson, DOE 2011Thermoelectric Application Workshop, San Diego, CA, 2011 Search PubMed; H. Böttner, L. Chen, R. Funahashi, F. Harris, H. W. Lee, J. Lo, A. Mayolet, T. Tritt and H. Wang, The 30th International Conference on Thermoelectrics, W12.1, Traverse City, Michigan, USA, July 17–21, 2011 Search PubMed.
- A. Muto, PhD thesis, Massachusetts Institute of Technology, Dept. of Mechanical Engineering, 2011.
- A. Muto, J. Yang, Z. F. Ren and G. Chen, unpublished.
- X. Yan, B. Poudel, Y. Ma, W. S. Liu, G. Joshi, H. Wang, Y. C. Lan, D. Z. Wang, G. Chen and Z. F. Ren, Nano Lett., 2010, 10, 3373 CrossRef CAS.
- X. W. Wang, H. Lee, Y. C. Lan, G. H. Zhu, G. Joshi, D. Z. Wang, J. Yang, A. Muto, M. Y. Tang, J. Klatsky, S. Song, M. S. Dresselhaus, G. Chen and Z. F. Ren, Appl. Phys. Lett., 2008, 93, 193121 CrossRef.
- A. D. Lalonde, Y. Pei and G. J. Snyder, Energy Environ. Sci., 2011, 4, 2090 CAS.
- J. Androulakis, I. Todorov, J. He, D. Y. Chung, V. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2011, 133, 10920 CrossRef CAS.
- X. Shi, J. Yang, J. R. Salvador, M. F. Chi, J. Y. Cho, H. Wang, S. Q. Bai, J. H. Yang, W. Q. Zhang and L. D. Chen, J. Am. Chem. Soc., 2011, 133, 7837 CrossRef CAS.
- G. Joshi, X. Yan, H. Wang, W. Liu, G. Chen and Z. F. Ren, Adv. Energy Mater., 2011, 1, 643–647 CrossRef CAS.
- B. Poudel, Q. Hao, Y. Ma, Y. C. Lan, A. Minnich, B. Yu, X. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Y. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, Science, 2008, 320, 634 CrossRef CAS.
- G. Joshi, H. Lee, Y. Lan, X. Wang, G. Zhu, D. Wang, R. W. Gould, D. C. Cuff, M. Y. Tang, M. S. Dresselhaus, G. Chen and Z. F. Ren, Nano Lett., 2008, 8, 4670 CrossRef CAS.
- H. Wang, Y. Z. Pei, A. D. LaLonde and G. J. Snyder, Adv. Mater., 2011, 23, 1366 CrossRef CAS.
- P. F. Qiu, J. Yang, R. H. Liu, X. Shi, X. Y. Huang, G. J. Snyder, W. Zhang and L. D. Chen, J. Appl. Phys., 2011, 109, 063713 CrossRef.
- X. Yan, G. Joshi, W. S. Liu, Y. C. Lan, H. Wang, S. Lee, J. W. Simonson, S. J. Poon, T. M. Tritt, G. Chen and Z. F. Ren, Nano Lett., 2011, 11, 556 CrossRef CAS.
- B. Y. Moizhes and V. A. Nemchinsky, in Proc. for the 11th Int. Conf. on Thermoelectrics, University of Texas, Arlington, TX, 1992 Search PubMed.
- A. Shakouri and J. E. Bowers, Appl. Phys. Lett., 1997, 71, 1234 CrossRef CAS.
- G. D. Mahan, Semicond. Semimetals, 2001, 71, 157 CrossRef CAS.
- J. M. O. Zide, D. Vashaee, Z. X. Bian, G. Zeng, J. E. Bowers, A. Shakouri and A. C. Gossard, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 205335 CrossRef.
- N. F. Mott, Adv. Phys., 1967, 16, 49 CrossRef CAS.
- D. K. Ko, Y. Kang and C. B. Murray, Nano Lett., 2011, 11, 2841 CrossRef CAS.
- B. Paul, V. A. Kumar and P. Banerji, J. Appl. Phys., 2010, 108, 064322 CrossRef.
- J. P. Heremans, C. M. Thrush and D. T. Morelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 115334 CrossRef.
- J. P. Heremans, V. Jovovice, E. S. Toberer, A. Saramat, K. Kurasaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554 CrossRef CAS.
- Y. Pei, X. Shi, A. Lalonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66 CrossRef CAS.
- L. I. Schiff, Quantum Mechanics, McGraw-Hill, New York, 1949 Search PubMed.
- J. M. Ziman, Electrons and Phonons, Oxford University Press, New York, 2001 Search PubMed.
- N. Mingo, D. Hauser, N. P. Kobayashi, M. Plissonnier and A. Shakouri, Nano Lett., 2009, 9, 711 CrossRef CAS.
- K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Hogan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2010, 303, 818–821 CrossRef.
- M. G. Kanatzidis, Chem. Mater., 2010, 22, 648–659 CrossRef CAS.
- Y. Z. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin, L. Douglas and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241–249 CrossRef CAS.
- K. Biswas, J. He, Q. Zhang, G. Wang, C. Uher, V. P. Dravid and M. G. Kanatzidis, Nat. Chem., 2011, 3, 160 CrossRef CAS.
- J. Tang, H. T. Wang, D. H. Lee, M. Fardy, Z. Huo, T. P. Russell and P. Yang, Nano Lett., 2010, 10, 4279 CrossRef CAS.
- R. Dingle, H. L. Stormer, A. C. Gossard and W. Wiegmann, Appl. Phys. Lett., 1978, 33, 665 CrossRef CAS.
- H. Daembkes, Modulation-Doped Field-Effect Transistors: Principles, Design, and Technology, IEEE Press, New York, 2nd edn, 1991 Search PubMed.
- M. Zebarjadi, G. Joshi, G. H. Zhu, B. Yu, A. Minnich, Y. C. Lan, X. W. Wang, M. S. Dresselhaus, Z. F. Ren and G. Chen, Nano Lett., 2011, 11, 2225 CrossRef CAS.
- M. Zebarjadi, K. Esfarjani, Z. X. Bian and A. Shakouri, Nano Lett., 2011, 11, 225 CrossRef CAS.
- O. Bubnova, Z. U. Khan, A. Malti, S. Braun, M. Fahlman, M. Berggren and X. Crispin, Nat. Mater., 2011, 10, 429 CrossRef CAS.
- G. S. Nolas, J. Sharp and H. Goldsmid, Thermoelectrics: Basic Principles and New Materials Developments, Springer, New York, 2001 Search PubMed.
- J. P. Fleurial, A. Borshchevsky, M. A. Ryan, W. Phillips, E. Kolawa, T. Kacisch and R. Ewell, XVI ICT '97. Proceedings ICT'97. 16th International Conference on Thermoelectrics (Cat. No.97TH8291), 1997, 641–645 CrossRef CAS.
- Y. C. Lan, D. Z. Wang, G. Chen and Z. F. Ren, Appl. Phys. Lett., 2008, 92, 101910 CrossRef.
- W. Shin, N. Murayama, K. Ikeda, S. Sago and I. Terasaki, J. Ceram. Soc. Jpn., 2002, 110, 727 CrossRef CAS.
- L. E. Bell, Science, 2008, 321, 1457 CrossRef CAS.
- http://www.koolatron.com/ .
- http://amerigon.com/; http://www.huimao.com/.
- http://www.marlow.com/;http://www.thorlabs.com/;http://www.blueskyresearch.com/.
- http://www.thermotekusa.com/; http://www.customchill.com/.
- http://www.thermo-electric.nl/ .
- http://www.europarl.europa.eu/oeil/file.jsp%3Fid%20%3D%205582632 .
- C. B. Vining, Nat. Mater., 2009, 8, 83 CrossRef CAS.
- G. W. Crabtree and N. S. Lewis, Phys. Today, 2007, 60, 37–42 CrossRef CAS.
- G. Chen, J. Appl. Phys., 2011, 109, 104908 CrossRef.
- D. Kraemer, B. Poudel, H. P. Feng, J. C. Caylor, B. Yu, X. Yan, Y. Ma, X. W. Wang, D. Z. Wang, A. Muto, K. McEnaney, M. Chiesa, Z. F. Ren and G. Chen, Nat. Mater., 2011, 10, 532–538 CrossRef CAS.
- K. Yazawa and A. Shakouri, Environ. Sci. Technol., 2011, 45, 7548–7553 CAS.
- California Energy Commission, CEC-200-2009-017-SD, August 2009.
- Intergovernmental Panel on Climate Change, Special Report Renewable Energy sources (SRREN), IPCC, 2011 Search PubMed.
| This journal is © The Royal Society of Chemistry 2012 |
